Spin Many quantum experiments are done with photon

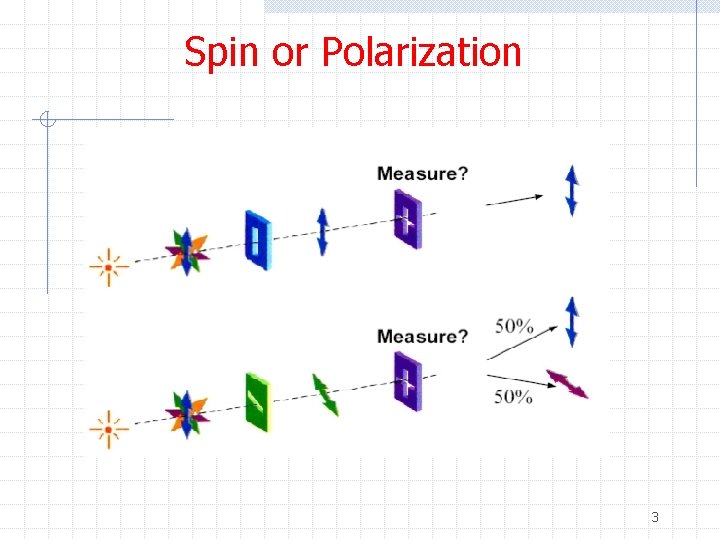
Spin Ø Many quantum experiments are done with photon polarization instead of electron spin Ø Here is the correspondence between the two Ø And the measurement probabilities are the same 1

Spin Ø From our study of spin and Stern-Gerlach experiments we know we must choose a direction (basis) to measure Sz for electrons or linear polarization for photons 2

Spin or Polarization 3

Quantum Cryptography ØHow does the left side of the room pass a note to the right side of the room without me learning the contents of the message? ØThe only mathematically proven way to transmit a message is to use a one-time pad n This requires a key the same length as the message and can be used only once 4

Quantum Cryptography ØNote, the figures on the next few slides were take from a talk on quantum cryptography by Vadim Makarov from NTNU in Norway 5

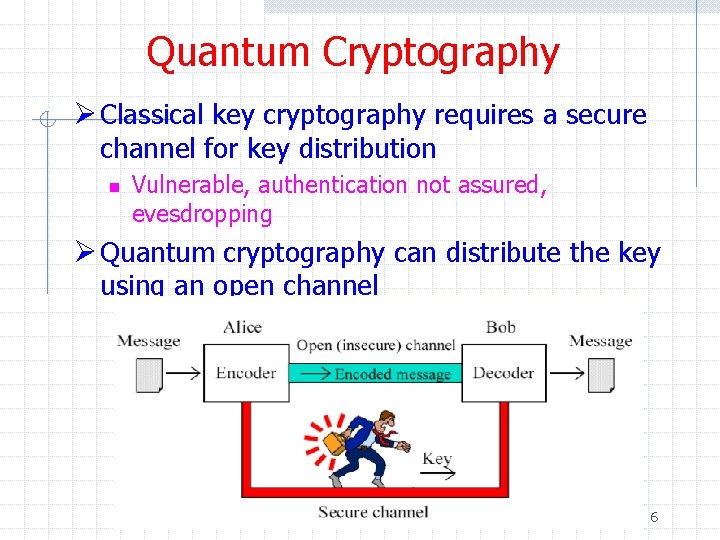
Quantum Cryptography Ø Classical key cryptography requires a secure channel for key distribution n Vulnerable, authentication not assured, evesdropping Ø Quantum cryptography can distribute the key using an open channel 6

Quantum Cyptography Ø In addition, a message transmitted classically can be passively monitored Ø A message transmitted quantum mechanically 7

Quantum Cryptography 8

Quantum Cryptography Ø Alice generates a random key Ø Alice generates a random set of analyzers Ø Alice sends the results to Bob Ø Bob generates a random set of analyzers Ø Alice and Bob publicly exchange what analyzers were used (sifting) Ø Alice and Bob check whether randomly selected entries agree Ø The remaining results are kept as a key 9

Quantum Cryptography 10

Quantum Cryptography Ø Here is Alice 11

Quantum Cryptography Ø Here is Bob 12

Qubit Ø A Qubit (or Qbit) is a quantum system with exactly two degrees of freedom Ø Examples n n Electron with spin up and spin down Photon with horizontal and vertical polarization 13

Entanglement Ø Recall the EPR paradox 14

Entanglement Ø Describes quantum states that have to be referenced to each other even though they are spatially separated Ø Say I can generate electron (or photon) pairs such that they always have opposite spins n n n What is the probability of A measuring up? What is the probability of A measuring down? What is the probability of B measuring up when A measures down? Ø We say the two spins are entangled 15

Quantum Teleportation ØQuantum teleportation transfers a quantum state to an arbitrarily far location using a distributed entangled state and the transmission of classical information ØThe state at A is physically not transferred but an identical copy appears at B 16

Quantum Teleportation Ø Recall that spin can be measured with different SG analyzers (bases) Ø We’ll define 17

Quantum Teleportation Ø Let’s define some operations Ø These don’t destroy the quantum state 18

Quantum Teleportation Ø We want to transfer an arbitrary state from Lab A to Lab B Ø We also start with an entangled state Ø Then the overall state is 19

Quantum Teleportation ØSpin 1 is the unknown spin to be transported ØSpin 2 is the first spin of the entangled pair and is located Lab A ØSpin 3 is the second spin of the entangled pair and is located in Lab B 20

Quantum Teleportation Ø Apply the C-X operation to spins 1 and 2 in Lab A 21

Ø Measure spin 2 in Teleportation the z basis Quantum Ø The probability of getting spin up is n And also 1/2 for getting spin down Ø Let’s say we measure up, then the new state will be 22

Ø Measure spin 1 in Teleportation the x basis Quantum Ø Then the probability of measuring spin right is n And 1/2 for getting spin left Ø Let’s say we measure right, then the new state will be 23

Quantum Teleportation Ø Now call Lab B and tell them the results Ø Lab B responds by Ø Our example is case 3 24

Quantum Teleportation Ø Thus the state of spin 3 in Lab B is Ø Exactly the state we were trying to transmit 25

Quantum Teleportation 26