Spillover effect A study for major capital markets

Spillover effect: A study for major capital markets and Romanian capital market MSc Student: Cristina Belciuganu Coordinator Professor: Moisa Altar July 2008

Topics l l 2 Introduction Methodologies used and results Conclusion References-Annex 12 July 2008 Spillover Effect Study

Topics l l 3 Introduction Methodologies used and results Conclusion References 12 July 2008 Spillover Effect Study

Introduction l l The scope of paper was to study how different capital markets are influencing each other The study is focused on the US market, major European countries and Romania, using the following indexes: – – – l 4 S&P 500, NASDAQ 100 and DJ INDUSTRIALS (US) CAC 40, FTSE 100 and DAX 30 (Europe) BET, Romanian index The period selected for the study was September 1997 – May 2008 12 July 2008 Spillover Effect Study

Introduction l l 5 Instead of considering the risk in term of volatility to risk we reflected in term of extreme losses with low probability of being exceeded This means tail risk and we approach it through 1 day, 95% and 99% Value at Risk measure Our objective is to determine whether this kind of risk, presents spillover effects across the markets. Spillover effects being the influence of one market on others, is examined using the Granger causality, for daily changes of the Va. R series 12 July 2008 Spillover Effect Study

Topics l l 6 Introduction Methodologies used and results Conclusion References-Annex 12 July 2008 Spillover Effect Study

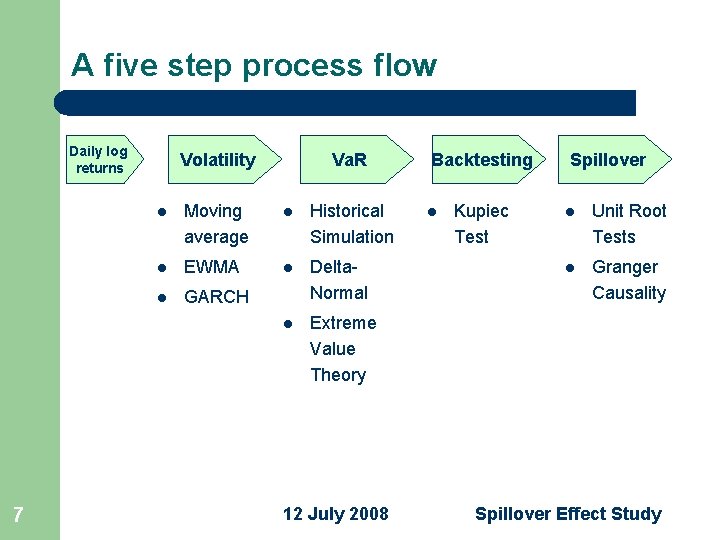
A five step process flow Daily log returns 7 Volatility Va. R l Moving average l Historical Simulation l EWMA l l GARCH Delta. Normal l Extreme Value Theory 12 July 2008 Backtesting l Kupiec Test Spillover l Unit Root Tests l Granger Causality Spillover Effect Study

Standard deviations methods l Moving average – Each day the forecast is updated by adding information from the preceding day and dropping information from (M+1) – 8 We have calculated the moving average using a moving window of 10, 20 and 60 days 12 July 2008 Spillover Effect Study

Standard deviations methods l EWMA – In order to capture the dynamic features of volatility it is use an exponential moving average of historical observations, where the latest observations carry the highest weight in volatility estimate – – 9 EWMA depends on the parameter- which is often referred to decay factor. This parameter determines the relative weight of past observations. We have used a decay factor of 0. 94 12 July 2008 Spillover Effect Study

Standard deviations methods - GARCH l A general GARCH (p, q) model is given by Bollerslev, 1986, and the equations specified for this model are: 10 – The conditional mean y (t/t-1) it is take as constant – Conditional variance equation – We have used Garch (1, 1) with Normal and t distribution 12 July 2008 Spillover Effect Study

Value at Risk Methods l Historical Simulation uses real historical data to build an empirical density for the portfolio P&L – – l It is the percentile of the empirical distribution corresponding to the confidence level of these distributions We used two size of past observations of 100 and 250 days Delta-Normal is a parametric method based on the assumption that the return are normally distributed. – Va. R is defined as l 11 Where Z is the alpha percentile of the standard normal density 12 July 2008 Spillover Effect Study

Value at Risk Methods l EVT – used to model fat tails. In order to determine Va. R the next steps have to be considered: – The standardized portfolio returns are given from the following formula – – 12 It is choose a threshold “u” to represent the 95 th, 99 th percentile Let y = x + u. when x = z when z exceeds u; The is estimated by the Hill estimator as defined bellow. When the tail parameter is positive then the return distributions is fat tailed The Va. R from the EVT combined with the variance model is calculated as 12 July 2008 Spillover Effect Study

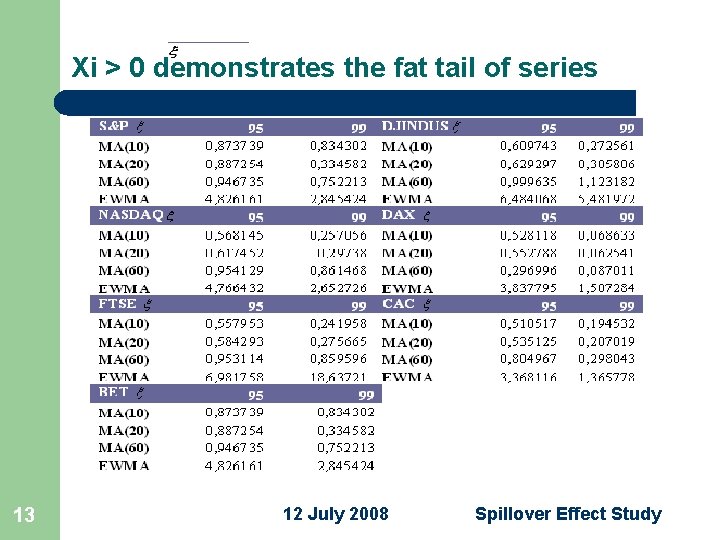
BET CAC FTSE DAX NASDAQ DJINDUS S&P Xi > 0 demonstrates the fat tail of series 13 12 July 2008 Spillover Effect Study

Backtesting l Va. R models must be accompanied by a validation. When the model is perfectly calibrated the number of observations falling outside VAR should be in line with the confidence level l Kupiec (1995) develops approximate 95 percent confidence regions for such a test. . l These regions are defined by the tail points of the log-likelihood ratio: l The LR is asymptotically distributed chi-square with one degree of freedom under the null hypothesis that is the probability. It is reject the null hypothesis if LR> 3. 84 (critical value) 14 12 July 2008 Spillover Effect Study

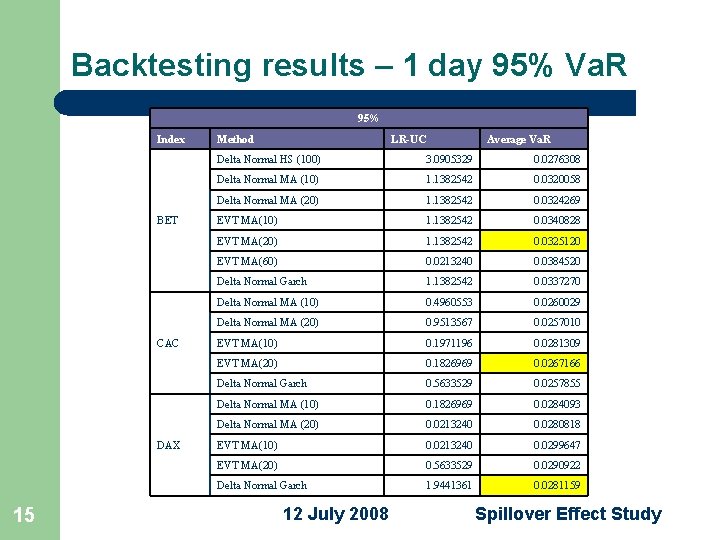
Backtesting results – 1 day 95% Va. R 95% Index BET CAC DAX 15 Method LR-UC Average Va. R Delta Normal HS (100) 3. 0905329 0. 0276308 Delta Normal MA (10) 1. 1382542 0. 0320058 Delta Normal MA (20) 1. 1382542 0. 0324269 EVT MA(10) 1. 1382542 0. 0340828 EVT MA(20) 1. 1382542 0. 0325120 EVT MA(60) 0. 0213240 0. 0384520 Delta Normal Garch 1. 1382542 0. 0337270 Delta Normal MA (10) 0. 4960553 0. 0260029 Delta Normal MA (20) 0. 9513567 0. 0257010 EVT MA(10) 0. 1971196 0. 0281309 EVT MA(20) 0. 1826969 0. 0267166 Delta Normal Garch 0. 5633529 0. 0257855 Delta Normal MA (10) 0. 1826969 0. 0284093 Delta Normal MA (20) 0. 0213240 0. 0280818 EVT MA(10) 0. 0213240 0. 0299647 EVT MA(20) 0. 5633529 0. 0290922 Delta Normal Garch 1. 9441361 0. 0281159 12 July 2008 Spillover Effect Study

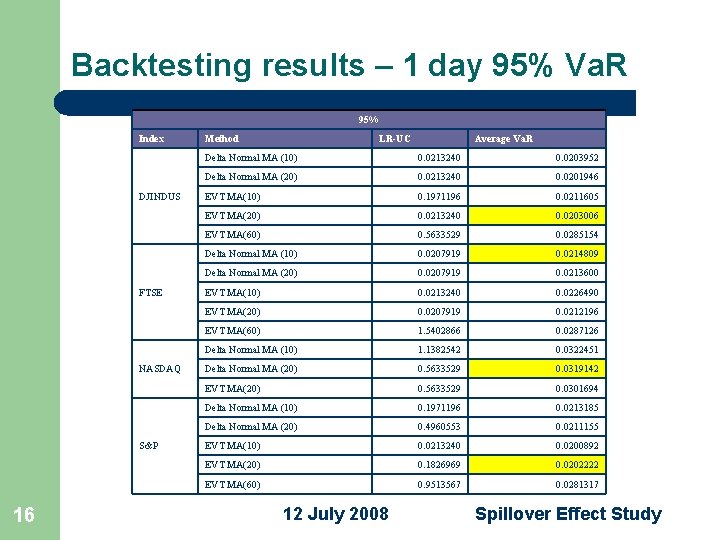
Backtesting results – 1 day 95% Va. R 95% Index DJINDUS FTSE NASDAQ S&P 16 Method LR-UC Average Va. R Delta Normal MA (10) 0. 0213240 0. 0203952 Delta Normal MA (20) 0. 0213240 0. 0201946 EVT MA(10) 0. 1971196 0. 0211605 EVT MA(20) 0. 0213240 0. 0203006 EVT MA(60) 0. 5633529 0. 0285154 Delta Normal MA (10) 0. 0207919 0. 0214809 Delta Normal MA (20) 0. 0207919 0. 0213600 EVT MA(10) 0. 0213240 0. 0226490 EVT MA(20) 0. 0207919 0. 0212196 EVT MA(60) 1. 5402866 0. 0287126 Delta Normal MA (10) 1. 1382542 0. 0322451 Delta Normal MA (20) 0. 5633529 0. 0319142 EVT MA(20) 0. 5633529 0. 0301694 Delta Normal MA (10) 0. 1971196 0. 0213185 Delta Normal MA (20) 0. 4960553 0. 0211155 EVT MA(10) 0. 0213240 0. 0200892 EVT MA(20) 0. 1826969 0. 0202222 EVT MA(60) 0. 9513567 0. 0281317 12 July 2008 Spillover Effect Study

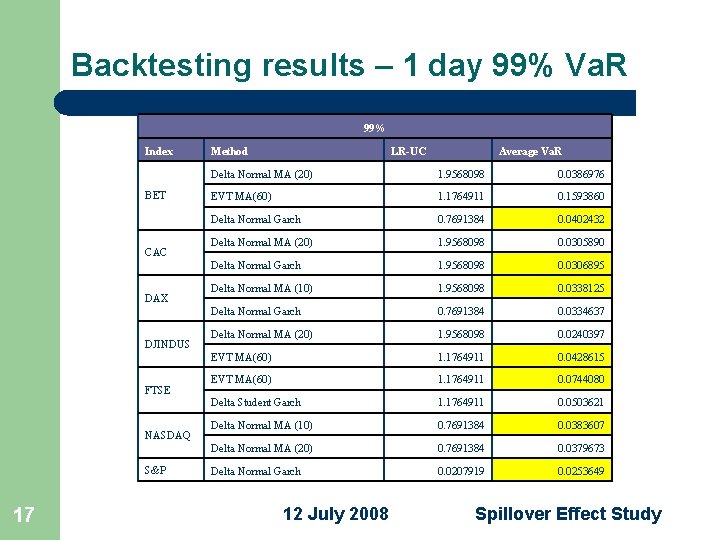
Backtesting results – 1 day 99% Va. R 99% Index BET CAC DAX DJINDUS FTSE NASDAQ S&P 17 Method LR-UC Average Va. R Delta Normal MA (20) 1. 9568098 0. 0386976 EVT MA(60) 1. 1764911 0. 1593860 Delta Normal Garch 0. 7691384 0. 0402432 Delta Normal MA (20) 1. 9568098 0. 0305890 Delta Normal Garch 1. 9568098 0. 0306895 Delta Normal MA (10) 1. 9568098 0. 0338125 Delta Normal Garch 0. 7691384 0. 0334637 Delta Normal MA (20) 1. 9568098 0. 0240397 EVT MA(60) 1. 1764911 0. 0428615 EVT MA(60) 1. 1764911 0. 0744080 Delta Student Garch 1. 1764911 0. 0503621 Delta Normal MA (10) 0. 7691384 0. 0383607 Delta Normal MA (20) 0. 7691384 0. 0379673 Delta Normal Garch 0. 0207919 0. 0253649 12 July 2008 Spillover Effect Study

Backtesting conclusion 18 l Extreme Value Theory estimates better the 95% Va. R l 99% Va. R estimation is split between Delta Normal Garch, EVT and Delta Normal Moving Average 12 July 2008 Spillover Effect Study

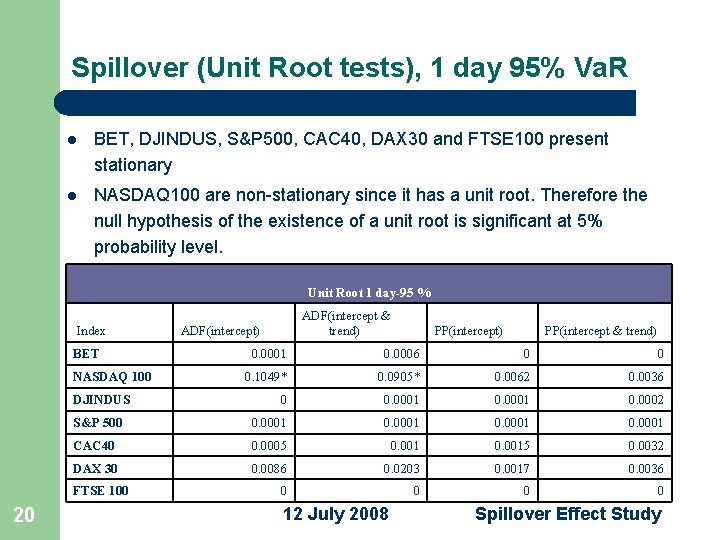
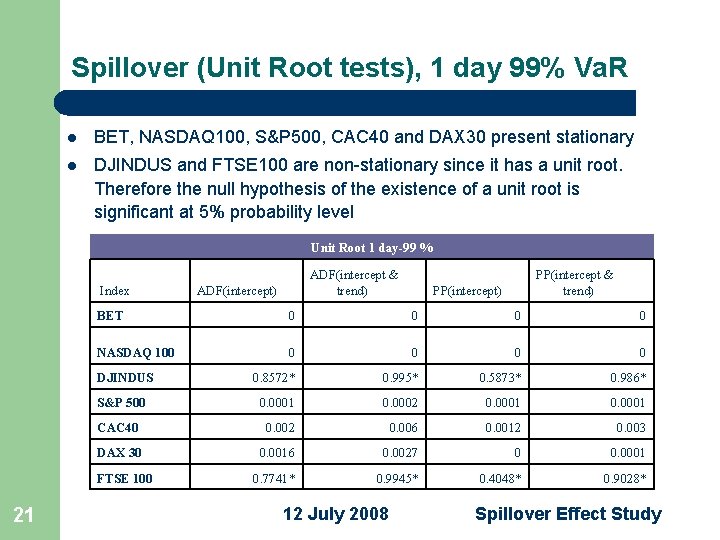
Spillover (Unit Root tests) 19 l In order to proceed further we need to study the stationarity of the series l Two methods used: – Augmented Dickey-Fuller (1981) test - takes care of the deterministic part – Philips-Perron - focuses on the stochastic part of the drift 12 July 2008 Spillover Effect Study

Spillover (Unit Root tests), 1 day 95% Va. R l BET, DJINDUS, S&P 500, CAC 40, DAX 30 and FTSE 100 present stationary l NASDAQ 100 are non-stationary since it has a unit root. Therefore the null hypothesis of the existence of a unit root is significant at 5% probability level. Unit Root 1 day-95 % Index BET ADF(intercept) PP(intercept & trend) 0. 0001 0. 0006 0 0 0. 1049* 0. 0905* 0. 0062 0. 0036 0 0. 0001 0. 0002 S&P 500 0. 0001 CAC 40 0. 0005 0. 0015 0. 0032 DAX 30 0. 0086 0. 0203 0. 0017 0. 0036 0 0 NASDAQ 100 DJINDUS FTSE 100 20 ADF(intercept & trend) 12 July 2008 Spillover Effect Study

Spillover (Unit Root tests), 1 day 99% Va. R l BET, NASDAQ 100, S&P 500, CAC 40 and DAX 30 present stationary l DJINDUS and FTSE 100 are non-stationary since it has a unit root. Therefore the null hypothesis of the existence of a unit root is significant at 5% probability level Unit Root 1 day-99 % Index ADF(intercept) PP(intercept & trend) PP(intercept) BET 0 0 NASDAQ 100 0 0 DJINDUS 0. 8572* 0. 995* 0. 5873* 0. 986* S&P 500 0. 0001 0. 0002 0. 0001 CAC 40 0. 002 0. 006 0. 0012 0. 003 DAX 30 0. 0016 0. 0027 0 0. 0001 0. 7741* 0. 9945* 0. 4048* 0. 9028* FTSE 100 21 ADF(intercept & trend) 12 July 2008 Spillover Effect Study

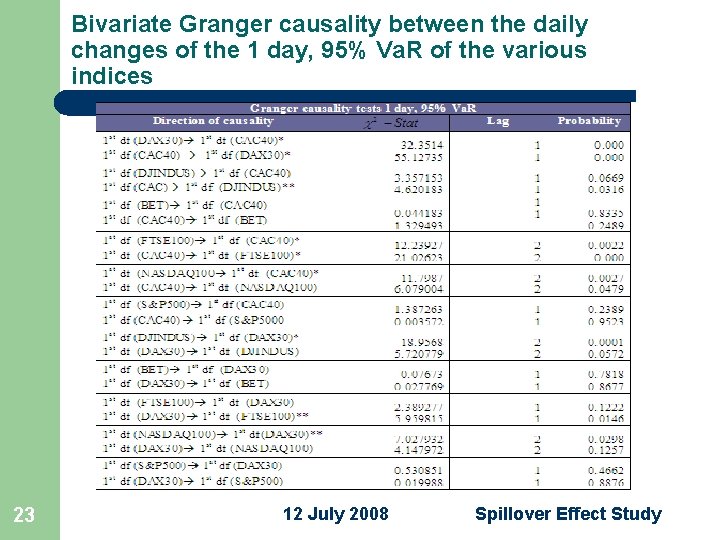
Spillover – Granger Causality 22 l In order to test for Granger causality across two variables X and Y we run bivariate regressions with a lag length set as k. These are called unrestricted regressions: l Granger Causality is examined by testing the null hypothesis whether all are equal to zero 12 July 2008 Spillover Effect Study

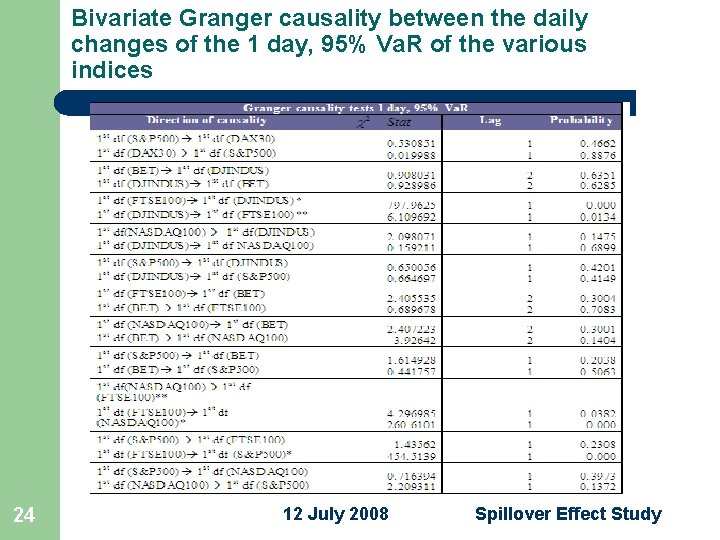
Bivariate Granger causality between the daily changes of the 1 day, 95% Va. R of the various indices 23 12 July 2008 Spillover Effect Study

Bivariate Granger causality between the daily changes of the 1 day, 95% Va. R of the various indices 24 12 July 2008 Spillover Effect Study

Bivariate Granger causality between the daily changes of the 1 day, 95% Va. R of the various indices l at 1% probability level, there is a spillover effect from: – FTSE 100 to l l – CAC 40 to l – DAX 30 NASDAQ 100 to l 25 CAC 40 to l – FTSE 100 DAX 30 to l – CAC 40 DJINDUS NASDAQ 100 S&P 500 CAC 40 12 July 2008 Spillover Effect Study

Bivariate Granger causality between the daily changes of the 1 day, 95% Va. R of the various indices l at 5% probability level, there is a spillover effect from: – DAX 30 to l – NASADQ 100 to l l – DAX 30, FTSE 100 DJINDUS to l 26 FTSE 100 12 July 2008 Spillover Effect Study

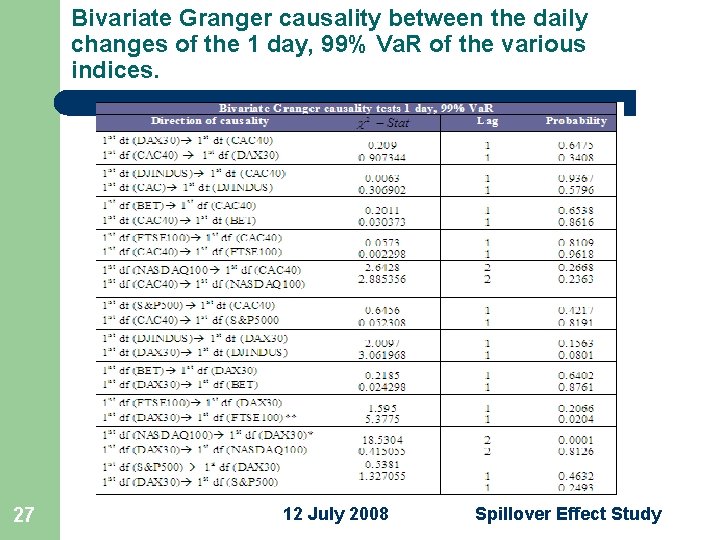
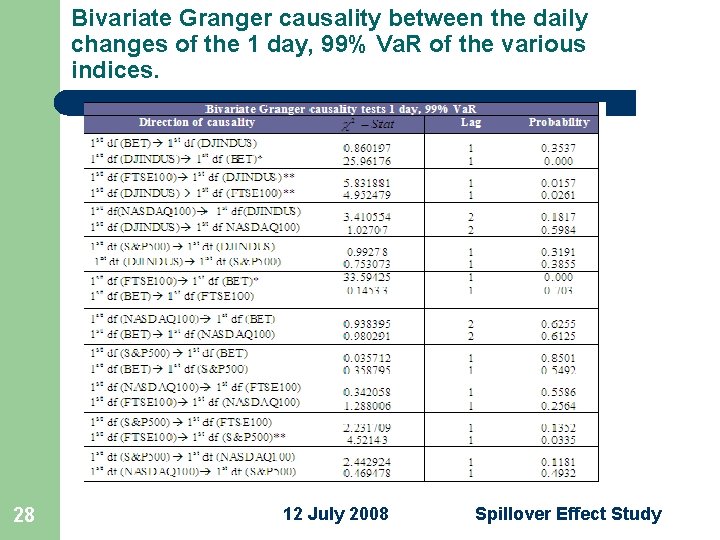
Bivariate Granger causality between the daily changes of the 1 day, 99% Va. R of the various indices. 27 12 July 2008 Spillover Effect Study

Bivariate Granger causality between the daily changes of the 1 day, 99% Va. R of the various indices. 28 12 July 2008 Spillover Effect Study

Bivariate Granger causality between the daily changes of the 1 day, 99% Va. R of the various indices. l at 1% probability level there is a spillover effect from: – NASDAQ 100 to l – DJINDUS to l – BET FTSE 100 to l 29 DAX 30, BET 12 July 2008 Spillover Effect Study

Bivariate Granger causality between the daily changes of the 1 day, 99% Va. R of the various indices. l at 5% probability level there is a spillover effect from: – DAX 30 to l – FTSE 100 to l l – DJINDUS S&P 500 DJINDUS to l 30 FTSE 100 12 July 2008 Spillover Effect Study

Topics l l 31 Introduction Methodologies used and results Conclusion References-Annex 12 July 2008 Spillover Effect Study

Conclusion (1) l l l 32 There is are spillover effects from US and European market to Romanian market, especially from DJINDUS and FTSE 100. Comparing the two different levels of risk (95 % and 99%) we observe that for the 95% Va. R there are more spillover effects across the markets But, as per 99% Va. R calculations, the US and European markets influence the Romanian capital market 12 July 2008 Spillover Effect Study

Conclusion (2) l l l 33 US indexes have the greatest effect across the indexes, in particular DJ INDUSTRIALS and NASDAQ 100 Another interesting result is that FTSE 100 plays a significant role since it leads many other markets. Also we have found a causal relationship between DAC 30 and CAC 40 to European market. 12 July 2008 Spillover Effect Study

Conclusions beyond formulas l l 34 Globalisation has an important role in the correlations between markets. Big players have access to all the markets and usually they have a unitary strategy that will influence accordingly all the markets on which they are active Investors expectations triggers also the correlations between markets. If they see an upward or downward move on other important markets they will expect the same move on their market. Hence they will buy or sell accordingly 12 July 2008 Spillover Effect Study

Topics l l 35 Introduction Methodologies used and results Conclusion References-Annex 12 July 2008 Spillover Effect Study

References-Annex l l l l l 36 Fama, E. , 1965, The Behavior of Stock Market Prices, Journal of Business, vol 38. nr 1, page. 34 -105 Engle R. , 2004, Risk and Volatility, Econometric Models and Financial Practice, vol 94, nr. 3, page. 405 -420 Hamao, Y. , Masulis, R. W. , Ng, V. , 1990, Correlations in Price Changes and Volatility Across International Stock Markets, Review of Financial Studies 3. , nr 2, page 281 -307 Martens, M. , Poon, S. H. , 2000, Returns Synchronization and Daily Correlation Dynamics, Journal of Banking and Finance Wen- Ling-Lin, Robert F. Engle, Takatoski, 1994, Do bulls and bears move across borders? International transmission of Stock returns and Volatility, The Review of Financial Studies, vol. 7, nr. 3, page. 507 -538 Bollerslev T. , 1987, A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return, The Review of Economics and Statistics, vol 69, nr. 3, page. 542 -547 Poon s. H. , M. Rockinger, J. Tawn, 2004, Extreme Value dependence in Financial Market- Diagnostics, Models and Financial Implications, Review of Financial Studies, vol. 17. nr. 2. , page. 581 -610 Stanley J. K. , 1984, Models of Stock Returns – A Comparison, the Journal of Finance, vol. 39. , nr 1, page. 147 -165 Lee S. J, 2006, Volatility spillover among Six Asian Countries and US, Financial Supervisory Service South Korea 12 July 2008 Spillover Effect Study

References-Annex l l l l l 37 Nylud S. , 2001, Value at Risk Analysis for Heavy- Tailed Financial Returns, Helsinki University of Technology, Department of Engineering Physics and Mathematics Granger, C. J. , 1969, "Investigating Causal Relationships by Econometrics Models and Cross Spectral Methods. " Econometrica, Vol. 37. Hiemstra C. , D. J. Jonathan, 1994, Testing for linear and non-linear Granger causality in Stock Prices – The Journal of Finance, vol. 49. Nr. 5. Page. 16391664 Engle R. , 2001, The use of ARCH/GARCH Models in Applied econometrics, The Journal of Economic Perspectives, vol. 15, nr 4, page 157 -168 Thomas S. Y. Ho, S. B. Lee (2004) , The Oxford Guide to financial Modeling. Applications for Capital Markets, Corporate Finance, Risk Management and Financial Institution Hull, J. , Options, Futures and Other Derivatives, 6 th edition. Morgan J. P. , December 1996, Risk Metrics - Technical Document, 4 th edition Alexander C. (2001), A Guide to Financial Data Analysis Jorion P. (2002), Managing Financial Risk- Value at Risk 12 July 2008 Spillover Effect Study

Thank you!