Spherical Extent Functions Spherical Extent Function Spherical Extent

Spherical Extent Function A model is represented by its star-shaped envelope: – The minimal

Spherical Extent Function Properties: – Invertible for star-shaped models – 2 D array of

Spherical Extent Function Properties: – Can be defined for most models – Invertible for

PCA Alignment Treat a surface as a collection of points and define the variance

PCA Alignment Define the covariance matrix M: Find the eigen-values and align so that

PCA Alignment Limitation: – Eigen-values are only defined up to sign! PCA alignment is

Spherical Functions Parameterize points on the sphere in terms of angles [0, ] and

Spherical Functions Every spherical function can be expressed as the sum of spherical harmonics

Spherical Harmonics Every spherical function can be expressed as the sum of spherical harmonics

Spherical Harmonics If f is a spherical function: Then storing just the absolute values:

Slides: 16

Download presentation

Spherical Extent Functions

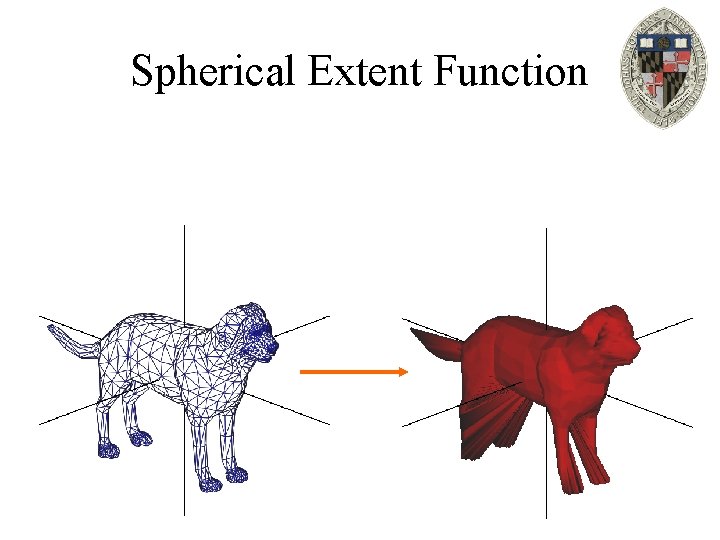
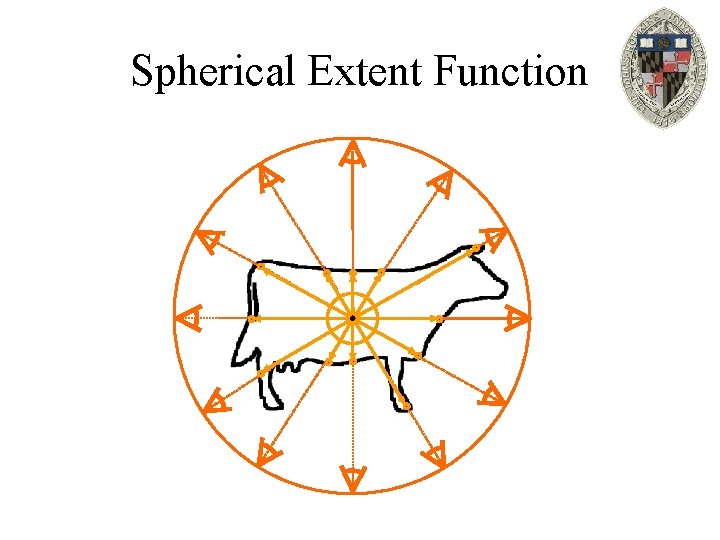
Spherical Extent Function

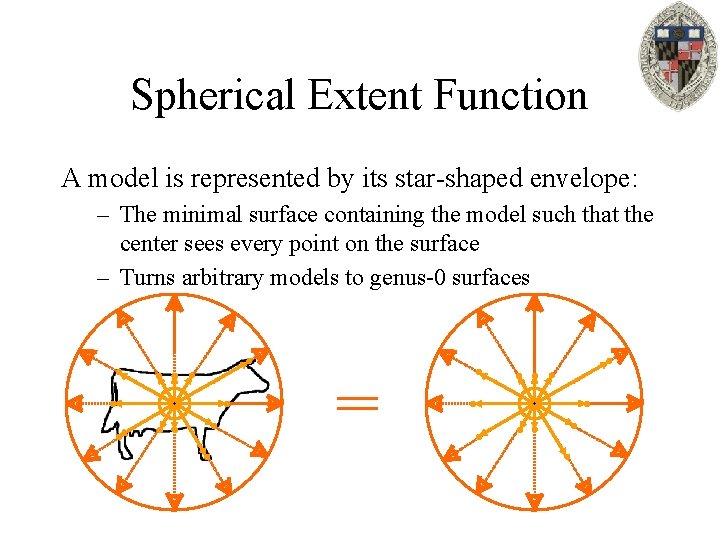
Spherical Extent Function A model is represented by its star-shaped envelope: – The minimal surface containing the model such that the center sees every point on the surface – Turns arbitrary models to genus-0 surfaces

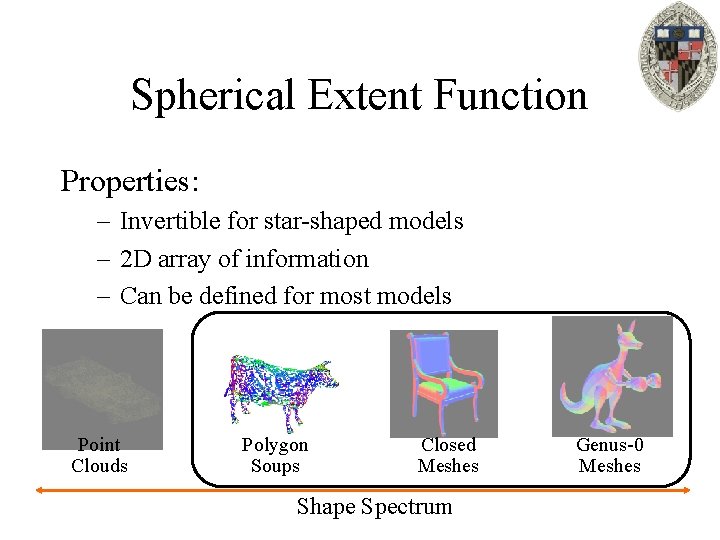
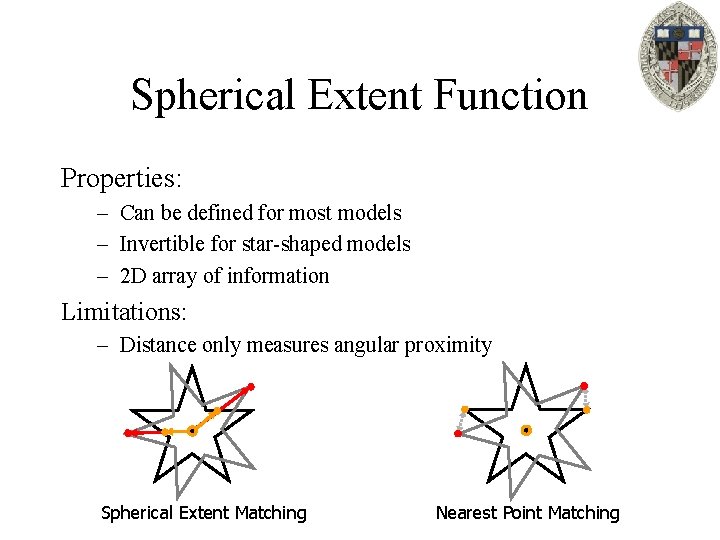
Spherical Extent Function Properties: – Invertible for star-shaped models – 2 D array of information – Can be defined for most models Point Clouds Polygon Soups Closed Meshes Shape Spectrum Genus-0 Meshes

Spherical Extent Function Properties: – Can be defined for most models – Invertible for star-shaped models – 2 D array of information Limitations: – Distance only measures angular proximity Spherical Extent Matching Nearest Point Matching

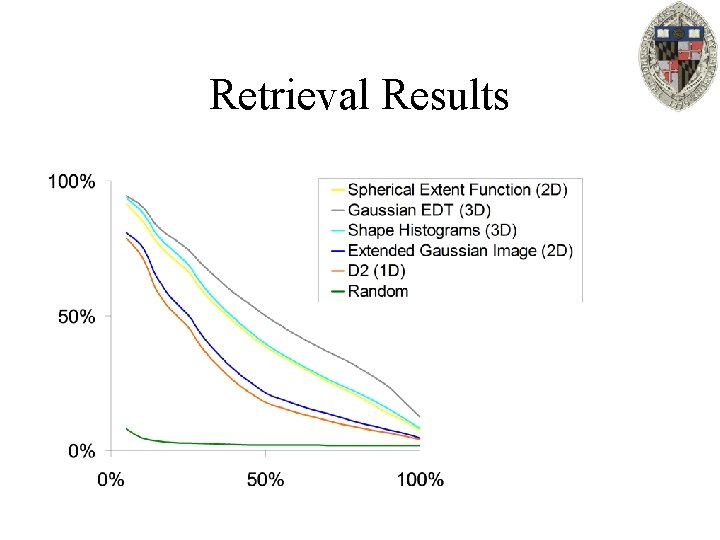
Retrieval Results

PCA Alignment Treat a surface as a collection of points and define the variance function:

PCA Alignment Define the covariance matrix M: Find the eigen-values and align so that the eigen-values map to the x-, y-, and z-axes

PCA Alignment Limitation: – Eigen-values are only defined up to sign! PCA alignment is only well-defined up to axial flips about the x-, y-, and z-axes.

Spherical Functions Parameterize points on the sphere in terms of angles [0, ] and [0, 2 ): z ( , )

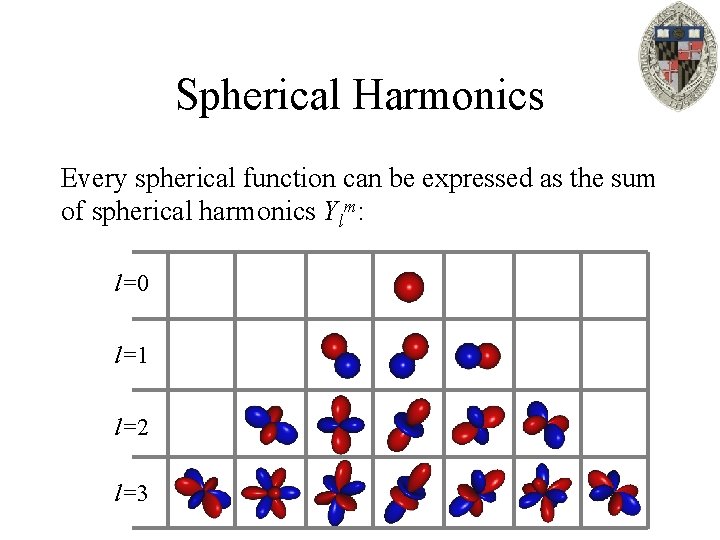
Spherical Functions Every spherical function can be expressed as the sum of spherical harmonics Ylm: Where l is the frequency and m indexes harmonics within a frequency.

Spherical Harmonics Every spherical function can be expressed as the sum of spherical harmonics Ylm: l=0 l=1 l=2 l=3

Spherical Harmonics Every spherical function can be expressed as the sum of spherical harmonics Ylm: Rotation by 0 gives:

Spherical Harmonics If f is a spherical function: Then storing just the absolute values: gives a representation of f that is: 1. Invariant to rotation by 0. 2. Invariant to axial flips about the x-, y-, and z-axes.