SPEZZATA POLIGONALE Pi segmenti consecutivi formano una linea

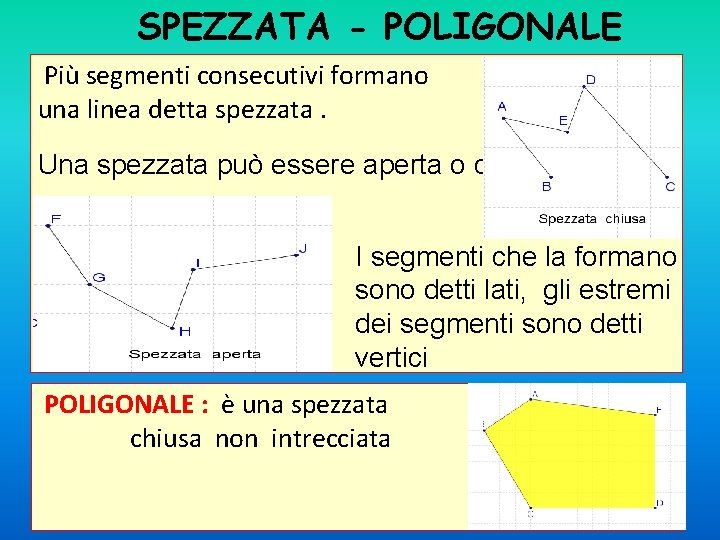
SPEZZATA - POLIGONALE Più segmenti consecutivi formano una linea detta spezzata. Una spezzata può essere aperta o chiusa. I segmenti che la formano sono detti lati, gli estremi dei segmenti sono detti vertici POLIGONALE : è una spezzata chiusa non intrecciata

POLIGONI Si dice poligono una figura formata da una poligonale e dai punti del piano interni ad essa Un poligono si dice convesso se il segmento che unisce due suoi punti qualsiasi è tutto interno al poligono Un poligono si dice concavo se il segmento che unisce due suoi punti qualsiasi non è tutto interno al poligono Corda è un segmento che unisce due punti qualsiasi del contorno del poligono che non appartengono allo stesso lato. Diagonale è ogni segmento che unisce due vertici non consecutivi.

QUADRILATERI • I quadrilateri sono poligoni con : • quattro lati • Quattro vertici • Quattro angoli • Due diagonali • Classificazione dei quadrilateri • Trapezi • Parallelogrammi • Rettangoli • Quadrati • Rombi

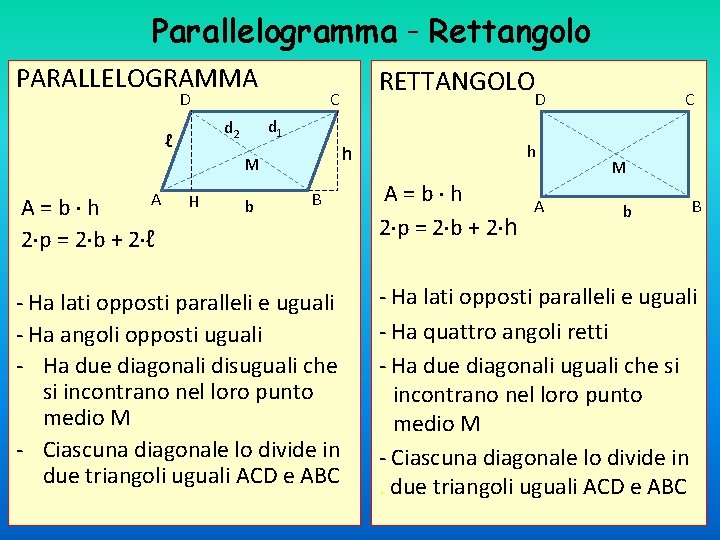
Parallelogramma - Rettangolo PARALLELOGRAMMA D C H b h h M A A=b h 2 p = 2 b + 2 ℓ D d 1 d 2 ℓ RETTANGOLO B - Ha lati opposti paralleli e uguali - Ha angoli opposti uguali - Ha due diagonali disuguali che si incontrano nel loro punto medio M - Ciascuna diagonale lo divide in due triangoli uguali ACD e ABC A=b h 2 p = 2 b + 2 h A C M b B - Ha lati opposti paralleli e uguali - Ha quattro angoli retti - Ha due diagonali uguali che si incontrano nel loro punto medio M - Ciascuna diagonale lo divide in. due triangoli uguali ACD e ABC

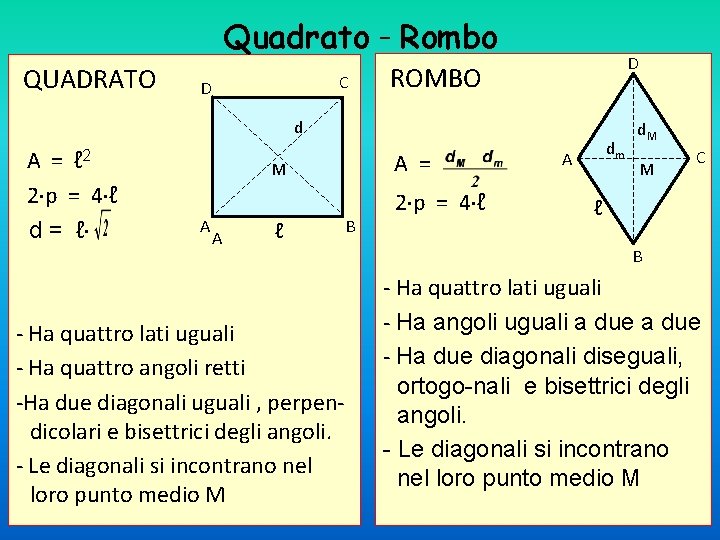
Quadrato - Rombo QUADRATO C D D ROMBO d A = ℓ 2 2 p = 4 ℓ d = ℓ A = M A A ℓ - Ha quattro lati uguali - Ha quattro angoli retti -Ha due diagonali uguali , perpendicolari e bisettrici degli angoli. - Le diagonali si incontrano nel loro punto medio M B 2 p = 4 ℓ dm A d. M M C ℓ B - Ha quattro lati uguali - Ha angoli uguali a due - Ha due diagonali diseguali, ortogo-nali e bisettrici degli angoli. - Le diagonali si incontrano nel loro punto medio M

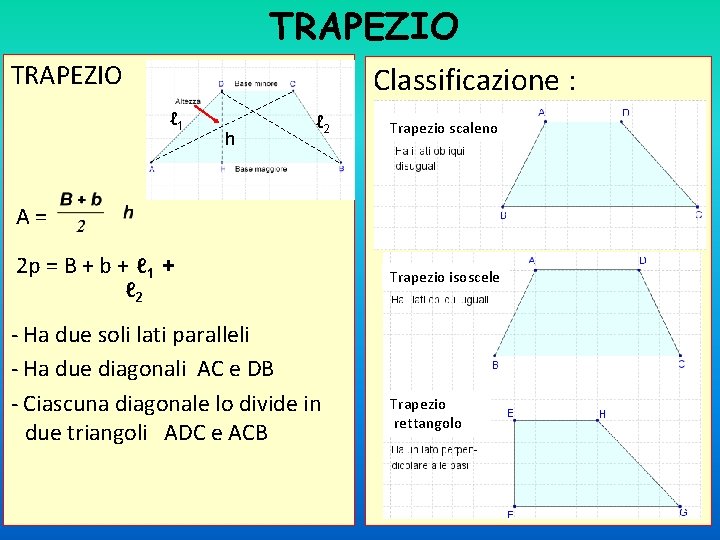
TRAPEZIO Classificazione : ℓ 1 h ℓ 2 Trapezio scaleno A= 2 p = B + b + ℓ 1 + ℓ 2 - Ha due soli lati paralleli - Ha due diagonali AC e DB - Ciascuna diagonale lo divide in due triangoli ADC e ACB Trapezio isoscele Trapezio rettangolo

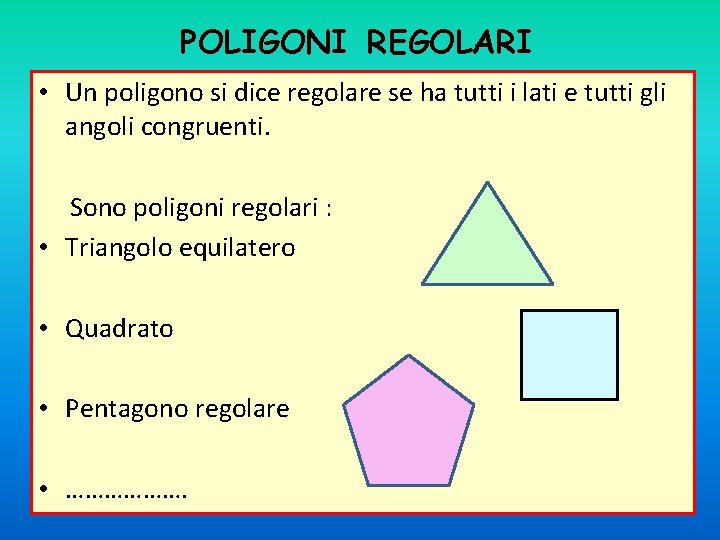
POLIGONI REGOLARI • Un poligono si dice regolare se ha tutti i lati e tutti gli angoli congruenti. Sono poligoni regolari : • Triangolo equilatero • Quadrato • Pentagono regolare • ……………….

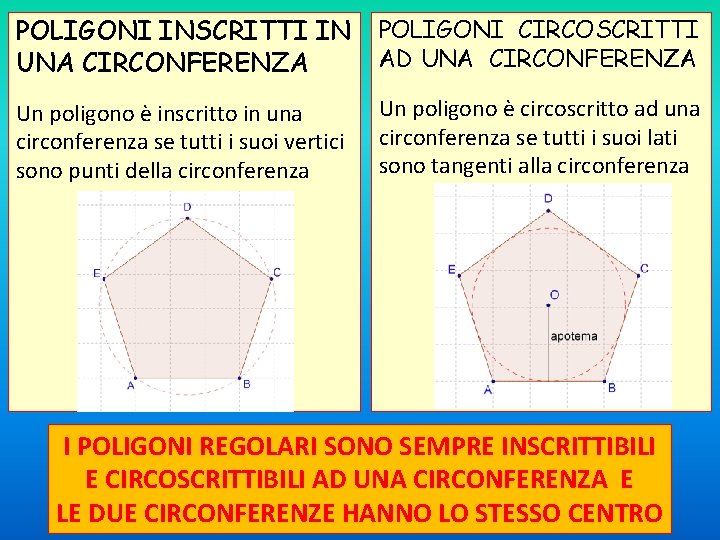
POLIGONI INSCRITTI IN UNA CIRCONFERENZA POLIGONI CIRCOSCRITTI AD UNA CIRCONFERENZA Un poligono è inscritto in una circonferenza se tutti i suoi vertici sono punti della circonferenza Un poligono è circoscritto ad una circonferenza se tutti i suoi lati sono tangenti alla circonferenza I POLIGONI REGOLARI SONO SEMPRE INSCRITTIBILI E CIRCOSCRITTIBILI AD UNA CIRCONFERENZA E LE DUE CIRCONFERENZE HANNO LO STESSO CENTRO

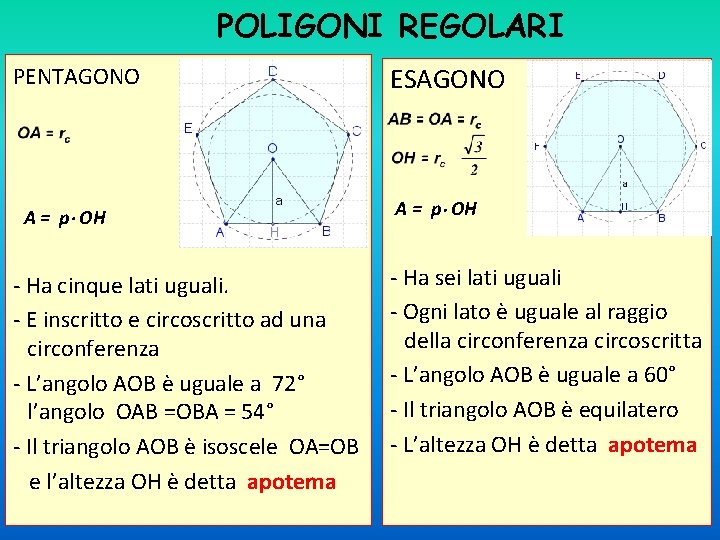
POLIGONI REGOLARI PENTAGONO A = p OH - Ha cinque lati uguali. - E inscritto e circoscritto ad una circonferenza - L’angolo AOB è uguale a 72° l’angolo OAB =OBA = 54° - Il triangolo AOB è isoscele OA=OB e l’altezza OH è detta apotema ESAGONO A = p OH - Ha sei lati uguali - Ogni lato è uguale al raggio della circonferenza circoscritta - L’angolo AOB è uguale a 60° - Il triangolo AOB è equilatero - L’altezza OH è detta apotema