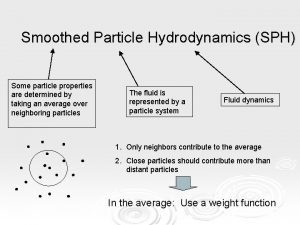
SPERIC Training Day Introduction to Smoothed Particle Hydrodynamics

SPERIC Training Day Introduction to Smoothed Particle Hydrodynamics Stefano Sibilla Department of Civil Engineering and Architecture University of Pavia SPHERIC 2015 - Parma June 15, 2015

Lesson schedule • • • Lagrangian methods in fluid mechanics • • • Navier-Stokes equations in Lagrangian form Kernel approximation of a function and its derivative Discretization: smoothed particle approximation Consistency issues in SPH: boundaries and particle disorder Renormalization of the kernel function and of its gradient Examples of kernel functions SPH formulation of the Navier-Stokes equations Weakly Compressible vs. Incompressible SPH Neighbour search algorithms Wall boundary treatment: ghost particles, barrier particles, integral conditions Inflow and outflow boundaries SPHERIC 2015 - Parma June 15, 2015

Continuum mechanics • Phenomena described by PDEs in space-time • Solution feasible only via numerical analysis • Numerical analysis requires: • Discretization of the geometry (e. g. space or mass) • Discretization of the governing PDEs • Solution algorithm suitable to PDEs character (e. g. for 2 nd order PDEs: hyperbolic, parabolic or elliptic) SPHERIC 2015 - Parma June 15, 2015

Lagrangian vs. Eulerian • Conservation of a mass-dependent property G can be written either: • by considering its time evolution for a given mass (or point mass): Lagrangian description • by considering its time evolution within a given (infinitesimal) volume fixed in space: Eulerian description • Numerical methods can be equivalently based on both descriptions SPHERIC 2015 - Parma June 15, 2015

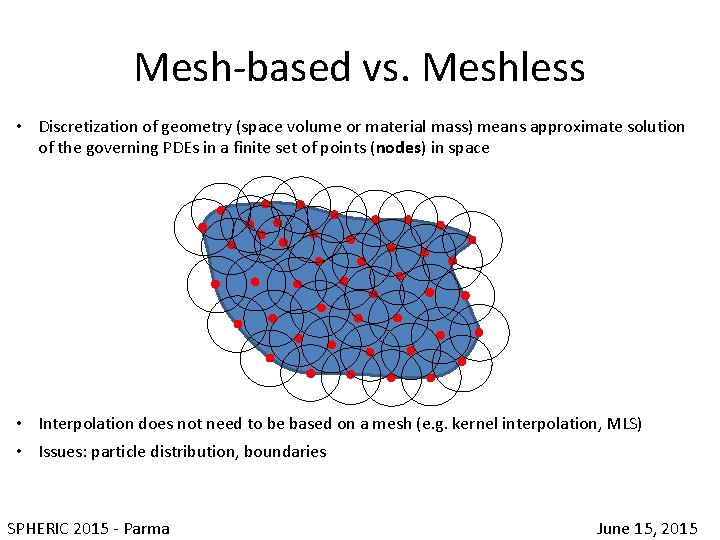
Mesh-based vs. Meshless • Discretization of geometry (space volume or material mass) means approximate solution of the governing PDEs in a finite set of points (nodes) in space • These points can (not: need to) be connected by fixed topological links (mesh) • Approximate (i. e. numerical) solution needs necessarily: • proper interpolation of conserved properties far from the nodes • proper discretization of the differential operators in the PDEs SPHERIC 2015 - Parma June 15, 2015

Mesh-based example: FEM • Governing conservation PDE: • Interpolation • Discretization (W = Nj) SPHERIC 2015 - Parma June 15, 2015

Mesh-based vs. Meshless • Discretization of geometry (space volume or material mass) means approximate solution of the governing PDEs in a finite set of points (nodes) in space • Interpolation does not need to be based on a mesh (e. g. kernel interpolation, MLS) • Issues: particle distribution, boundaries SPHERIC 2015 - Parma June 15, 2015

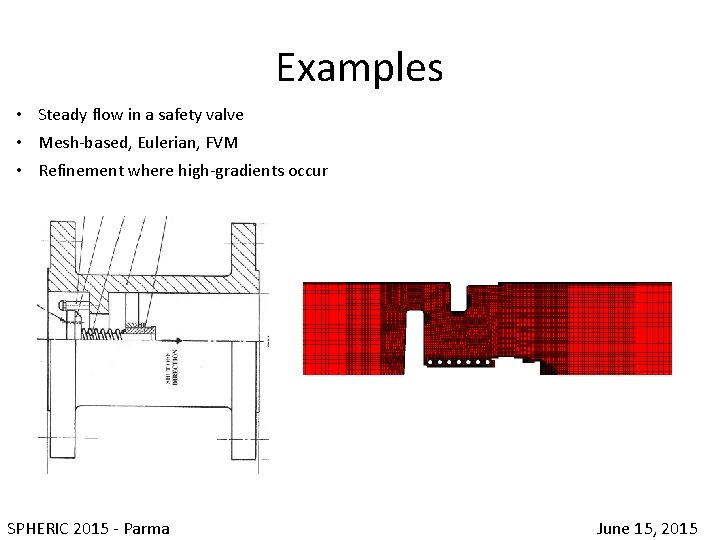
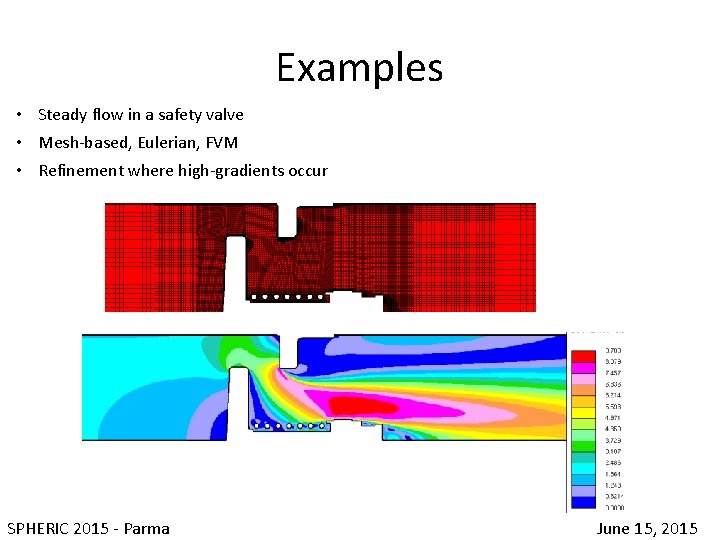
Examples • Steady flow in a safety valve • Mesh-based, Eulerian, FVM • Refinement where high-gradients occur SPHERIC 2015 - Parma June 15, 2015

Examples • Steady flow in a safety valve • Mesh-based, Eulerian, FVM • Refinement where high-gradients occur SPHERIC 2015 - Parma June 15, 2015

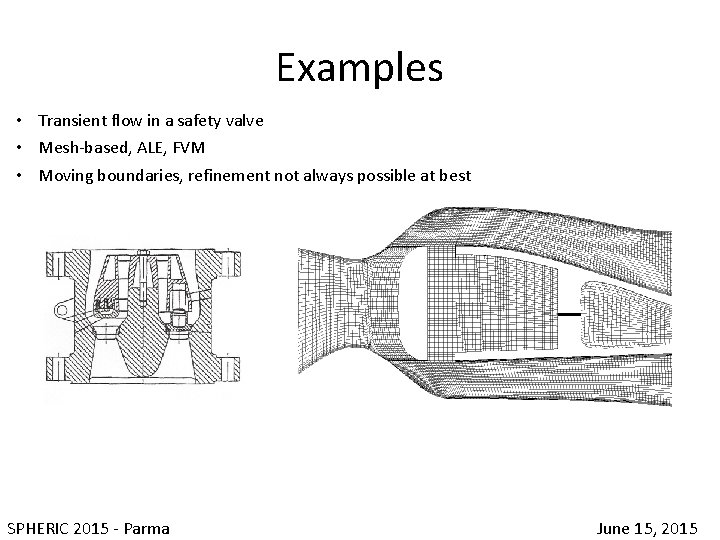
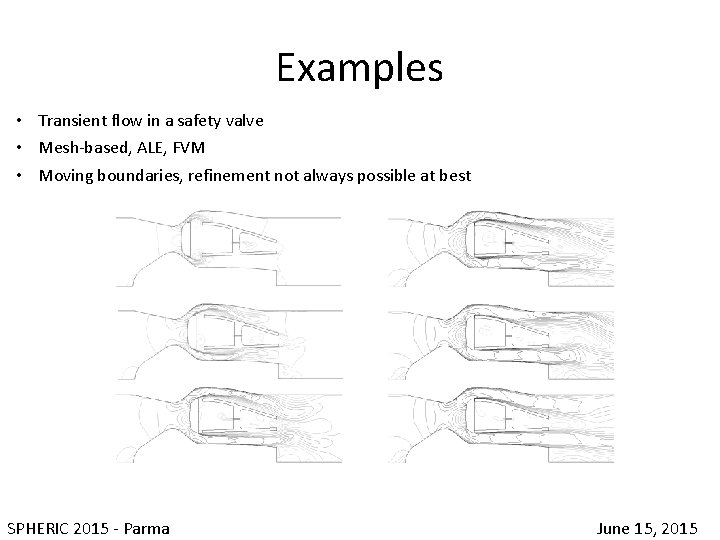
Examples • Transient flow in a safety valve • Mesh-based, ALE, FVM • Moving boundaries, refinement not always possible at best SPHERIC 2015 - Parma June 15, 2015

Examples • Transient flow in a safety valve • Mesh-based, ALE, FVM • Moving boundaries, refinement not always possible at best SPHERIC 2015 - Parma June 15, 2015

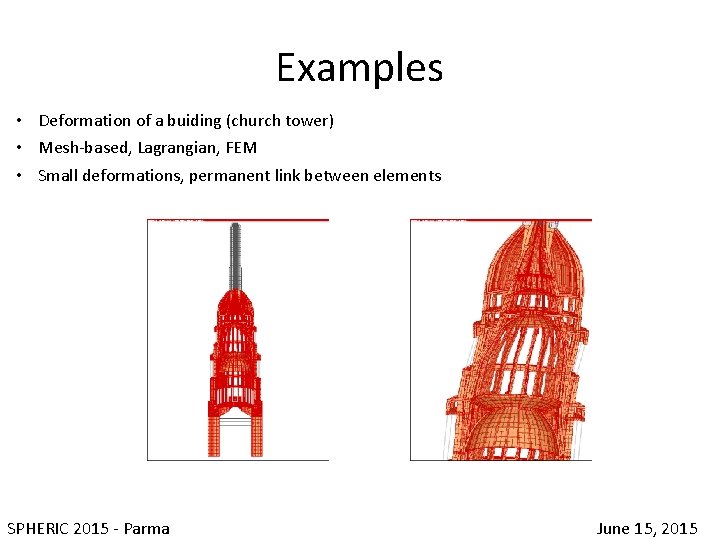
Examples • Deformation of a buiding (church tower) • Mesh-based, Lagrangian, FEM • Small deformations, permanent link between elements SPHERIC 2015 - Parma June 15, 2015

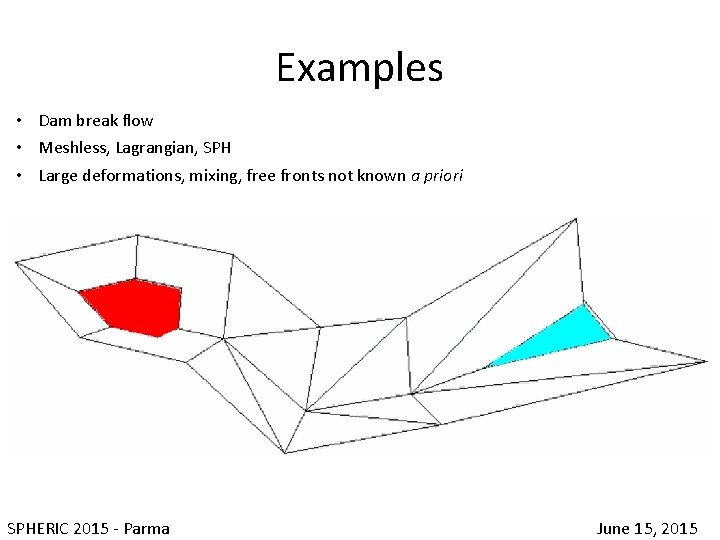
Examples • Dam break flow • Meshless, Lagrangian, SPH • Large deformations, mixing, free fronts not known a priori SPHERIC 2015 - Parma June 15, 2015

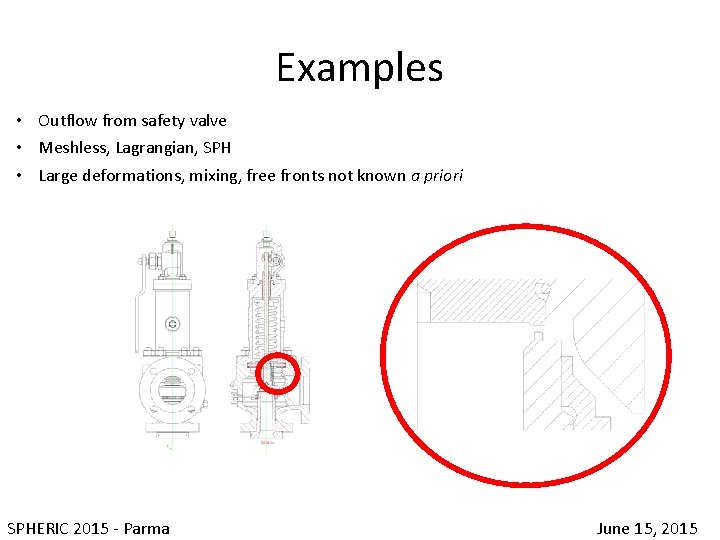
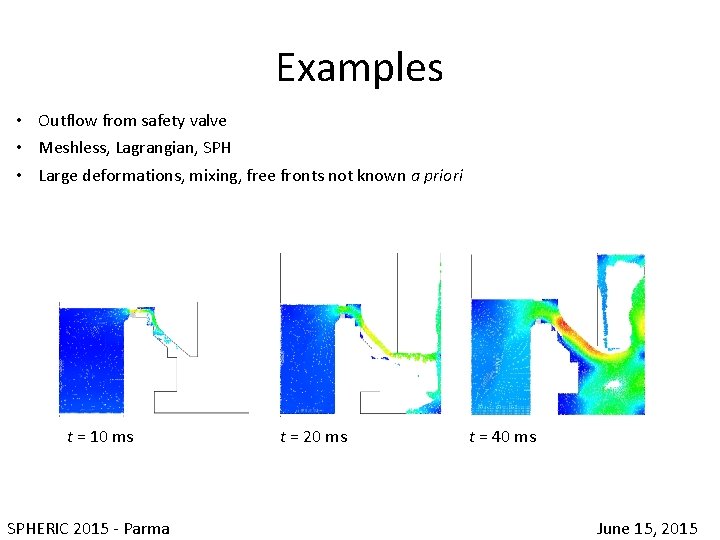
Examples • Outflow from safety valve • Meshless, Lagrangian, SPH • Large deformations, mixing, free fronts not known a priori SPHERIC 2015 - Parma June 15, 2015

Examples • Outflow from safety valve • Meshless, Lagrangian, SPH • Large deformations, mixing, free fronts not known a priori t = 10 ms t = 20 ms t = 40 ms SPHERIC 2015 - Parma June 15, 2015

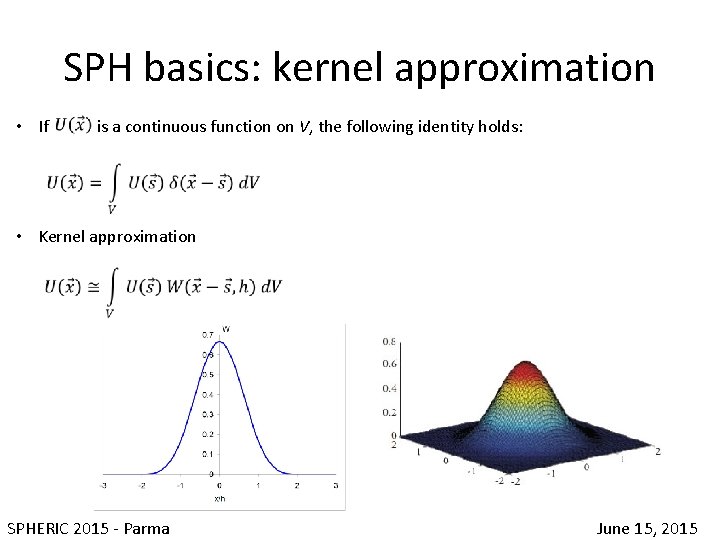
SPH basics: kernel approximation • If is a continuous function on V, the following identity holds: • Kernel approximation SPHERIC 2015 - Parma June 15, 2015

Kernel properties To approximate the Dirac d function, must have the following properties: • usually isotropic (even function) • defined on a compact support W : • tending to the Dirac d function: • normalized: h is defined as the smoothing length SPHERIC 2015 - Parma June 15, 2015

Kernel approximation of derivatives • If is continuous and differentiable on W: • the differential operator can be moved on the kernel (as in FEM with shape functions): SPHERIC 2015 - Parma June 15, 2015

Kernel approximation of derivatives • gradient of a scalar function: • 2 nd order derivatives • Laplacian of a function: …but it will be shown that consistency problems can arise. SPHERIC 2015 - Parma June 15, 2015

From continuum to particles • we study the dynamics of a continuum medium • we approximate the continuum media with elements (particles) of initial volume Vi • we associate a mass (and a density) to each particle i mi = r i V i i SPHERIC 2015 - Parma June 15, 2015

Particle approximation of a function the kernel approximation of the real function U(xi) : W can be written in discrete form: j where the summation is extended to all the particles j for which: ξh i SPHERIC 2015 - Parma June 15, 2015

Particle approximation of derivatives • By discretization of the kernel interpolation formulas we get: • SPH approximation of : ξh • SPH approximation of : i j • and so on… SPHERIC 2015 - Parma June 15, 2015

SPH consistency • Lax theorem of numerical analysis: convergence guaranteed by stability and consistency • kth order consistency: exact reproduction of a kth order polynomial function f(x) 0 th order: f(x) = a 1 st order: f(x) = a x + b 2 nd order: f(x) = a x 2 + b x + c • etc… kth order consistency guarantees (k+1)th order accuracy SPHERIC 2015 - Parma June 15, 2015

0 th order SPH consistency (1 D) f(x) = a • Consistency of the kernel approximation requires: • which implies: • 0 th order kernel consistency is guaranteed by the kernel normalization condition. But… • Particle approximation may not satisfy exactly the 0 th order consistency condition (near boundaries or for non-uniform particle distribution) SPHERIC 2015 - Parma June 15, 2015

1 st order SPH consistency (1 D) f(x) = a x + b • Consistency of the kernel approximation requires: • which, given that • multiplying the normalization condition by xi and subtracting: • consistency guaranteed if the kernel is an even function… • …but particle consistency is not guaranteed a priori , leads to: SPHERIC 2015 - Parma June 15, 2015

1 D kernel functions • Cubic B-spline kernel (Monaghan & Lattanzio, 1985): x = 2

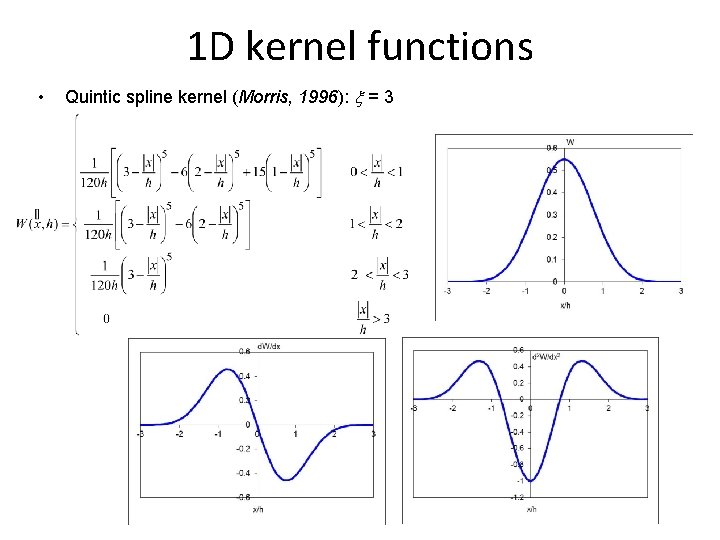
1 D kernel functions • Quintic spline kernel (Morris, 1996): x = 3

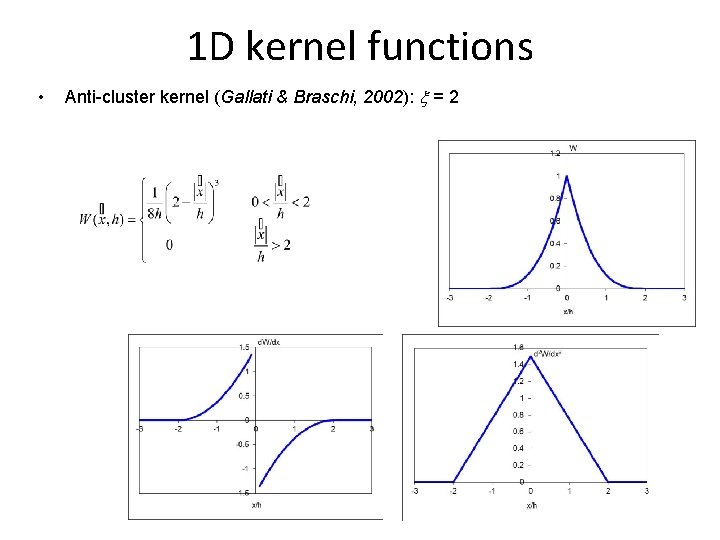
1 D kernel functions • Anti-cluster kernel (Gallati & Braschi, 2002): x = 2

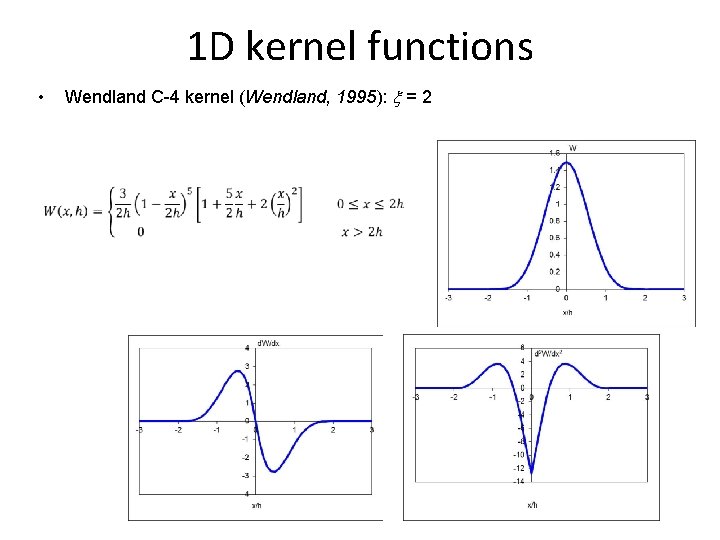
1 D kernel functions • Wendland C-4 kernel (Wendland, 1995): x = 2

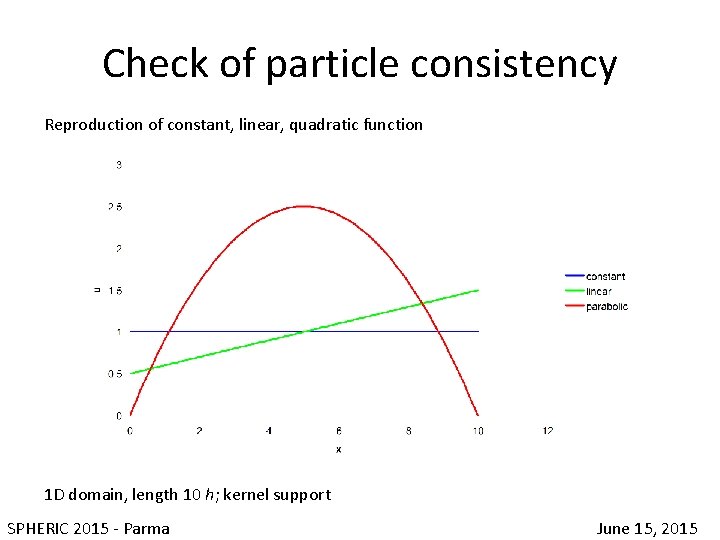
Check of particle consistency Reproduction of constant, linear, quadratic function 1 D domain, length 10 h; kernel support SPHERIC 2015 - Parma June 15, 2015

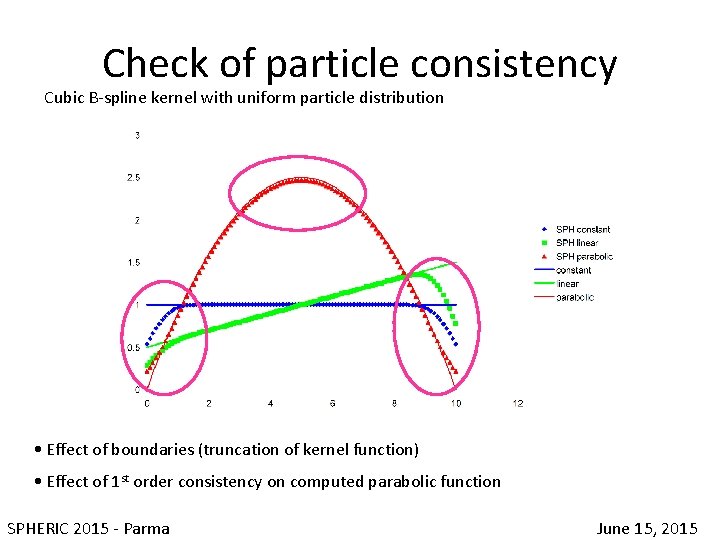
Check of particle consistency Cubic B-spline kernel with uniform particle distribution • Effect of boundaries (truncation of kernel function) • Effect of 1 st order consistency on computed parabolic function SPHERIC 2015 - Parma June 15, 2015

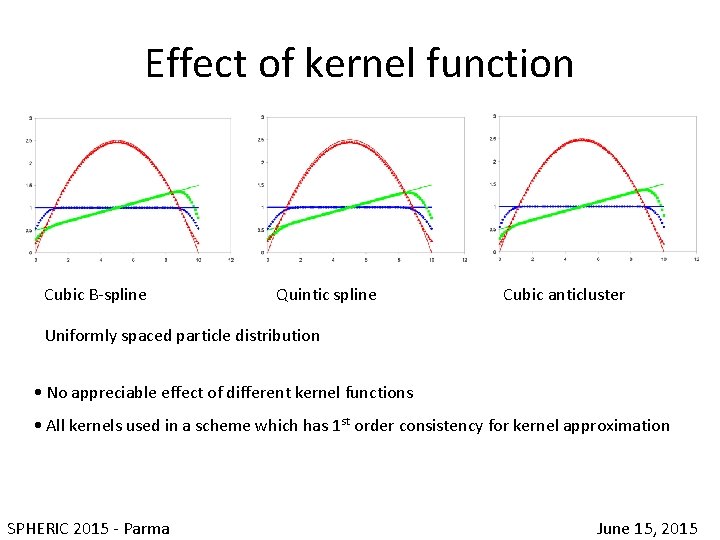
Effect of kernel function Cubic B-spline Quintic spline Cubic anticluster Uniformly spaced particle distribution • No appreciable effect of different kernel functions • All kernels used in a scheme which has 1 st order consistency for kernel approximation SPHERIC 2015 - Parma June 15, 2015

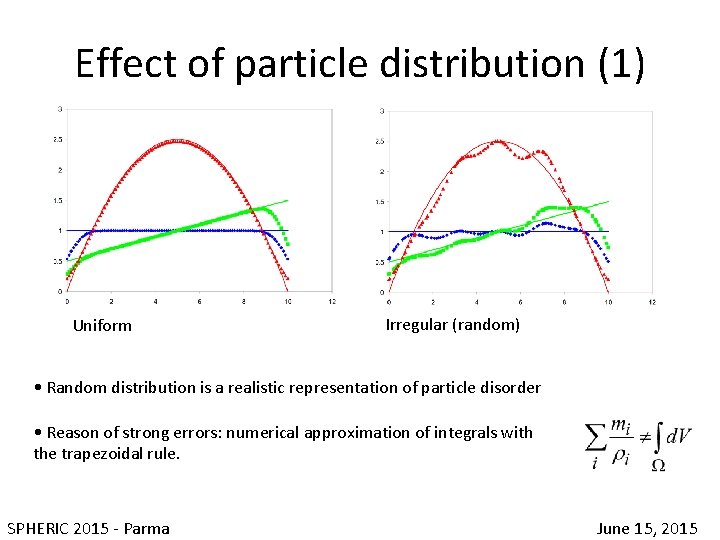
Effect of particle distribution (1) Uniform Irregular (random) • Random distribution is a realistic representation of particle disorder • Reason of strong errors: numerical approximation of integrals with the trapezoidal rule. SPHERIC 2015 - Parma June 15, 2015

Effect of particle distribution (2) Uniform Irregular (random) • Here the particle volume is computed exactly as the particle spacing Δx • Seems rather good… • Effect only on parabolic function reconstruction (owing to 1 st order consistency) SPHERIC 2015 - Parma June 15, 2015

Consistency of the first derivative f(x) = a f’(x) = 0 • Consistency of kernel approximation of gradient requires: • which implies: • 0 th order kernel consistency is guaranteed if the kernel is an even function (the gradient is an odd function). But… …particle approximation may not satisfy exactly the 0 th order consistency condition (near boundaries or for non-uniform particle distribution) SPHERIC 2015 - Parma June 15, 2015

Check of particle consistency Reproduction of the gradient of the constant, linear, quadratic function 1 D domain, length 10 h; kernel support: SPHERIC 2015 - Parma June 15, 2015

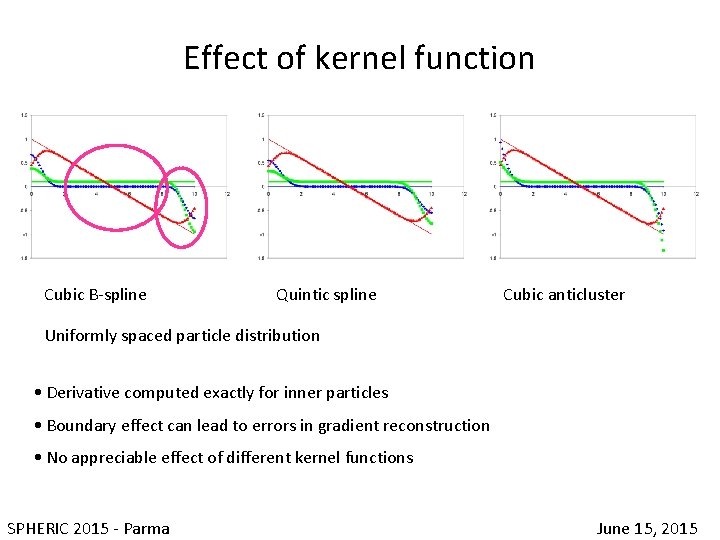
Effect of kernel function Cubic B-spline Quintic spline Cubic anticluster Uniformly spaced particle distribution • Derivative computed exactly for inner particles • Boundary effect can lead to errors in gradient reconstruction • No appreciable effect of different kernel functions SPHERIC 2015 - Parma June 15, 2015

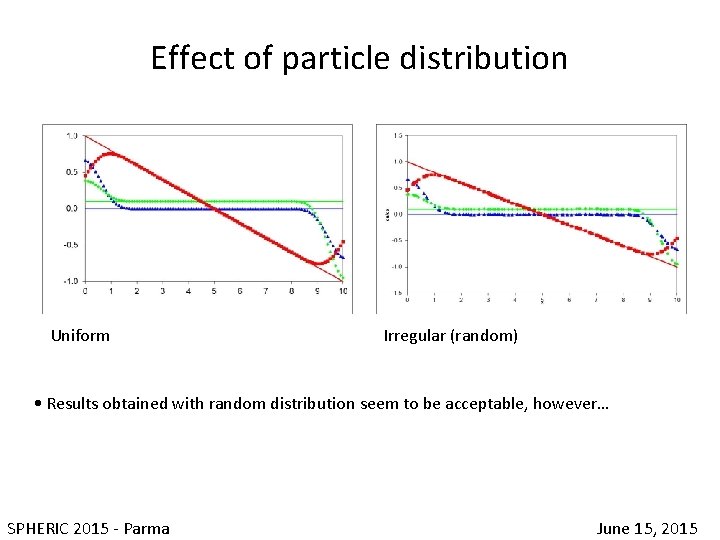
Effect of particle distribution Uniform Irregular (random) • Results obtained with random distribution seem to be acceptable, however… SPHERIC 2015 - Parma June 15, 2015

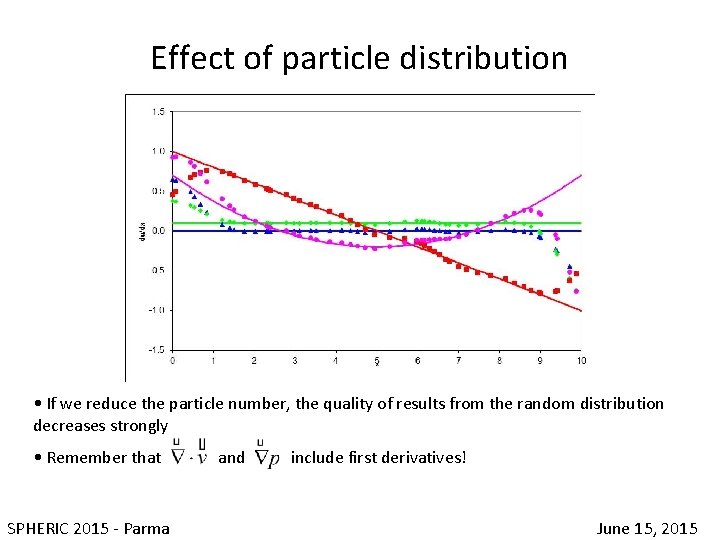
Effect of particle distribution • If we reduce the particle number, the quality of results from the random distribution decreases strongly • Remember that and include first derivatives! SPHERIC 2015 - Parma June 15, 2015

Consistency of the second derivative f(x) = a or f(x) = a x + b f’’(x) = 0 • Consistency of kernel approximation of derivatives requires: • which implies: • 0 th order consistency is again guaranteed if the kernel is an even function, because its second derivative is also an even function • However, consistency of the particle approximation is not guaranteed and sensitivity to particle disorder is high • Accuracy of second derivatives can be poorer than that of first derivatives even for uniform particle distributions SPHERIC 2015 - Parma June 15, 2015

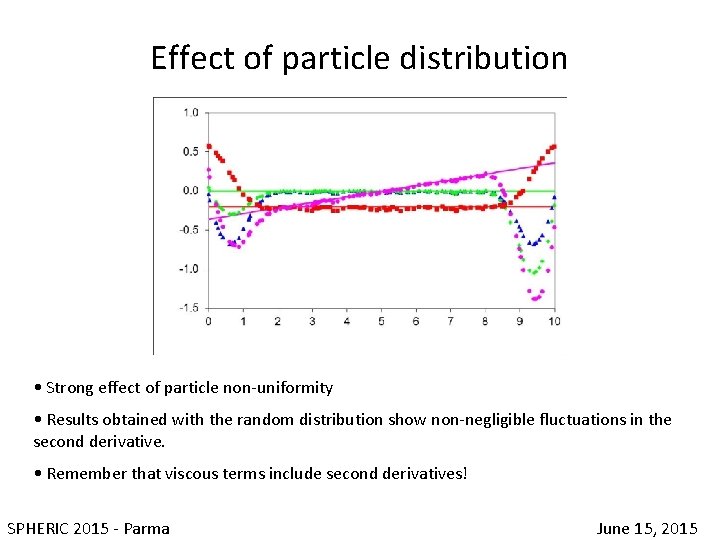
Effect of particle distribution • Strong effect of particle non-uniformity • Results obtained with the random distribution show non-negligible fluctuations in the second derivative. • Remember that viscous terms include second derivatives! SPHERIC 2015 - Parma June 15, 2015

Improved SPH consistency The function U can be expanded in Taylor series around xi: Multiplying by the kernel W and integrating over Ω we have: W even function SPHERIC 2015 - Parma June 15, 2015

Improved SPH consistency • Normalized kernel approximation: which restores 0 th order kernel consistency at the boundaries • Normalized particle approximation: (Shepard filtering) which restores 0 th order particle consistency also for non-uniform particle distributions

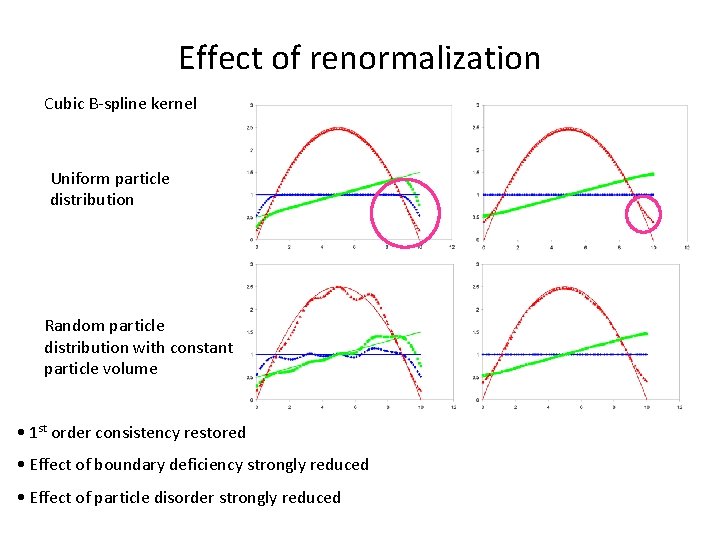
Effect of renormalization Cubic B-spline kernel Uniform particle distribution Random particle distribution with constant particle volume • 1 st order consistency restored • Effect of boundary deficiency strongly reduced • Effect of particle disorder strongly reduced

Improved consistency of 1 st derivative The kernel approximation of the Taylor expansion of U around xi can be multiplied by the x derivative of the kernel function, yielding: Truncated to 1 st order U(xi) known ∂U/ ∂x|xi unknown SPHERIC 2015 - Parma June 15, 2015

Improved consistency of 1 st derivative • Normalized 1 st derivative kernel approximation: which restores 1 st order kernel consistency at the boundaries • Normalized particle approximation: (Chen & Beraun, 2000) which restores 1 st order particle consistency also for non-uniform particle distributions

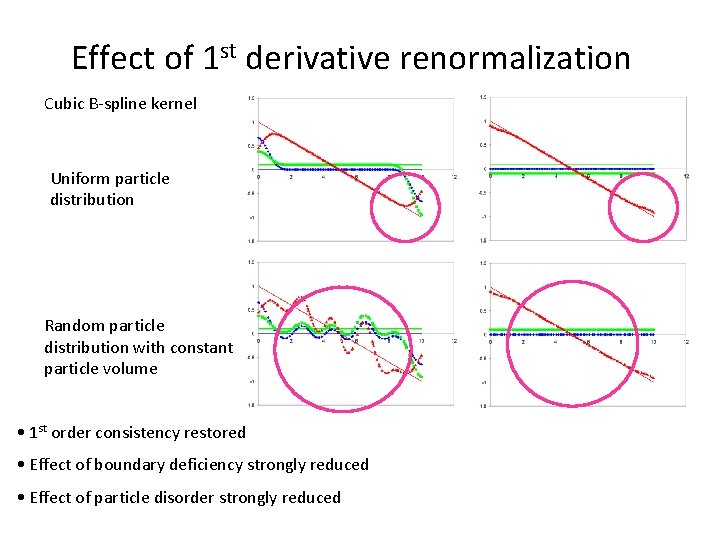
Effect of 1 st derivative renormalization Cubic B-spline kernel Uniform particle distribution Random particle distribution with constant particle volume • 1 st order consistency restored • Effect of boundary deficiency strongly reduced • Effect of particle disorder strongly reduced

Improved consistency of the gradient The function U can be expanded in Taylor series around xi: shifting to SPH interpolation with a convenient test function T and truncating to 1 st order, leads to: Which, using alternatively as T the kernel gradient components, yields the system: in the components of the gradient of U

Corrected kernel gradient • Alternative: use directly a corrected kernel gradient • Demonstration similar to the previous one (Bonet & Lok, 1999) SPHERIC 2015 - Parma June 15, 2015

Improved consistency of 2 nd derivative From the kernel approximation of the Taylor expansion of U around xi: Truncated to 2 nd order U(xi) and ∂U/ ∂x|xi known SPHERIC 2015 - Parma June 15, 2015

Improved consistency of 2 nd derivative one obtains: which restores 0 th order kernel consistency near the boundaries (the term only near boundaries) SPHERIC 2015 - Parma June 15, 2015

Improved consistency of 2 nd derivative The normalized particle approximation of the 2 nd derivative: where is the normalized first derivative already computed and 0 th order consistency is restored for a non-uniform particle distribution (Chen & Beraun, 2000) SPHERIC 2015 - Parma June 15, 2015

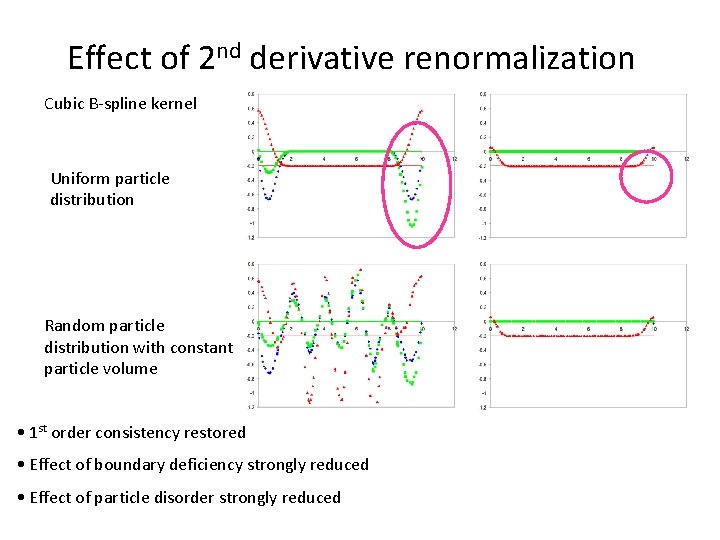
Effect of 2 nd derivative renormalization Cubic B-spline kernel Uniform particle distribution Random particle distribution with constant particle volume • 1 st order consistency restored • Effect of boundary deficiency strongly reduced • Effect of particle disorder strongly reduced

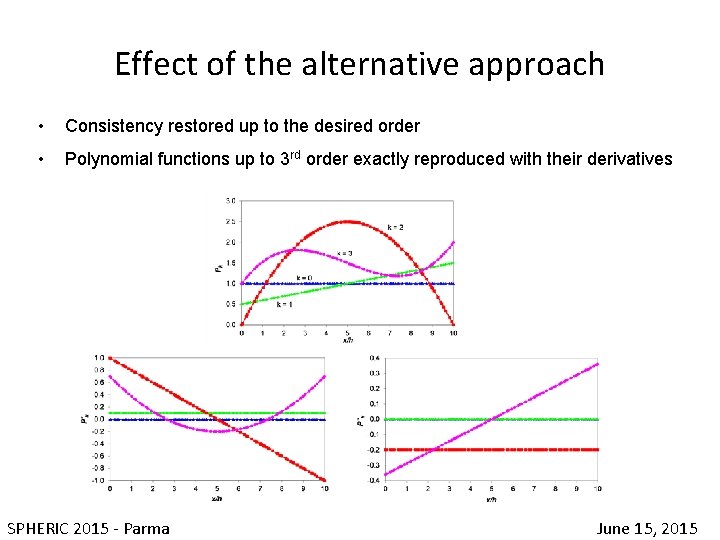
Alternative approach to restore consistency • Expand the function in Taylor series: • then derive the expansion, apply the particle approximation and solve simultaneously for the function and its gradient: (Liu & Liu, 2006) SPHERIC 2015 - Parma June 15, 2015

Alternative approach to restore consistency • the approach can be extended to higher-order derivatives (3 rd order consistency on the function, 2 nd order consistency on the first derivative) • it can become time-consuming when applied to 2 D and 3 D problems SPHERIC 2015 - Parma June 15, 2015

Effect of the alternative approach • Consistency restored up to the desired order • Polynomial functions up to 3 rd order exactly reproduced with their derivatives SPHERIC 2015 - Parma June 15, 2015

Navier-Stokes equations • Mass and momentum (and energy) conservation • Hydraulics: incompressible liquid, energy equation decoupled • SPH needs equations in Lagrangian form: SPHERIC 2015 - Parma June 15, 2015

Navier-Stokes equations • Explicit solution easier to handle (to manage particle displacement) • Two alternatives: • Projection methods (ISPH) • Artificial compressibility (WCSPH) • For artificial compressibility: Navier-Stokes equations for a Weakly Compressible fluid Small perturbations constant SPHERIC 2015 - Parma June 15, 2015

Navier-Stokes equations • Explicit solution easier to handle (to manage particle displacement) • Two alternatives: • Projection methods (ISPH) • Artificial compressibility (WCSPH) • For artificial compressibility: Navier-Stokes equations for a Weakly Compressible fluid Tait equation SPHERIC 2015 - Parma June 15, 2015

Continuity equation 3 alternatives have been devised to impose continuity : • compute the material derivative of density through an artificial compressibility model and obtain pressure through an equation of state for a weakly compressible liquid (WCSPH): • impose at each time step the SPH interpolation constraint on density (and, again, use an equation of state to obtain pressure) (WCSPH): • use projection methods and solve a Poisson equation for pressure (ISPH) SPHERIC 2015 - Parma June 15, 2015

Continuity equation • the continuity equation for compressible and weakly compressible flow (WCSPH) • becomes, in “plain” SPH form 2 h i j • however, in this form the divergence is not strictly zero for a constant field (at least, if no kernel gradient correction is performed) SPHERIC 2015 - Parma June 15, 2015

Continuity equation • the continuity equation can be suitably modified • being: • the following SPH approximation can be obtained: • which is also consistent with kernel gradient renormalization formulas SPHERIC 2015 - Parma June 15, 2015

Momentum equation • in the momentum equation • the pressure term becomes: • in this form, the action-reaction principle is not guaranteed (the force of i on j is not equal to the force of j on i) SPHERIC 2015 - Parma June 15, 2015

Momentum equation • the pressure term in the momentum equation can be suitably modified • being • the following SPH approximation can be obtained • which, however, conflicts with kernel gradient renormalization formulas… SPHERIC 2015 - Parma June 15, 2015

Viscous stress • the viscous stress term can be computed in its incompressible form • viscous stress can be computed by applying the second derivative directly to the kernel function • however, the “plain” approximation is not used in practice as we have seen that it can be too sensitive to particle disorder • for constant viscosity, we can also use renormalized second derivatives SPHERIC 2015 - Parma June 15, 2015

Viscous stress • alternatively, viscous stress can be computed by direct estimation of the velocity gradient • and, being: • the following SPH approximation can be obtained • which can be directly applied also to non-Newtonian fluids and/or turbulent flows SPHERIC 2015 - Parma June 15, 2015

Viscous stress • alternatively, expanding the velocity around point xi: • rearranging: • the following SPH approximation can be obtained • used also to build artificial viscosity terms (Monaghan) SPHERIC 2015 - Parma June 15, 2015

Artificial viscosity • developed by Monaghan to avoid instabilities in shock waves and to prevent interpenetration of particles • it is introduced only when i j • the artificial kinematic viscosity coefficient is proportional to • the term to be added to the Navier-Stokes equations is: • a is known as Monaghan’s viscosity coefficient SPHERIC 2015 - Parma June 15, 2015

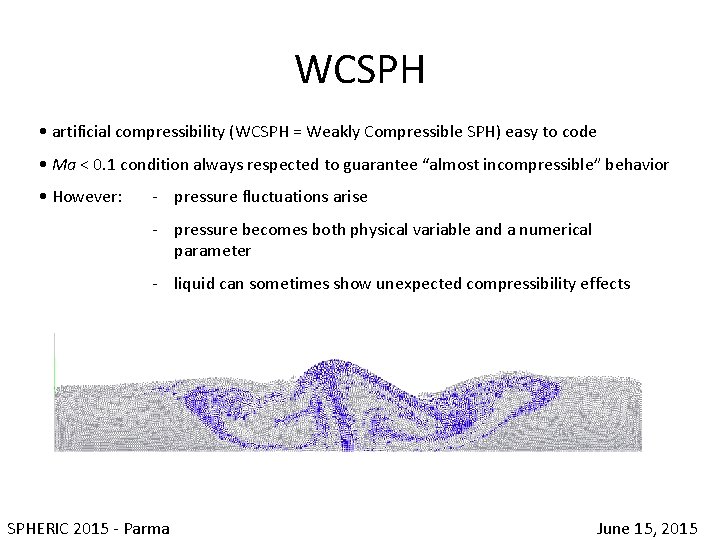
WCSPH • artificial compressibility (WCSPH = Weakly Compressible SPH) easy to code • Ma < 0. 1 condition always respected to guarantee “almost incompressible” behavior • However: - pressure fluctuations arise - pressure becomes both physical variable and a numerical parameter - liquid can sometimes show unexpected compressibility effects SPHERIC 2015 - Parma June 15, 2015

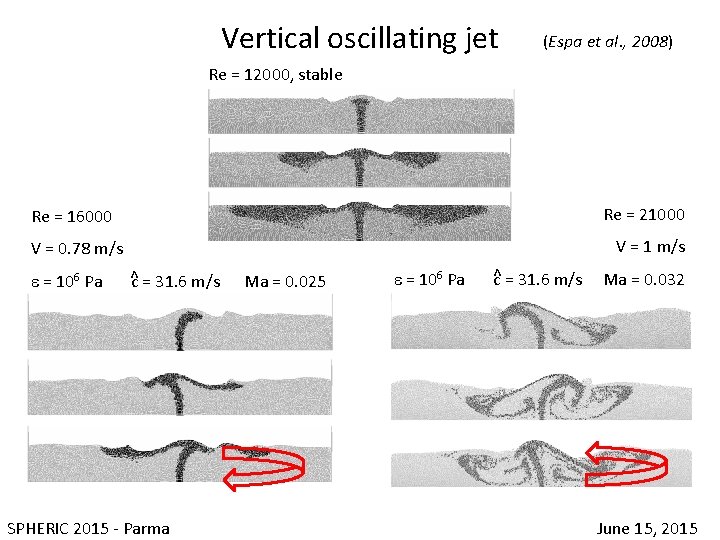
Vertical oscillating jet (Espa et al. , 2008) Re = 12000, stable Re = 16000 V = 0. 78 m/s ^ e = 106 Pa c = 31. 6 m/s Ma = 0. 025 Re = 21000 V = 1 m/s ^ e = 106 Pa c = 31. 6 m/s Ma = 0. 032 SPHERIC 2015 - Parma June 15, 2015

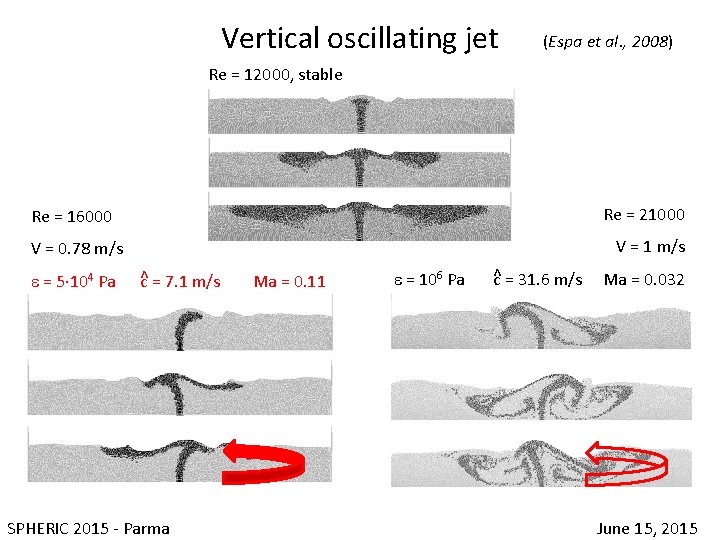
Vertical oscillating jet (Espa et al. , 2008) Re = 12000, stable Re = 16000 V = 0. 78 m/s ^ e = 5· 104 Pa c = 7. 1 m/s Ma = 0. 11 Re = 21000 V = 1 m/s ^ e = 106 Pa c = 31. 6 m/s Ma = 0. 032 SPHERIC 2015 - Parma June 15, 2015

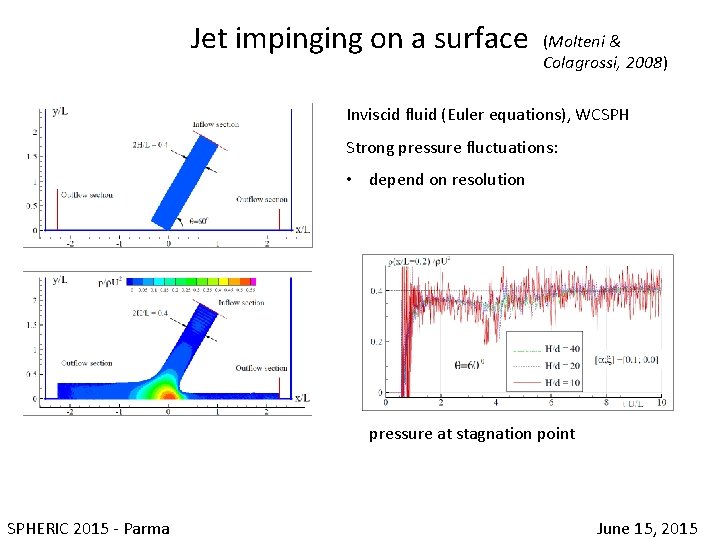
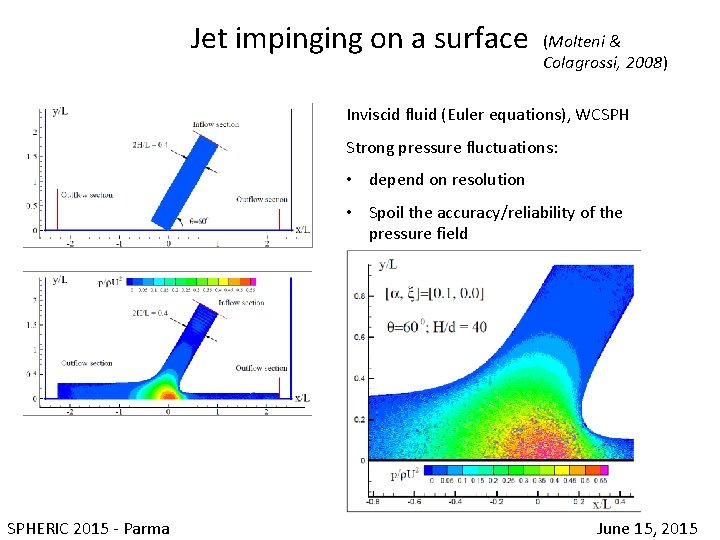
Jet impinging on a surface (Molteni & Colagrossi, 2008) Inviscid fluid (Euler equations), WCSPH Strong pressure fluctuations: • depend on resolution pressure at stagnation point SPHERIC 2015 - Parma June 15, 2015

Jet impinging on a surface (Molteni & Colagrossi, 2008) Inviscid fluid (Euler equations), WCSPH Strong pressure fluctuations: • depend on resolution • Spoil the accuracy/reliability of the pressure field SPHERIC 2015 - Parma June 15, 2015

WCSPH correction techniques • pressure (or density) smoothing • Density diffusion term in the continuity equation (d-SPH): SPHERIC 2015 - Parma June 15, 2015

ISPH • an alternative to artificial compressibility is the SPH form of a projection method • classical projection method by Chorin, applied to SPH: SPHERIC 2015 - Parma June 15, 2015

ISPH • in the SPH formalism: • linear system with sparse coefficient matrix • proper boundary conditions • corrected values for velocity and position: SPHERIC 2015 - Parma June 15, 2015

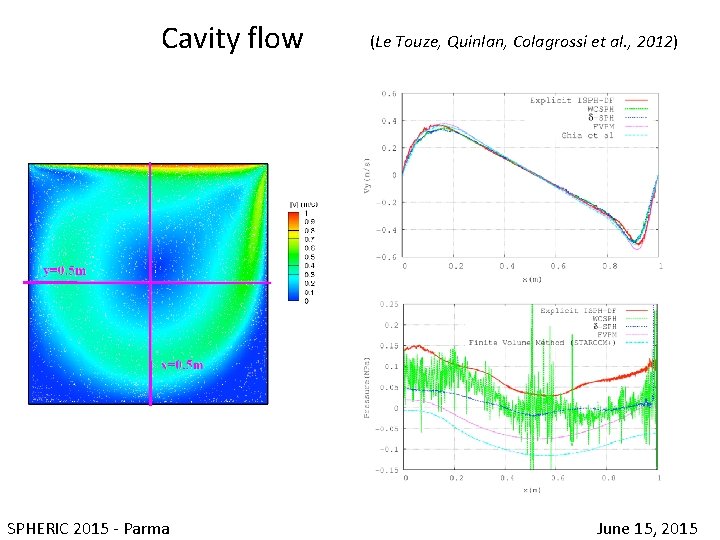
Cavity flow (Le Touze, Quinlan, Colagrossi et al. , 2012) SPHERIC 2015 - Parma June 15, 2015

Neighbour search • needed at each time step to determine links between particles • several strategies: e. g. linked list 1) determine the limits of space occupied by particles Vajont landslide (Manenti et al. , 2014) SPHERIC 2015 - Parma June 15, 2015

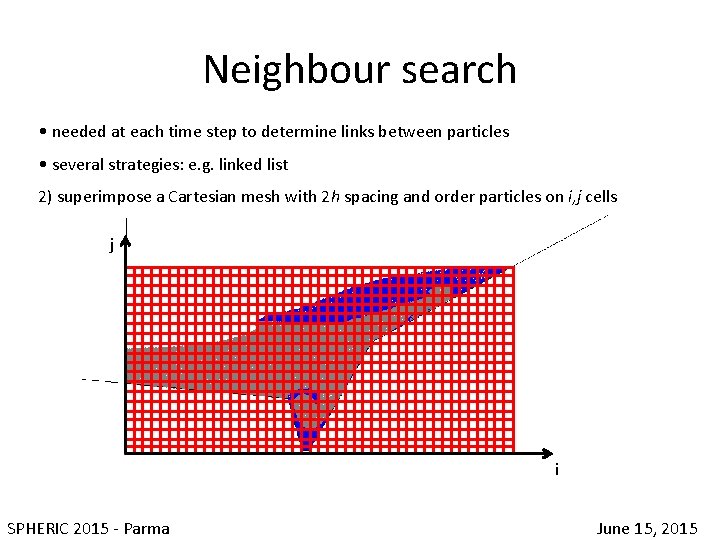
Neighbour search • needed at each time step to determine links between particles • several strategies: e. g. linked list 2) superimpose a Cartesian mesh with 2 h spacing and order particles on i, j cells j i SPHERIC 2015 - Parma June 15, 2015

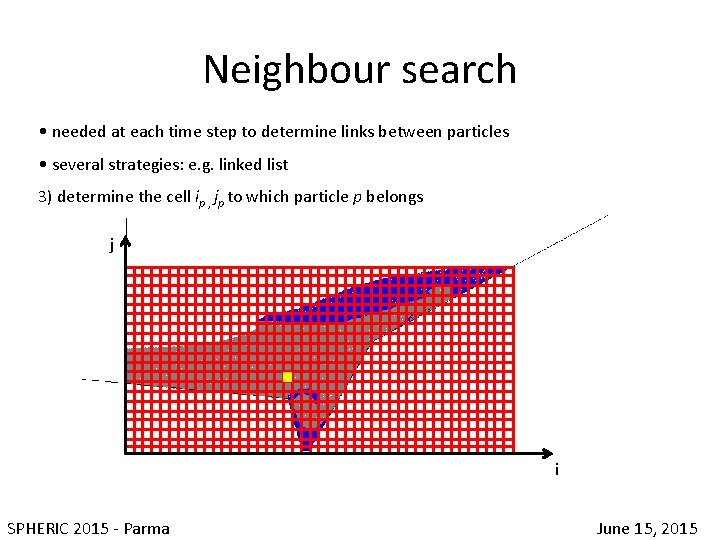
Neighbour search • needed at each time step to determine links between particles • several strategies: e. g. linked list 3) determine the cell ip , jp to which particle p belongs j i SPHERIC 2015 - Parma June 15, 2015

Neighbour search • needed at each time step to determine links between particles • several strategies: e. g. linked list 4) Compute particle distances from p only in the cells with ip-1 < ip+1 and jp-1 < jp+1 j i SPHERIC 2015 - Parma June 15, 2015

Time integration • various approaches have been developed for the integration of the ODEs in time which result from SPH discretization • explicit: • semi-implicit: Courant condition SPHERIC 2015 - Parma June 15, 2015

Time integration • predictor-corrector (Monaghan’s reversible scheme): • Runge-Kutta methods • … SPHERIC 2015 - Parma June 15, 2015

XSPH • • Explicit solution of momentum equation Velocity correction • • Corrected values used in particle motion Uncorrected values used in continuity equation and for stress evaluation SPHERIC 2015 - Parma June 15, 2015

Boundary conditions • Assigned conditions need to be enforced at boundaries to ensure correct physical conditions to the required flow: • wall boundary conditions to velocity and density (pressure) • inflow and outflow conditions according to physics • free surface conditions (only to pressure in ISPH) • Interface conditions (for multiphase flow or fluid-structure interaction) • Further numerical reasons: • to guarantee full coverage of kernel support at boundaries (if no accurate kernel gradient correction is employed) • to prevent wall boundaries from particle penetration (not excluded a priori with explicit methods) SPHERIC 2015 - Parma June 15, 2015

Ghost particles (Randles & Libersky , 1996) • particle position is mirrored from the flow to an external fictitious layer • velocity: slip condition 2 h or no slip condition • pressure/density/stress tensor: Neumann condition i g j • solution of momentum and continuity equations includes boundary particles SPHERIC 2015 - Parma June 15, 2015

Ghost particles • Advantages: • easy to code for plane boundaries • rather computationally efficient 2 h i g j • prevents efficiently particle penetration • restores consistency at boundaries • Drawbacks: • curved boundaries generate coarser/finer particle distribution • corners generate duplication of ghost particles ? g 2 h i g’ j SPHERIC 2015 - Parma June 15, 2015

Ghost particles • Improvement: • local planar approximation of the boundary • ghost particle extrapolation in the “empty” kernel support of each inner particle • make use of virtual particles to define boundary and locate ghost particles (VBM) 2 h g i j • more computationally expensive • can restore consistency at boundaries to the desired order SPHERIC 2015 - Parma June 15, 2015

Fixed boundary particles • fixed “ghost” particles • values in particle b based on SPH interpolation in mirror point p 2 h b p • fixes some “geometrical” drawbacks of ghost particle method j SPHERIC 2015 - Parma June 15, 2015

Fixed boundary particles • barrier particles • located directly on the boundary • apply a normal repulsive force on the inner particles 2 h • analogous to Lennard-Jones potential in molecular interaction • not completely physically-based j SPHERIC 2015 - Parma June 15, 2015

Boundary integrals • the particle approximation can be split in a flow (F) and boundary (B) contribution • the term related to the boundary can be computed analytically from the kernel / kernel gradient function b 2 h B F i a j • e. g. continuity equation: SPHERIC 2015 - Parma June 15, 2015

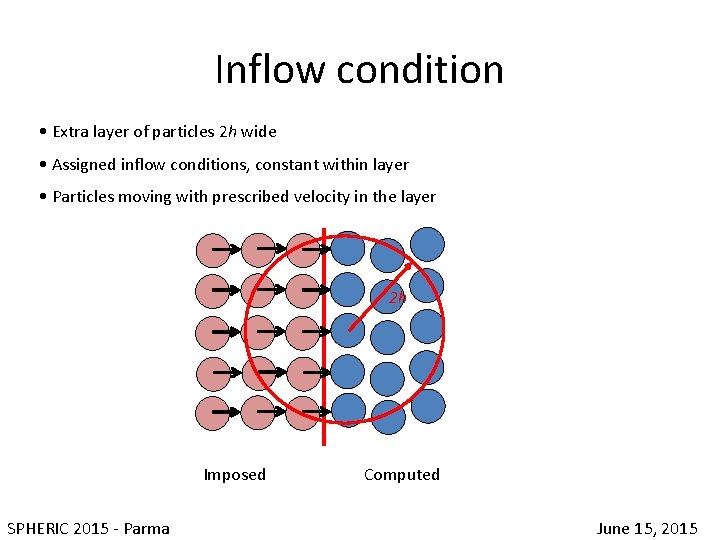
Inflow condition • Extra layer of particles 2 h wide • Assigned inflow conditions, constant within layer • Particles moving with prescribed velocity in the layer 2 h Imposed Computed SPHERIC 2015 - Parma June 15, 2015

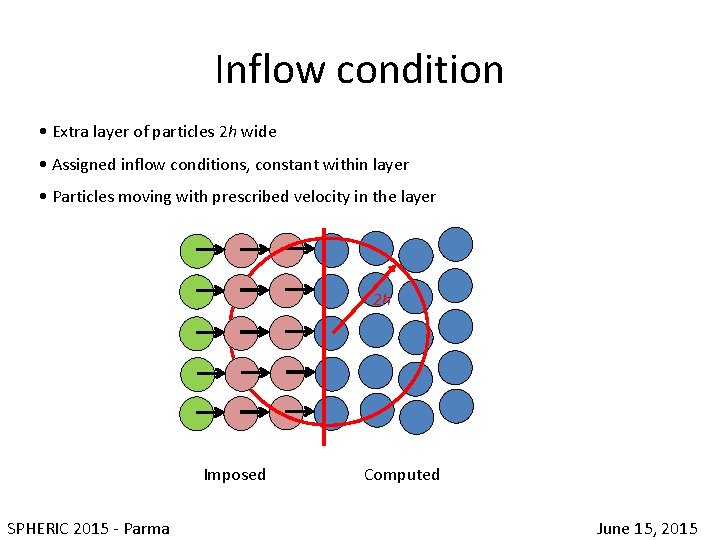
Inflow condition • Extra layer of particles 2 h wide • Assigned inflow conditions, constant within layer • Particles moving with prescribed velocity in the layer 2 h Imposed Computed SPHERIC 2015 - Parma June 15, 2015

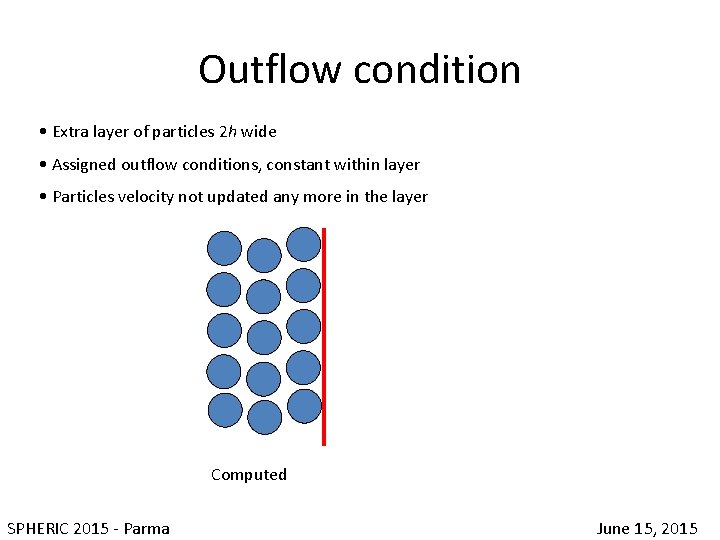
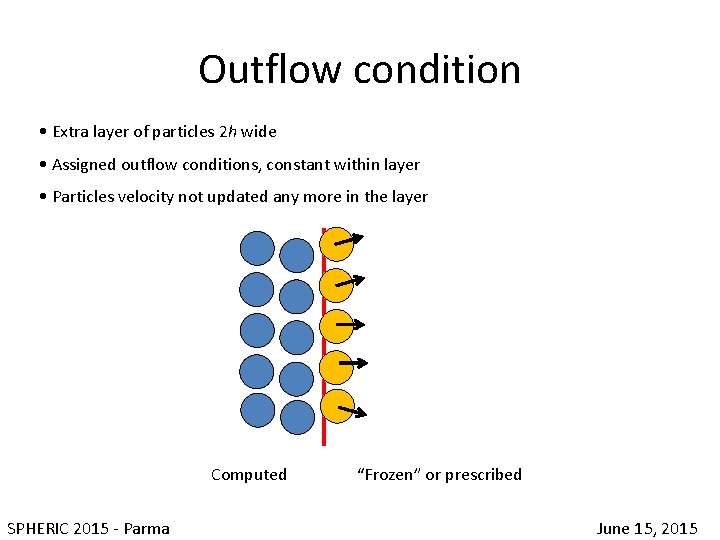
Outflow condition • Extra layer of particles 2 h wide • Assigned outflow conditions, constant within layer • Particles velocity not updated any more in the layer Computed SPHERIC 2015 - Parma June 15, 2015

Outflow condition • Extra layer of particles 2 h wide • Assigned outflow conditions, constant within layer • Particles velocity not updated any more in the layer Computed “Frozen” or prescribed SPHERIC 2015 - Parma June 15, 2015

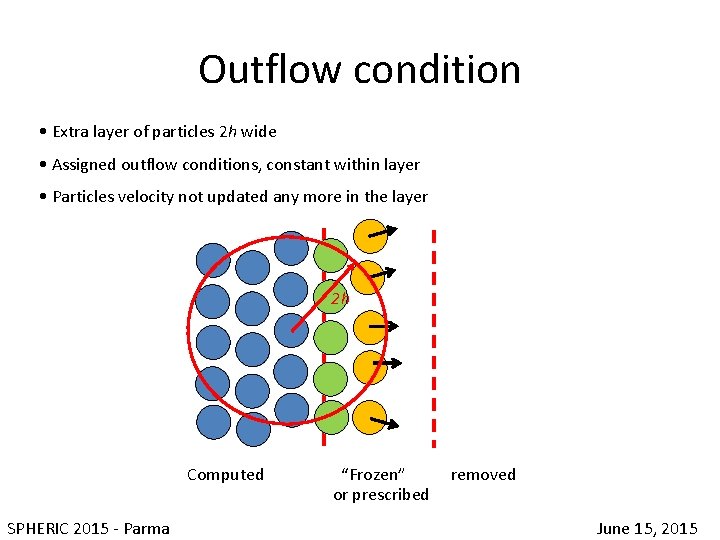
Outflow condition • Extra layer of particles 2 h wide • Assigned outflow conditions, constant within layer • Particles velocity not updated any more in the layer 2 h Computed “Frozen” removed or prescribed SPHERIC 2015 - Parma June 15, 2015

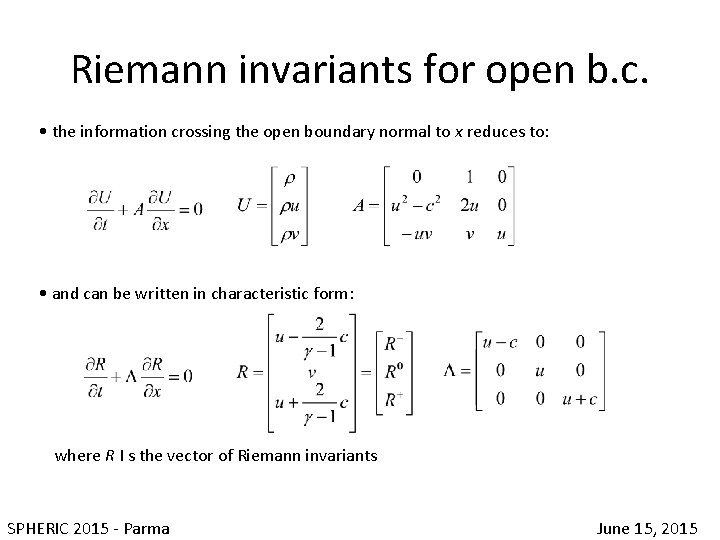
Riemann invariants for open b. c. • boundary values can be assigned directly or, more physically, according to wave propagation in the weakly compressible flow • simplified case: • 2 D Euler equations • open boundaries normal to x being: g = 7 SPHERIC 2015 - Parma June 15, 2015

Riemann invariants for open b. c. • the information crossing the open boundary normal to x reduces to: • and can be written in characteristic form: where R I s the vector of Riemann invariants SPHERIC 2015 - Parma June 15, 2015

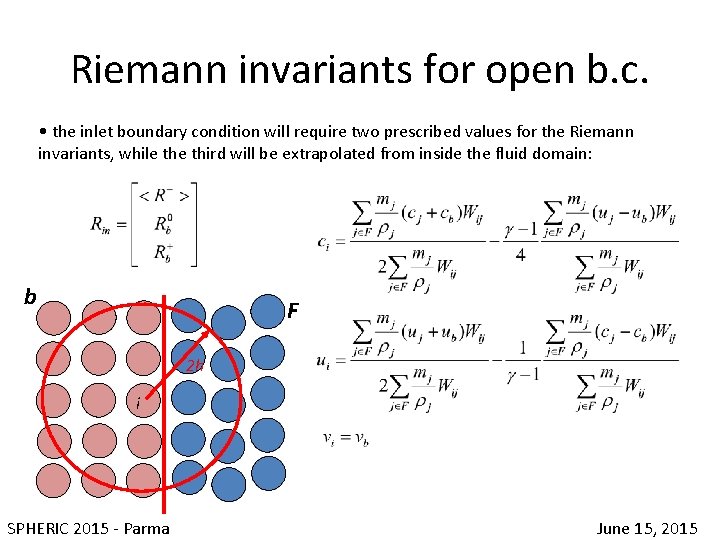
Riemann invariants for open b. c. • the inlet boundary condition will require two prescribed values for the Riemann invariants, while third will be extrapolated from inside the fluid domain: b F 2 h i SPHERIC 2015 - Parma June 15, 2015

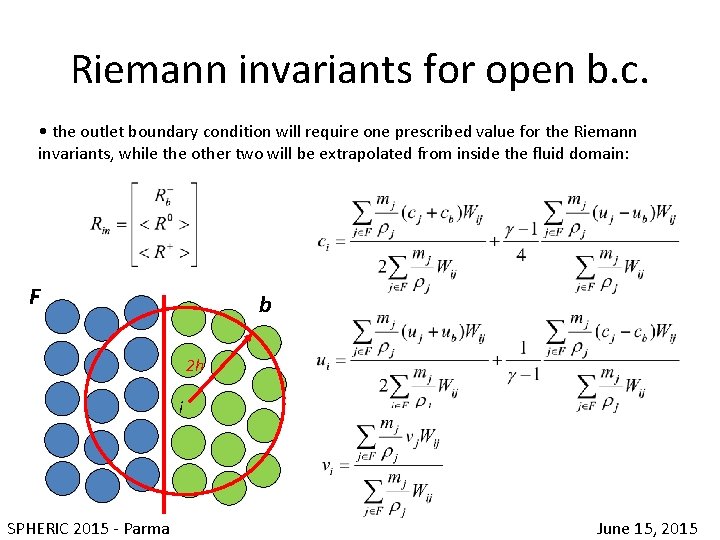
Riemann invariants for open b. c. • the outlet boundary condition will require one prescribed value for the Riemann invariants, while the other two will be extrapolated from inside the fluid domain: F b 2 h i SPHERIC 2015 - Parma June 15, 2015