Speeding up LDA 1 The LDA Topic Model

Speeding up LDA 1

The LDA Topic Model 2

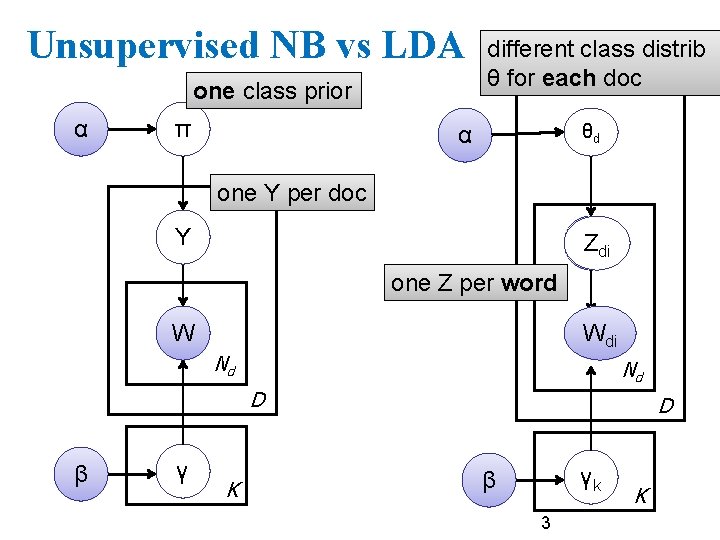
Unsupervised NB vs LDA one class prior α π different class distrib θ for each doc θd α one Y per doc Y Y Zdi one Z per word W Wdi Nd Nd D β γ K D γk β 3 K

• LDA’s view of a document Mixed membership model 4

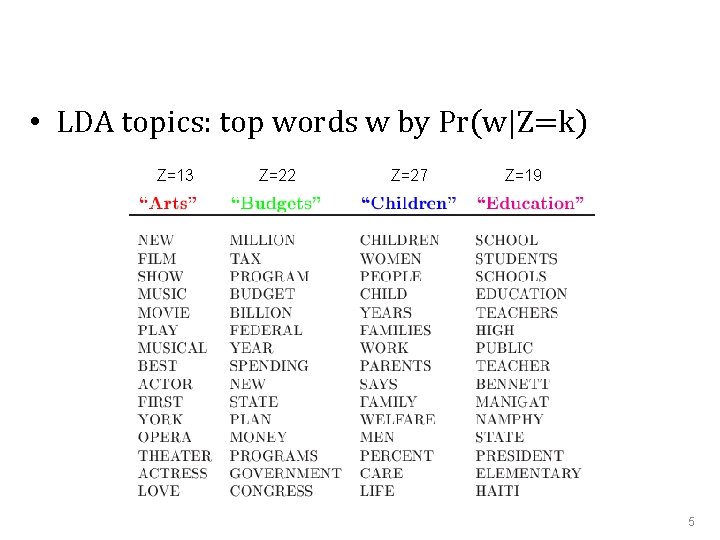
• LDA topics: top words w by Pr(w|Z=k) Z=13 Z=22 Z=27 Z=19 5

Parallel LDA 6

JMLR 2009 7

Observation • How much does the choice of z depend on the other z’s in the same document? – quite a lot • How much does the choice of z depend on the other z’s in elsewhere in the corpus? – maybe not so much – depends on Pr(w|t) but that changes slowly • Can we parallelize Gibbs and still get good results? 8

Question • Can we parallelize Gibbs sampling? – formally, no: every choice of z depends on all the other z’s – Gibbs needs to be sequential • just like SGD 9

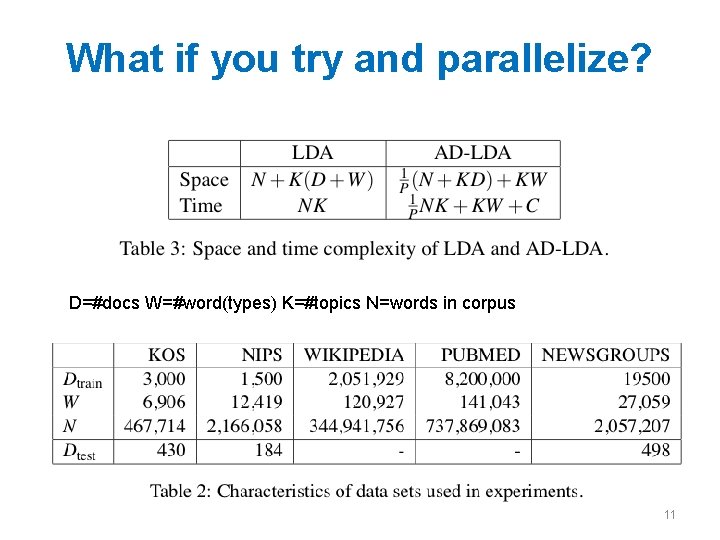
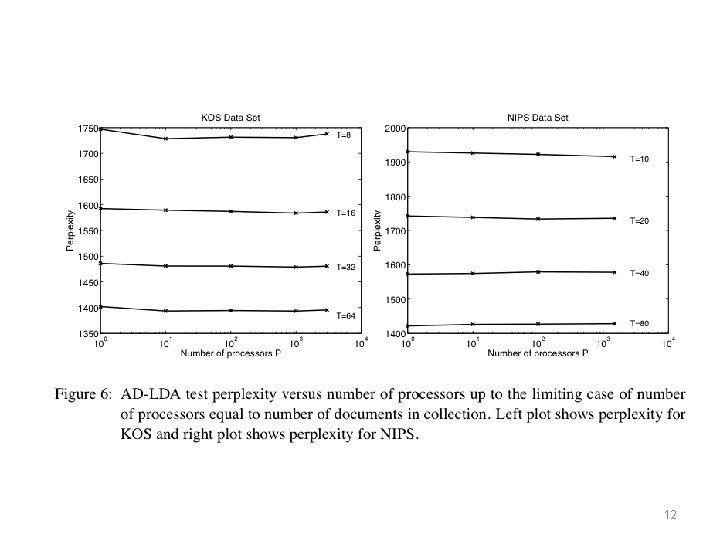
What if you try and parallelize? Split document/term matrix randomly and distribute to p processors. . then run “Approximate Distributed LDA” 10

What if you try and parallelize? D=#docs W=#word(types) K=#topics N=words in corpus 11

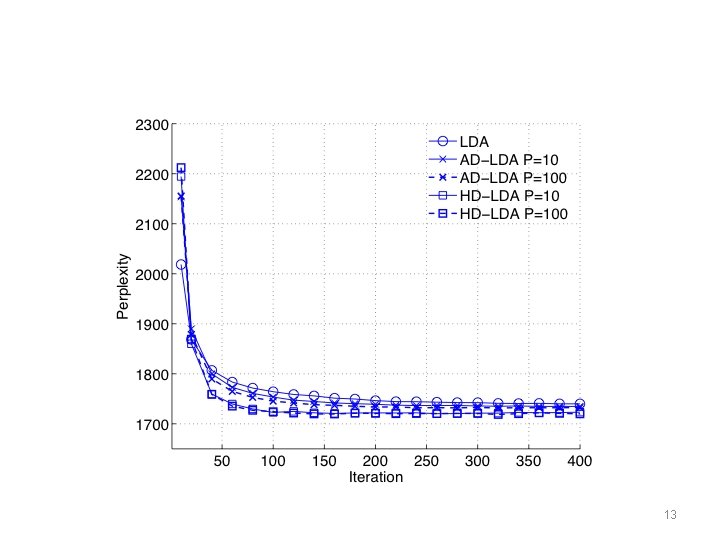
12

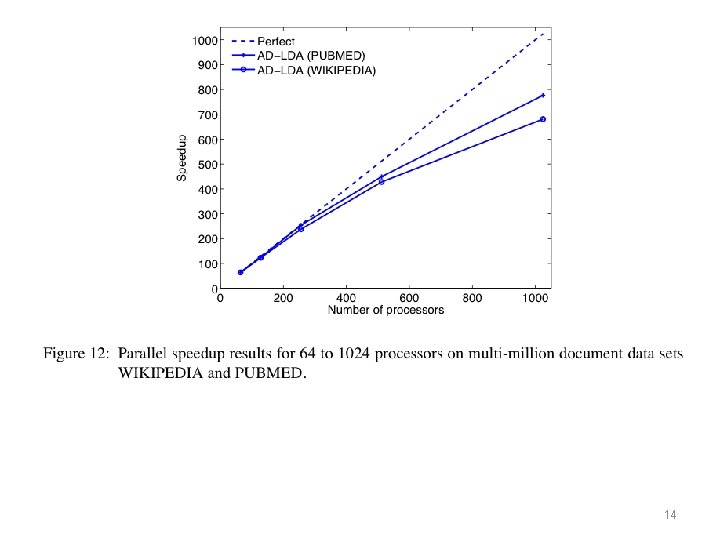
13

14

Update c. 2014 • Algorithms: – Distributed variational EM – Asynchronous LDA (AS-LDA) – Approximate Distributed LDA (AD-LDA) – Ensemble versions of LDA: HLDA, DCM-LDA • Implementations: – Git. Hub Yahoo_LDA • not Hadoop, special-purpose communication code for synchronizing the global counts • Alex Smola, Yahoo CMU – Mahout LDA • Andy Schlaikjer, CMU Twitter 15

Faster Sampling for LDA 16

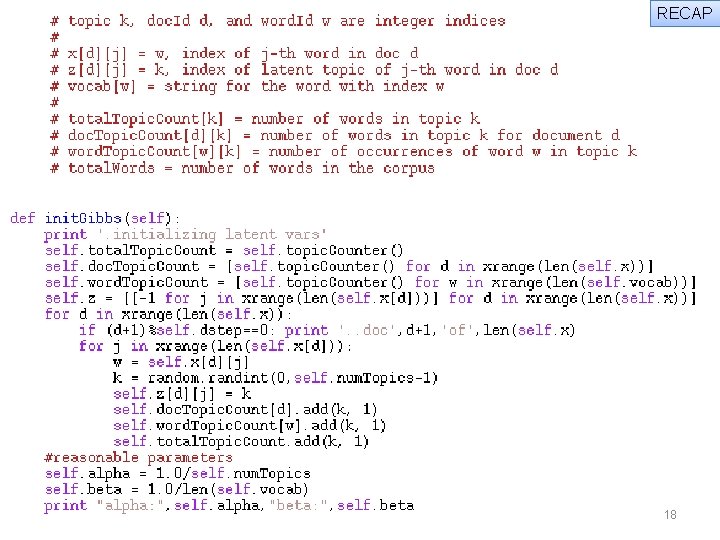
RECAP Way way more detail 17

RECAP More detail 18

RECAP 19

RECAP 20

RECAP z=1 random z=2 z=3 unit height … … 1. You spend a lot of time sampling 2. There’s a loop over all topics here in the sampler 21

KDD 09 22

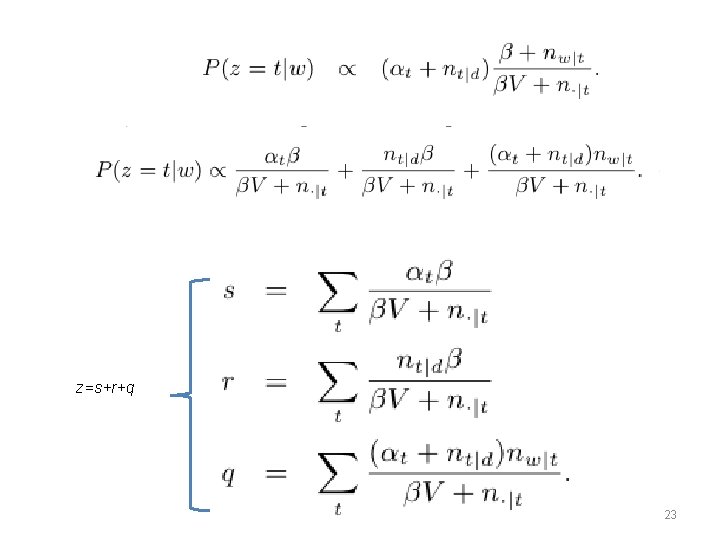
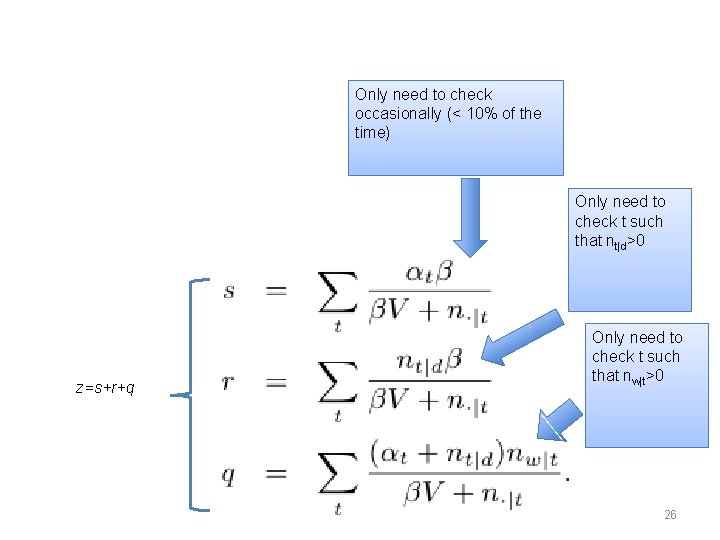
z=s+r+q 23

• If U<s: • lookup U on line segment with ticmarks at α 1β/(βV + n. |1), α 2β/(βV + n. |2), … Only need to • If s<U<r: check t such that n >0 • lookup U on line segment for r t|d z=s+r+q 24

• If U<s: • lookup U on line segment with ticmarks at α 1β/(βV + n. |1), α 2β/(βV + n. |2), … • If s<U<s+r: • lookup U on line segment for r • If s+r<U: Only need to • lookup U on line segment for q check t such z=s+r+q that nw|t>0 25

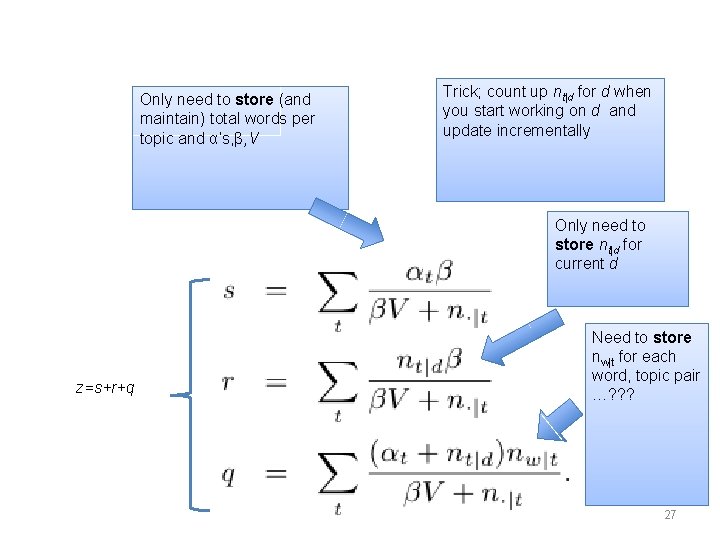
Only need to check occasionally (< 10% of the time) Only need to check t such that nt|d>0 z=s+r+q Only need to check t such that nw|t>0 26

Only need to store (and maintain) total words per topic and α’s, β, V Trick; count up nt|d for d when you start working on d and update incrementally Only need to store nt|d for current d z=s+r+q Need to store nw|t for each word, topic pair …? ? ? 27

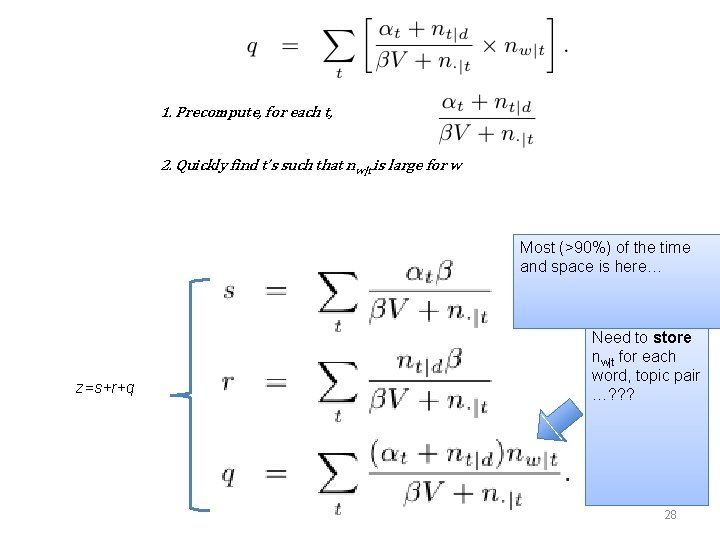
1. Precompute, for each t, 2. Quickly find t’s such that nw|t is large for w Most (>90%) of the time and space is here… z=s+r+q Need to store nw|t for each word, topic pair …? ? ? 28

1. Precompute, for each t, 2. Quickly find t’s such that nw|t is large for w • • • map w to an int array • no larger than frequency w • no larger than #topics encode (t, n) as a bit vector • n in the high-order bits • t in the low-order bits keep ints sorted in descending order Most (>90%) of the time and space is here… Need to store nw|t for each word, topic pair …? ? ? 29

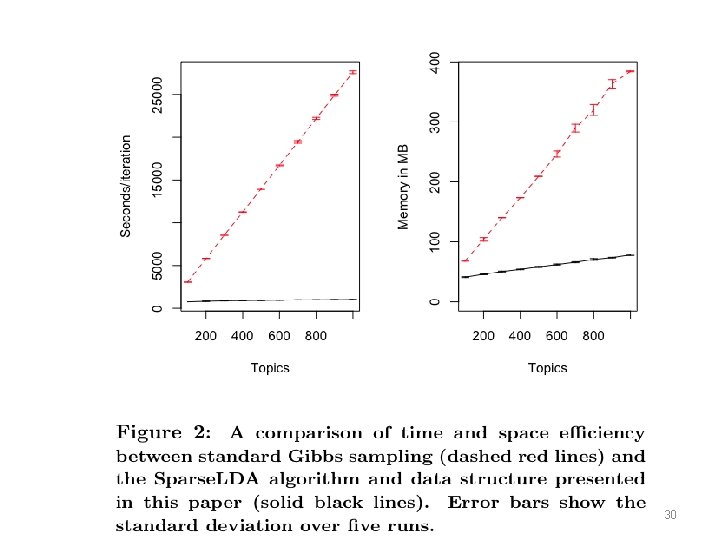
30

Other Fast Samplers for LDA 31

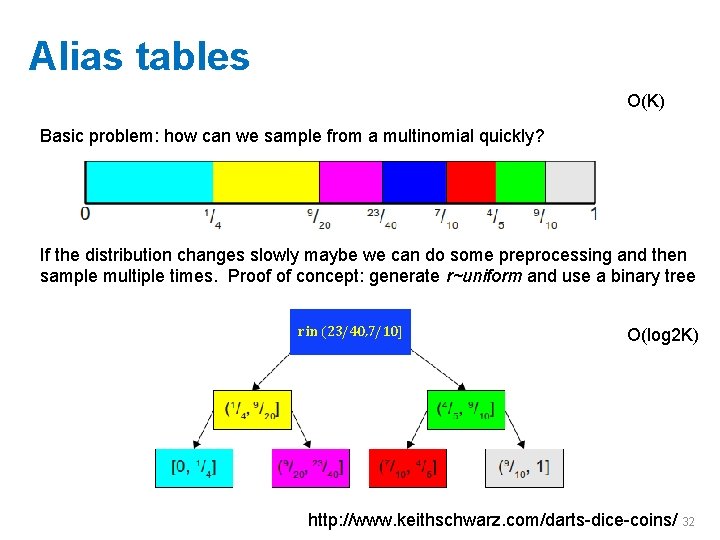
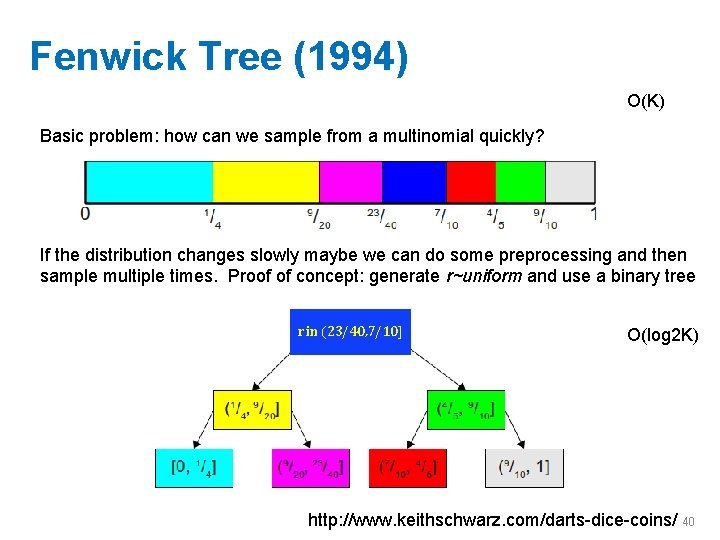
Alias tables O(K) Basic problem: how can we sample from a multinomial quickly? If the distribution changes slowly maybe we can do some preprocessing and then sample multiple times. Proof of concept: generate r~uniform and use a binary tree r in (23/40, 7/10] O(log 2 K) http: //www. keithschwarz. com/darts-dice-coins/ 32

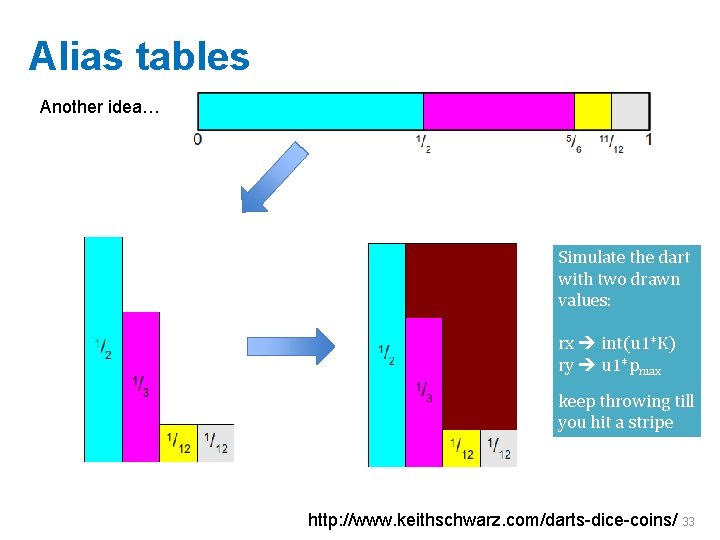
Alias tables Another idea… Simulate the dart with two drawn values: rx int(u 1*K) ry u 1*pmax keep throwing till you hit a stripe http: //www. keithschwarz. com/darts-dice-coins/ 33

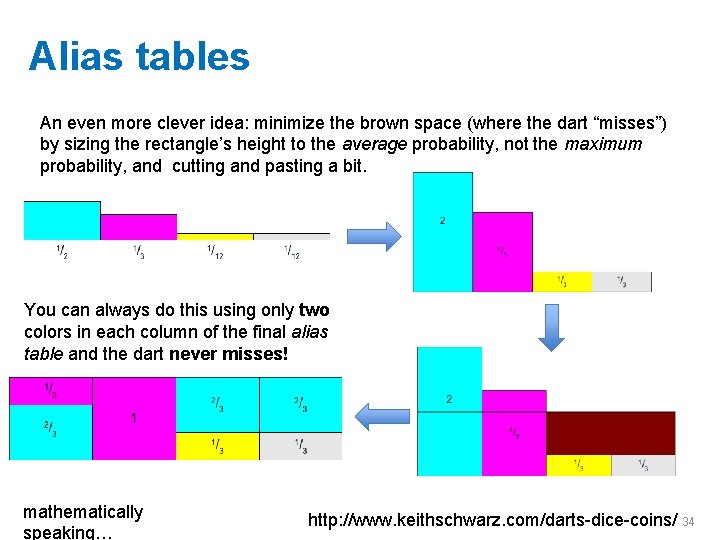
Alias tables An even more clever idea: minimize the brown space (where the dart “misses”) by sizing the rectangle’s height to the average probability, not the maximum probability, and cutting and pasting a bit. You can always do this using only two colors in each column of the final alias table and the dart never misses! mathematically speaking… http: //www. keithschwarz. com/darts-dice-coins/ 34

Alias sampling for LDA • You can sample quickly…. – But you need to regenerate the alias table after every topic switch • Workaround: – Sample from an old, stale alias table – Update it periodically – Compensate for the stale parameters by replacing Gibbs sampling with Metropolis. Hastings (MH) 35

Alias sampling for LDA • MH sampler: q defined by stale alias sampler we can sample quickly and easily from q we can evaluate p(i) easily p is based on actual counts here i and j are vectors of topic assignments 36

37

Yet More Fast Samplers for LDA 38

39

Fenwick Tree (1994) O(K) Basic problem: how can we sample from a multinomial quickly? If the distribution changes slowly maybe we can do some preprocessing and then sample multiple times. Proof of concept: generate r~uniform and use a binary tree r in (23/40, 7/10] O(log 2 K) http: //www. keithschwarz. com/darts-dice-coins/ 40

Data structures and algorithms LSearch: linear search 41

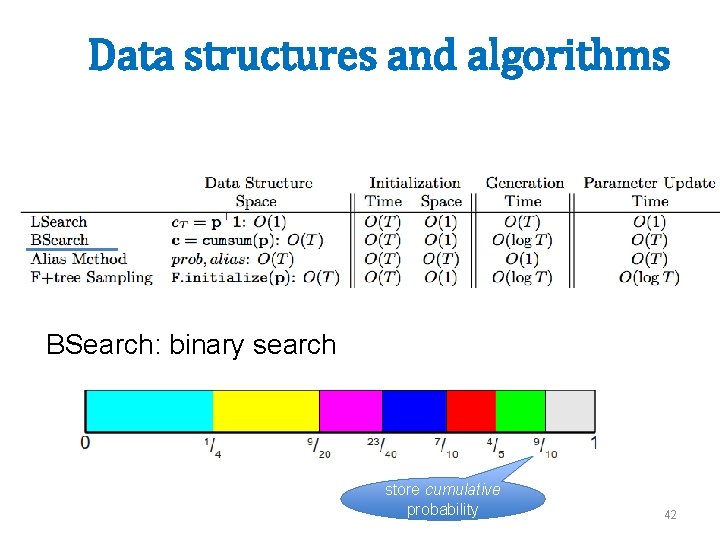
Data structures and algorithms BSearch: binary search store cumulative probability 42

Data structures and algorithms Alias sampling…. . 43

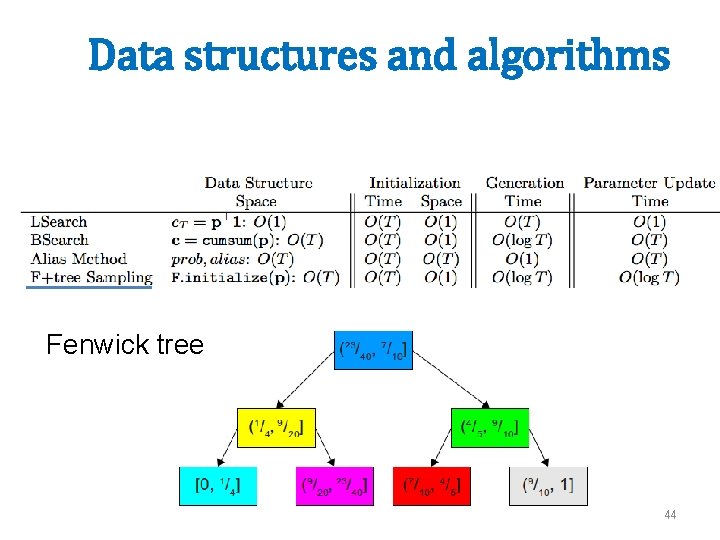
Data structures and algorithms Fenwick tree 44

Data structures and algorithms Fenwick tree βq: dense, changes slowly, re-used for each word in a document Binary search r: sparse, a different one is needed for each uniq term in doc Sampler is: 45

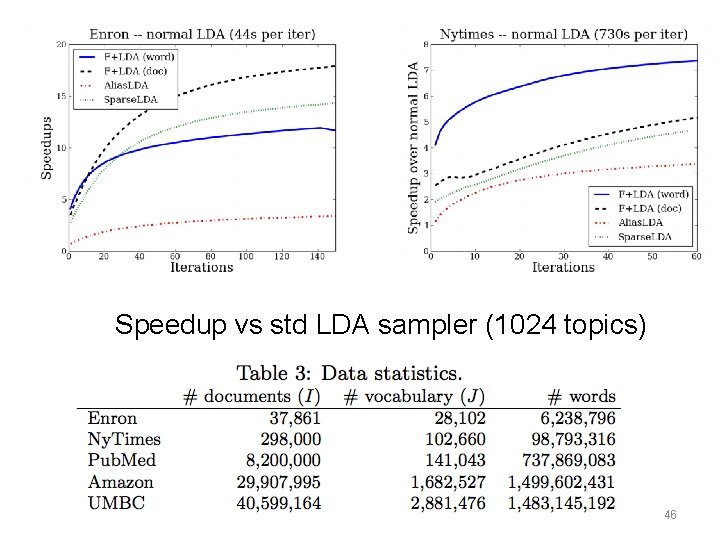
Speedup vs std LDA sampler (1024 topics) 46

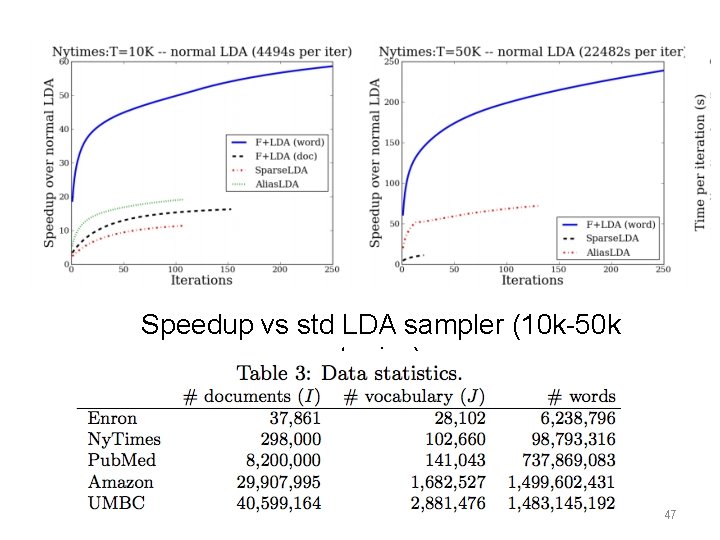
Speedup vs std LDA sampler (10 k-50 k topics) 47

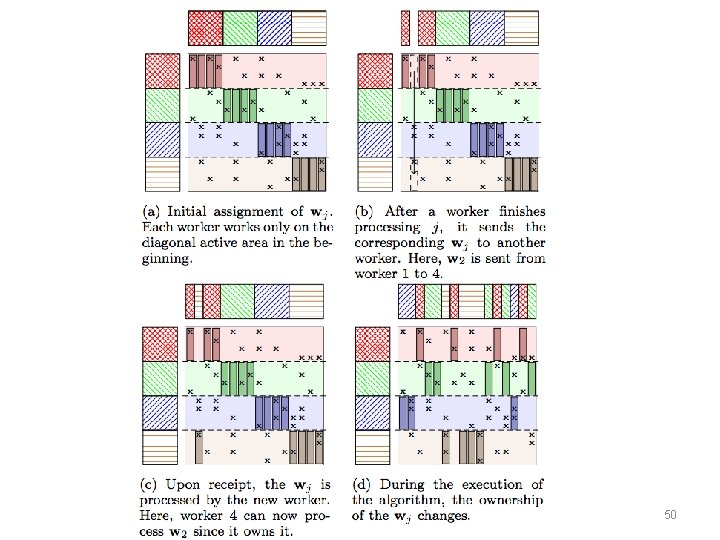
And Parallelism…. 48

Second idea: you can sample document-by-document or word-byword …. or…. use a MF-like approach to distributing the data. 49

50

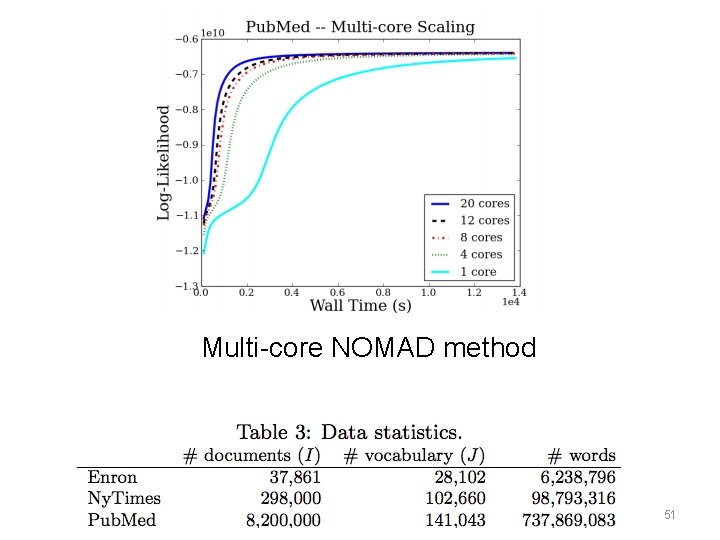
Multi-core NOMAD method 51

On Beyond LDA 52

Network Datasets • UBMCBlog • AGBlog • MSPBlog • Cora • Citeseer 53

Motivation • Social graphs seem to have – some aspects of randomness • small diameter, giant connected components, . . – some structure • homophily, scale-free degree dist? • How do you model it? 54

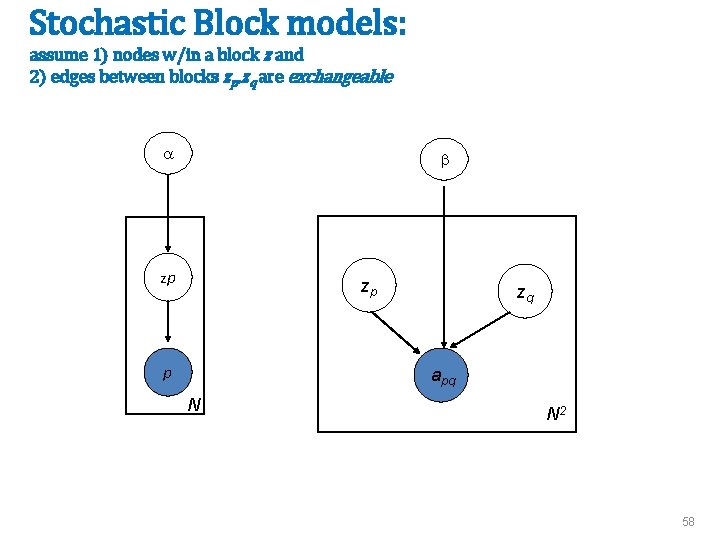
More terms • “Stochastic block model”, aka “Block-stochastic matrix”: – Draw ni nodes in block i – With probability pij, connect pairs (u, v) where u is in block i, v is in block j – Special, simple case: pii=qi, and pij=s for all i≠j • Question: can you fit this model to a graph? – find each pij and latent node block mapping 55

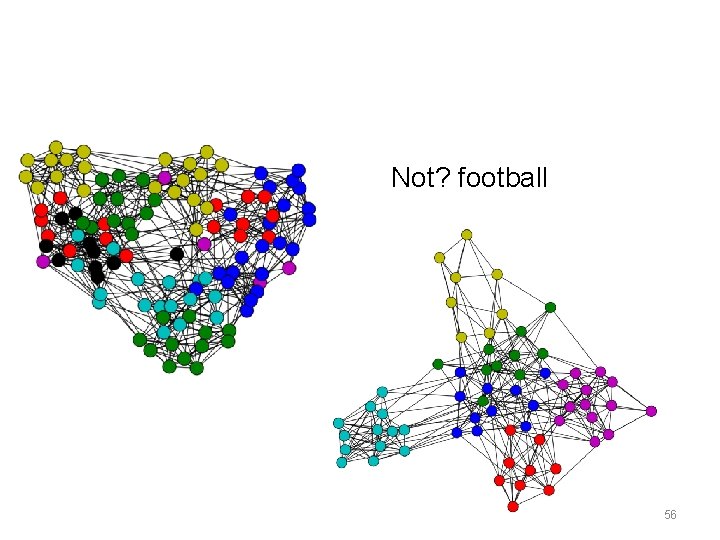
Not? football 56

Not? books 57

Stochastic Block models: assume 1) nodes w/in a block z and 2) edges between blocks zp, zq are exchangeable a b zp zp p zq apq N N 2 58

Another mixed membership block model 59

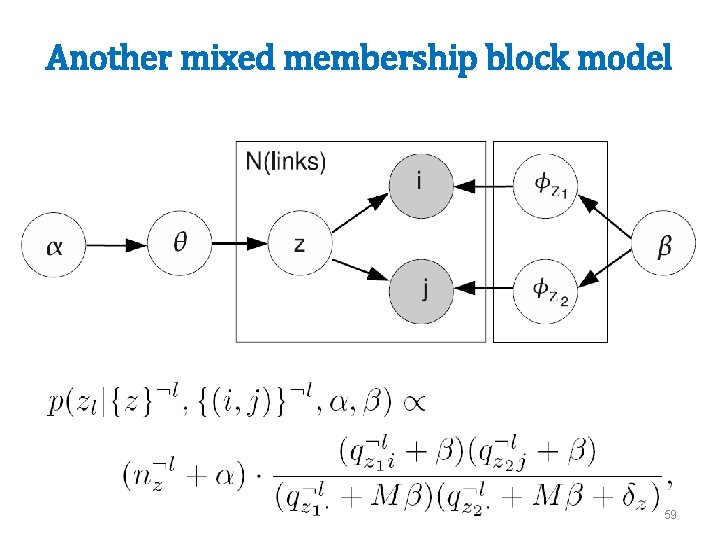
Another mixed membership block model z=(zi, zj) is a pair of block ids nz = #pairs z qz 1, i = #links to i from block z 1 qz 1, . = #outlinks in block z 1 δ = indicator for diagonal M = #nodes 60

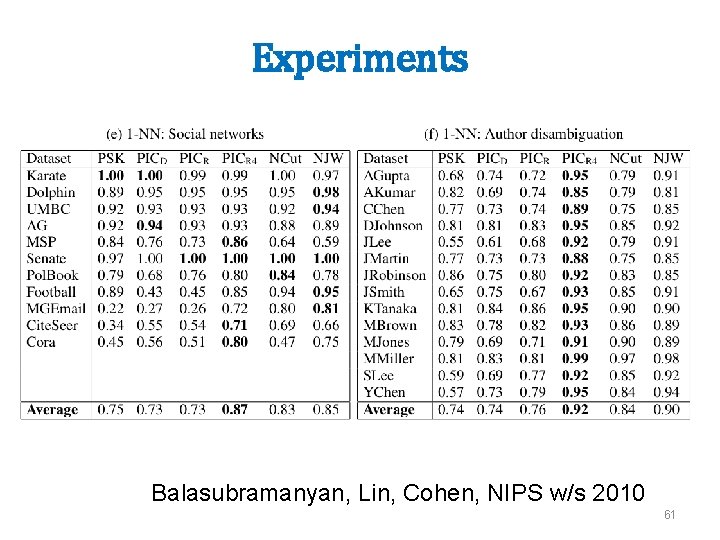
Experiments Balasubramanyan, Lin, Cohen, NIPS w/s 2010 61