Speech Processing Acoustics of Speech Production Physics of


























































































- Slides: 124

Speech Processing Acoustics of Speech Production

Physics of Sound u Sound Generation: n Vibration of particles in a medium (e. g. , air, water). u Speech Production: n Perturbation of air particles near the lips. u Speech Communication: n Propagation of particle vibrations/perturbations as chain reaction through free space (e. g. , a medium like air) from the source (i. e. , lips of a speaker) to the destination (i. e. , ear of a listener). n Listener’s ear-drum caused vibrations trigger series of transductions initiated by this mechanical motion leading to neural firing ultimately perceived by the brain. 12/1/2020 Veton Këpuska 2

Physics of Sound u A sound wave is the propagation of a disturbance of particles through an air medium (or more generally any conducting medium) without the permanent displacement of the particles themselves. u Alternating compression and rarefaction phases create a traveling wave. u Associated with disturbance are local changes in particle: n Pressure n Displacement n Velocity 12/1/2020 Veton Këpuska 3

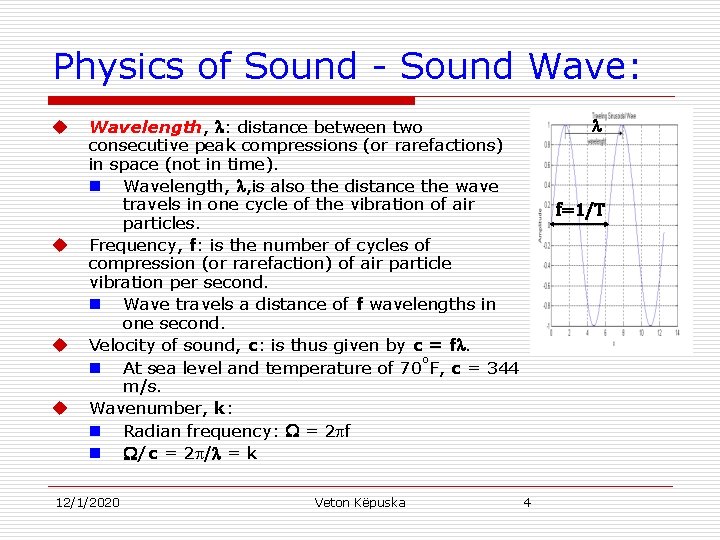
Physics of Sound - Sound Wave: u u Wavelength, : distance between two consecutive peak compressions (or rarefactions) in space (not in time). n Wavelength, , is also the distance the wave travels in one cycle of the vibration of air particles. Frequency, f: is the number of cycles of compression (or rarefaction) of air particle vibration per second. n Wave travels a distance of f wavelengths in one second. Velocity of sound, c: is thus given by c = f. o n At sea level and temperature of 70 F, c = 344 m/s. Wavenumber, k: n Radian frequency: = 2 f n /c = 2 / = k 12/1/2020 Veton Këpuska 4 f=1/T

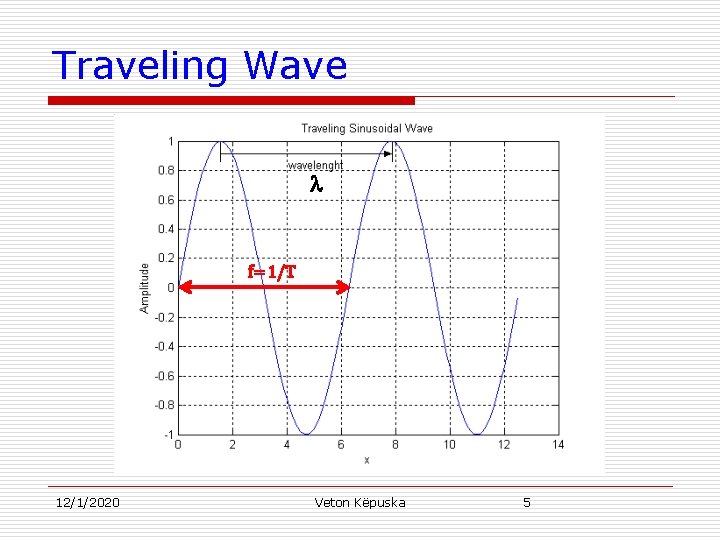
Traveling Wave f=1/T 12/1/2020 Veton Këpuska 5

Physics of Sound u Example 4. 1 n Suppose the frequency of a sound wave is f = 50 Hz, 1000 Hz, and 10000 Hz. Also assume that the velocity of sound at sea level is c = 344 m/s. n The wavelength of sound wave is respectively: = 6. 88 m, 0. 344 m and 0. 0344 m. n Speech sounds have wide range of wavelengths values: n Audio range: u fmin = 30 Hz ⇒ =11. 5 m u fmax = 20 k. Hz ⇒ =0. 0172 m 12/1/2020 Veton Këpuska 6

Physics of Sound: adiabatic process u In audible range, propagation of sound wave is considered to be an adiabatic process, that is, n 12/1/2020 heat generated by particle collision during pressure fluctuations, has no time to dissipate away and therefore temperature changes occur locally in the medium. Veton Këpuska 7

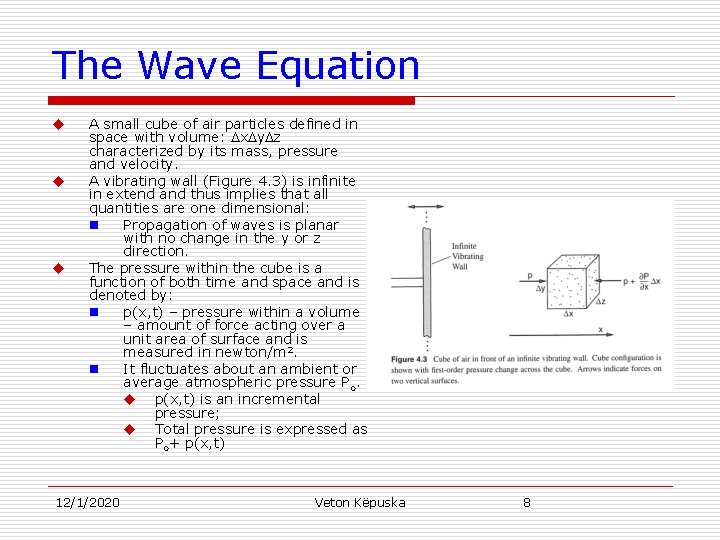
The Wave Equation u u u A small cube of air particles defined in space with volume: x y z characterized by its mass, pressure and velocity. A vibrating wall (Figure 4. 3) is infinite in extend and thus implies that all quantities are one dimensional: n Propagation of waves is planar with no change in the y or z direction. The pressure within the cube is a function of both time and space and is denoted by: n p(x, t) – pressure within a volume – amount of force acting over a unit area of surface and is measured in newton/m 2. n It fluctuates about an ambient or average atmospheric pressure Po. u p(x, t) is an incremental pressure; u Total pressure is expressed as Po+ p(x, t) 12/1/2020 Veton Këpuska 8

The Wave Equation u Atmospheric pressure is typically Po= 105 newtons/m 2. u Threshold of hearing (minimal perceivable pressure above atmospheric pressure) is about p(x, t)=2 x 10 -5 newtons/m 2 at 1000 Hz. u Threshold of hearing pain is about 20 newtons/m 2 - p(x, t). n Human ear is extremely sensitive to pressure changes and covers a large dynamic range. 12/1/2020 Veton Këpuska 9

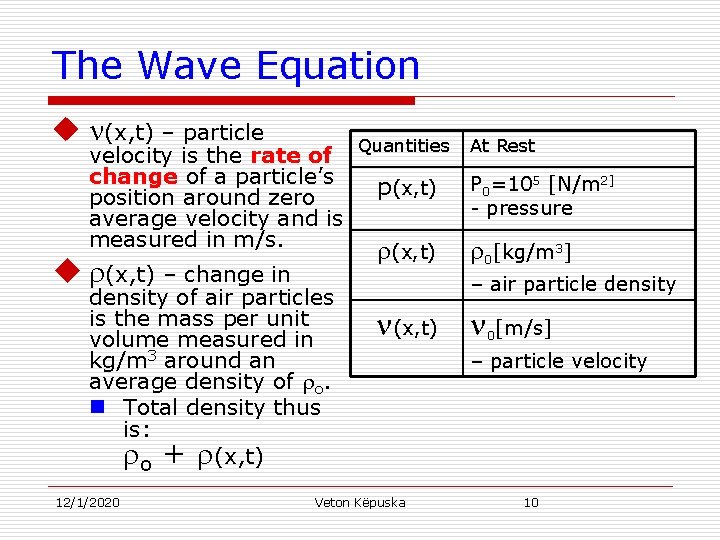
The Wave Equation u (x, t) – particle velocity is the rate of Quantities At Rest change of a particle’s P 0=105 [N/m 2] p (x, t) position around zero - pressure average velocity and is measured in m/s. 3 u (x, t) – change in density of air particles is the mass per unit volume measured in kg/m 3 around an average density of o. n Total density thus is: o + (x, t) 12/1/2020 (x, t) 0[kg/m (x, t) 0[m/s] Veton Këpuska ] – air particle density – particle velocity 10

The Wave Equation u Three laws of physics are used to derive wave equations: 1. Newton’s Second Law of Motion: u Total force exerted on a volume of space is equal to the mass of that volume times its acceleration. 12/1/2020 Veton Këpuska 11

The Wave Equation 2. Gas Law of Thermodynamics: u Relates pressure, volume and temperature. u Under adiabatic conditions, of interest for speech sound propagation, reduces to the relation: u u P – total pressure on the cube V – volume of the cube C – constant. = 1. 4 – is the ratio of specific heat of air at constant pressure to the specific heat of air at constant volume. http: //scienceworld. wolfram. com/physics/. More specifically: u 12/1/2020 The definition of an adiabatic process is one for which no heat is gained or lost. In current situation it means that there is no heat transferred. Veton Këpuska 12

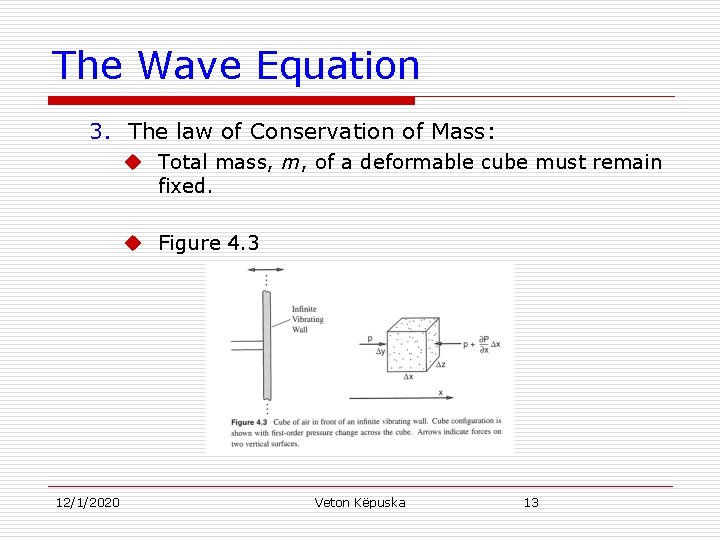
The Wave Equation 3. The law of Conservation of Mass: u Total mass, m, of a deformable cube must remain fixed. u Figure 4. 3 12/1/2020 Veton Këpuska 13

The Wave Equation u Assumptions: 1. 2. There is negligible friction of air particles in the cube with those outside the cube. That is, there is no shearing pressure due to horizontal movement of the air. Shearing pressure is referred to as viscosity. n The pressure on the cube is due to only forces on the two vertical faces of the cube as illustrated in Figure 4. 3 Cube of air is small enough so that the pressure change across the cube in the horizontal dimension ( x) is of the “first order”, corresponding to sounds of not extremely large intensity. n This means that the second and higher order terms in Taylor series expansion of the pressure function with respect to the x argument can be neglected: 3. 12/1/2020 Density of air particles is constant in the cube and equal to the average atmospheric density. Veton Këpuska 14

The Wave Equation u Pressure and (net) force: p u From the constant density of the cube assumption: u Acceleration of a volume of air is denoted by: 12/1/2020 Veton Këpuska 15

The Wave Equation u From Newton’s Second Law of Motion: u Net force acting on the cube of air: u After canceling terms we have: 12/1/2020 Veton Këpuska 16

The Wave Equation u Note on replacement of d /dt (total derivative) with ∂ /∂t (partial derivative). n Because (x, t) is a function of space as well as time, the true acceleration of the air particles is given by: n Nonlinear equation in the variable because the particle velocity multiplies ∂ /∂x. u Difficult to determine general solution. 12/1/2020 Veton Këpuska 17

Note on Partial Derivatives 12/1/2020 Veton Këpuska 18

The Wave Equation u Original equation is the approximation of the above and is accurate for conditions were the correction term ∂ /∂x is significantly lower relative to d /dt. u This approximation, in vector form, rules out rotational or jet flow and thus the possibility of modeling vortices along the oral cavity (as alluded to in Chapter 3 of the text book) u Completion of derivation of the wave equation requires the use of Gas Law and Conservation of Mass principle which can be shown to result in the relation [L. L. Beranek, Acoustics, Mc. Graw-Hill, New York, NY, 1954]: 12/1/2020 Veton Këpuska 19

The Wave Equation u First form of Wave Equation: u Second form is obtained by differentiating equations above with respect to x and t respectively: 12/1/2020 Veton Këpuska 20

The Wave Equation u The last pair of equations can be combined to form the second-order partial differential equation in pressure only: u Likewise, the above pair of equations can be combined to form the second-order partial differential equation in velocity only: 12/1/2020 Veton Këpuska 21

The Wave Equation u Alternate forms of Wave Equations are given in equations (4. 5) and (4. 6). u They are approximately valid under the following assumptions: 1. The medium is homogeneous (constant density), 2. The pressure change across a small distance can be linearized, 3. There is no viscosity of air particles, 4. The particle velocity is small (implying that the full derivative of the velocity term is not necessary), and 5. Sound propagation is adiabatic process. 12/1/2020 Veton Këpuska 22

Uniform Tube Model Veton Këpuska

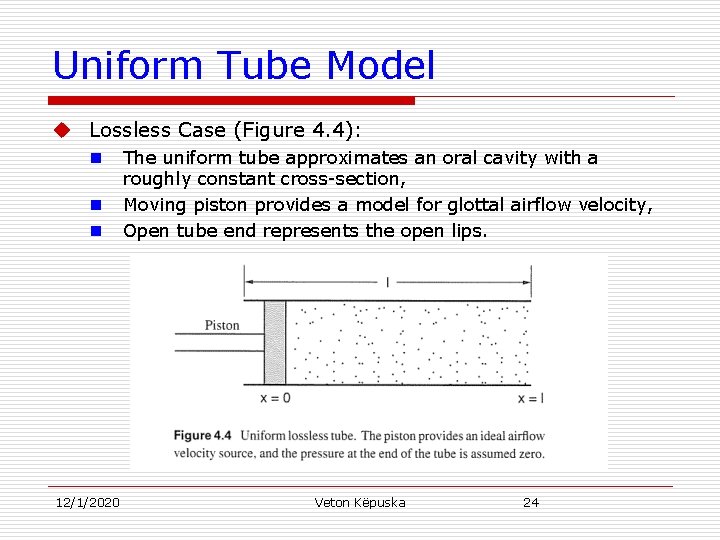
Uniform Tube Model u Lossless Case (Figure 4. 4): n n n 12/1/2020 The uniform tube approximates an oral cavity with a roughly constant cross-section, Moving piston provides a model for glottal airflow velocity, Open tube end represents the open lips. Veton Këpuska 24

Uniform Tube Model u By definition this tube has a time- and space-invariant cross-section A(x, t) = A. u Planar sound waves are assumed to propagate longitudinally along the x-axis. u Assuming for the moment that there is no friction along the walls of the tube. u The tube is open on one side at x=l; l-thus specifies the length of the uniform tube. 12/1/2020 Veton Këpuska 25

Uniform Tube Model u Air pressure at the lips is assumed to be equal to atmospheric pressure and thus p(x=l, t)=0. u At the lips however, there are variations of particle velocities. u Analogy to electrical short-circuit: n Piston (particle velocity source) is analogous to an ideal current source: u Piston moves independently of pressure n Pressure variation is analogous to a voltage differential. 12/1/2020 Veton Këpuska 26

Uniform Tube Model u Case of one-dimensional (planar) sound propagation: n Use the volume velocity of air vs. particle velocity. n Volume velocity, denoted as u(x, t), is defined as the rate of flow of air particles perpendicularly through a specified area. n Express volume velocity of uniform tube in terms of particle velocity: u u(x, t) = A (x, t) 12/1/2020 Veton Këpuska 27

Uniform Tube Model u Rewrite Wave Equations (4. 1) and (4. 4) in terms of volume velocity: u It can be shown (see Exercise 4. 1) that two solutions of the following form satisfy Equation (4. 7): 12/1/2020 Veton Këpuska 28

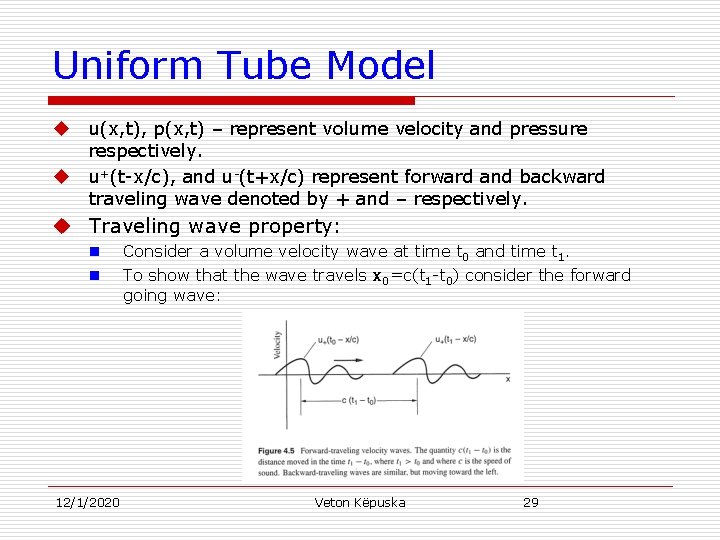
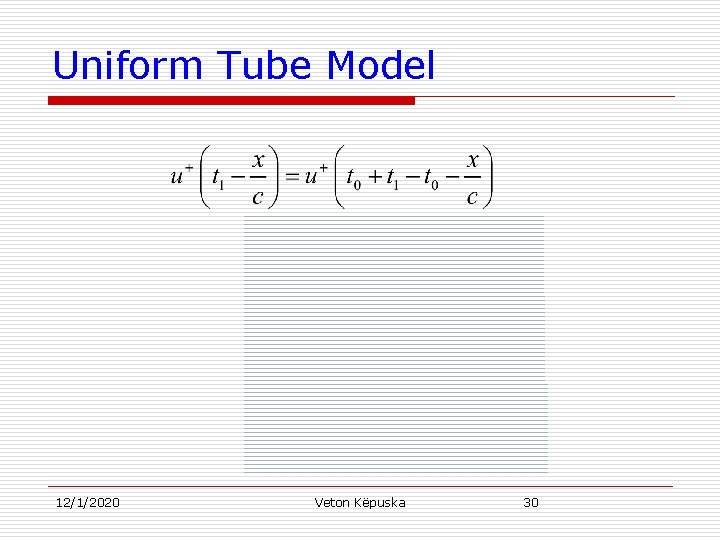
Uniform Tube Model u u u(x, t), p(x, t) – represent volume velocity and pressure respectively. u+(t-x/c), and u-(t+x/c) represent forward and backward traveling wave denoted by + and – respectively. u Traveling wave property: n n 12/1/2020 Consider a volume velocity wave at time t 0 and time t 1. To show that the wave travels x 0=c(t 1 -t 0) consider the forward going wave: Veton Këpuska 29

Uniform Tube Model x 0 12/1/2020 Veton Këpuska 30

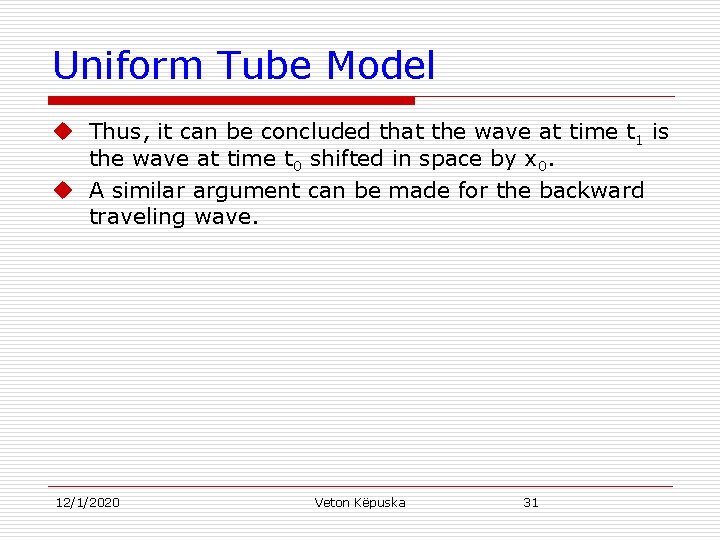
Uniform Tube Model u Thus, it can be concluded that the wave at time t 1 is the wave at time t 0 shifted in space by x 0. u A similar argument can be made for the backward traveling wave. 12/1/2020 Veton Këpuska 31

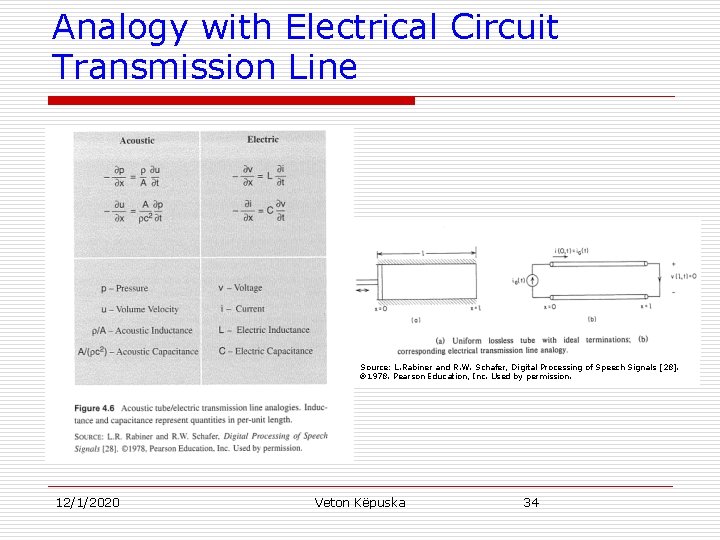
Uniform Tube Model u Electrical Circuit Analogy: n Plane-wave sound propagation is similar to that for plane-wave propagation along an electrical transmission line: u Voltage Pressure u Current Volume velocity. 12/1/2020 Veton Këpuska 32

Uniform Tube Model n /A - acoustic inductance n A/ c 2 - acoustic capacitance n These quantities reflect u “inertia” (mass or density) and u “springiness” (elasticity) of the air medium, respectively. u See Figure 4. 6 for details. 12/1/2020 Veton Këpuska 33

Analogy with Electrical Circuit Transmission Line Source: L. Rabiner and R. W. Schafer, Digital Processing of Speech Signals [28]. 1978. Pearson Education, Inc. Used by permission. 12/1/2020 Veton Këpuska 34

Uniform Tube Model n Steady state solution written in the frequency domain using a complex sinewave representation: u i(x, t)=I(x, )ej (t-x/c) – sinusoidal current wave of frequency traveling forward at speed c in the transmission line medium. n General form of the solution for a uniform-tube configuration was given previously. n Specific solution is determined based on (idealized) boundary conditions: u x=0 – volume velocity: u(0, t)=U( )ej t, or u(0, t)=ug(t)=Ug( )ej t u x=l – pressure at the lips: p(l, t)=0 12/1/2020 Veton Këpuska 35

Uniform Tube Model u Because volume velocity driving function is sinusoidal, we assume: 12/1/2020 Veton Këpuska 36

Uniform Tube Model u Determine constants k+ and k- based on boundary conditions: n Boundary condition at the source gives: n The boundary condition at the open-end gives: 12/1/2020 Veton Këpuska 37

Uniform Tube Model u Solving the system of equations yields: 12/1/2020 Veton Këpuska 38

Uniform Tube Model u Substituting obtained solution into the Equation pair we get: 12/1/2020 Veton Këpuska 39

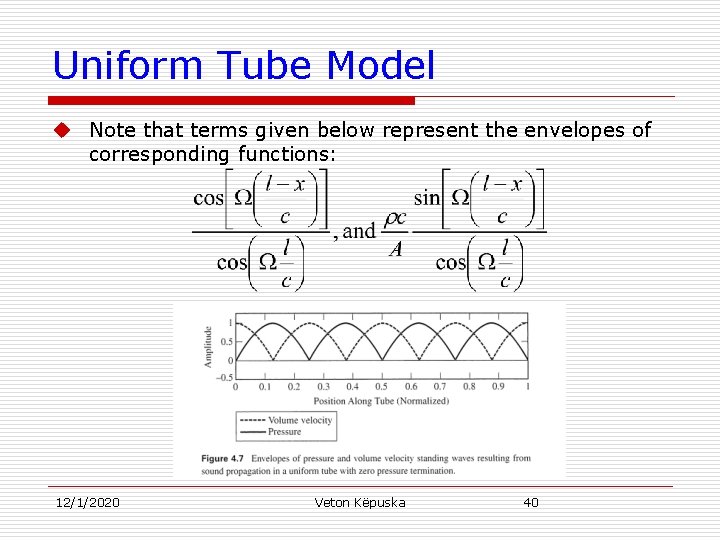
Uniform Tube Model u Note that terms given below represent the envelopes of corresponding functions: 12/1/2020 Veton Këpuska 40

Uniform Tube Model u Note: n 90 o out of phase of pressure and velocity. Thus pressure and velocity are orthogonal in space. n The two functions are also orthogonal in time (j multiplier of the pressure function). n Orthogonality of functions in space and time implies that acoustic potential and kinetic energies along the tube are also orthogonal. 12/1/2020 Veton Këpuska 41

Uniform Tube Model u Volume velocity at the lips: u Define complex amplitude at the open tube end for complex input Ug( )ej t: 12/1/2020 Veton Këpuska 42

Uniform Tube Model u Relate volume velocity frequency response at the open end of the tube to volume velocity at the glottis (frequency response of the Uniform Tube): 12/1/2020 Veton Këpuska 43

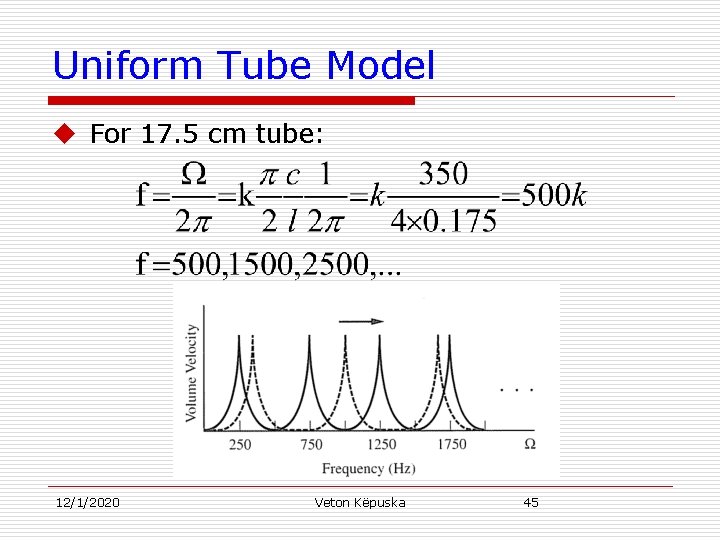
Uniform Tube Model u Example 4. 2 n Consider a uniform tube of length l=35 cm. If speed of sound is 350 m/s calculate its resonances in Hz. Compare its resonances with a tube of length l = 17. 5 cm. n f= /2 ⇒ 12/1/2020 Veton Këpuska 44

Uniform Tube Model u For 17. 5 cm tube: 12/1/2020 Veton Këpuska 45

Uniform Tube Model u A quantity that relates pressure and volume velocity is referred to as acoustic impedance (analogous to electric impedance): u For a very short tube with length denoted by x, using Taylor series expansion of the tangent function (at the tube’s end), an approximation for acoustic impedance is obtained: 12/1/2020 Veton Këpuska 46

Uniform Tube Model u Transfer Function: n Can be obtained by noting the relationship: u s= +j ⇒ n Thus: 12/1/2020 Veton Këpuska 47

Uniform Tube Model u Previous equation can be written as (Flanagan): 12/1/2020 Veton Këpuska 48

Effect of Energy Loss u Recall the lossless tube wave equations: u Energy loss can be described by differential equations coupled to the wave equations above. u Coupled equations are typically: n Complicated and n Closed-form solution is difficult to obtain. u Solution is often found by numerical simulation. 12/1/2020 Veton Këpuska 49

Effect of Energy Loss u Losses due to Wall Vibration n To predict the effect of wall vibration on sound propagation, partial differential equations of lossless tube repeated in previous slide, are generalized to a non-uniform time-varying tube. n Under certain assumptions: Cross-section of a non-uniform tube does not change “to rapidly”: u in space (e. g. , x-direction), as well as u in time. n It has been shown (Portnoff) that sound propagation in a non-unfirm tube with time- and space-varying cross-section A(x, t) is given by: 12/1/2020 Veton Këpuska 50

Losses due to Wall Vibration u Model of non-uniform tube with cross section A(x, t) is given by: 12/1/2020 Veton Këpuska 51

Losses due to Wall Vibration u Portnoff then assumed that small, differential pieces of the surface of the wall (d ), are independent. u Mechanics of each piece modeled by: n Mass – mw n Spring constant – kw n Damping constant - bw per unit surface area as illustrated in Figure 4. 9 presented in the next slide u Because change in cross section relative to average cross-section is small: n A(x, t) = Ao(x, t) + A(x, t) n Where: u A(x, t) – linear perturbation about the u Ao(x, t) – average area. 12/1/2020 Veton Këpuska 52

Losses due to Wall Vibration 12/1/2020 Veton Këpuska 53

Losses due to Wall Vibration u Using the lumped parameter model presented in previous slide the second order differential equation for the perturbation term is given by: Mass per unit surface area Dumping per unit surface area Spring constant per unit surface area u Resulting frequency response of the numerical simulation model is shown in Figure 4. 10 a) in the next slide. 12/1/2020 Veton Këpuska 54

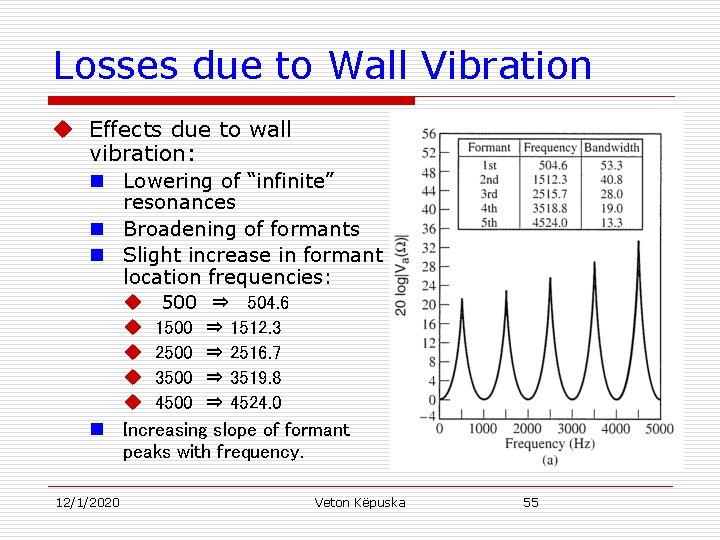
Losses due to Wall Vibration u Effects due to wall vibration: n Lowering of “infinite” resonances n Broadening of formants n Slight increase in formant location frequencies: u 500 ⇒ 504. 6 u 1500 ⇒ 1512. 3 u 2500 ⇒ 2516. 7 u 3500 ⇒ 3519. 8 u 4500 ⇒ 4524. 0 n Increasing slope of formant peaks with frequency. 12/1/2020 Veton Këpuska 55

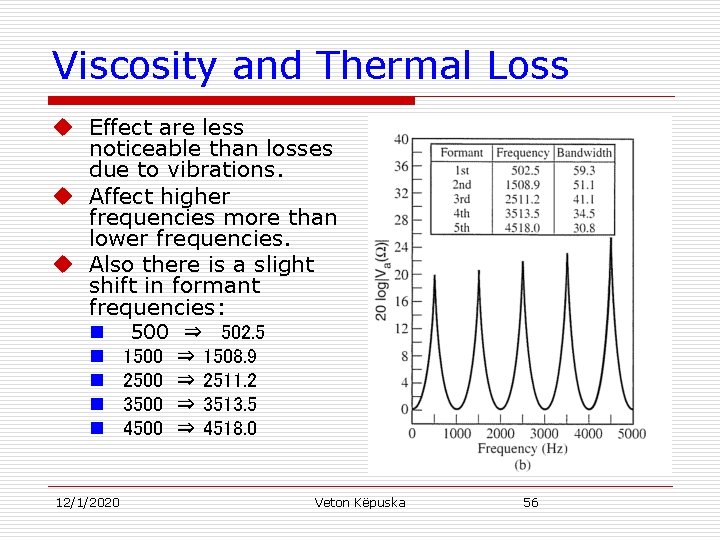
Viscosity and Thermal Loss u Effect are less noticeable than losses due to vibrations. u Affect higher frequencies more than lower frequencies. u Also there is a slight shift in formant frequencies: n n n 12/1/2020 500 ⇒ 502. 5 1500 ⇒ 1508. 9 2500 ⇒ 2511. 2 3500 ⇒ 3513. 5 4500 ⇒ 4518. 0 Veton Këpuska 56

Boundary Effects u Up to now assumed: n Pressure at the lips is zero, and n Volume velocity source is ideal, ⇒ There is no energy loss at the output or input of uniform tube. u A more realistic assumptions is depicted in Figure 4. 11: n Glottal load n Radiation at the lips 12/1/2020 Veton Këpuska 57

Boundary Effects u Radiation loss at the lips u Glottal source effects 12/1/2020 Veton Këpuska 58

Radiation Impedance u The effect of radiation at the lips can be simplified by determining the acoustic impedance “seen” by the vocal tract toward the outside “world”. u Acoustic impedance can be approximated by determining the impedance felt by a piston in a rigid sphere representing the head. This assumption leads to an expression that can not be written in closed form (Morse Ingard). n In the second form approximation the piston is assumed small compared to the sphere diameter, modeling a piston set in an infinitely large wall (see Figure 4. 11 in previous slide) 12/1/2020 Veton Këpuska 59

Radiation Impedance u For the latest configuration: n Acoustic Impedance Radiation resistance || Radiation Inductance Energy loss via sound propagation from lips Inertial air mass pushed out at lips n For the infinite wall, Flanagan has given values of: 12/1/2020 Veton Këpuska 60

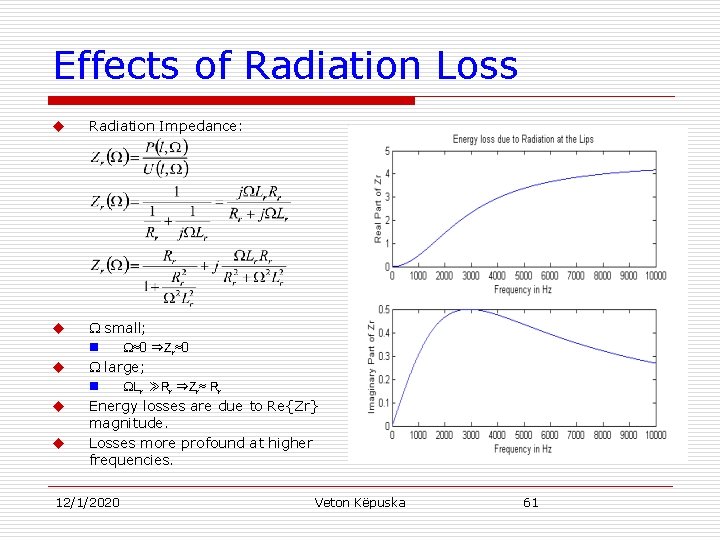
Effects of Radiation Loss u Radiation Impedance: u small; n ≈0 ⇒Zr≈0 large; n Lr ≫Rr ⇒Zr≈ Rr Energy losses are due to Re{Zr} magnitude. Losses more profound at higher frequencies. u u u 12/1/2020 Veton Këpuska 61

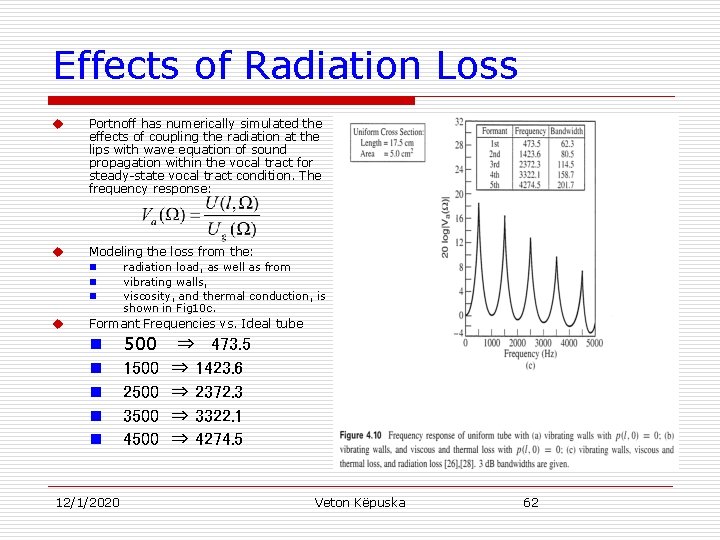
Effects of Radiation Loss u Portnoff has numerically simulated the effects of coupling the radiation at the lips with wave equation of sound propagation within the vocal tract for steady-state vocal tract condition. The frequency response: u Modeling the loss from the: n radiation load, as well as from n vibrating walls, n viscosity, and thermal conduction, is u Formant Frequencies vs. Ideal tube shown in Fig 10 c. n n n 12/1/2020 500 ⇒ 473. 5 1500 ⇒ 1423. 6 2500 ⇒ 2372. 3 3500 ⇒ 3322. 1 4500 ⇒ 4274. 5 Veton Këpuska 62

Glottal Source Effects u u u Most difficult addendum to simple uniform tube model because the glottal volume velocity has been shown to be nonlinearly related to the pressure variations in the vocal tract. The simplification of the nonlinear, time-varying two-mass vocal fold model involved linearization (Flanagan and Ishizaka) of model as a time-invariant glottal impedance consisting of a resistance Rg in series with an inductance Lg: Note: n small; u ≈0 n large; u Lg≫ 12/1/2020 ⇒Zg( )≈ Rg ; Resistive ⇒Zg( )≈ j Lg ; Inductive Veton Këpuska 63

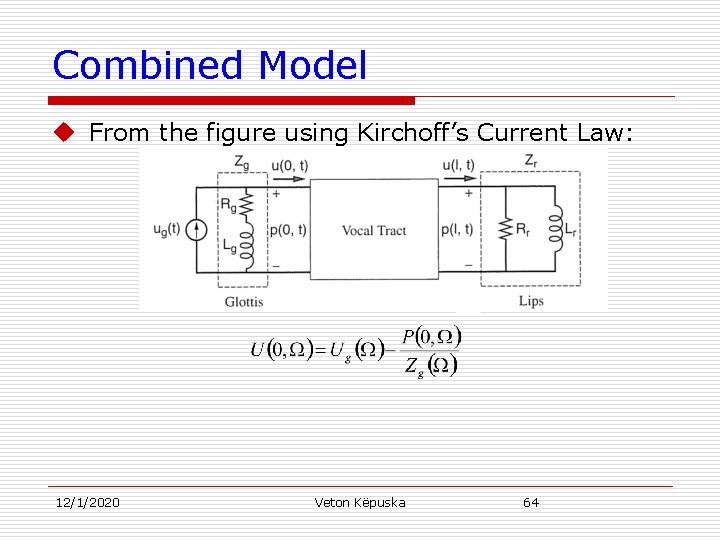
Combined Model u From the figure using Kirchoff’s Current Law: 12/1/2020 Veton Këpuska 64

Combined Model u u u Up to now we have found the frequency response relating volume velocity at the lips, U(l, ), to input volume velocity at the glottis, Ug(l, ). In practice we measure the pressure at the lips (not volume velocity) with a pressure sensitive transducer (e. g. , microphone). The pressure-to-volume velocity frequency response can be found as: 12/1/2020 Veton Këpuska 65

A Complete Model u So far assumed a uniform acoustic tube with time invariant: n n Cross-section, and Glottal model. n This approach leads to a discrete-time model whose implementation can be made computationally efficient using digital signal processing techniques. u Those assumptions are unrealistic. u For realistic modeling complex nonlinear differential equations need to be solved. u Numeric solutions applied only to uniform tube modeling. Non-uniform time varying cross-section modeling are cumbersome. u A simpler alternative is to estimate the desired transfer function Va(s) through a concatenated tube approximation of the cross-section function A(x, t). 12/1/2020 Veton Këpuska 66

Summary of Effects of Losses 1. 2. 3. Slight increase in resonance locations due to various sources of energy loss. Bandwidths of lower resonances are primarily affected by vibrating walls, and to lesser degree by glottal effects. Bandwidths of higher resonances are affected by viscous, thermal and radiation losses. 12/1/2020 Veton Këpuska 67

A Discrete-Time Model Based on Tube Concatenation u An effective and practical approach to vocal tract modeling is to assume that the vocal tract is comprised of concatenation of a number of uniform lossless tubes. u Losses in this model are caused by the discontinuities at the boundaries between tubes. 12/1/2020 Veton Këpuska 68

A Discrete-Time Model Based on Tube Concatenation u Frequency response of vocal tract, Va( )=U(l, )/Ug( ), is easy to obtain due to linearity of the model. n n n Radiation impedance can be modified to match observed formant bandwidths. Concatenated tube model leads to resulting all-pole model which in turn leads to linear prediction speech analysis. Draw back of this technique is that although frequency response predicted from concatenated tube model can be made to approximately match spectral measurements, the concatenated tube model is less accurate in representing the physics of sound propagation than the coupled partial differential equation models. u The contributions of energy loss from: n Vibrating walls n Viscosity, n Thermal conduction, as well as n Nonlinear coupling between the glottal and vocal tract airflow, Are not represented in the lossless concatenated tube model. 12/1/2020 Veton Këpuska 69

Sound Propagation in the Concatenated Tube Model u Consider an N-tube model of figure 4. 14. Each tube has length lk and cross sectional area of Ak. u Assume: n n No losses Planar wave propagation u Recall equation 4. 8, that we rewrite for section k: 0≤x≤l k 12/1/2020 Veton Këpuska 70

Sound Propagation in the Concatenated Tube Model u u Boundary conditions: Physical principle of continuity: n u Pressure and volume velocity must be continuous both in time and in space everywhere in the system: At k’th/(k+1)’st junction we have: 12/1/2020 Veton Këpuska 71

Sound Propagation in the Concatenated Tube Model u Applying boundary conditions: 12/1/2020 Veton Këpuska 72

Sound Propagation in the Concatenated Tube Model u u Last equations in previous slide illustrate the general rule that at a discontinuity along x in the area function A(x, t) there occur propagation and reflection of the traveling wave: n In each tube part of the a traveling wave propagates to the next tube and part is reflected back (Figure 4. 15). Leads to definition of Reflection Coefficient. 12/1/2020 Veton Këpuska 73

Sound Propagation in the Concatenated Tube Model u Since Ak>0, it follows that -1≤r≤ 1. u Substituting r in last two equations the following is obtained: 12/1/2020 Veton Këpuska 74

Boundary conditions at lips u For N-tubes the boundary conditions at the lips relate pressure p. N(l. N, t) and the volume velocity u. N(l. N, t) at the output of Nth tube. u Recall: 12/1/2020 Veton Këpuska 75

Sound Propagation in the Concatenated Tube Model u In the signal flow graph representation: u Typically Zr is unknown or hard to obtain. However, radiation at the lips can be also modeled with an additional tube of cross-section AN+1 and infinite length. u AN+1 can be selected such that Zr = c/AN+1. Thus r. L becomes: 12/1/2020 Veton Këpuska 76

Sound Propagation in the Concatenated Tube Model u Then: 12/1/2020 Veton Këpuska 77

Boundary conditions at Glottis u Recall Figure 4. 11 but now make Zg a purely resistive load. Then using Kirchoff’s current law the following is obtained: u Then from earlier expressions for volume velocity and pressure within a uniform tube (Equation 2. 7) we have: u Solving for the forward-going traveling wave we get: 12/1/2020 Veton Këpuska 78

Boundary conditions at Glottis u Similarly to the approach taken for modeling radiation at the lips: n n n 12/1/2020 If Zg( ) is complex (as with complex Zr( )) a differential equation realization of the glottal boundary condition is required. The glottal impedance can be models with an additional tube of cross-section A 0 and infinite in length similarly to the radiation impedance at the lips. If we make A 0 such that Zg= c/A 0, then expression for rg becomes: Veton Këpuska 79

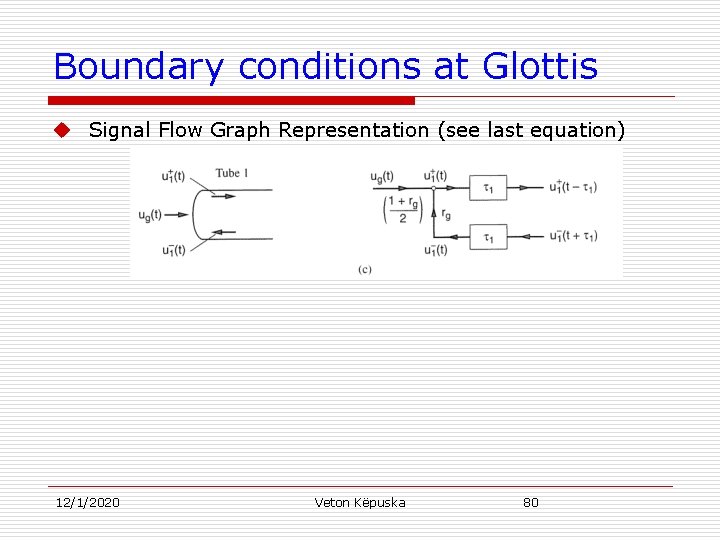
Boundary conditions at Glottis u Signal Flow Graph Representation (see last equation) 12/1/2020 Veton Këpuska 80

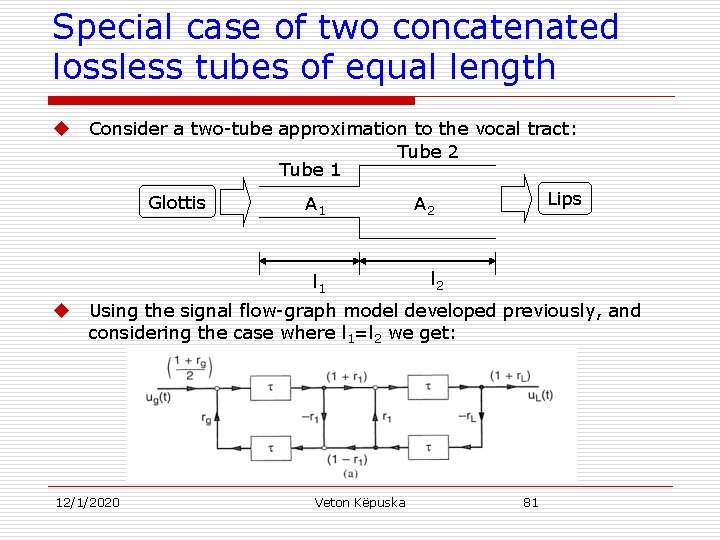
Special case of two concatenated lossless tubes of equal length u Consider a two-tube approximation to the vocal tract: Tube 2 Tube 1 Glottis A 1 l 1 u Lips A 2 l 2 Using the signal flow-graph model developed previously, and considering the case where l 1=l 2 we get: 12/1/2020 Veton Këpuska 81

Special case of two concatenated lossless tubes of equal length u Transfer function relating the volume velocity at the lips to the glottis is given by: 12/1/2020 Veton Këpuska 82

Discrete-Time Realization u Consider a model consisting of N lossless concatenated tubes of total length l. u Each individual tube is equal length: n Delay through each tube is equal: = x/c and x=l/N. u Let ug(t) = (t): n If there is no reflection in the intermittent tubes the output is then: va(t)= (t-N ). n With partial reflections the output is: u 2 is the round-trip delay within the tube. u Earliest arrival occurs at N and successive occurrences at multiples of 2 due to multiple reflections and propagations. 12/1/2020 Veton Këpuska 83

Discrete-Time Realization b 0 va(t) b 1 0 b 2 … N N +4 N +2 bk t N +k 2 u Because we are in continuous time representation, the Laplace transform of a delayed impulse response (t-t 0) is given by e-st 0: u The term e-s. N corresponds to the delay required to propagate through N sections. n n 12/1/2020 Because this delayed signal can be recovered with a simple time shift we will ignore the time delay of N. Making the change of variables s=j : we get the frequency response: Veton Këpuska 84

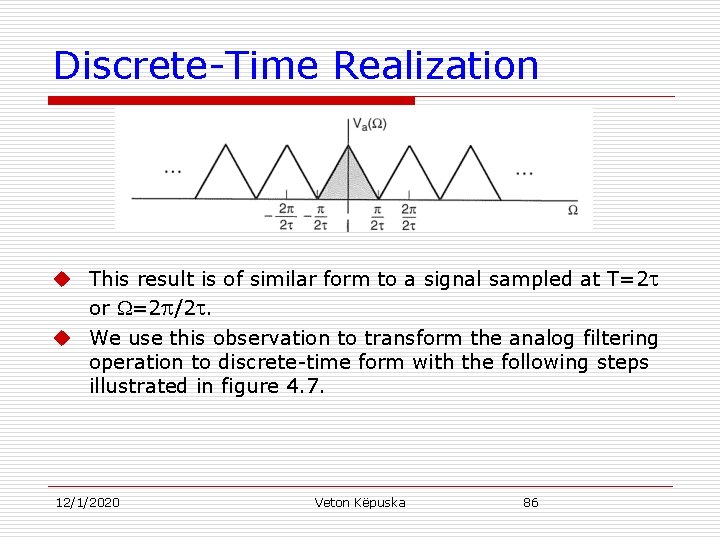
Discrete-Time Realization u This expression can be shown to be periodic with period 2 /2 : u Rationale: n By “discretization” of the continuous-space tube with space-interval x=l/N, and the corresponding timeinterval = x/c the periodicity is expected to appear in the transfer function representation. 12/1/2020 Veton Këpuska 85

Discrete-Time Realization u This result is of similar form to a signal sampled at T=2 or =2 /2. u We use this observation to transform the analog filtering operation to discrete-time form with the following steps illustrated in figure 4. 7. 12/1/2020 Veton Këpuska 86

Discrete-Time Realization 1. Using the impulse-invariance method, i. e. , replacing es. T with T=2 , the system function Va( ) is transformed into discrete-time: which, after replacing z=e s 2 =es. T the following is obtained: The frequency response V( )=V(z)|z=ej will be designed to match formant frequencies over the interval [- , ] 2. The Nyquist criterion is met if ug(t) is bandlimited to = /2 and there is no aliasing if sampling is done at T=2. 3. Because of the use of impulse-invariance method to perform filter conversion from a continuous-time to discrete-time, the continuous-time flow-graph is converted to discrete-time flow graph in straight forward manner. 12/1/2020 Veton Këpuska 87

Discrete-Time Realization 3. 4. Since a half-sample delay is difficult to implement (requires interpolation), lower-branch delays of the flow-graph are moved to upper branch observing that delays are preserved in any closed branch with this change as illustrated in the next figure. The final step in conversion is to multiply the discrete time frequency responses of the excitation and the vocal tract impulse response to form the frequency response of the discrete -time speech output. 12/1/2020 Veton Këpuska 88

Discrete-Time Realization u Note: n Spatial discretization ⇒Temporal discretization n x=l/N ⇒ T=2 =2(l/N)/c; n If input stimulus ug(t) is not strictly bandlimited then aliasing may occur. If spatial discretization does not result (e. g. , does not support) in sampling that abides by the Nyquist criterion, then aliasing may occur. Thus, to minimize aliasing due to discretization of continuous linear, time-invariant vocal tract model va(t), need to spatially sample the vocal tract with sufficient number of tubes to reduce aliasing. n n 12/1/2020 Veton Këpuska 89

Discrete-Time Realization u u Example: Let the vocal tract length be l=17. 5 cm (typical male speaker) and c=350 m/s. How many tubes are required to adequately represent a concatenated tube model under such conditions? Repeat the calculation for a vocal tract length of l=14 cm (typical for female speaker) and l=10 cm (typical for a child). Recall: 1. 2. Cutoff bandwidth is u Consider telephone speech where sample rate is 8000 Hz and thus the bandwidth is B≈2 4000 rad/s. 12/1/2020 Veton Këpuska 90

Discrete-Time Realization u For telephony speech we get: 1. 2. 3. Male speaker (l=17. 5 cm) Female speaker (l=14 cm) Child speaker (l=10 cm) 12/1/2020 Veton Këpuska ⇒ N=8 tubes ⇒ N=6. 4 ⇒ 7 tubes ⇒ N=4. 57 ⇒ 5 tubes 91

Discrete-Time Realization u Objective: To derive a general expression for V(z) in terms of the reflection coefficients: u To obtain directly from flow-graph is cumbersome. u Flow-graph’s modular structure, however, provides the way to compute the transfer function: n This transfer function can be shown to be: u a stable u all-pole function u with bandwidths determined solely by the loss due to Zg( ) and Zr( ), that is V(z) is of the form: 12/1/2020 Veton Këpuska 92

Discrete-Time Realization u Where the poles correspond to the formants of the vocal tract. u Moreover, by setting rg=1 (i. e. , Zg( )=∞) so that no loss occurs at the glottis, a recursive process can be set up for computing D(z): 12/1/2020 Veton Këpuska 93

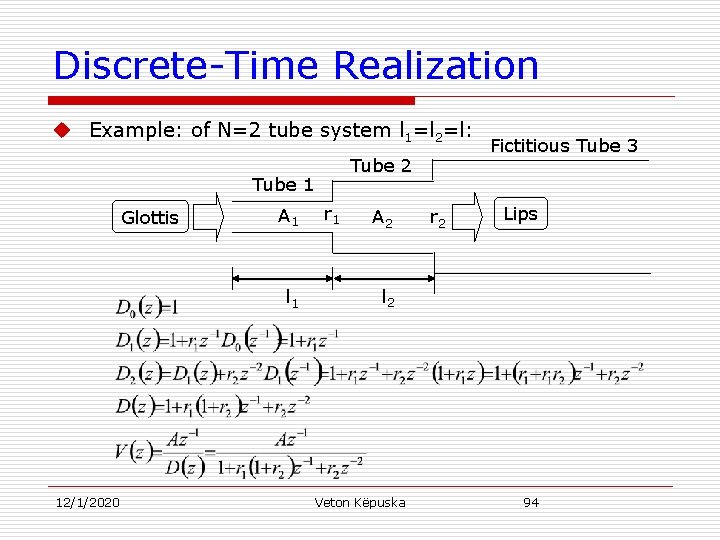
Discrete-Time Realization u Example: of N=2 tube system l 1=l 2=l: Tube 2 Tube 1 Glottis A 1 l 1 12/1/2020 r 1 A 2 r 2 Fictitious Tube 3 Lips l 2 Veton Këpuska 94

Discrete-Time Realization u Similarly to earlier approach, one can imagine the (N+1)’st tube is infinite in length with AN+1 selected so that r. N=r. L. n When Zg( )=∞ and Zr=0 ⇒ r. N=r. L=1 u Short circuit at the lips u No losses anywhere in the system ⇒zero bandwidth resonances arise. n With Zg( )=∞, Zr( ) – radiation impedance: u is the only source of loss in the system, and u it controls the resonance bandwidths. 12/1/2020 Veton Këpuska 95

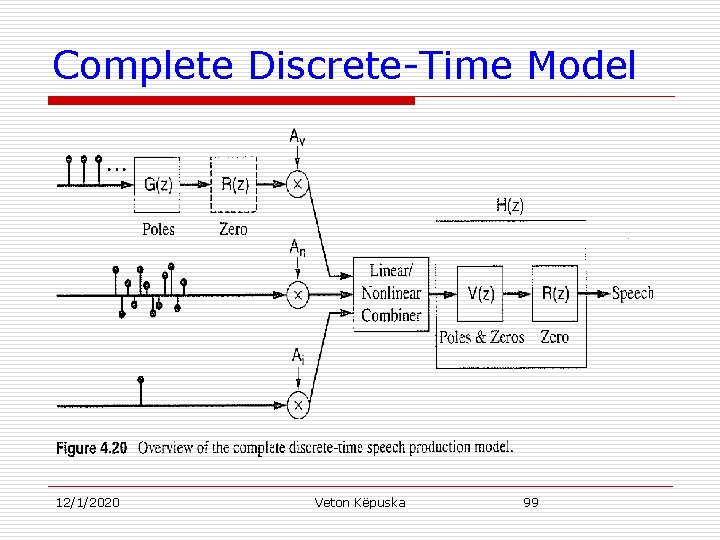
Complete Discrete-Time Model u In the previous section we have derived a discrete model of speech production that relates volume velocity at the lips with volume velocity at the glottis. u Acoustic sensors are pressure-sensitive transducers (e. g. , microphone, ear-drum, etc. ). Need to transform: n n Volume velocity to pressure, or Current into voltage u We have shown earlier (Equation 4. 26) the relationship from volume velocity to pressure at the lips that leads to: H(z)=V(z)R(z) Volume velocity transfer function 12/1/2020 Veton Këpuska Radiation Load 96

Complete Discrete-Time Model u V(z) – Discrete-time all-pole vocal tract model, and u R(z) – Discrete-time Radiation Impedance: n If approximated with a pure resistive load it can be shown (see Exercise 4. 20) that: 12/1/2020 Veton Këpuska 97

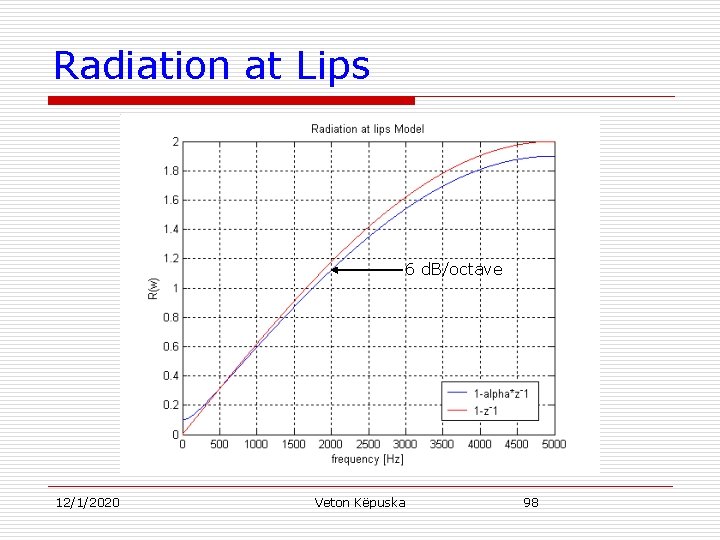
Radiation at Lips 6 d. B/octave 12/1/2020 Veton Këpuska 98

Complete Discrete-Time Model 12/1/2020 Veton Këpuska 99

Complete Discrete-Time Model 1. Voiced Source: u Recall: u This models assumes infinite glottal impedance (i. e. , no loss at the glottis) which in turn allowed us to model V(z) with an all-pole model: 12/1/2020 Veton Këpuska 100

Voiced Source: n V(z) and R(z) – minimum phase n G(z) – maximum phase – responsible for “gradual attack” (see Chapter 2 and notes). n If approximate differentiation of the radiation load is applied to the glottal input during voicing then additional network can be applied (i. e. , R(z) after G(z)). 12/1/2020 Veton Këpuska 101

Complete Discrete-Time Model 2. Unvoiced Source: u The input is not a periodic signal – rather a random sequence with typically flat spectrum (i. e. , white noise) as in fricative consonants: 3. Impulsive Source: u Occurs during plosive consonants, modeled by an impulse for simplicity: 12/1/2020 Veton Këpuska 102

Complete Discrete-Time Model u In noisy or impulsive source state, oral tract constrictions may give n Zeros (loss of energy by back-cavity antiresonance's), as well as n Poles u In these cases, the vocal tract transfer function V(z) has poles inside the unit circle, however, it may also have zeros inside and outside the unit circle as depicted in the transfer function expression given next: 12/1/2020 Veton Këpuska 103

Complete Discrete-Time Model u u Note that in real speech multiple sources can concurrently occur at the same time (e. g. , nasalized vowels, voiced fricatives, etc. ). They need to be combined to produce a more realistic sounds: n Linear combination is simple, however, not always adequate n Nonlinear combination difficult to determine. Presented model is referred to as “source/filter” performs well in matching measured spectrum or waveform or when only input/output relationships are required. An output measurement may not be uniquely invertible (i. e. , different vocal tract shapes, sources, nonlinear effects and subsystem coupling may yield similar output). An fascinating possible model refinement is presented in Section 4. 5 (Project topic). 12/1/2020 Veton Këpuska 104

History of Speech Synthesis From Dennis Klatt

Dennis Klatt's History of Speech Synthesis u http: //www. cs. indiana. edu/rhythmsp/ASA/Contents. html n u u u Audio clips of synthetic speech illustrating the history of the art and technology of synthetically produced human speech. The audio clips below are taken from Dennis Klatt's (1987), "Review of text-to-speech conversion for English" J. Acous. Soc. Amer. 82, 737 -793 (complete text available online thanks to David Maxey) with accompanying LP audio disk bound with the journal. We obtained permission from Dan Martin (former General Editor, JASA) to reproduce these audio clips on the web as a public service. See also the Smithsonian Speech Synthesis History Project by H. David Maxey for additional information on this topic. The ASA retains the copyright to these recordings. For further details about the synthesis methods, see Klatt's article. http: //www. mindspring. com/~ssshp/ssshp_cd/dk_737 b. h tm 12/1/2020 Veton Këpuska 106

12/1/2020 Veton Këpuska 107

Brief Chronological Development of Speech Synthesis (1922) u 1922 Stewart, J. Q. , “An Electrical Analogue of the Vocal Organs, ” Nature 110, pp. 311 -312 F 0 12/1/2020 System Buzzer Resonator Circuit 1 Resonator Circuit 2 Source Formant 1 Formant 2 Veton Këpuska Speech Out 108

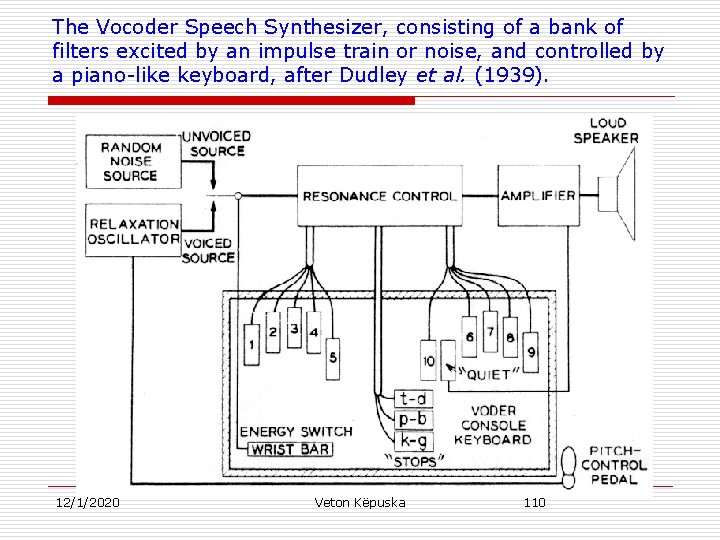
1939 The Vocoder u Dudley, H. “The Vocoder, ” Bell Labs, Rec 17, pp 122 -126. n n 12/1/2020 The vocoder was the first synthesizer based on the analysis/re-synthesis principle – the production of speech by using the parameters obtained in the analysis phase. It was a mechanically controlled electrical speech synthesizer. It was demonstrated at the 1939 World’s Fair in New York. Veton Këpuska 109

The Vocoder Speech Synthesizer, consisting of a bank of filters excited by an impulse train or noise, and controlled by a piano-like keyboard, after Dudley et al. (1939). 12/1/2020 Veton Këpuska 110

1951 “The Pattern Playback Synthesizer” u 1951 Haskins Laboratories (Yale) “The Pattern Playback Synthesizer” n The first spectrogram driven system, and it demonstrated the acoustic significance and relevance of formant locations and their changes with time. Even though, at 1951 demonstration the pitch was kept constant at 120 Hz, it was still quite intelligible, although mechanical sounding. u http: //www. haskins. yale. edu/haskins/MISC/history. html 12/1/2020 Veton Këpuska 111

1956 PAT & OVE u 1956 The first formant synthesizers to be dynamically controlled were Walter Lawrence's Parametric Artificial Talker ("PAT") and Gunnar Fant's Orator Verbis Electris ("OVE I") (Lawrence, 1953; Fant, 1953). n n n 12/1/2020 PAT consisted of three electronic formant resonators connected in parallel, whose inputs were either a buzz or noise. A moving glass slide was used to convert painted patterns into six time functions to control the three formant frequencies, voicing amplitude, fo, and noise amplitude. OVE I, on the other hand, consisted of formant resonators connected in series, the lowest two of which were varied in frequency by movements in two dimensions of a mechanical arm. The amplitude and fo of the voicing source were determined by hand-held potentiometers. OVE I was restricted to the production of vowel-like sounds. PAT and OVE I engaged in an amusing conversation at a conference at MIT in 1956 Veton Këpuska 112

PAT & OVE u The Haskins Pattern Playback, consisting of an optical system for modulating the amplitudes of a set of harmonics of 120 Hz over time depending on patterns painted on a moving transparent belt, after Cooper et al. (1951). 12/1/2020 Veton Këpuska 113

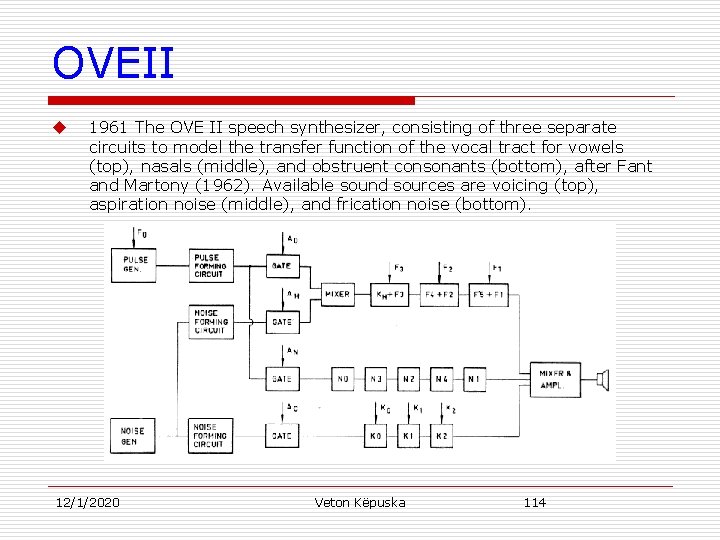
OVEII u 1961 The OVE II speech synthesizer, consisting of three separate circuits to model the transfer function of the vocal tract for vowels (top), nasals (middle), and obstruent consonants (bottom), after Fant and Martony (1962). Available sound sources are voicing (top), aspiration noise (middle), and frication noise (bottom). 12/1/2020 Veton Këpuska 114

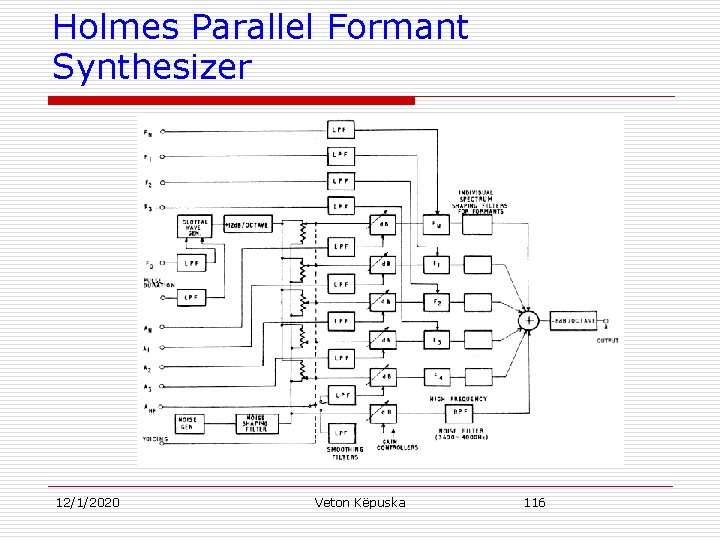
1973 Parallel Formant Synthesizer, u The Holmes parallel formant synthesizer, consisting of four parallel formants and a nasal formant, each excited by a variable mixture of voicing and/or noise, after Holmes (1973). 12/1/2020 Veton Këpuska 115

Holmes Parallel Formant Synthesizer 12/1/2020 Veton Këpuska 116

Cascade/Parallel Formant Sythesizers u 1979 MITALK u 1981 KLATTALK u 1983 DECTALK 12/1/2020 Veton Këpuska 117

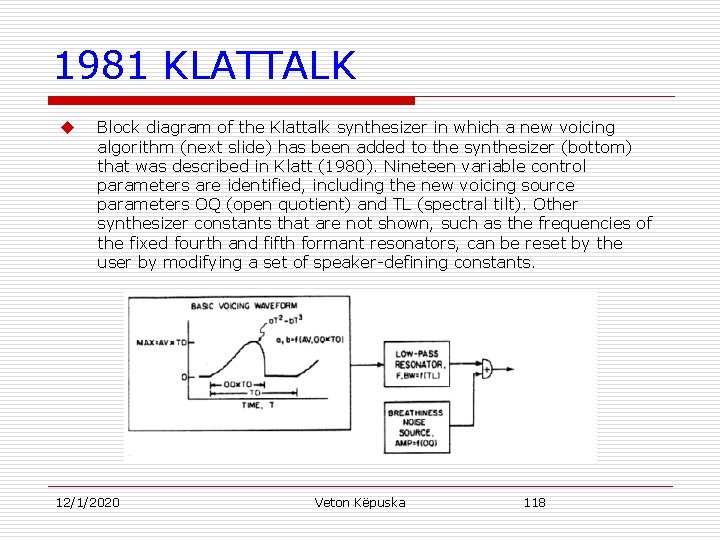
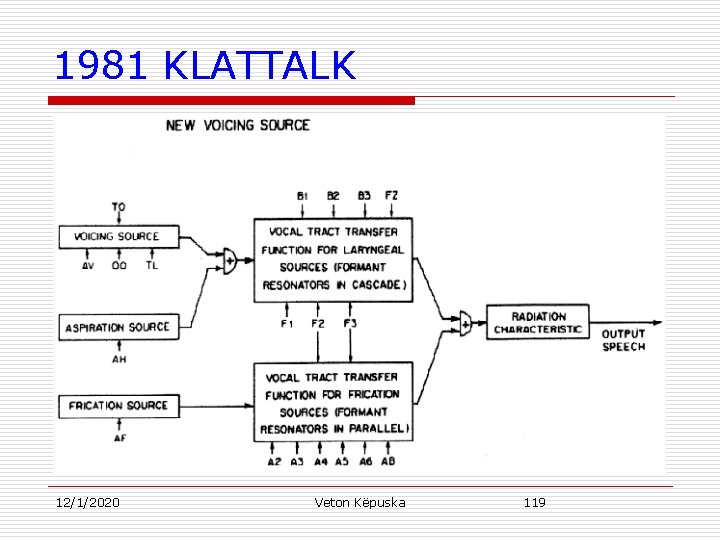
1981 KLATTALK u Block diagram of the Klattalk synthesizer in which a new voicing algorithm (next slide) has been added to the synthesizer (bottom) that was described in Klatt (1980). Nineteen variable control parameters are identified, including the new voicing source parameters OQ (open quotient) and TL (spectral tilt). Other synthesizer constants that are not shown, such as the frequencies of the fixed fourth and fifth formant resonators, can be reset by the user by modifying a set of speaker-defining constants. 12/1/2020 Veton Këpuska 118

1981 KLATTALK 12/1/2020 Veton Këpuska 119

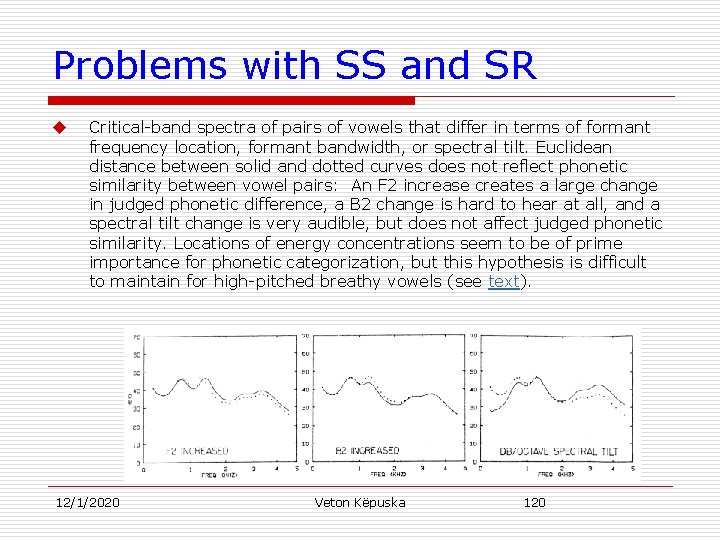
Problems with SS and SR u Critical-band spectra of pairs of vowels that differ in terms of formant frequency location, formant bandwidth, or spectral tilt. Euclidean distance between solid and dotted curves does not reflect phonetic similarity between vowel pairs: An F 2 increase creates a large change in judged phonetic difference, a B 2 change is hard to hear at all, and a spectral tilt change is very audible, but does not affect judged phonetic similarity. Locations of energy concentrations seem to be of prime importance for phonetic categorization, but this hypothesis is difficult to maintain for high-pitched breathy vowels (see text). 12/1/2020 Veton Këpuska 120

Uniform Tube Model u http: //www. haskins. yale. edu/haskins/HEADS/ASY. html Articulatory Synthesis is a method of synthesizing speech by controlling the speech articulators (e. g. jaw, tongue, lips, etc. ). This web page provides a brief overview of the Haskins Laboratories articulatory synthesis program, ASY, and related work. ASY was designed as a tool for studying the relationship between speech production and speech perception. 12/1/2020 Veton Këpuska 121

Uniform Tube Model u http: //emsah. uq. edu. au/linguistics/teaching/ling 2005/week 6 lec. html 12/1/2020 Veton Këpuska 122

Uniform Tube Model u http: //umsis. miami. edu/~kjacobso/540 p 2/project_2. htm 12/1/2020 Veton Këpuska 123

Festival Speech Synthesis Software u Project Topic: n To Port the Software to Windows n To learn to use it with existing voices n To generate a new voice u http: //www. festvox. org/ u http: //www. cstr. ed. ac. uk/projects/festival/ 12/1/2020 Veton Këpuska 124
 Alir proses produksi
Alir proses produksi Chichen itza acoustics
Chichen itza acoustics Adaptive focused acoustics
Adaptive focused acoustics Adaptive focused acoustics
Adaptive focused acoustics Room acoustics design criteria
Room acoustics design criteria Hoorzaken
Hoorzaken Perceptieslechthorendheid
Perceptieslechthorendheid Acoustics
Acoustics Lecture hall acoustic design
Lecture hall acoustic design Angelo farina
Angelo farina Wilson acoustics limited
Wilson acoustics limited Acoustics
Acoustics Acoustics graduate programs
Acoustics graduate programs Fundamentals of acoustics
Fundamentals of acoustics Ear
Ear Jd acoustics
Jd acoustics Peters uncertainty in acoustics (epub|pdf|mobi)
Peters uncertainty in acoustics (epub|pdf|mobi) Andrzej kin
Andrzej kin In-line production process eggs
In-line production process eggs Top down vs bottom up processing
Top down vs bottom up processing Gloria suarez
Gloria suarez Bottom-up processing example
Bottom-up processing example Point processing operations
Point processing operations What is primary processing of food
What is primary processing of food Point processing in image processing
Point processing in image processing Histogram processing in digital image processing
Histogram processing in digital image processing Parallel processing vs concurrent processing
Parallel processing vs concurrent processing Nonlinear image processing
Nonlinear image processing Point processing in image processing
Point processing in image processing Thinning and thickening in image processing example
Thinning and thickening in image processing example Topdown processing
Topdown processing Batch processing vs interactive processing
Batch processing vs interactive processing Modern physics vs classical physics
Modern physics vs classical physics University physics with modern physics fifteenth edition
University physics with modern physics fifteenth edition How to write a physics ia
How to write a physics ia Garrett model of speech production
Garrett model of speech production What are the 4 processes of speech production?
What are the 4 processes of speech production? Levelt's model of speech production
Levelt's model of speech production Levelt's model of speech production
Levelt's model of speech production Garrett model of speech production
Garrett model of speech production Garrett's model of speech production
Garrett's model of speech production Garrett model of speech production
Garrett model of speech production Speech production
Speech production Speech emergence stage
Speech emergence stage Match these sentences in direct and reported speech
Match these sentences in direct and reported speech What is pure speech
What is pure speech Speech to the young speech to the progress-toward
Speech to the young speech to the progress-toward Quoted speech vs reported speech
Quoted speech vs reported speech Informative speech vs persuasive
Informative speech vs persuasive Reported statements present simple
Reported statements present simple Examples of direct and indirect speech
Examples of direct and indirect speech Wh questions in indirect speech
Wh questions in indirect speech We in reported speech
We in reported speech Speech to the young speech to the progress-toward analysis
Speech to the young speech to the progress-toward analysis Structure reported speech
Structure reported speech Direct speech reported speech
Direct speech reported speech Reported speech exercises doc
Reported speech exercises doc Narration rules chart
Narration rules chart Persuasive vs informative
Persuasive vs informative Tell in reported speech
Tell in reported speech Direct speech into reported speech
Direct speech into reported speech He said i was playing football change speech
He said i was playing football change speech Direct and indirect speech worksheet
Direct and indirect speech worksheet Quoted speech to reported speech
Quoted speech to reported speech Reported speech adverbios de tiempo
Reported speech adverbios de tiempo Mass communication meaning
Mass communication meaning Production wireline and cased hole services group
Production wireline and cased hole services group What are the 4 stages of voice production?
What are the 4 stages of voice production? Virginia mason production system
Virginia mason production system Vegetable production introduction
Vegetable production introduction Drama production areas
Drama production areas Major engineering problems in urea production
Major engineering problems in urea production Practitioner myths in software engineering
Practitioner myths in software engineering A fixed input
A fixed input Lean production and quality management
Lean production and quality management Unit 4 pre-production portfolio example
Unit 4 pre-production portfolio example Filmmaking stages
Filmmaking stages Blue banana
Blue banana Flow production examples
Flow production examples 14 principles of the toyota way
14 principles of the toyota way Production function stages
Production function stages Production sheets food service
Production sheets food service Aggregate production function
Aggregate production function Cost of production
Cost of production Phases of production
Phases of production Math is not an essential skill for foodservice managers.
Math is not an essential skill for foodservice managers. Multi-camera production
Multi-camera production Television production crew
Television production crew What is all aspects of software production
What is all aspects of software production Asiatic mode of production
Asiatic mode of production Multi strand narrative
Multi strand narrative Seismic brace cable factories
Seismic brace cable factories Script breakdown example
Script breakdown example Sap pp module
Sap pp module Varun babu
Varun babu One off production definition
One off production definition Sales and operations planning
Sales and operations planning Corrected reticulocyte count formula
Corrected reticulocyte count formula Production of insulin
Production of insulin Site master file example
Site master file example Radio commercial production process
Radio commercial production process Receiving raw materials
Receiving raw materials Fab champi
Fab champi Media production architects
Media production architects Three stages of short run production function
Three stages of short run production function Production rules examples
Production rules examples Production support process
Production support process Hydrogen production from biomass ppt
Hydrogen production from biomass ppt Nslp production record template
Nslp production record template Production record
Production record Operational readiness review template
Operational readiness review template Creating production possibilities schedules and curves
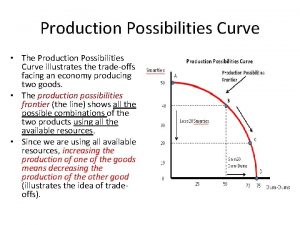
Creating production possibilities schedules and curves Production possibilities curve illustrates
Production possibilities curve illustrates Production planning and inventory control
Production planning and inventory control Meaning of production planning and control
Meaning of production planning and control Production process in theatre
Production process in theatre What is productivity
What is productivity Production is the creation of
Production is the creation of Production, information costs, and economic organization
Production, information costs, and economic organization Production function
Production function Production finale
Production finale Three stages of production function
Three stages of production function Production cycle flowchart
Production cycle flowchart Average product of labor
Average product of labor Production definition
Production definition