SPECTROSCOPY OF COLD MOLECULES PRODUCED BY VELOCITY FILTERING

SPECTROSCOPY OF COLD MOLECULES PRODUCED BY VELOCITY FILTERING Daisuke Ando, * Susumu Kuma, ** Masaaki Tsubouchi, ** and Takamasa Momose** *Kyoto University, JAPAN **The University of British Columbia, CANADA

What is “Cold molecules”? Both internal and translational energies (TE) are cold. Supersonic expansion Internal energies O TE in Lab. frame X very difficult By using slow molecules… 1. Ultra high precision spectroscopy Spectroscopy of bio-molecules Detection of internal dynamics from linewidth 2. Reaction dynamics in low temperature collision Interference of de Broglie wave Resonances at the intermediate state h fast t slow t

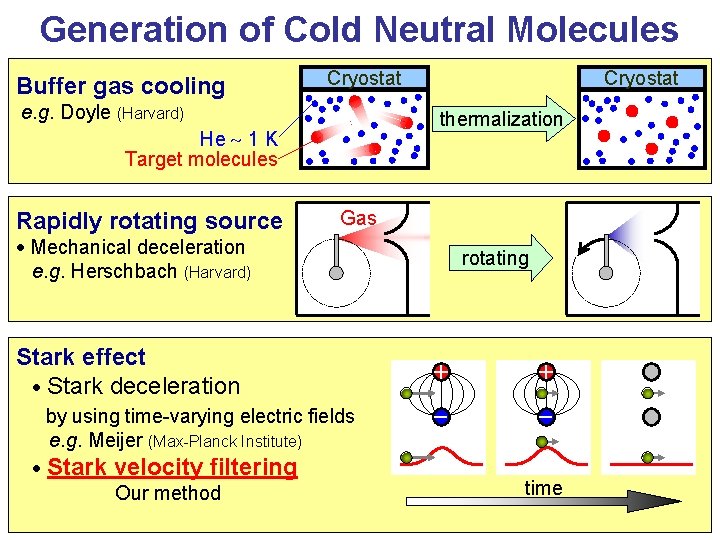
Generation of Cold Neutral Molecules Buffer gas cooling Cryostat e. g. Doyle (Harvard) thermalization He 1 K Target molecules Rapidly rotating source Cryostat Gas Mechanical deceleration e. g. Herschbach (Harvard) Stark effect Stark deceleration by using time-varying electric fields e. g. Meijer (Max-Planck Institute) Stark velocity filtering Our method rotating + + - time

Purpose of this Study Generation of slow molecules by Stark velocity filtering technique Observation of cold Molecules by LIF Spectroscopy

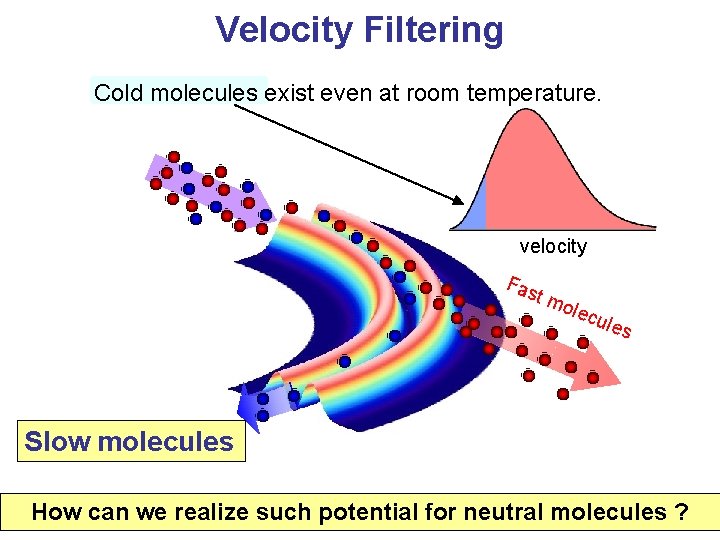
Velocity Filtering Cold molecules exist even at room temperature. velocity Fas tm olec ules Slow molecules How can we realize such potential for neutral molecules ?

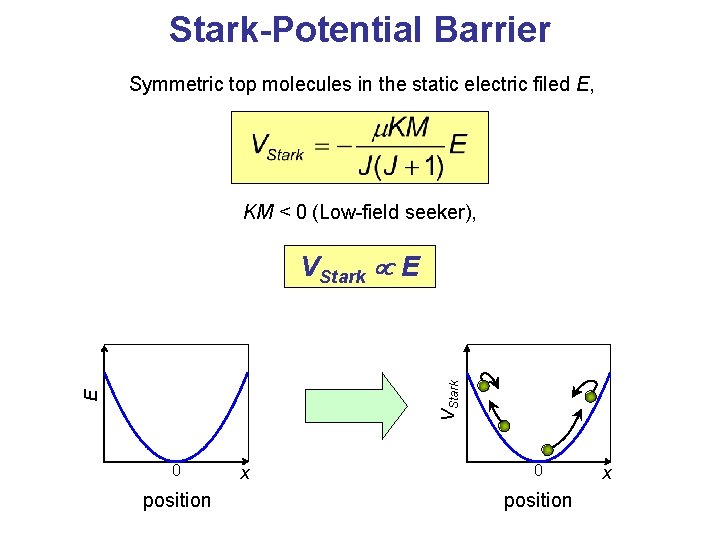
Stark-Potential Barrier Symmetric top molecules in the static electric filed E, KM < 0 (Low-field seeker), E VStark E 0 position x

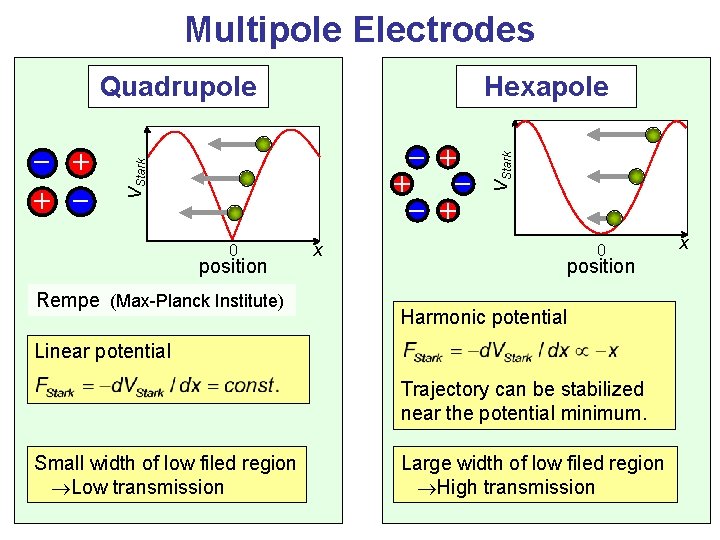
Multipole Electrodes - + + - + VStark - + + - Hexapole 0 position Rempe (Max-Planck Institute) x VStark Quadrupole 0 position Harmonic potential Linear potential Trajectory can be stabilized near the potential minimum. Small width of low filed region Low transmission Large width of low filed region High transmission x

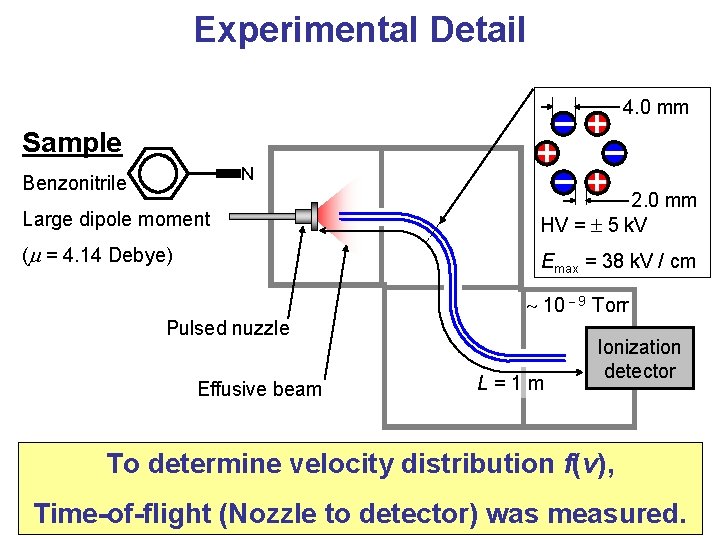
Experimental Detail 4. 0 mm Sample N Benzonitrile - + + - + Large dipole moment 2. 0 mm HV = 5 k. V ( = 4. 14 Debye) Emax = 38 k. V / cm Pulsed nuzzle Effusive beam 10 - 9 Torr L=1 m Ionization detector To determine velocity distribution f(v), Time-of-flight (Nozzle to detector) was measured.

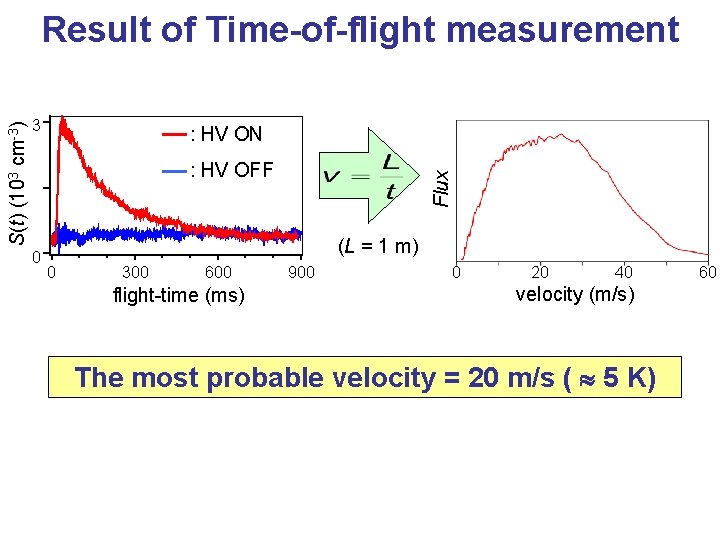
3 : HV ON : HV OFF 0 Flux S(t) (103 cm-3) Result of Time-of-flight measurement (L = 1 m) 0 300 600 flight-time (ms) 900 0 20 40 velocity (m/s) The most probable velocity = 20 m/s ( 5 K) 60

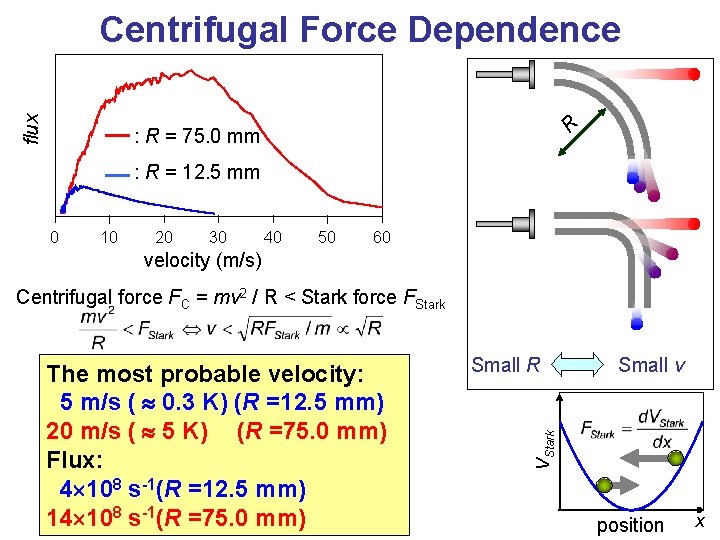
R flux Centrifugal Force Dependence : R = 75. 0 mm : R = 12. 5 mm 0 10 20 30 40 50 60 velocity (m/s) Centrifugal force FC = mv 2 / R < Stark force FStark Small R Small v VStark The most probable velocity: 5 m/s ( 0. 3 K) (R =12. 5 mm) 20 m/s ( 5 K) (R =75. 0 mm) Flux: 4 108 s-1(R =12. 5 mm) 14 108 s-1(R =75. 0 mm) position x

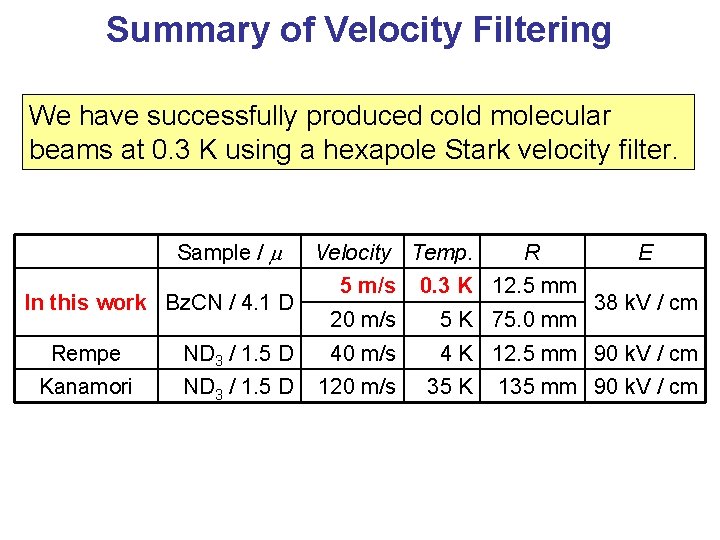
Summary of Velocity Filtering We have successfully produced cold molecular beams at 0. 3 K using a hexapole Stark velocity filter. Sample / In this work Bz. CN / 4. 1 D Velocity Temp. R E 5 m/s 0. 3 K 12. 5 mm 20 m/s 5 K 75. 0 mm 4 K 12. 5 mm 90 k. V / cm Rempe ND 3 / 1. 5 D 40 m/s Kanamori ND 3 / 1. 5 D 120 m/s 35 K 38 k. V / cm 135 mm 90 k. V / cm

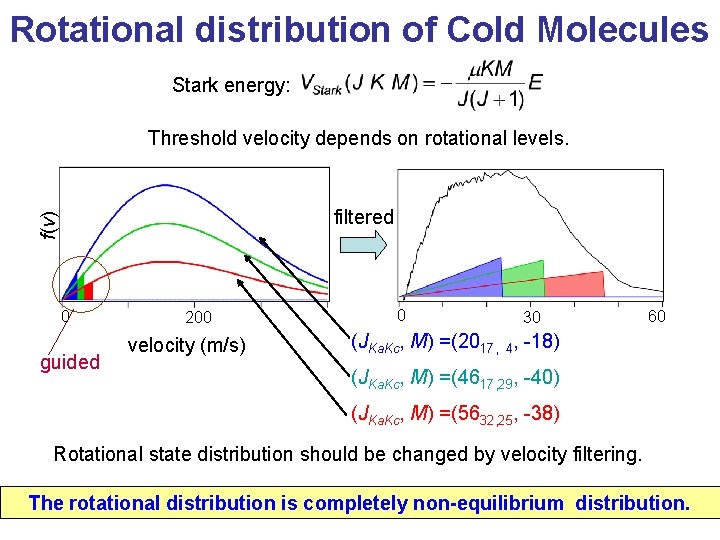
Rotational distribution of Cold Molecules Stark energy: Threshold velocity depends on rotational levels. f(v) filtered 0 guided 200 velocity (m/s) 0 30 60 (JKa. Kc, M) =(2017, 4, -18) (JKa. Kc, M) =(4617, 29, -40) (JKa. Kc, M) =(5632, 25, -38) Rotational state distribution should be changed by velocity filtering. The rotational distribution is completely non-equilibrium distribution.

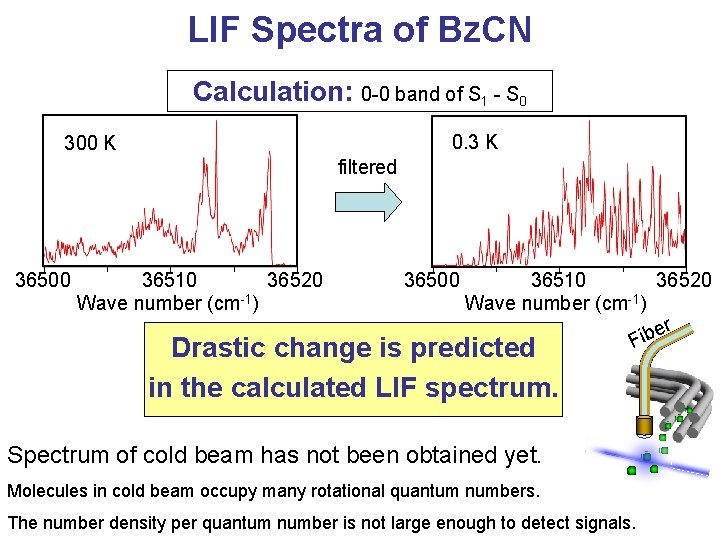
LIF Spectra of Bz. CN Calculation: 0 -0 band of S 1 - S 0 0. 3 K 300 K filtered 36500 36510 36520 Wave number (cm-1) er b i F predicted Drastic change is in the calculated LIF spectrum. Spectrum of cold beam has not been obtained yet. Molecules in cold beam occupy many rotational quantum numbers. The number density per quantum number is not large enough to detect signals.

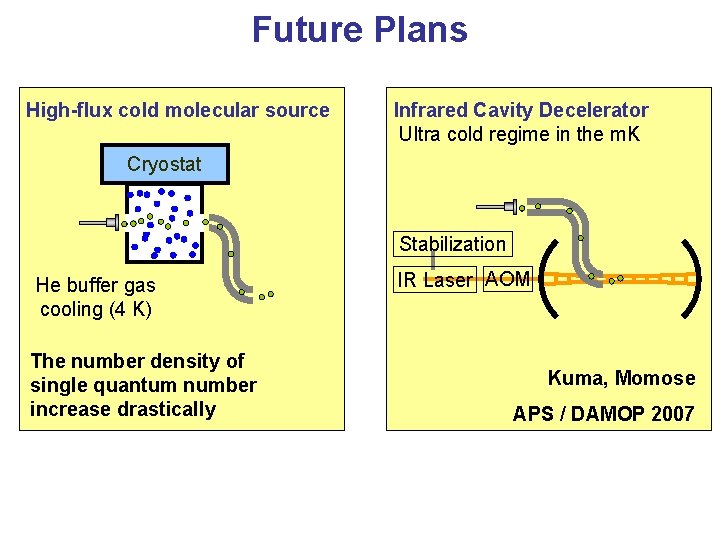
Future Plans High-flux cold molecular source Infrared Cavity Decelerator Ultra cold regime in the m. K Cryostat Stabilization He buffer gas cooling (4 K) The number density of single quantum number increase drastically IR Laser AOM Kuma, Momose APS / DAMOP 2007

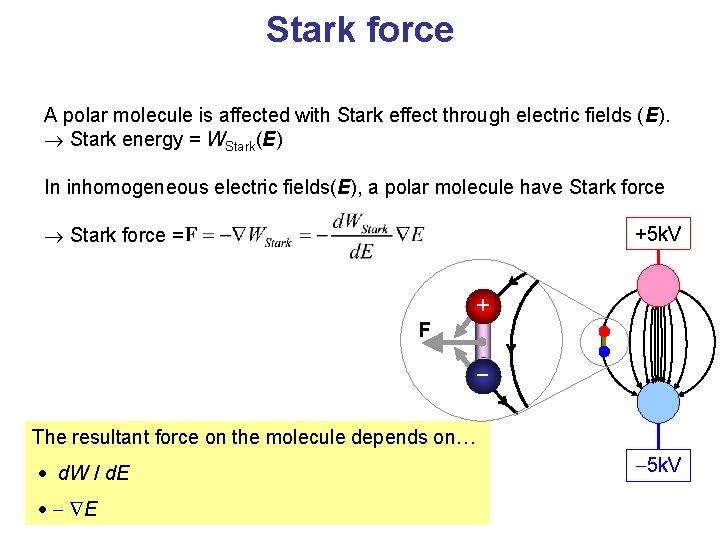
Stark force A polar molecule is affected with Stark effect through electric fields (E). Stark energy = WStark(E) In inhomogeneous electric fields(E), a polar molecule have Stark force = +5 k. V + F - The resultant force on the molecule depends on… d. W / d. E - E -5 k. V

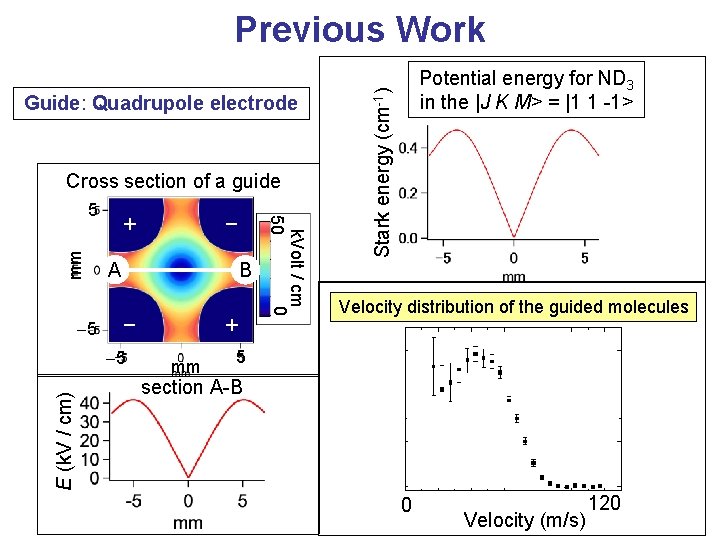
Previous Work Cross section of a guide mm -5 + A B - -5 E (k. V / cm) - + mm k. Volt / cm 0 50 5 Stark energy (cm-1) Guide: Quadrupole electrode Potential energy for ND 3 in the |J K M> = |1 1 -1> Velocity distribution of the guided molecules 5 section A-B 0 Velocity (m/s) 120

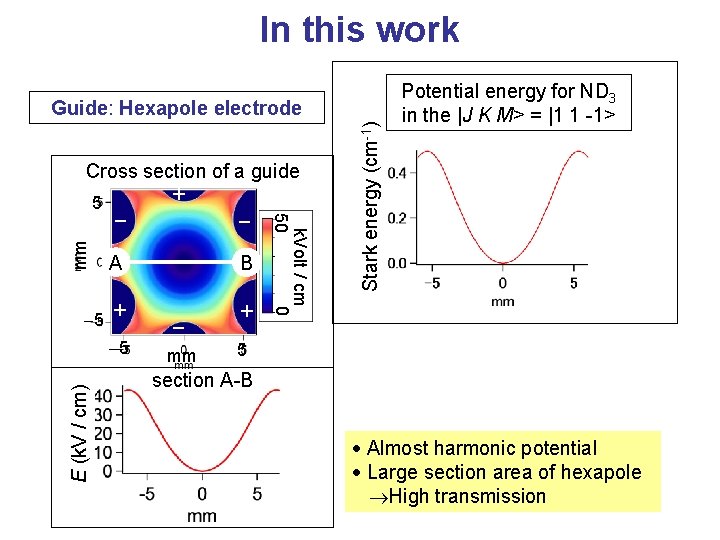
In this work mm -5 A B + + E (k. V / cm) -5 mm k. Volt / cm 0 50 Cross section of a guide + 5 - Stark energy (cm-1) Guide: Hexapole electrode Potential energy for ND 3 in the |J K M> = |1 1 -1> 5 section A-B Almost harmonic potential Large section area of hexapole High transmission

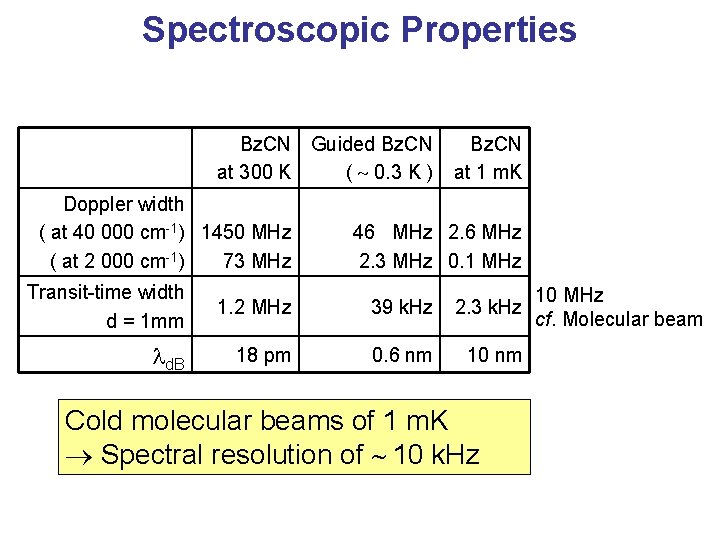
Spectroscopic Properties Bz. CN Guided Bz. CN at 300 K ( 0. 3 K ) Doppler width ( at 40 000 cm-1) 1450 MHz ( at 2 000 cm-1) 73 MHz Bz. CN at 1 m. K 46 MHz 2. 3 MHz 0. 1 MHz Transit-time width d = 1 mm 1. 2 MHz 39 k. Hz 2. 3 k. Hz d. B 18 pm 0. 6 nm 10 nm Cold molecular beams of 1 m. K Spectral resolution of 10 k. Hz 10 MHz cf. Molecular beam

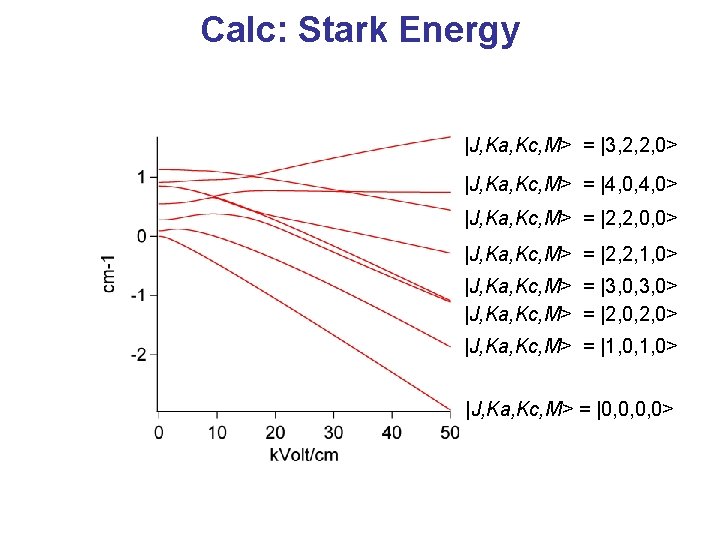
Calc: Stark Energy |J, Ka, Kc, M> = |3, 2, 2, 0> |J, Ka, Kc, M> = |4, 0, 4, 0> |J, Ka, Kc, M> = |2, 2, 0, 0> |J, Ka, Kc, M> = |2, 2, 1, 0> |J, Ka, Kc, M> = |3, 0, 3, 0> |J, Ka, Kc, M> = |2, 0, 2, 0> |J, Ka, Kc, M> = |1, 0, 1, 0> |J, Ka, Kc, M> = |0, 0, 0, 0>