Spectroscopy l Microwave Rotational l Infrared Vibrational l

Spectroscopy l Microwave (Rotational) l Infrared (Vibrational) l Raman (Rotational & Vibrational) l Texts – “Physical Chemistry”, 6 th edition, Atkins – “Fundamentals of Molecular Spectroscopy”, 4 th edition, Banwell & Mc. Cash 1

Introduction-General Principles Spectra - transitions between energy states Molecule, Ef - Ei = hu photon Transition probability – selection rules l Populations (Boltzmann distribution) – number of molecules in level j at equilibrium l 2

Typical energies 3

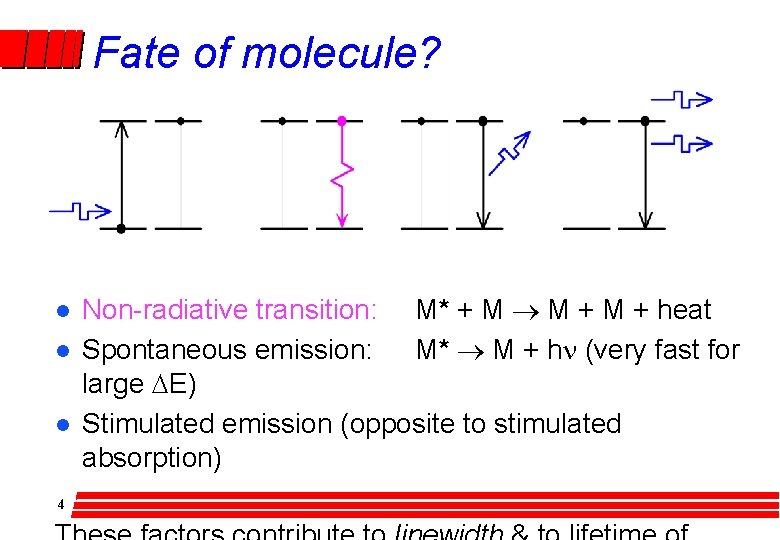
Fate of molecule? l l l 4 Non-radiative transition: M* + M ® M + heat Spontaneous emission: M* ® M + hn (very fast for large DE) Stimulated emission (opposite to stimulated absorption)

MCWE or Rotational Spectroscopy Classification of molecules l Based on moments of inertia, I=mr 2 – – 5 IA ¹ IB ¹ IC IA = IB = I C IA ¹ IB = IC IA = 0, IB = IC very complex eg H 2 O no MCWE spectrum eg CH 4 complicated eg NH 3 linear molecules eg Na. Cl

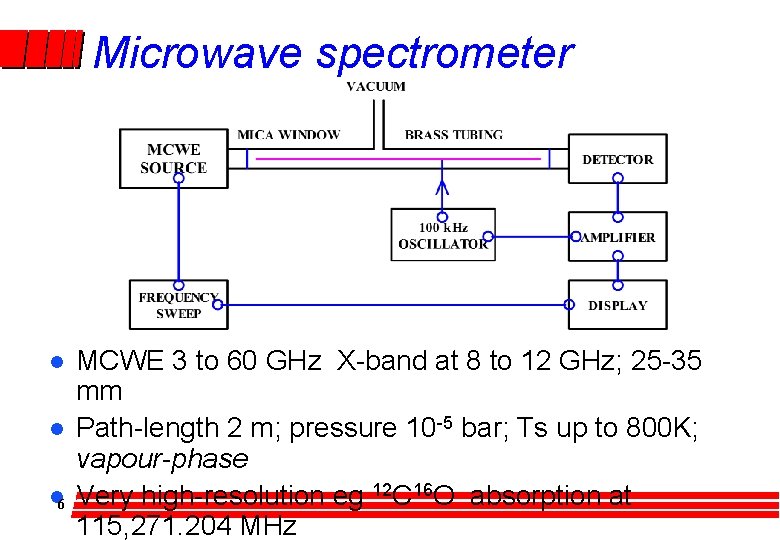
Microwave spectrometer l l l 6 MCWE 3 to 60 GHz X-band at 8 to 12 GHz; 25 -35 mm Path-length 2 m; pressure 10 -5 bar; Ts up to 800 K; vapour-phase Very high-resolution eg 12 C 16 O absorption at 115, 271. 204 MHz

Rotating diatomic molecule l Degeneracy of Jth level is (2 J+1) l Selection rules for absorption are: l Compounds must be in the vapour-phase á DJ = +1 á The molecule must have a non-zero dipole moment, p ¹ 0. So N 2 etc do not absorb microwave radiation. – But it is easy to work at temperatures up to 800 K since cell is made of brass with mica windows. Even solid Na. Cl has sufficient vapour pressure to give a good spectrum. 7

Rotational energy levels For DJ=1 l DE = 2 ( J+1) h 2/8 p 2 I 0® 1 DE = 2 h 2/8 p 2 I 1® 2 DE = 4 h 2/8 p 2 I 2® 3 DE = 6 h 2/8 p 2 I etc. , etc. Constant difference of: l DE = 2 h 2/8 p 2 I 8

Populations of rotational levels 9

Example Pure MCWE absorptions at 84. 421 , 90. 449 and 96. 477 GHz on flowing dibromine gas over hot copper metal at 1100 K. What transitions do these frequencies represent? Note: 96. 477 - 90. 449 = 6. 028 and also 90. 449 - 84. 421 = 6. 028 l So, constant diff. of 6. 028 GHz or 6. 028´ 109 s-1. DE = 2 h 2/8 p 2 I = h (6. 028´ 109 s-1) l So 84. 421 ¸ 6. 028 = 14. 00 ie J=13 ® J=14 l & 90. 449 ¸ 6. 028 = 15 ie J=14 ® J=15 l & 96. 477 ¸ 6. 028 = 16 ie J=15 ® J=16 10 l

Moment of inertia, I DE = 2 h 2/8 p 2 I = hv = h(6. 028´ 109 s-1) I = 2 h/(8 p 2 6. 028´ 109 ) l I = 2 (6. 626´ 10 -34)/(8 p 2 6. 028´ 109 ) I = 2. 784´ 10 -45 Units? Þ (J s)/(s-1) = J s 2 = kg m 2 s-2 s 2 = kg m 2 But I = mr 2 l m = (0. 063´ 0. 079)/(0. 063+0. 079)NA = 5. 82´ 10 -26 kg l 11 Þ r = Ö(I/m) = 218. 6´ 10 -12 m = 218. 6 pm

Emission spectroscopy? l Radio-telescopes pick up radiation from interstellar space. High resolution means that species can be identified unambiguously. Owens Valley Radio Observatory 10. 4 m telescope l Orion A molecular cloud » 300 K, » 10 -7 cm-3 517 lines from 25 species CN, Si. O, SO 2, H 2 CO, OCS, CH 3 OH, etc l 12 13 CO (220, 399 MHz) and 12 CO (230, 538 MHz)

IR / Vibrational spectroscopy = (v + 1/2) (h/2 p) (k/m)1/2 l v = 0, 1, 2, 3, … l Ev Selection rules: Þ Dv = 1 & p must change during vibration Let we = wavenumber of transition then “energy”: Þ ev = (v + 1/2) we l Untrue for real molecules since parabolic potential does not allow for bond breaking. Þ ev = (v + 1/2) we - (v + 1/2)2 we xe – where xe is the anharmonicity constant 13

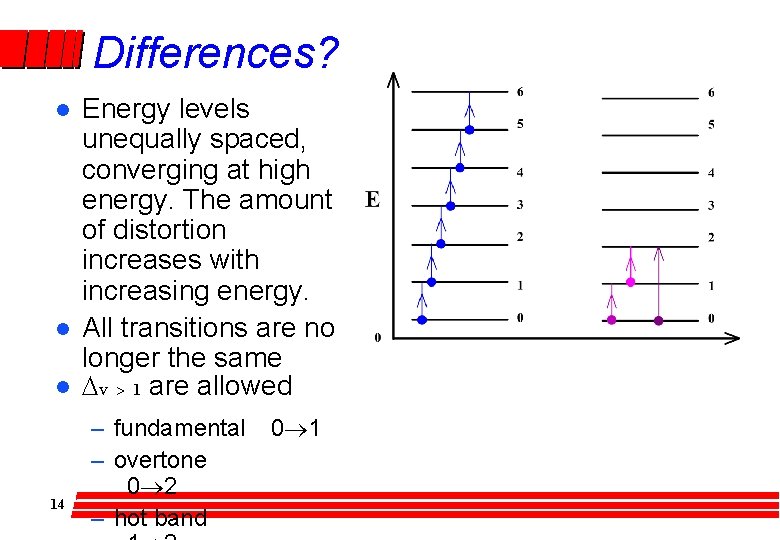
Differences? l l l 14 Energy levels unequally spaced, converging at high energy. The amount of distortion increases with increasing energy. All transitions are no longer the same Dv > 1 are allowed – fundamental – overtone 0® 2 – hot band 0® 1

Example HCl has a fundamental band at 2, 885. 9 cm-1, and an overtone at 5, 668. 1 cm-1. Calculate we and the anharmonicity constant xe. l ev = (v + 1/2) we - (v + 1/2)2 we xe ¨ e 2 = (2 + 1/2) we - (2 + 1/2)2 we xe ¨ e 1 = (1 + 1/2) we - (1 + 1/2)2 we xe ¨ e 0 = (0 + 1/2) we - (0 + 1/2)2 we xe ¨ e 2 - e 0 = 2 we - 6 we xe= 5, 668. 1 ¨ e 1 - e 0 = we - 2 we xe= 2, 885. 9 Å we = 2, 989. 6 cm-1 we xe = 51. 9 cm-1 15 xe = 0. 0174

High resolution infrared Ev = (v + 1/2) (h/2 p) (k/m)1/2 ev = (v + 1/2) we EJ = J(J+1) (h 2/8 I) e. J = J(J + 1) Bv Vibrational + rotational energy changes l e(v, J) = (v + 1/2) we + J(J + 1) Bv l Selection rule: Dv=+1, DJ=± 1 – Rotational energy change must accompany a vibrational energy change. 16

Vibrational + rotational changes in the IR 17

Hi-resolution spectrum of HCl l 18 Above the “gap”; DJ = +1 Below the “gap”: DJ = – 1 Intensities mirror populations of starting levels

Example: HBr Lines at … 2590. 95, 2575. 19, 2542. 25, 2525. 09, . . . cm-1 l Difference is roughly 15 except between 2 nd & 3 rd where it is double this. Hence, missing transition lies around 2560 cm-1. So 2575 is (v=0, J=0) ® (v=1, J=1) & 2590 is (v=0, J=1) ® (v=1, J=2) So 2542 is (v=0, J=1) ® (v=1, J=0) & 2525 is (v=0, J=2) ® (v=1, J=1) (2575. 19 - 2525. 25) = 6 B 0 B 0=8. 35 cm-1 -1 (2590. 95 2542. 25) = 6 B B =8. 12 cm 1 1 19 -1

Raman spectroscopy l l 20 Different principles. Based on scattering of (usually) visible monochromatic light by molecules of a gas, liquid or solid Two kinds of scattering encountered: – Rayleigh (1 in every 10, 000) – Raman (1 in every 10, 000) frequencies same frequency different

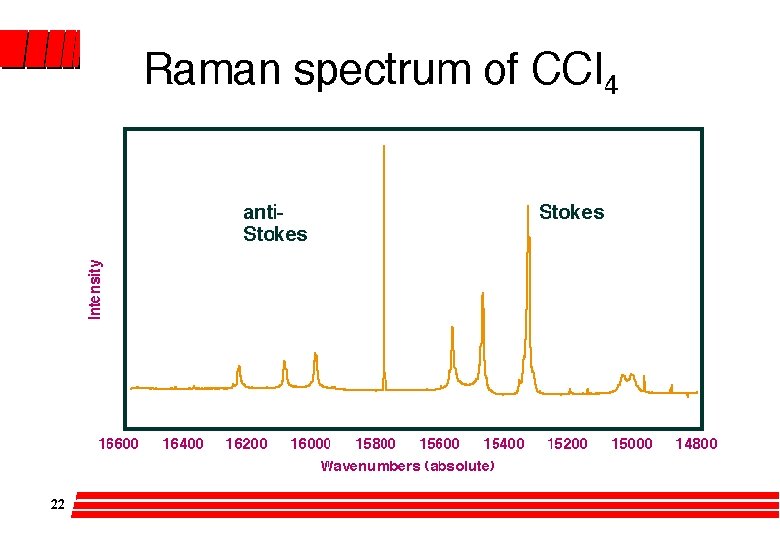
Raman l Light source? Laser – Monochromatic, Highly directional, Intense He-Ne 633 nm or Argon ion 488, 515 nm Cells? Glass or quartz; so aqueous solutions OK l Form of emission spectroscopy l Spectrum highly symmetrical eg for liquid CCl 4 21 there are peaks at ± 218, ± 314 and ± 459 cm-1 shifted from the original incident radiation at 633 nm (15, 800 cm-1). » The lower wavenumber side or Stokes radiation tends

22

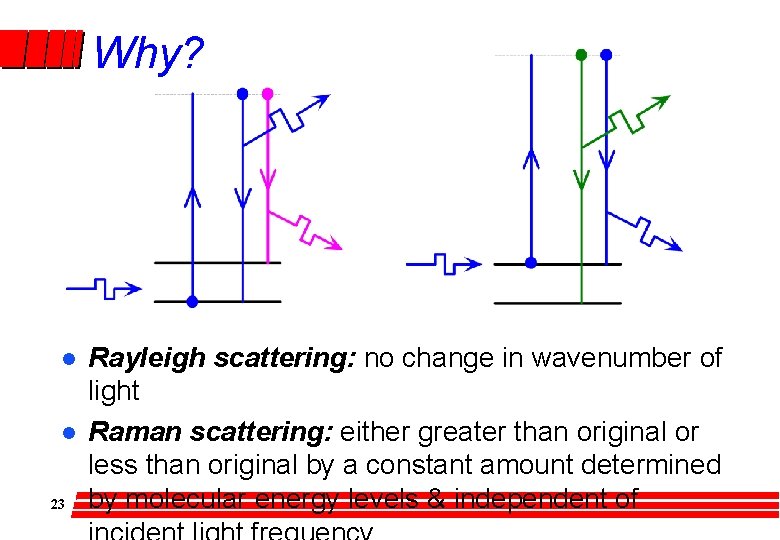
Why? l l 23 Rayleigh scattering: no change in wavenumber of light Raman scattering: either greater than original or less than original by a constant amount determined by molecular energy levels & independent of

Raman selection rules l Vibrational energy levels – Dv = ± 1 – Polarisability must change during particular vibration l Rotational energy levels – DJ = ± 2 – Non-isotropic polarisability (ie molecule must not be spherically symmetric like CH 4, SF 6, etc. ) l 24 Combined

Vibrational Raman l l Symmetric stretching vibration of CO 2 Polarisability changes – therefore Raman band at 1, 340 cm-1 l Dipole moment does not – no absorption at 1, 340 cm-1 in IR 25

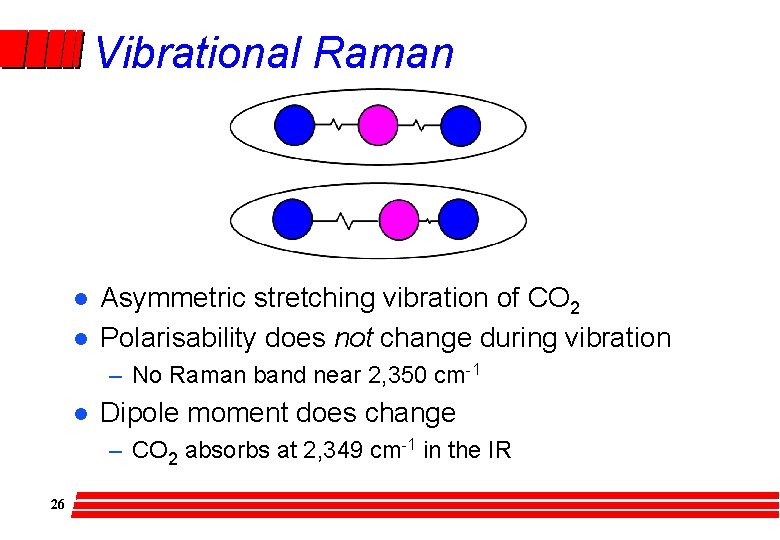
Vibrational Raman l l Asymmetric stretching vibration of CO 2 Polarisability does not change during vibration – No Raman band near 2, 350 cm-1 l Dipole moment does change – CO 2 absorbs at 2, 349 cm-1 in the IR 26

Example In an experiment jets of argon gas and tin vapour impinged on a metal block cooled to 12 K in vacuo. The Raman spectrum of the frozen matrix showed a series of peaks beginning at 187 cm-1 and with diminishing intensity at 373, 558, 743, etc cm-1. What species is responsible for the observed spectrum? l Shifts of ca. 200 cm-1 indicate vibrational energies; diatomic tin? Is 187 the fundamental? With the second peak at 373 (note 2 x 187 = 374), the third at 558 being 3 x 187 = 561, etc. Use ev = (v + 1/2) we - (v + 1/2)2 we xe l l 27 Substitute in v=0, v=1, v=2, etc then compute:

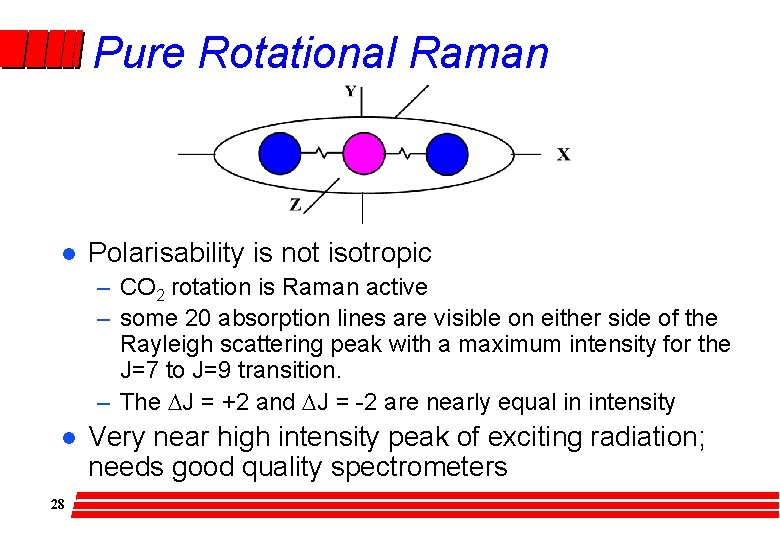
Pure Rotational Raman l Polarisability is not isotropic – CO 2 rotation is Raman active – some 20 absorption lines are visible on either side of the Rayleigh scattering peak with a maximum intensity for the J=7 to J=9 transition. – The DJ = +2 and DJ = -2 are nearly equal in intensity l 28 Very near high intensity peak of exciting radiation; needs good quality spectrometers

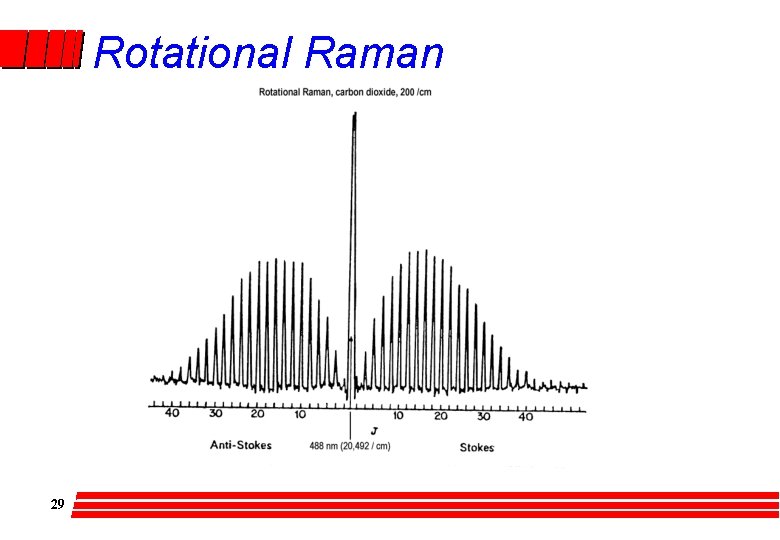
Rotational Raman 29

Raman applications l Structure of Hg(I) in aqueous solution – Is it Hg+ ? or (Hg 2)2+ ? – Aqueous solutions of Hg. NO 3 show Raman band at 169 cm-1 (as well as NO 3 - bands), solid Hg. Cl shows a 30 band at 167 cm-1 – Conclusion: Hg(I) exists as a diatomic cation (note that a symmetrical diatomic would vibrate but would not absorb in the IR; different selection rule) – Very little sample preparation required; easy to get good quality spectra of: solids, powders, fibers, crystals – Drawbacks: coloured samples may overheat &

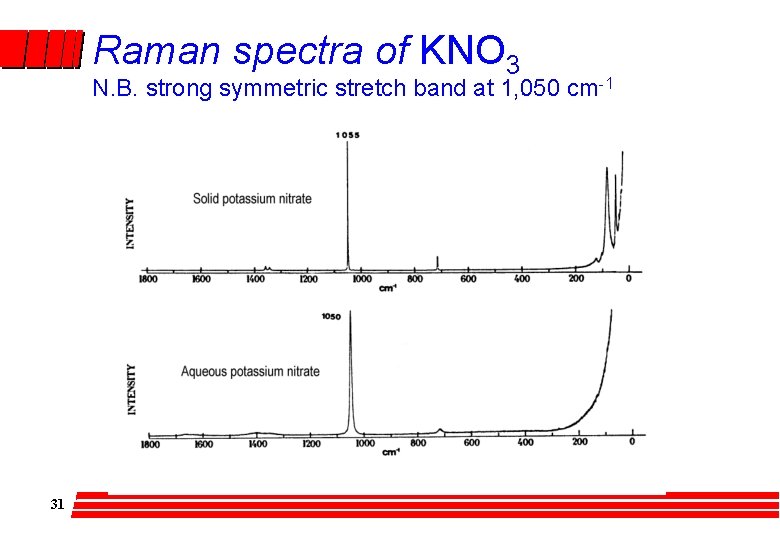
Raman spectra of KNO 3 N. B. strong symmetric stretch band at 1, 050 cm-1 31

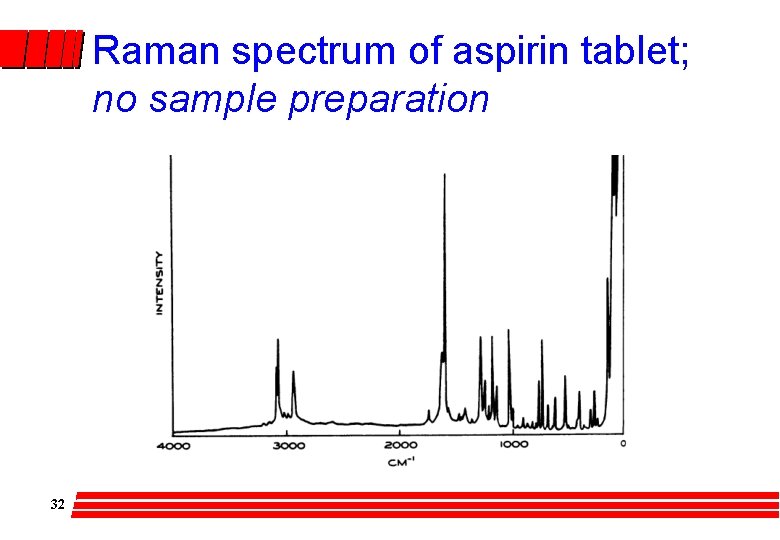
Raman spectrum of aspirin tablet; no sample preparation 32

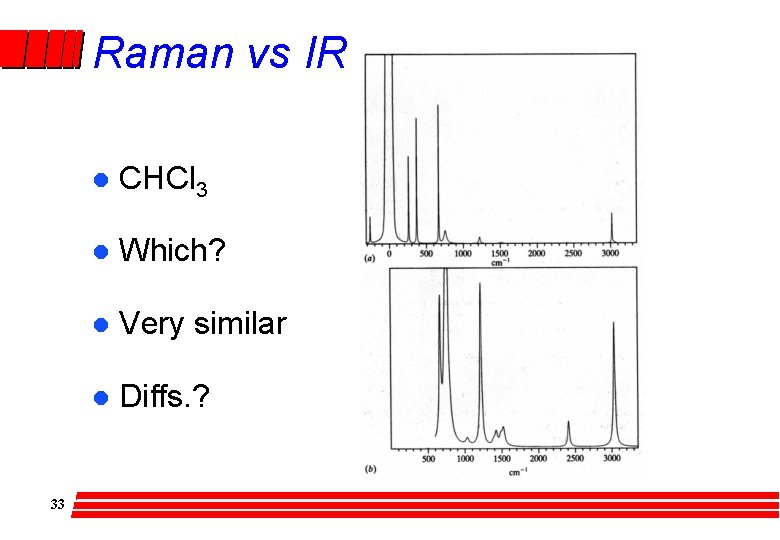
Raman vs IR 33 l CHCl 3 l Which? l Very similar l Diffs. ?