Spectroscopy and Electron Configurations Light is an electromagnetic

Spectroscopy and Electron Configurations

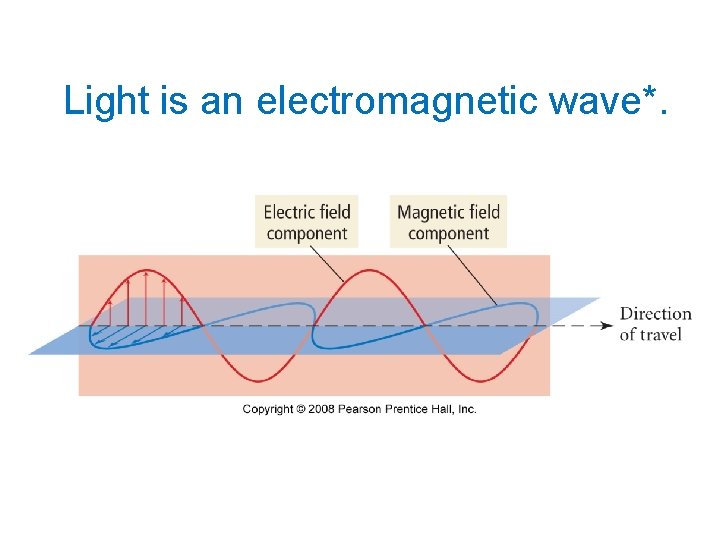
Light is an electromagnetic wave*.

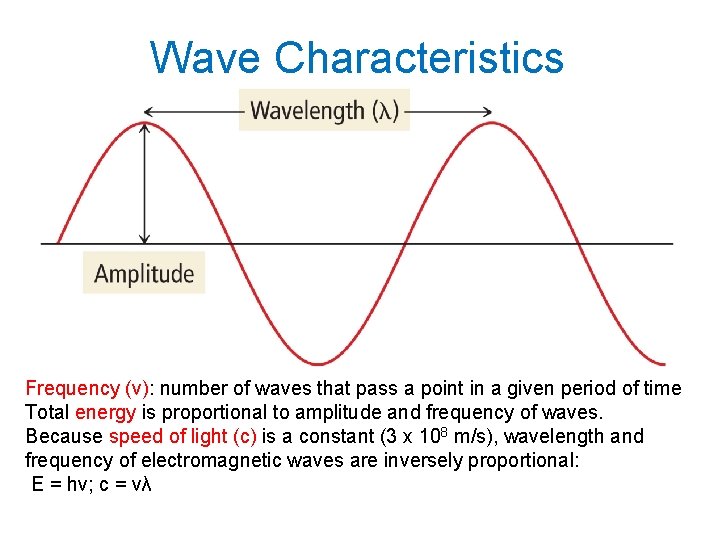
Wave Characteristics Frequency (ν): number of waves that pass a point in a given period of time Total energy is proportional to amplitude and frequency of waves. Because speed of light (c) is a constant (3 x 108 m/s), wavelength and frequency of electromagnetic waves are inversely proportional: E = hν; c = νλ

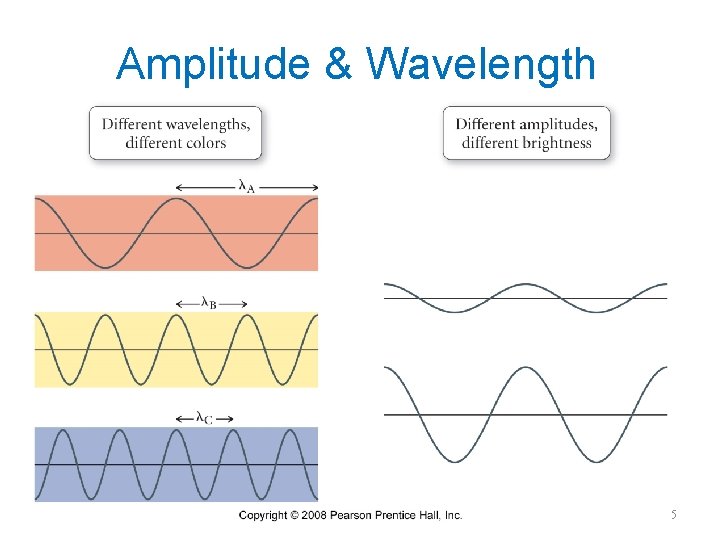
Color White light is composed of all colors which can be separated into a rainbow, or a spectrum, by passing the light through a prism. Each color light has a different wavelength, and, therefore, frequency.

Amplitude & Wavelength 5

Are there other “Colors”?

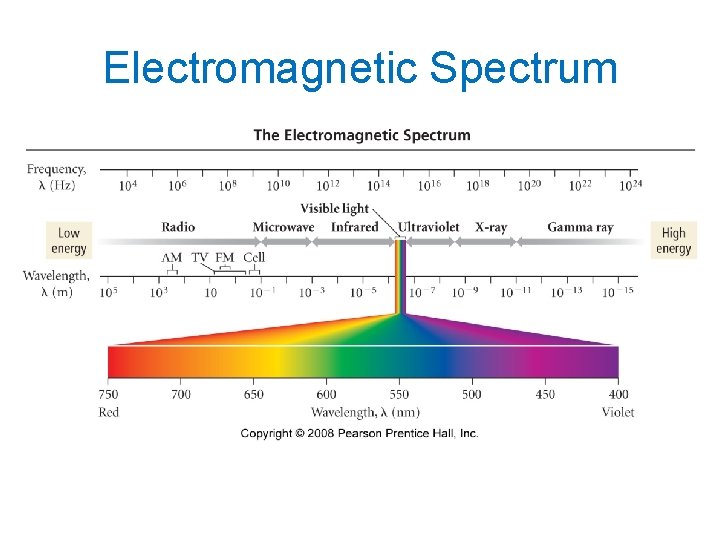
The Electromagnetic Spectrum • Visible light comprises only a small fraction of all the wavelengths of light – called the electromagnetic spectrum. • Short wavelength (high frequency) light has high energy. - Gamma ray light has the highest energy. • Long wavelength (low frequency) light has low energy. - Radiowave light has the lowest energy.

Electromagnetic Spectrum

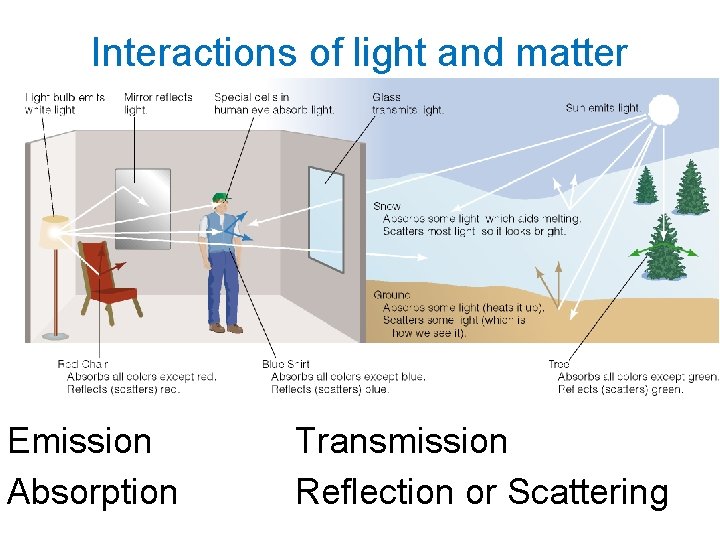
Interactions of light and matter Emission Absorption Transmission Reflection or Scattering

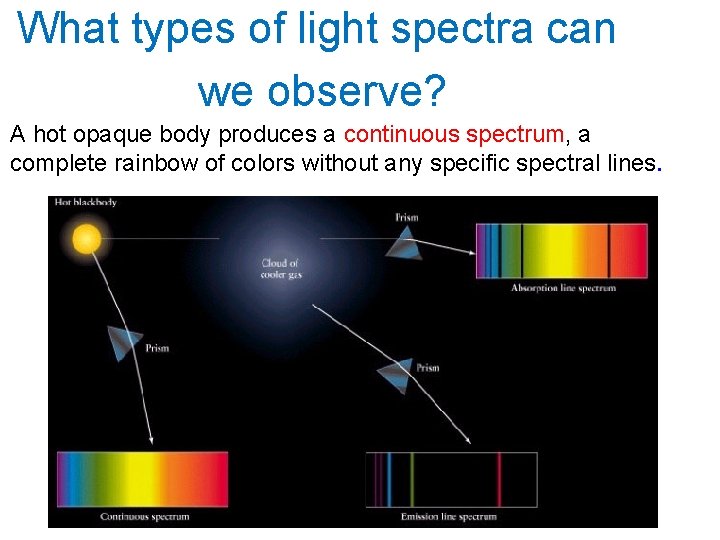
What types of light spectra can we observe? A hot opaque body produces a continuous spectrum, a complete rainbow of colors without any specific spectral lines.

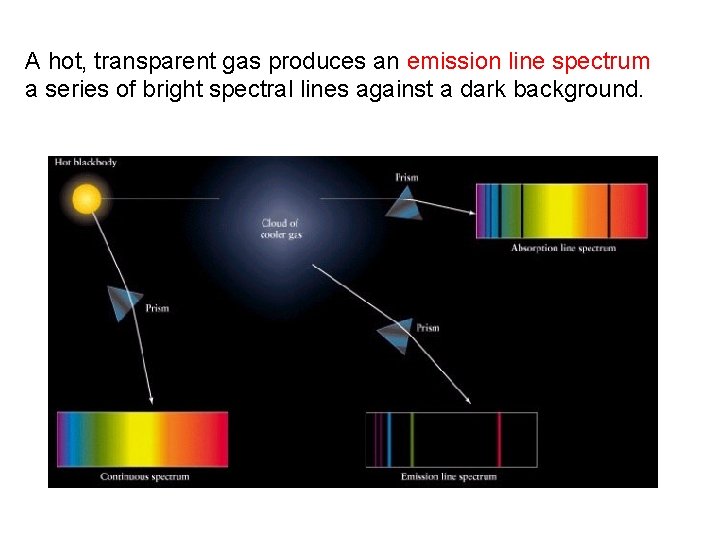
A hot, transparent gas produces an emission line spectrum a series of bright spectral lines against a dark background.

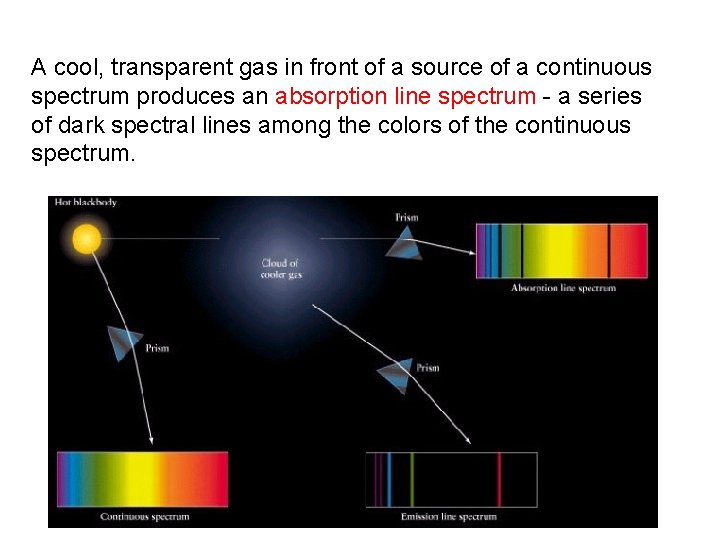
A cool, transparent gas in front of a source of a continuous spectrum produces an absorption line spectrum - a series of dark spectral lines among the colors of the continuous spectrum.

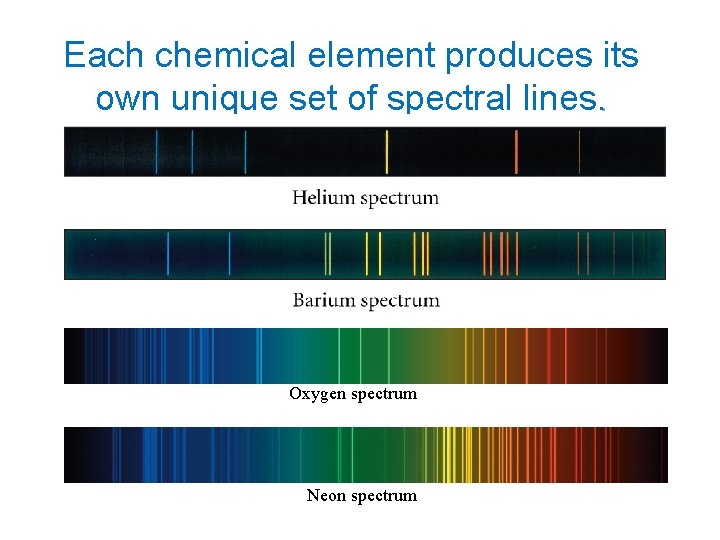
Each chemical element produces its own unique set of spectral lines. Oxygen spectrum Neon spectrum

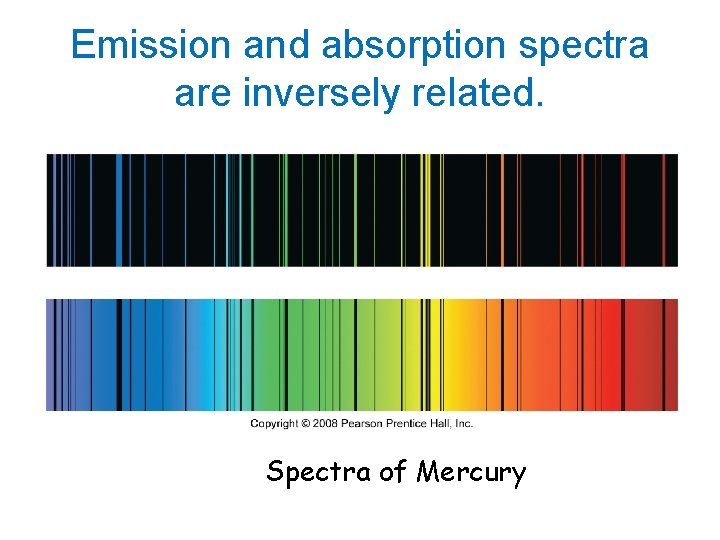
Emission and absorption spectra are inversely related. Spectra of Mercury

Identifying Elements with Flame Tests Na K Li Ba

Exciting Gas Atoms to Emit Light with Electrical Energy Hg He H

Analyzing the Hydrogen Emission Spectrum Rydberg found the spectrum of hydrogen could be described with an equation that involved an inverse square of integers.

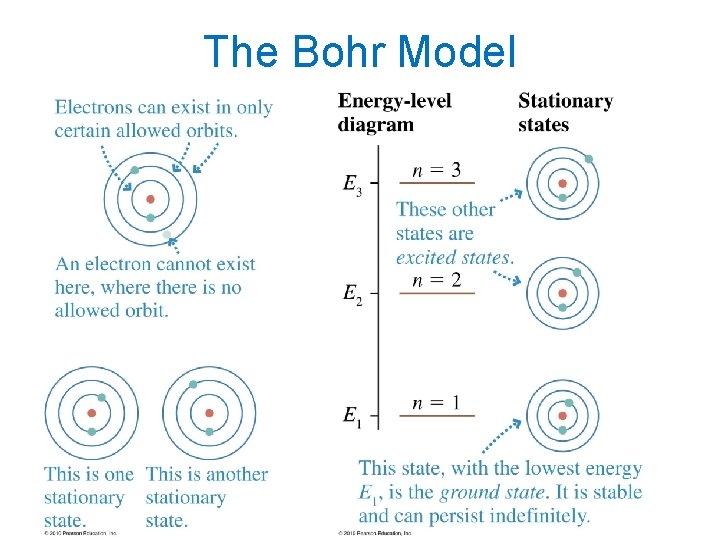
Bohr Model of Hydrogen Atom e- In the Bohr model, electrons: - have quantized energies. - have orbits a fixed distance from the nucleus.

The Bohr Model

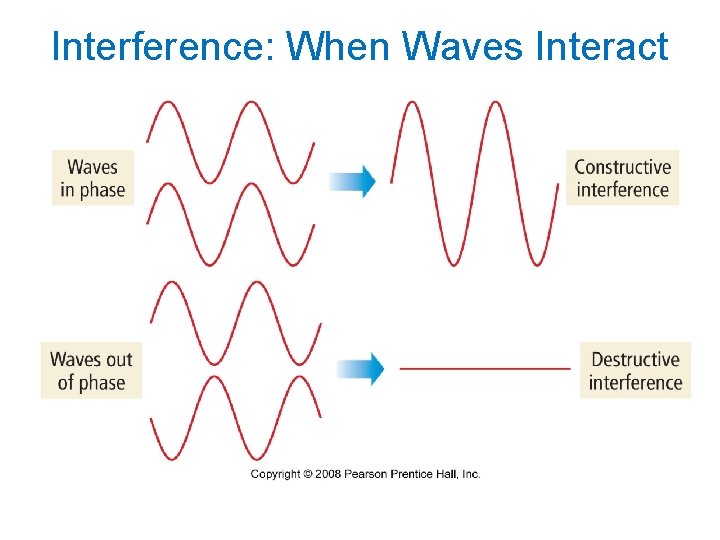
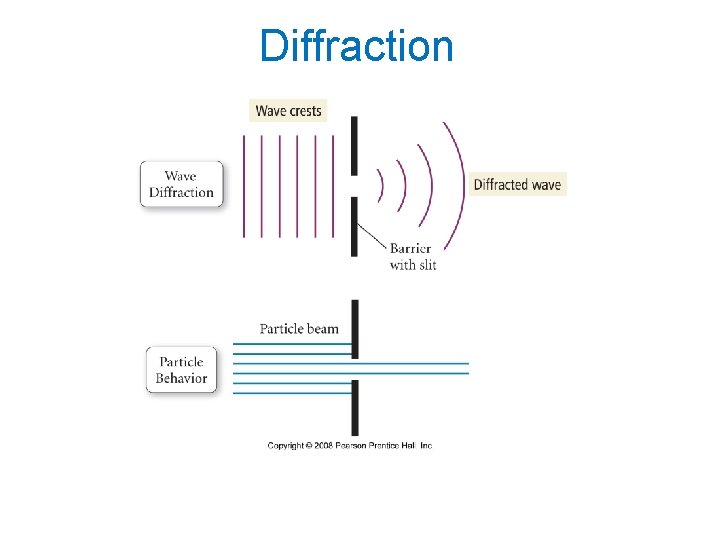
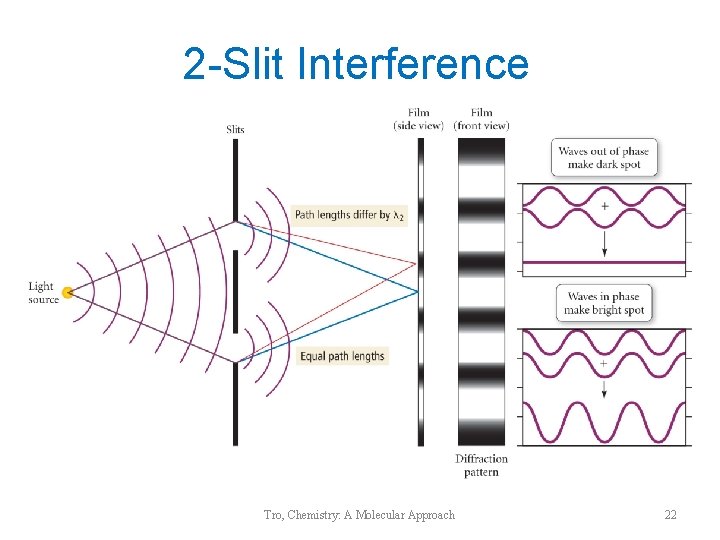
Interference: When Waves Interact

Diffraction

2 -Slit Interference Tro, Chemistry: A Molecular Approach 22

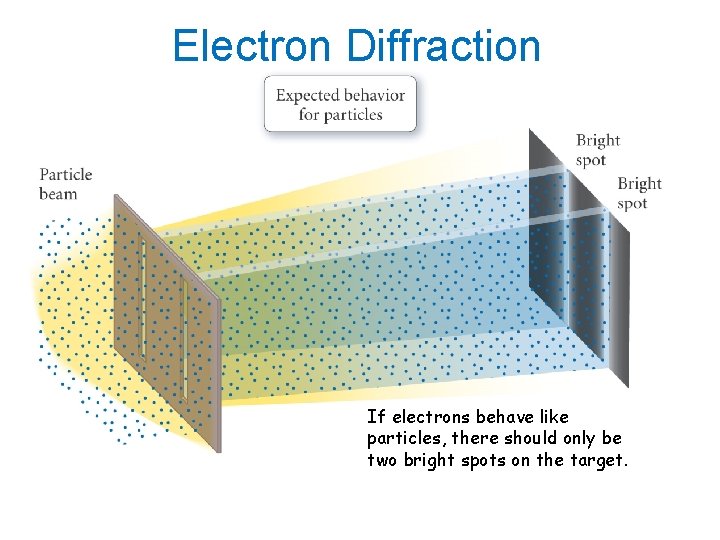
Electron Diffraction If electrons behave like particles, there should only be two bright spots on the target.

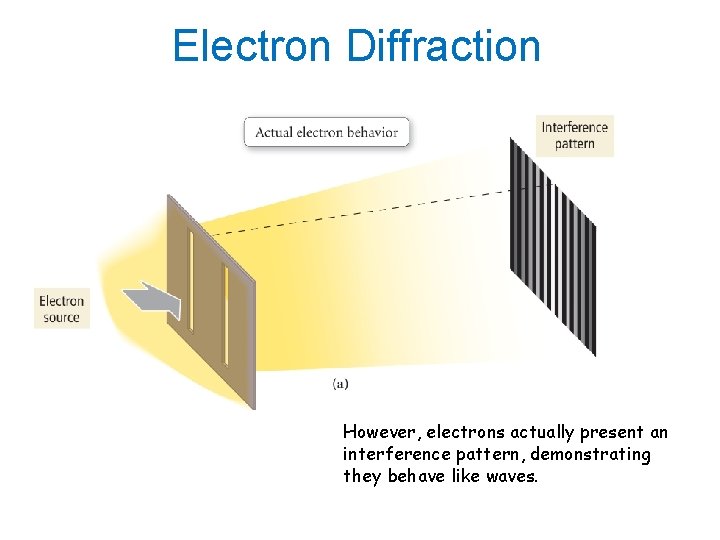
Electron Diffraction However, electrons actually present an interference pattern, demonstrating they behave like waves.

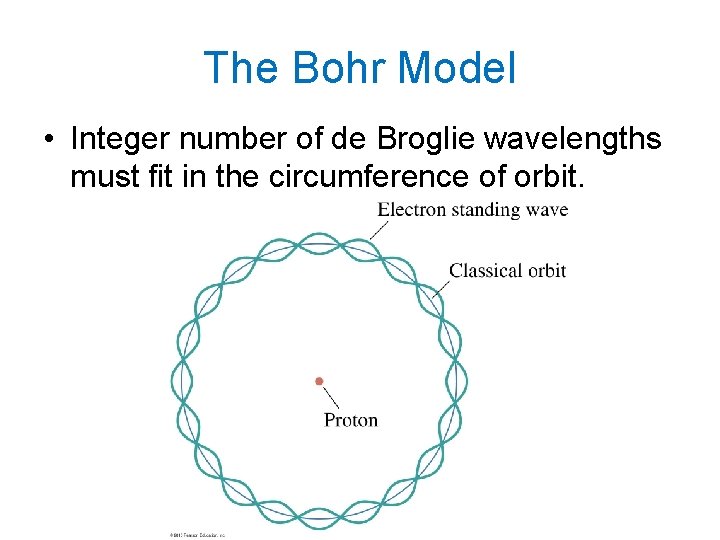
The Bohr Model • Integer number of de Broglie wavelengths must fit in the circumference of orbit.

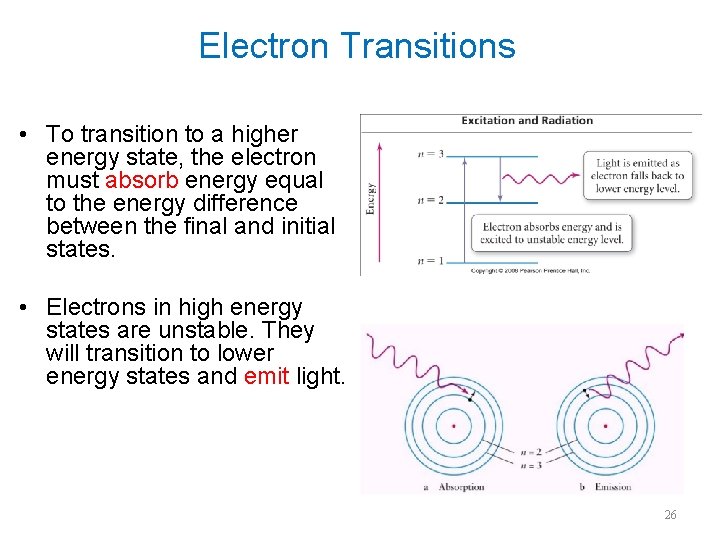
Electron Transitions • To transition to a higher energy state, the electron must absorb energy equal to the energy difference between the final and initial states. • Electrons in high energy states are unstable. They will transition to lower energy states and emit light. 26

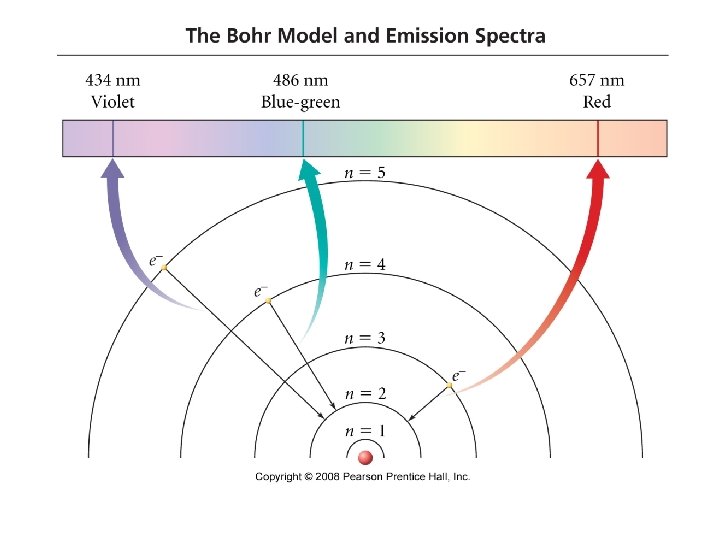
Principal Energy Levels in Hydrogen The wavelengths of lines in the emission spectrum of hydrogen can be predicted by calculating the difference in energy between any two states.

Bohr Model of H Atoms

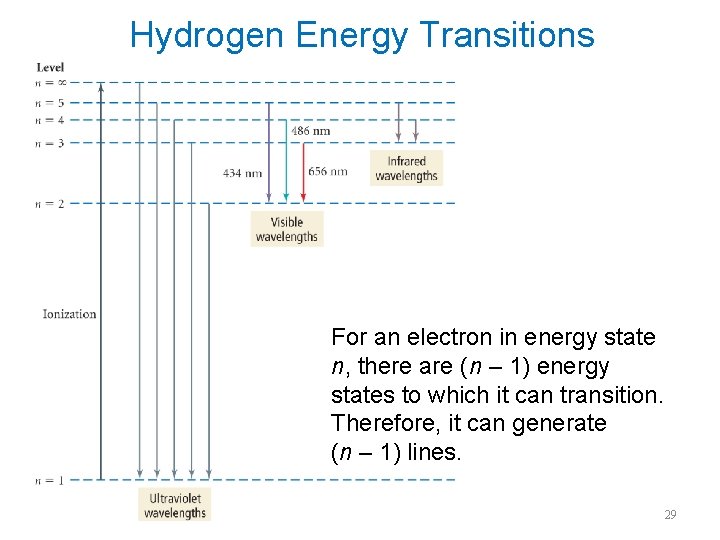
Hydrogen Energy Transitions For an electron in energy state n, there are (n – 1) energy states to which it can transition. Therefore, it can generate (n – 1) lines. 29

Chemical Fingerprints • Every atom, ion, and molecule has a unique spectral “fingerprint. ” • We can identify the chemicals in gas by their fingerprints in the spectrum. • With additional physics, we can figure out abundances of the chemicals, and much more.

Other spectroscopy • Many spectroscopic techniques rely on these electronic transitions used with different sources of light. • Energy can also be absorbed and emitted in other “modes” including vibration and rotation, leading to other types of spectra. OH

Uncertainty Principle • Heisenberg stated that the product of the uncertainties in both the position and speed of a particle was inversely proportional to its mass. – x = position, Δx = uncertainty in position – v = velocity, Δv = uncertainty in velocity – m = mass • The more accurately you know the position of a small particle, like an electron, the less you know about its speed. – and vice-versa

Wave Function, y • Calculations show that the size, shape and orientation in space of an orbital are determined by three integer terms in the wave function. – added to quantize the energy of the electron • These integers are called quantum numbers. – – principal quantum number, n angular momentum quantum number, l magnetic quantum number, ml spin quantum number, ms

Principal Quantum Number, n • characterizes the energy of the electron in a particular orbital – corresponds to Bohr’s energy level • n can be any integer. • The larger the value of n, the more energy the orbital has. • Energies are defined as being negative. – An electron would have E = 0 when it just escapes the atom. • The larger the value of n, the larger the orbital. • As n gets larger, the amount of energy between orbitals gets smaller. En = -2. 18 x 10 -18 J 1 n 2 for an electron in H

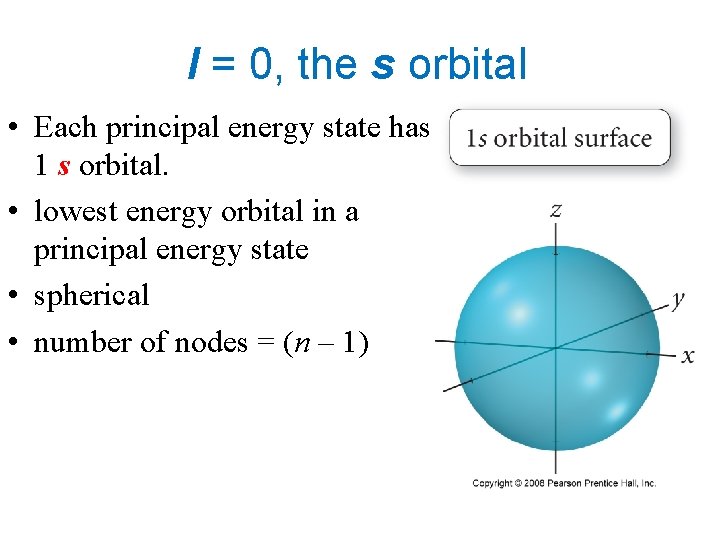
l = 0, the s orbital • Each principal energy state has 1 s orbital. • lowest energy orbital in a principal energy state • spherical • number of nodes = (n – 1)

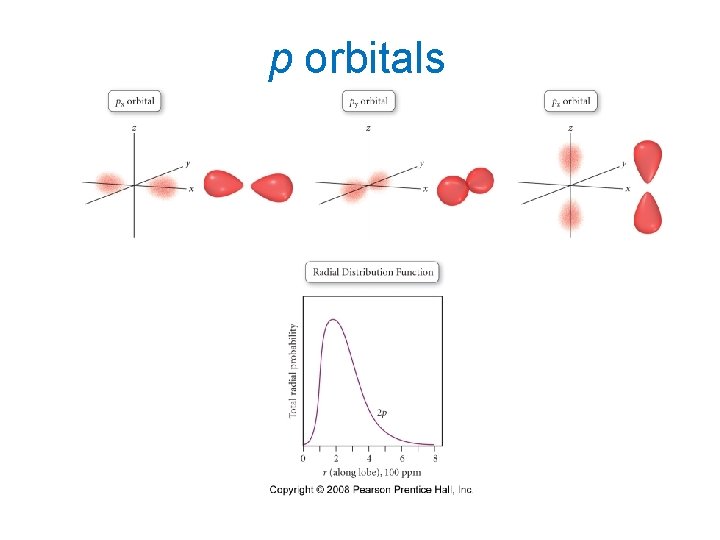
p orbitals

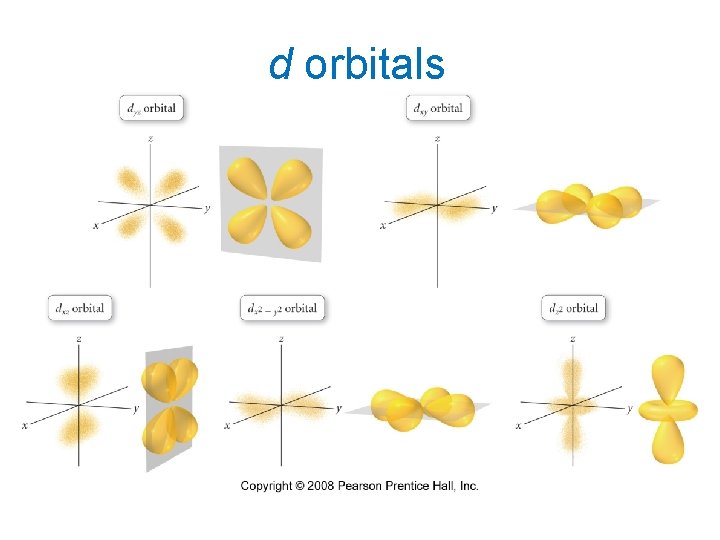
d orbitals

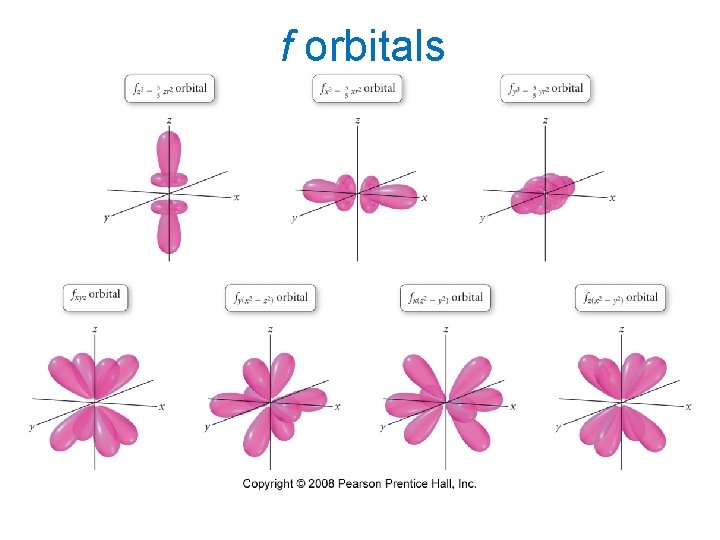
f orbitals