Spectral Decomposition of Open Channel Flow Xavier Litrico

Spectral Decomposition of Open Channel Flow Xavier Litrico (Cemagref, UMR G-EAU, Montpellier) with Vincent Fromion (INRA MIG, Jouy-en-Josas)

Motivation • • • Agriculture = 70% of fresh water world consumption Irrigated agriculture = 17% of agricultural area, 40% of food production Water for agriculture • • • Large operational losses: 20% to 70% Strong incentives to limit them: save water in summer and users requiring a better service Towards automatic management • • • Improve water resource management Improve service to user Facilitate irrigation canal operational management

Objective • • • Canal dynamics are complex Represented by nonlinear PDE: Saint-Venant equations Linear approach leads to effective results But no existing classification for canal dynamics Objective: understand the dynamics of linearized Saint. Venant equations • • Frequency domain approach Poles Spectral decomposition From horizontal frictionless canal to uniform and non uniform cases

Different views of irrigation canals

Outline • • Introduction Modeling of open channel flow • • • Illustrations • • • Spectral decomposition Time domain response Horizontal frictionless case Uniform flow case Non uniform flow case Analysis of Preissmann discretization scheme A link between Riemann invariants and frequency domain approaches Conclusion

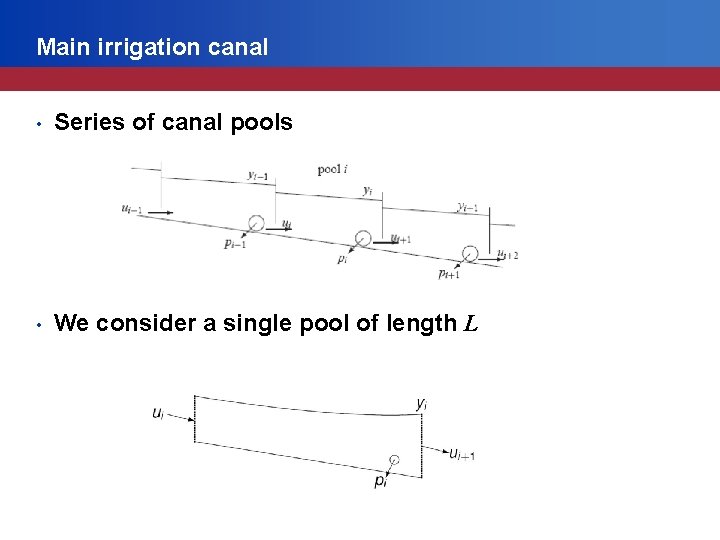
Main irrigation canal • Series of canal pools • We consider a single pool of length L

Modeling of open-channel flow Saint-Venant equations • • Mass conservation • Momentum conservation Friction slope: • Initial condition • Boundary conditions

Linearized Saint-Venant equations • Linearized around (non uniform) steady flow

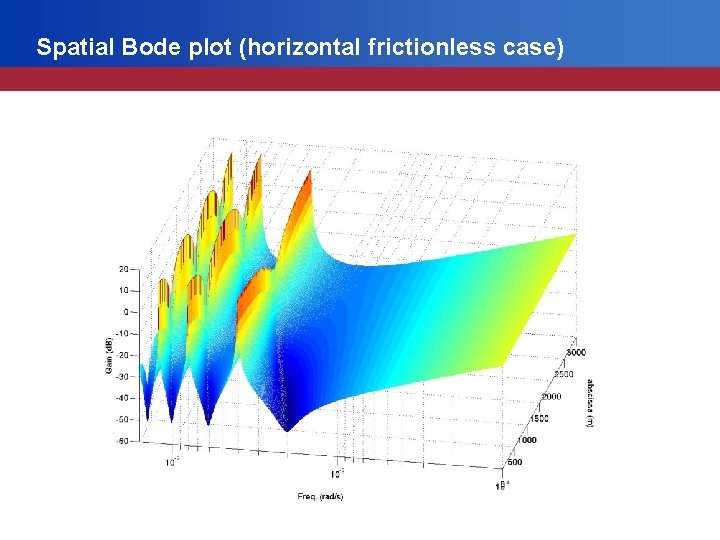
Frequency response • Laplace transform leads to a distributed transfer matrix: • Poles pk in the horizontal frictionless case

Spatial Bode plot (horizontal frictionless case)

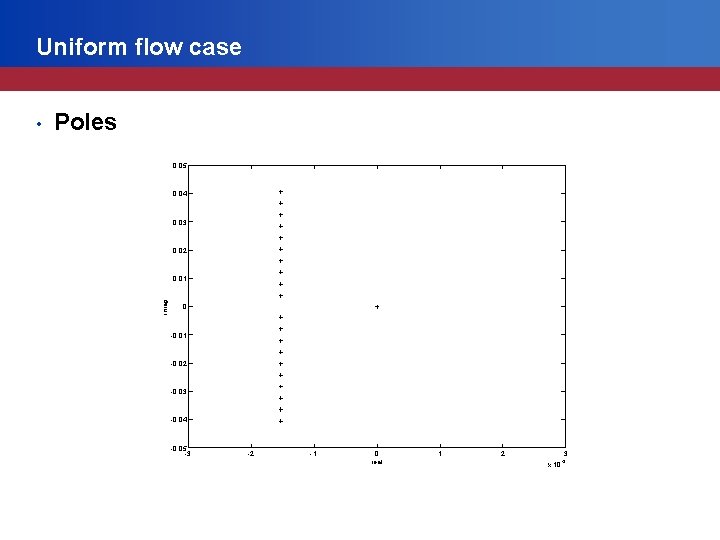
Uniform flow case Poles 0. 05 0. 04 0. 03 0. 02 0. 01 imag • 0 -0. 01 -0. 02 -0. 03 -0. 04 -0. 05 -3 -2 -1 0 real 1 2 3 x 10 -3

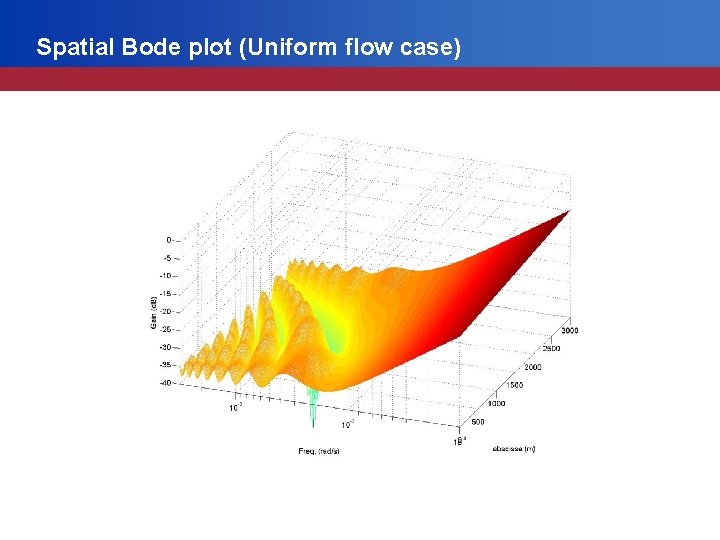
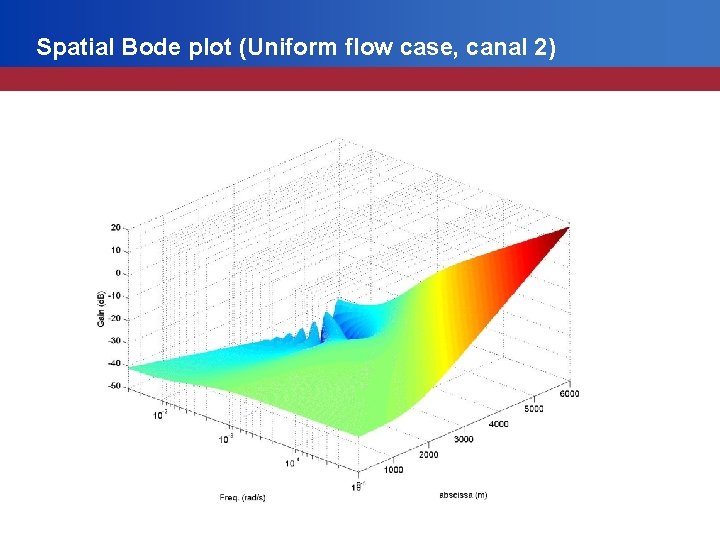
Spatial Bode plot (Uniform flow case)

Non uniform flow case • Compute the distributed transfer function using an efficient numerical procedure (Litrico & Fromion, J. of Hydraulic Engineering 2004) • • Compute the poles using this numerical method Conclusion: non uniform flow is qualitatively similar to uniform flow Question: can we decompose the system along the poles? Answer: Yes!

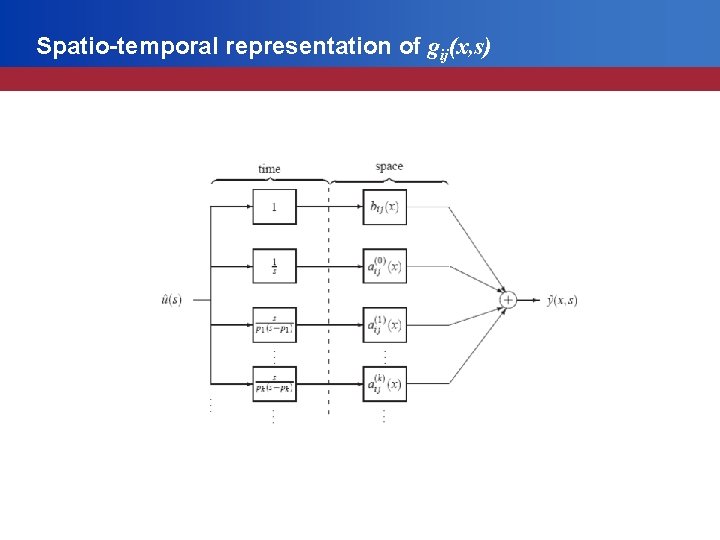
Main result: spectral decomposition • The elements gij(x, s) of the distributed transfer matrix G(x, s) can be decomposed as follows: aij(k)(x) is the residue of gij(x, s) at the pole pk

Spatio-temporal representation of gij(x, s)

Sketch of proof Define Apply the Cauchy residues theorem to on a series of nested contours CN gives

Implications • • • SV transfer matrix belongs to the Callier-Desoer class of transfer functions Nyquist criterion provides a necessary and sufficient condition for input-output stability Link with exponential stability using dissipativity approach (see Litrico & Fromion, Automatica, 2009, in press)

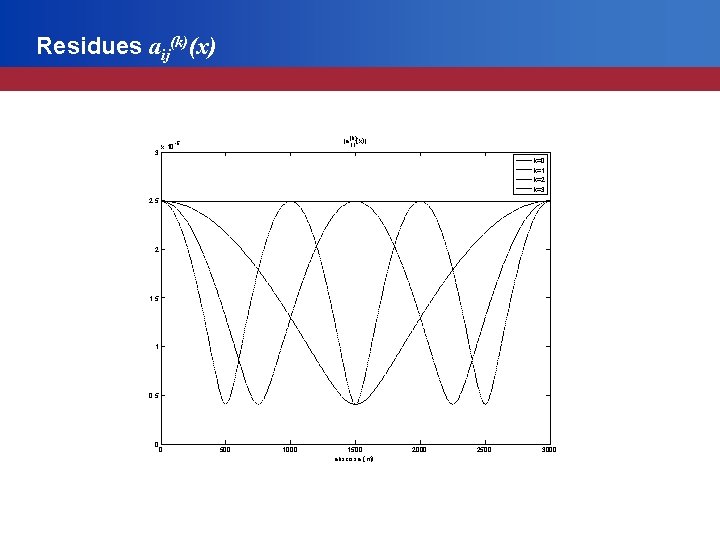
Horizontal frictionless case Residues aij(k)(x)

Residues aij(k)(x) 3 x 10 |a (k)(x)| -5 11 k=0 k=1 k=2 k=3 2. 5 2 1. 5 1 0. 5 0 0 500 1000 1500 abscissa (m) 2000 2500 3000

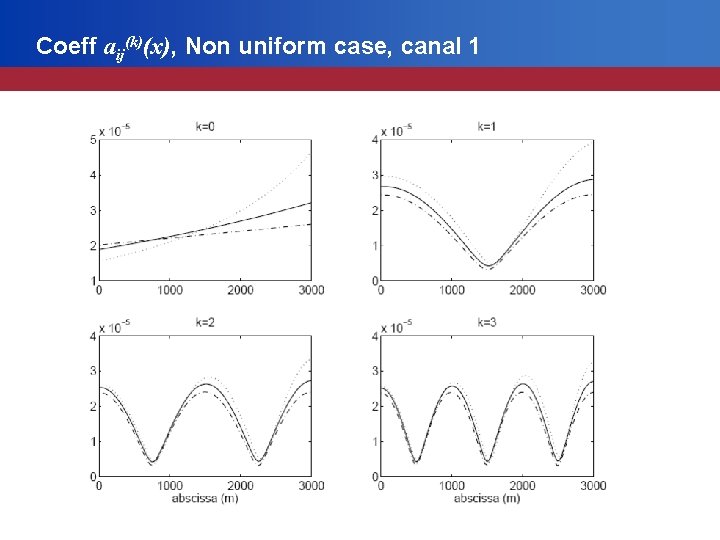
Coeff aij(k)(x), Non uniform case, canal 1

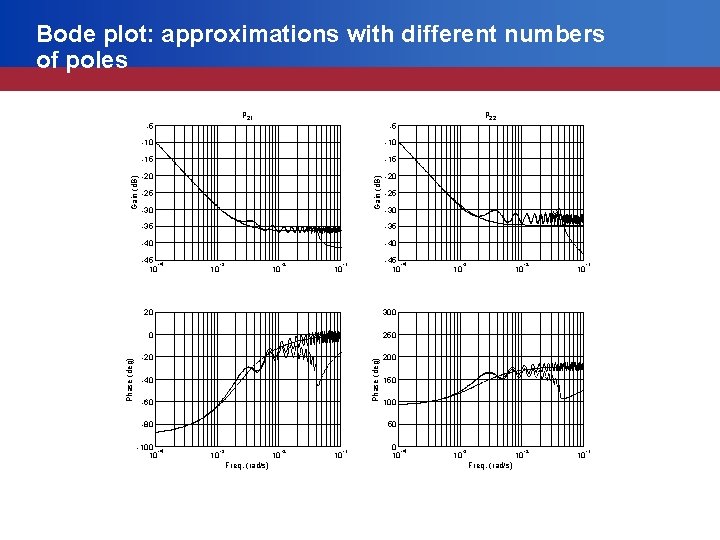
Bode plot: approximations with different numbers of poles -10 -15 -20 Gain (d. B) -10 -25 -30 -35 -40 -45 -4 10 Phase (deg) p 22 -5 10 -3 10 -2 10 -45 -4 10 -1 20 300 0 250 -20 200 Phase (deg) Gain (d. B) p 21 -5 -40 -60 -80 -100 -4 10 10 -3 10 -2 10 -1 150 100 50 10 -3 10 Freq. (rad/s) -2 10 -1 0 -4 10 10 -3 10 Freq. (rad/s) -2 10 -1

Time response • Rational approximations • Unit step response

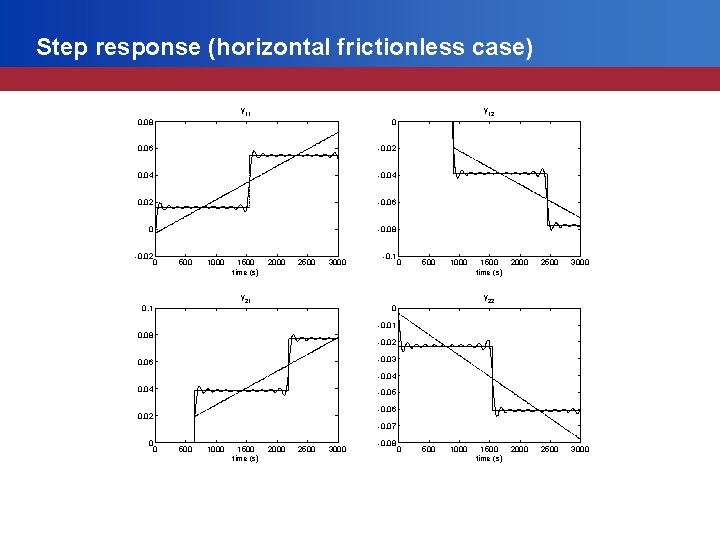
Step response (horizontal frictionless case) y 11 y 12 0. 08 0 0. 06 -0. 02 0. 04 -0. 04 0. 02 -0. 06 0 -0. 08 -0. 02 0 500 1000 1500 time (s) 2000 2500 3000 -0. 1 0 500 1000 y 21 1500 time (s) 2000 2500 3000 y 22 0. 1 0 -0. 01 0. 08 -0. 02 -0. 03 0. 06 -0. 04 -0. 05 -0. 06 0. 02 -0. 07 0 0 500 1000 1500 time (s) 2000 2500 3000 -0. 08 0 500 1000 1500 time (s)

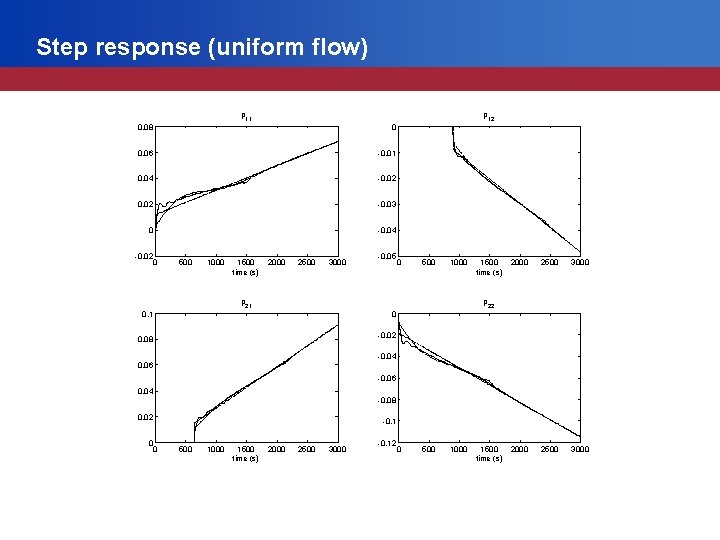
Step response (uniform flow) p 11 p 12 0. 08 0 0. 06 -0. 01 0. 04 -0. 02 -0. 03 0 -0. 04 -0. 02 0 500 1000 1500 time (s) 2000 2500 3000 -0. 05 0 500 1000 p 21 1500 time (s) 2000 2500 3000 p 22 0. 1 0 -0. 02 0. 08 -0. 04 0. 06 -0. 06 0. 04 -0. 08 0. 02 0 0 -0. 1 500 1000 1500 time (s) 2000 2500 3000 -0. 12 0 500 1000 1500 time (s)

Spatial Bode plot (Uniform flow case, canal 2)

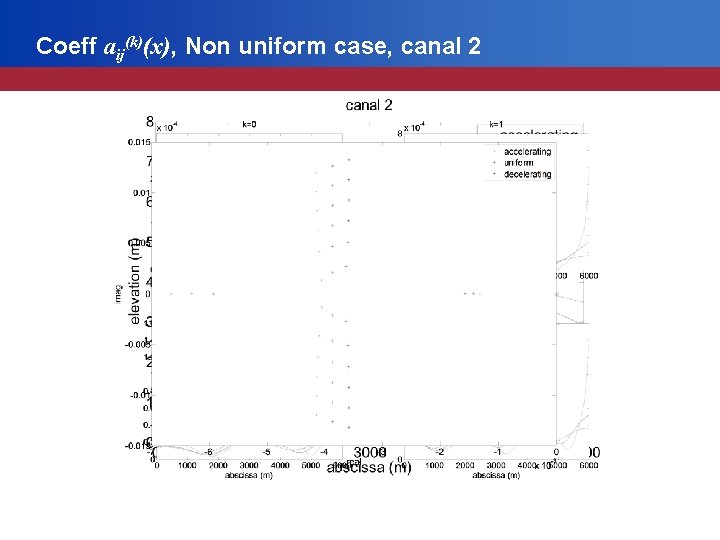
Coeff aij(k)(x), Non uniform case, canal 2

Applications • • • Preissmann scheme = Classical numerical scheme used to solve the equations We study the scheme on the linearized equations We relate the discretized poles to the continuous ones • • Poles location as a function of Dt , Dx and q Root locus with a downstream controller

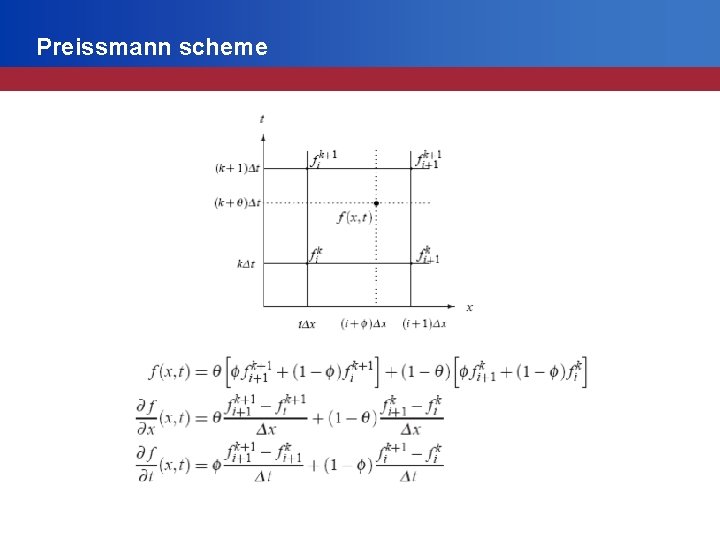
Preissmann scheme

Study of the discretized system • The linearized SV equations discretized with this scheme give Assuming non trivial solution is , the condition for the existence of a with

Study of the discretized system (cont’d) or with And finally This equation is formally identical to the one obtained in the continuous time case!!! One may show that the poles can be computed in two steps: • first compute the continuous time poles obtained due to the spatial discretization • then compute the discrete time poles

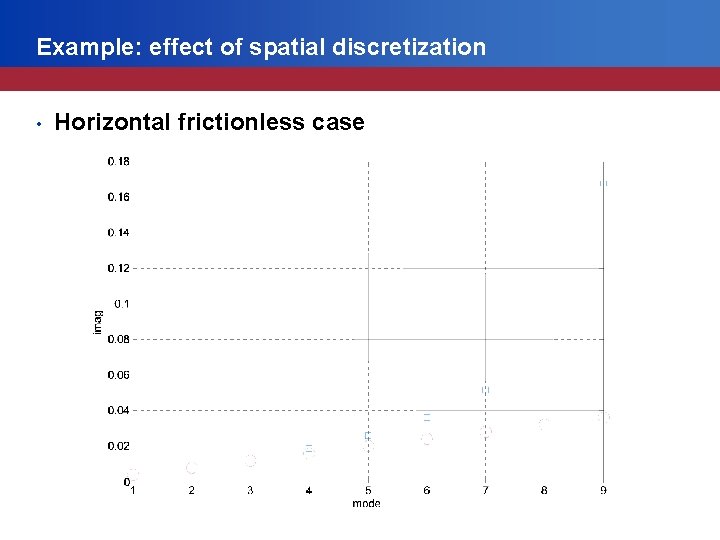
Example: effect of spatial discretization • Horizontal frictionless case

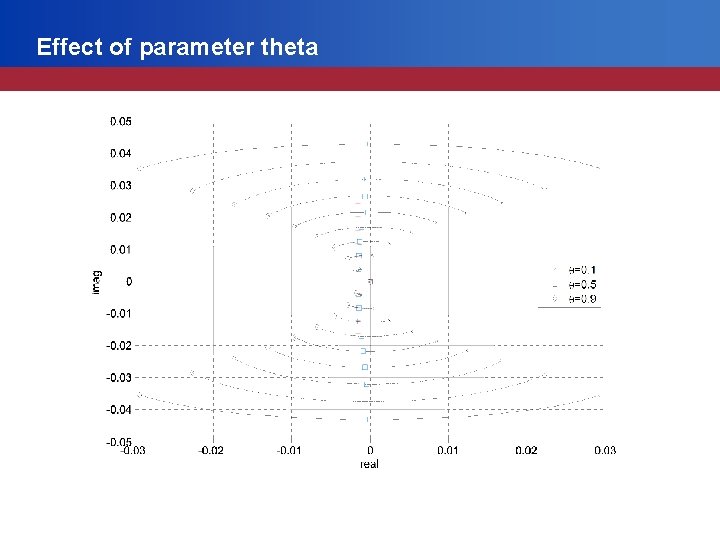
Effect of parameter theta

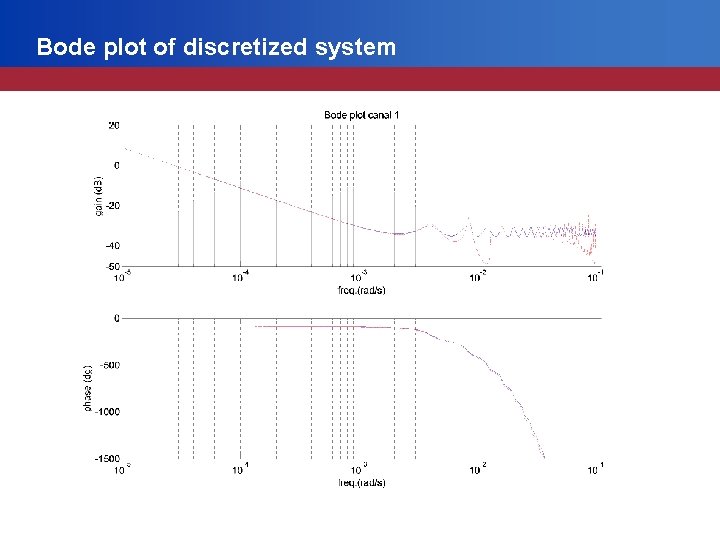
Bode plot of discretized system

A link between frequency domain and Riemann invariants methods • For horizontal frictionless canals, Riemann invariants and frequency domain methods lead to the same result: • • Open-channel flow can be represented by a delay system How to extend this to the case of nonzero slope and friction? For nonzero slope and friction, Riemann coordinates are no longer invariants! But frequency domain methods enable to diagonalize the system…

Riemann invariants (horizontal frictionless case) SV equations Diagonalize matrix A Laplace transform This is a delay system!

Uniform flow case (with slope and friction) SV equations Laplace transform + diagonalize matrix A-1(s. I+B): New variables:

Uniform flow case (cont’d) Solution in the Laplace domain: « generalized » delay system We have: and with

Solution in the time domain Time evolution of generalized characteristics Change of variables with

Solution in the time domain (cont’d) Change of variables Inverse Laplace transform

Solution in the time domain Inverse transform (time)

Application: motion planning We want to find the controls steering the system from 0 to a desired state in a given time Tr. The evolution equation leads to:

Feedback control Controller or with System Closed-loop system Sufficient stability condition

Control of SV oscillating modes: root locus

Control of SV oscillating modes

Conclusion • • Analysis of linearized Saint-Venant equations Poles and spectral decomposition • • Analytical results in horizontal frictionless and uniform cases Numerical method in non uniform cases Rational models Complete characterization of the flow dynamics Analysis of Preissmann discretization scheme Generalized characteristics (using Bessel functions) More details and applications in the book « Modeling and control of hydrosystems » , Springer, to appear in 2009.