Specification and Implementation of Abstract Data Types cs

Specification and Implementation of Abstract Data Types cs 784(Prasad) L 34 ADT 1

Data Abstraction • Clients – Interested in WHAT services a module provides, not HOW they are carried out. So, ignore details irrelevant to the overall behavior, for clarity. • Implementors – Reserve the right to change the code, to improve performance. So, ensure that clients do not make unwarranted assumptions. cs 784(Prasad) L 34 ADT 2

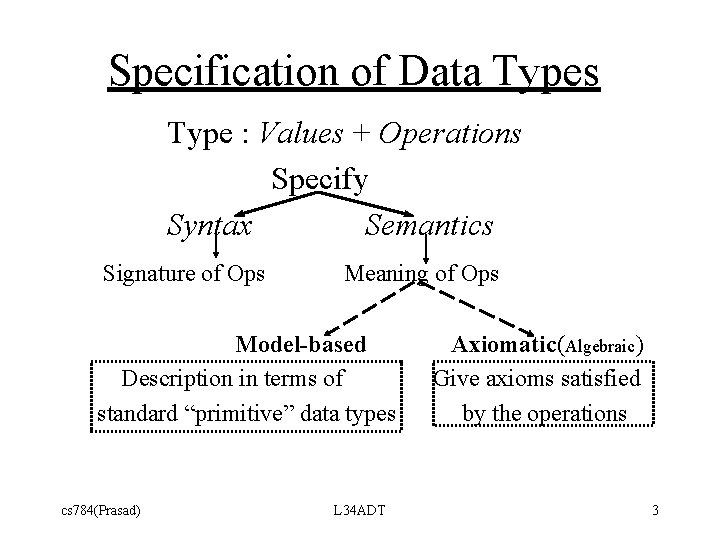
Specification of Data Types Type : Values + Operations Specify Syntax Semantics Signature of Ops Meaning of Ops Model-based Description in terms of standard “primitive” data types cs 784(Prasad) L 34 ADT Axiomatic(Algebraic) Give axioms satisfied by the operations 3

Syntax of LISP S-expr • operations: nil, cons, car, cdr, null • signatures: nil: cons: car: cdr: null: S-expr * S-expr -> S-expr -> boolean for every atom a: a: cs 784(Prasad) S-expr L 34 ADT 4

• Signature tells us how to form complex terms from primitive operations. • Legal nil null(cons(nil, nil)) cons(car(nil), nil) • Illegal nil(cons) null(null) cons(nil) cs 784(Prasad) L 34 ADT 5

Semantics of +: What to expect? + : N x N -> N 1 + 2 = 3 zero + succ(zero)) x + 0 2 * (3 + 4) = = succ(zero)) = x 2*7 = 14 = 6+8 x * ( y + z) = y * x + x * z cs 784(Prasad) L 34 ADT 6

Semantics of S-Expr : What to expect? null(nil) = true car(cons(nil, nil)) = nil null(cdr(cons(nil, nil)))) = false • for all E, F in S-Expr car(cons(E, F)) = E null(cons(E, F)) = false cs 784(Prasad) L 34 ADT 7

Formal Spec. of ADTs Characteristics of an “Adequate” Specification – Completeness (No “undefinedness”) – Consistency/Soundness (No conflicting definitions) • Minimality GOAL: Learn to write sound and complete algebraic(axiomatic) specifications of ADTs cs 784(Prasad) L 34 ADT 8

Classification of Operations • Observers – generate a value outside the type • E. g. , null in ADT S-expr • Constructors – required for representing values in the type • E. g. , nil, cons, atoms a in ADT S-expr • Non-constructors – remaining operations • E. g. , car, cdr in ADT S-expr cs 784(Prasad) L 34 ADT 9

S-Expr in LISP a : nil : cons : car : cdr : null : S-Expr S-Expr x S-Expr -> boolean Observers : Constructors : Non-constructors : cs 784(Prasad) L 34 ADT null a, nil, cons car, cdr 10

Algebraic Spec • Write axioms (equations) that characterize the meaning of all the operations. • Describe the meaning of the observers and the non-constructors on all possible constructor patterns. • Note the use of typed variables to abbreviate the definition. (“Finite Spec. ”) cs 784(Prasad) L 34 ADT 11

• for all S, T in S-expr cdr(nil) = ? error? cdr(cons(S, T)) = T car(nil) = ? error? car(cons(S, T)) = S null(nil) = true null(cons(S, T)) = false cdr(a) = ? error? car(a) = ? error? null(a) = false • Omitting the equation for “nil” implies that implementations that differ in the interpretation of “nil” are all equally acceptable cs 784(Prasad) L 34 ADT 12

S-Exprs • car(a) • cons(a, nil) • car(cons(a, nil)) • a = • cons( car(cons(a, nil)), cdr(cons(a, a)) ) • cons( a , a ) = cs 784(Prasad) L 34 ADT 13

Motivation for Classification : Minimality • If car and cdr are also regarded as constructors (as they generate values in the type), then the spec. must consider other cases to guarantee completeness (or provide sufficient justification for their omission). • for all S in S-expr: null(car(S)) =. . . null(cdr(S)) =. . . cs 784(Prasad) L 34 ADT 14

ADT Table (symbol table/directory) empty : Table update : Key x Info x Table -> Table look. Up: Key x Table -> Info look. Up(K, empty) = error look. Up(K, update(Ki, I, T)) = if K = Ki then I else look. Up(K, T) (“last update overrides the others”) cs 784(Prasad) L 34 ADT 15

Tables Table • • empty update(5, “abc”, empty) update(10, “xyz”, update(5, “abc”, empty)) update(5, “xyz”, update(5, “abc”, empty)) (Search ) • • lookup (5, update(5, “xyz”, update(5, “abc”, empty)) ) lookup (5, update(5, “xyz”, empty) ) “xyz” cs 784(Prasad) L 34 ADT 16

Implementations – Array-based – Linear List - based – Tree - based • Binary Search Trees, AVL Trees, B-Trees etc – Hash Table - based • These exhibit a common Table behavior, but differ in performance aspects (search time). • Correctness of a program is assured even when the implementation is changed as long as the spec is satisfied. cs 784(Prasad) L 34 ADT 17

(cont’d) • Accounts for various other differences (Data Invariants) in implementation such as – Eliminating duplicates. – Retaining only the final binding. – Maintaining the records sorted on the key. – Maintaining the records sorted in terms of the frequency of use (a la caching). cs 784(Prasad) L 34 ADT 18

A-list in LISP a : A nil : cons : car : cdr : null : A-list A x A-list -> A A-list -> boolean • Observers : • Constructors : • Non-constructors : cs 784(Prasad) L 34 ADT null, car nil, cons cdr 19

• for all L in A-list cdr(cons(a, L)) = L car(cons(a, L)) = a null(nil) = true null(cons(a, L)) = false • Consciously silent about nil-list. cs 784(Prasad) L 34 ADT 20

Natural Numbers zero : succ : add : iszero N N -> N N x N -> N : N -> boolean observers : iszero constructors : zero, succ non-constructors : add Each number has a unique representation in terms of its constructors. cs 784(Prasad) L 34 ADT 21

for all I, J in N add(I, J) = ? add(zero, I) = I add(succ(J), I) = succ(add(J, I)) iszero(I) = ? iszero(zero) = true iszero(succ(I)) = false cs 784(Prasad) L 34 ADT 22

(cont’d) add(succ(zero)), succ(zero)) = succ(succ(zero))) � The first rule eliminates add from an expression, while the second rule simplifies the first argument to add. � Associativity, commutativity, and identity properties of add can be deduced from this definition through purely mechanical means. cs 784(Prasad) L 34 ADT 23

A-list Revisted a : A nil list append null : : A-list A -> A-list x A-list -> boolean • values – nil, list(a), append(nil, list(a)), . . . cs 784(Prasad) L 34 ADT 24

Algebraic Spec • constructors – nil, list, append • observer isnull(nil) = true isnull(list(a)) = false isnull(append(L 1, L 2)) = isnull(L 1) / isnull(L 2) cs 784(Prasad) L 34 ADT 25

• Problem : Same value has multiple representation in terms of constructors. • Solution : Add axioms for constructors. – Identity Rule append(L, nil) = L append(nil, L) = L – Associativity Rule append(L 1, L 2), L 3) = append(L 1, append(L 2, L 3)) cs 784(Prasad) L 34 ADT 26

Intuitive understanding of constructors • The constructor patterns correspond to distinct memory/data patterns required to store/represent values in the type. • The constructor axioms can be viewed operationally as rewrite rules to simplify constructor patterns. Specifically, constructor axioms correspond to computations necessary for equality checking and aid in defining a normal form. • Cf. cs 784(Prasad) == vs equal in Java L 34 ADT 27

Writing ADT Specs • Idea: Specify “sufficient” axioms such that syntactically distinct terms (patterns) that denote the same value can be proven so. – Completeness • Define non-constructors and observers on all possible constructor patterns – Consistency • Check for conflicting reductions • Note: A term essentially records the detailed history of construction of the value. cs 784(Prasad) L 34 ADT 28

General Strategy for ADT Specs • Syntax – Specify signatures and classify operations. • Constructors – Write axioms to ensure that two constructor terms that represent the same value can be proven so. • E. g. , identity, associativity, commutativity rules. cs 784(Prasad) L 34 ADT 29

• Non-constructors – Provide axioms to collapse a non-constructor term into a term involving only constructors. • Observers – Define the meaning of an observer on all constructor terms, checking for consistency. Implementation of a type An interpretation of the operations of the ADT that satisfies all the axioms. cs 784(Prasad) L 34 ADT 30

Declarative Specification • Let *: N x N -> N denote integer multiplication. Equation: Solution: n*n = n n = 0 / n = 1. • Let f: N x N -> N denote a binary integer function. Equation: 0 f 0 = 0 Solution: f = “multiplication” / f = “addition” / f = “subtraction” /. . . cs 784(Prasad) L 34 ADT 31

delete : Set • for all n, m in N, s in Set delete(n, empty) = empty delete(n, insert(m, s)) = if (n=m) then delete(n, s) (invalid: s) else insert(m, delete(n, s)) delete(5, insert(5, empty)) ) [] == empty {} [5] =/= insert(5, empty) cs 784(Prasad) L 34 ADT [5, 5] {5, 5} 32

delete : List • Previous axioms capture “remove all occurrences” semantics. • For “remove last occurrence” semantics: for all n, m in N, s in List delete(n, empty) = empty delete(n, insert(m, s)) = if (n=m) then s else insert(m, delete(n, s)) delete(5, insert(5, empty)) ) == insert(5, empty) cs 784(Prasad) L 34 ADT [5, 5] [5] 33

delete : List • Previous axioms capture “remove all / last occurrences” semantics. • For “remove first occurrence” semantics: for all n, m in N, s in List delete(n, empty) = empty delete(n, insert(m, s)) = if (n=m) and not (n in s) then s else insert(m, delete(n, s)) delete(1, insert(2, insert(1, insert(5, empty)))) ) == insert(1, insert(2, insert(5, empty))) cs 784(Prasad) L 34 ADT [5, 1, 2, 1] [5, 2, 1] 34

size: List vs Set • size(insert(m, l)) = 1 + size(l) – E. g. , size([2, 2, 2]) = 1 + size([2, 2]) • size(insert(m, s)) = if (m in s) then size(s) else 1 + size(s) – E. g. , size({2, 2, 2}) = size ({2}) cs 784(Prasad) = size({2, 2}) = 1 L 34 ADT 35

Model-based vs Algebraic • A model-based specification of a type satisfies the corresponding axiomatic specification. Hence, algebraic spec. is “more abstract” than the model-based spec. • Algebraic spec captures the least commondenominator (behavior) of all possible implementations. cs 784(Prasad) L 34 ADT 36

Axiomatization: Algebraic Structures • A set G with operation * forms a group if • Closure: a, b e G implies a*b e G. • Associativity: a, b, c e G implies a*(b *c) = (a*b)*c. • Identity: There exists i e G such that i*a = a*i = a for all a e G. • Inverses: For every a e G there exists an element ~a e G such that a * ~a = ~a * a = i. • Examples: • (Integers, +), but not (N, +) • (Reals - {0}, *), but not (Integers, *) • (Permutation functions, Function composition) cs 784(Prasad) L 34 ADT 37

Example car( cons( X, Y) ) = X cdr( cons (X, Y) ) = Y (define (cons x y) (lambda (m) (cond ((eq? m ’first) x) (eq? m ’second) y) ) )) ; “closure” (define (car z) (z ’first)) (define (cdr z) (z ’second)) cs 784(Prasad) L 34 ADT 38

Applications of ADT spec • Least common denominator of all possible implementations. – Focus on the essential behavior. • An implementation is a refinement of ADT spec. – IMPL. = Behavior SPEC + Rep “impurities” – To prove equivalence of two implementations, show that they satisfy the same spec. – In the context of OOP, a class implements an ADT, and the spec. is a class invariant. cs 784(Prasad) L 34 ADT 39

(Cont’d) • Indirectly, ADT spec. gives us the ability to vary or substitute an implementation. – E. g. , In the context of interpreter/compiler, a function definition and the corresponding calls (ADT Func. Values) together must achieve a fixed goal. However, there is freedom in the precise apportioning of workload between the two separate tasks: • How to represent the function? • How to carry out the call? cs 784(Prasad) L 34 ADT 40

(Cont’d) • ADT spec. are absolutely necessary to automate formal reasoning about programs. Theorem provers such as Boyer-Moore prover (NQTHM), LARCH, PVS, HOL, etc routinely use such axiomatization of types. • Provides a theory of equivalence of values that enables design of a suitable canonical form. • Identity • Associativity • Commutativity cs 784(Prasad) -> delete -> remove parenthesis -> sort L 34 ADT 41

Spec vs Impl The reason to focus on the behavioral aspects, ignoring efficiency details initially, is that the notion of a “best implementation” requires application specific issues and trade-offs. In other words, the distribution of work among the various operations is based on a chosen representation, which in turn, is dictated by the pragmatics of an application. However, in each potential implementation, there is always some operations that will be efficient while others will pay the price for this comfort. cs 784(Prasad) L 34 ADT 42

Ordered Integer Lists null nil hd tl ins order : oil -> boolean : oil -> int : oil -> oil : int x oil -> oil : int_list -> oil Constructors: Non-constructors: Observers: cs 784(Prasad) nil, ins tl, order null, hd L 34 ADT 43

• Problem: – syntactically different, but semantically equivalent constructor terms ins(2, ins(5, nil)) = ins(5, ins(2, nil)) = ins(2, nil) – hd should return the smallest element. • It is not the case that for all I in int, L in oil, hd(ins(I, L)) = I. • This holds iff I is the minimum in ins(I, L). – Similarly for tl. cs 784(Prasad) L 34 ADT 44

Axioms for Constructors • Idempotence – for all ordered integer lists L; for all I in int ins(I, L)) = ins(I, L) • Commutativity – for all ordered integer lists L; for all I, J in int ins(I, ins(J, L)) = ins(J, ins(I, L)) Completeness : Any permutation can be generated by exchanging adjacent elements. cs 784(Prasad) L 34 ADT 45

Axioms for Non-constructors tl(nil) = error tl(ins(I, L)) = ? tl(ins(I, nil)) = nil tl(ins(I, ins(J, L))) = I < J => ins( J, tl(ins(I, L)) ) I > J => ins( I, tl(ins(J, L)) ) I = J => tl( ins( I, L ) ) (cf. constructor axioms for duplicate elimination) order(nil) = nil order(cons(I, L)) = ins(I, order(L)) cs 784(Prasad) L 34 ADT 46

Axioms for Observers hd(nil) = error hd(ins(I, nil)) = I hd(ins(I, ins(J, L))) = I < J => hd( ins(I, L) ) I > J => hd( ins(J, L) ) I = J => hd( ins(I, L) ) null(nil) null(ins(I, L)) cs 784(Prasad) = = L 34 ADT true false 47

Scheme Implementation (define null? ) (define nil ’()) (define ins cons) (define (hd ol) *min* ) (define (tl ol) *list sans min* ) (define (order lis) *sorted list* ) cs 784(Prasad) L 34 ADT 48

Possible Implementations • Representation Choice 1: – List of integers with duplicates • ins is cons but hd and tl require linear-time search • Representation Choice 2: – Sorted list of integers without duplicates • ins requires search but hd and tl can be made more efficient • Representation Choice 3: – Balanced-tree : Heap cs 784(Prasad) L 34 ADT 49