Specific Heat Relations of Ideal Gases A special

Specific Heat Relations of Ideal Gases A special relationship between cp and cv for ideal gases can be obtained by differentiating the relation h = u +RT, which yields: Replacing dh by cp d. T and du by cv d. T and dividing the resulting expression by d. T, we obtain When the specific heats are given on a molar basis, R in the above equation should be replaced by the universal gas constant Ru : At this point, we introduce another ideal-gas property called the specific heat ratio k, defined as:

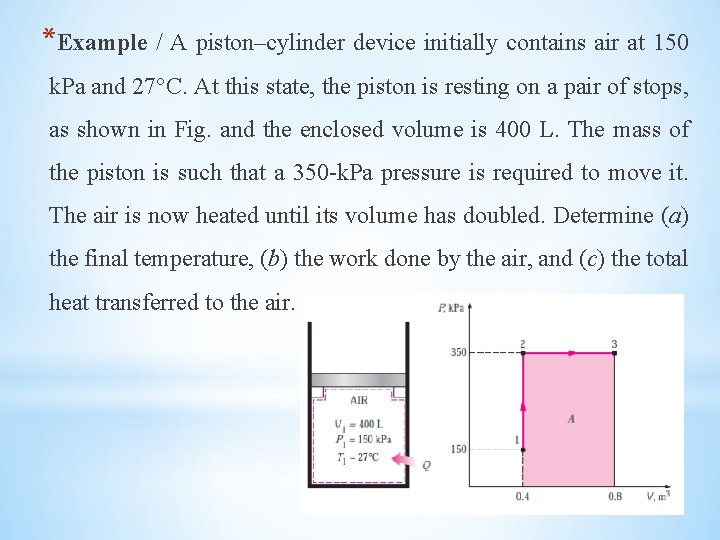
*Example / A piston–cylinder device initially contains air at 150 k. Pa and 27°C. At this state, the piston is resting on a pair of stops, as shown in Fig. and the enclosed volume is 400 L. The mass of the piston is such that a 350 -k. Pa pressure is required to move it. The air is now heated until its volume has doubled. Determine (a) the final temperature, (b) the work done by the air, and (c) the total heat transferred to the air.

*INTERNAL ENERGY, ENTHALPY, AND SPECIFIC HEATS OF SOLIDS AND LIQUIDS A substance whose specific volume (or density) is constant is called an incompressible substance. The specific volumes of solids and liquids essentially remain constant during a process. Therefore, liquids and solids can be approximated as incompressible substances without sacrificing much in accuracy The constant-volume and constant-pressure specific heats are identical for incompressible substances. Therefore, for solids and liquids, the subscripts on cp and cv can be dropped, and both specific heats can be represented by a single symbol c. That is,

*Internal Energy Changes Like those of ideal gases, the specific heats of incompressible substances depend on temperature only. Thus, the partial differentials in the defining equation of cv can be replaced by ordinary differentials, which yield * The change in internal energy between states 1 and 2 is then obtained by integration: * For small temperature intervals, a c value at the average temperature can be used and treated as a constant, yielding

Enthalpy Changes Using the definition of enthalpy h= u + Pv and noting that v= constant, the differential form of the enthalpy change of incompressible substances can be determined by differentiation to be: *Integrating,