Specialist Mathematics Slope fields direction fields Geometric interpretation

Specialist Mathematics Slope fields (direction fields).

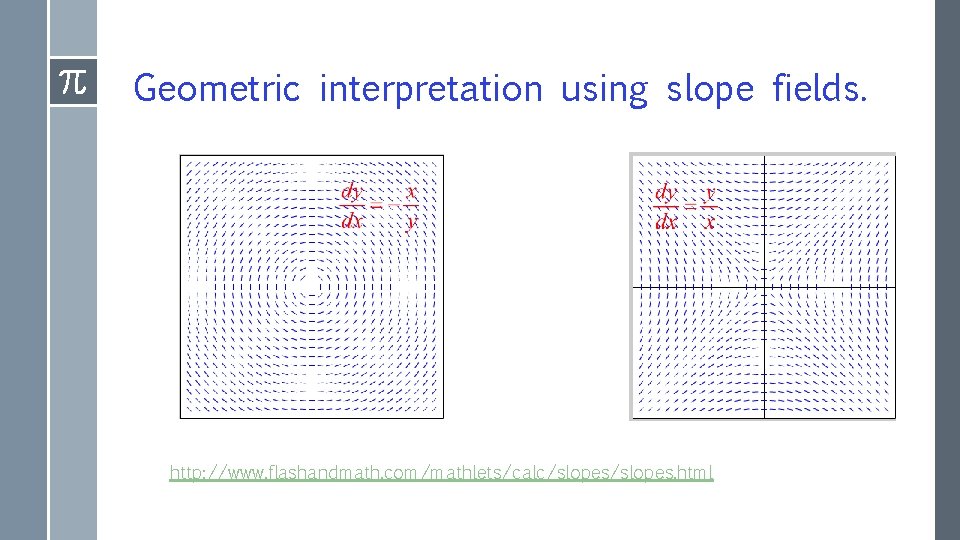
Geometric interpretation using slope fields. http: //www. flashandmath. com/mathlets/calc/slopes. html

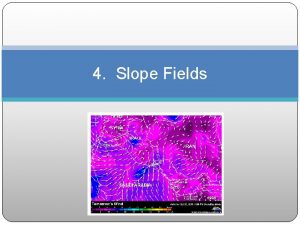
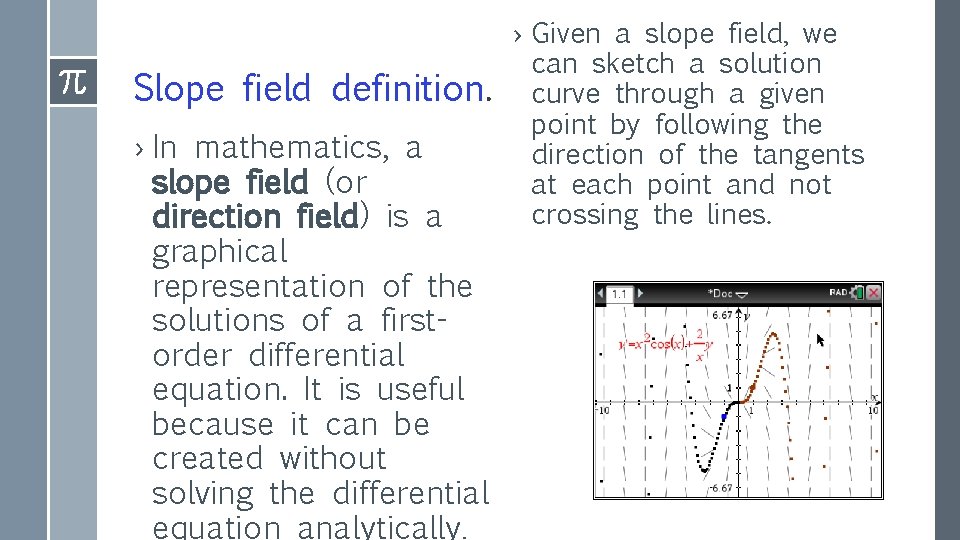
Slope field definition. › In mathematics, a slope field (or direction field) is a graphical representation of the solutions of a firstorder differential equation. It is useful because it can be created without solving the differential equation analytically. › Given a slope field, we can sketch a solution curve through a given point by following the direction of the tangents at each point and not crossing the lines.

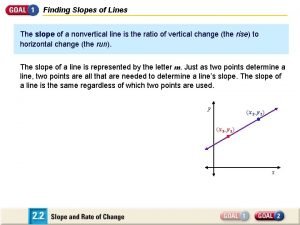
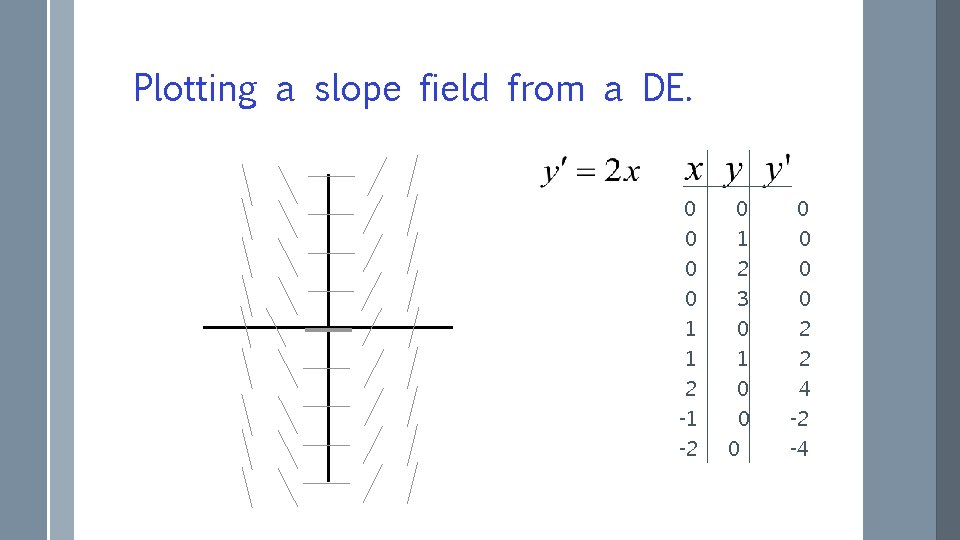
Slope Field or Direction Field A slope field or a direction field for the first order differentiable equation is a plot of line segments with slopes f(x, y) for a lattice of points (x, y) in the plane. To do so, we construct a table first, finding the slope for various pairs of coordinate points. For example, given y’=-2 xy, we can calculate the slope at the point where x =1 and y=-1 as y’=2 and plot a short line segment at this point.

Plotting a slope field from a DE. 0 0 1 2 0 0 1 1 2 -1 -2 3 0 1 0 0 2 2 4 -2 -4

Introduction to slope fields activity. Objective: Find graphically a particular solution of a given differential equation, and confirm it algebraically. Please refer to a handout.

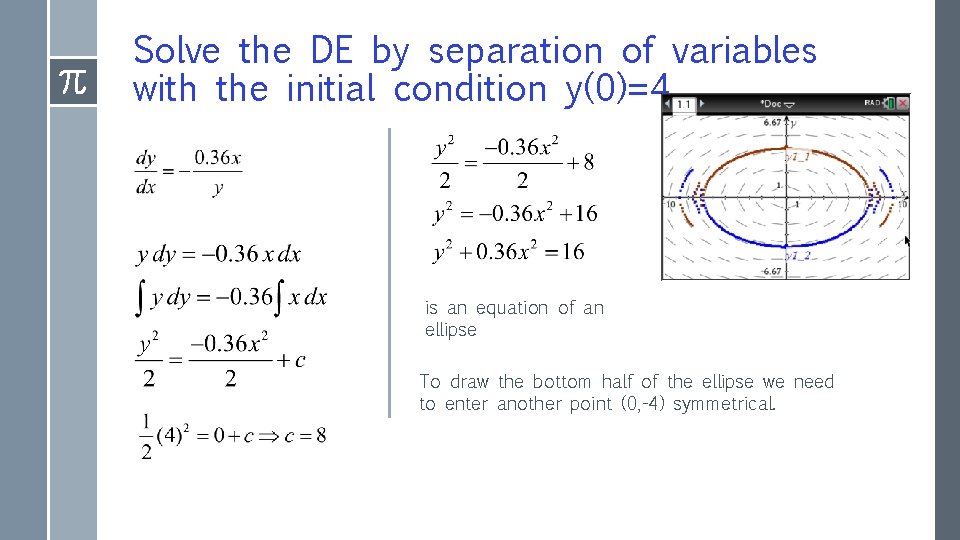
Solve the DE by separation of variables with the initial condition y(0)=4. is an equation of an ellipse To draw the bottom half of the ellipse we need to enter another point (0, -4) symmetrical.

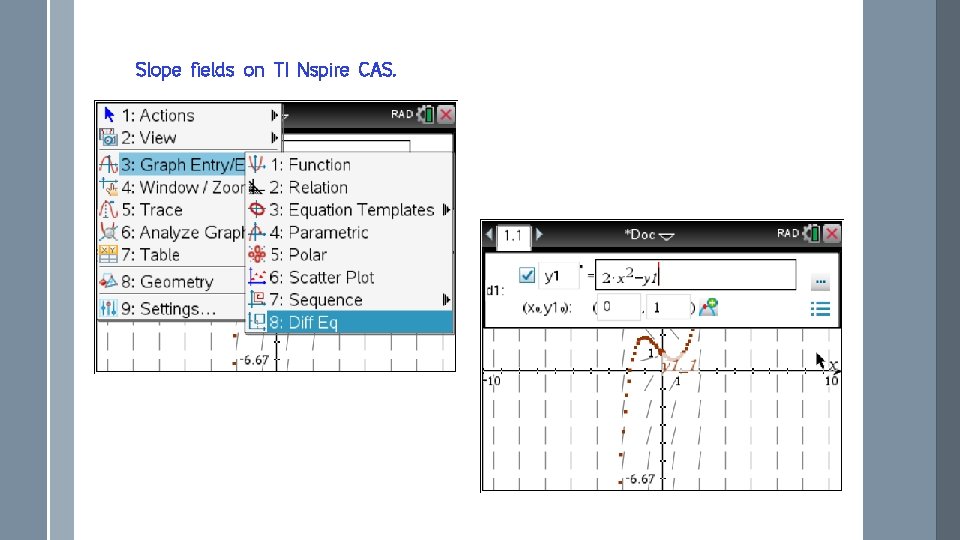
Slope fields on TI Nspire CAS.

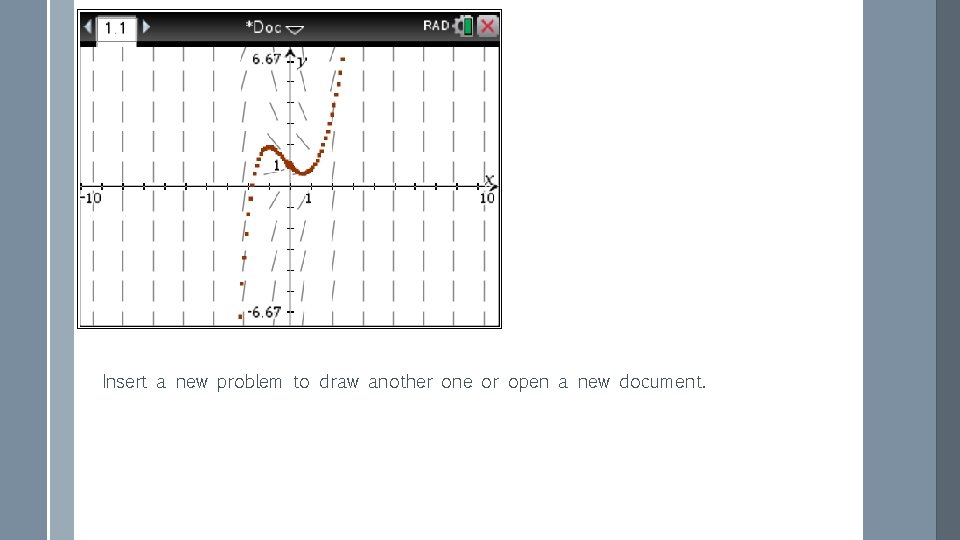
Insert a new problem to draw another one or open a new document.

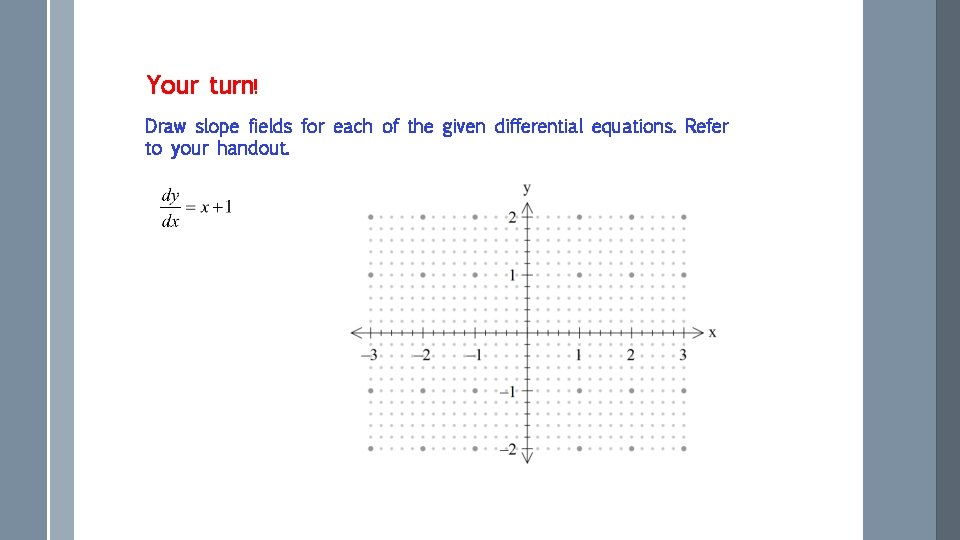
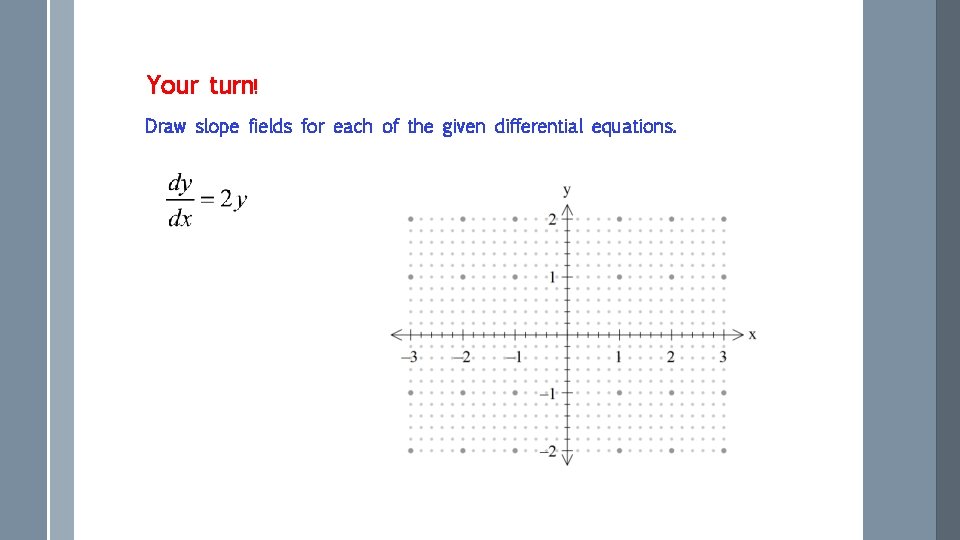
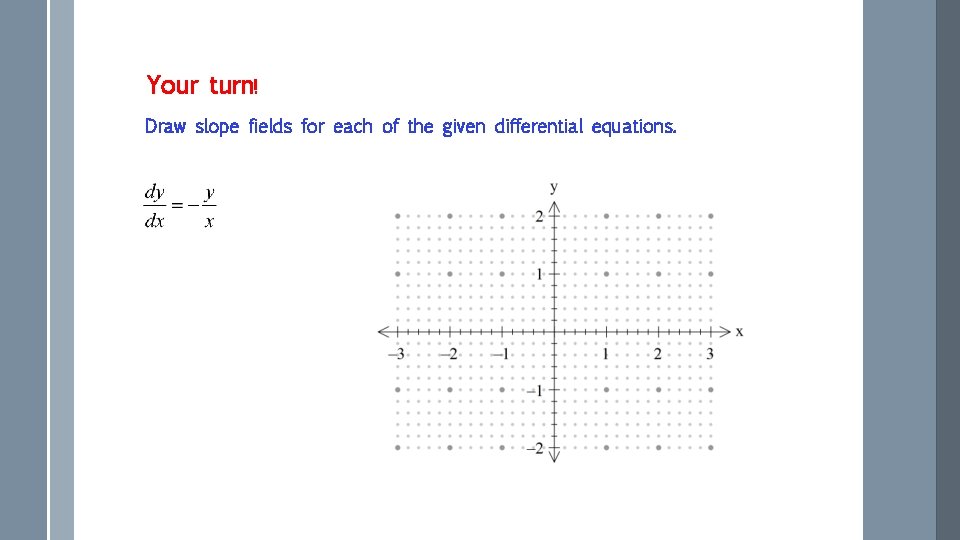
Your turn! Draw slope fields for each of the given differential equations. Refer to your handout.

Your turn! Draw slope fields for each of the given differential equations.

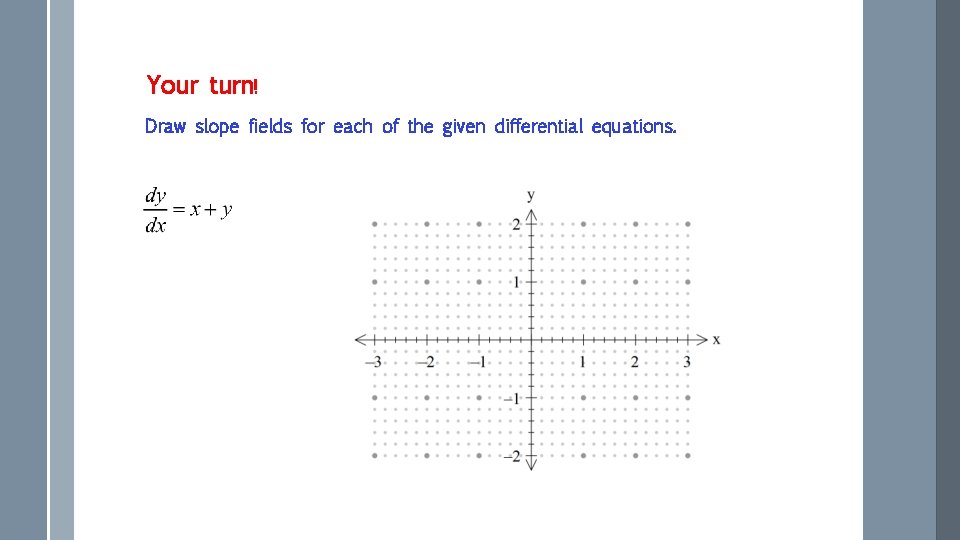
Your turn! Draw slope fields for each of the given differential equations.

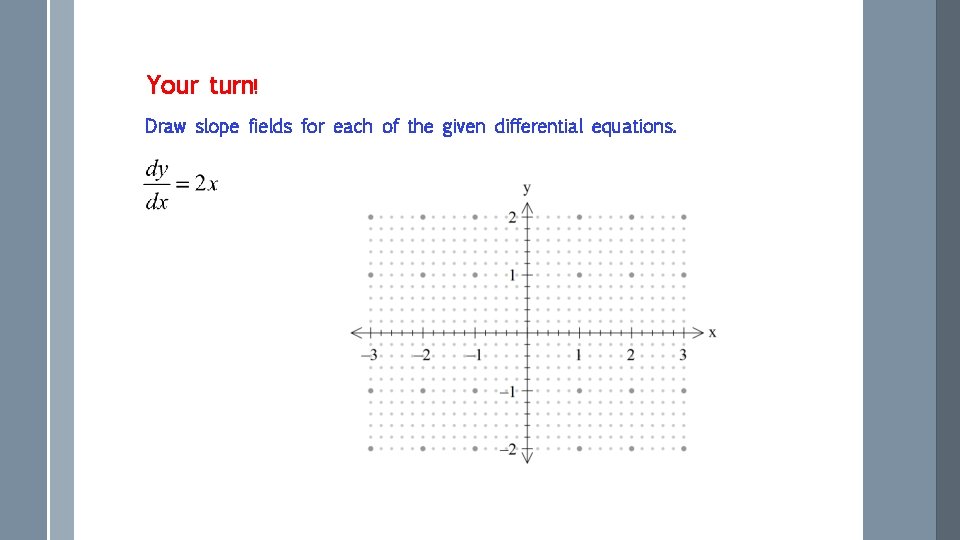
Your turn! Draw slope fields for each of the given differential equations.

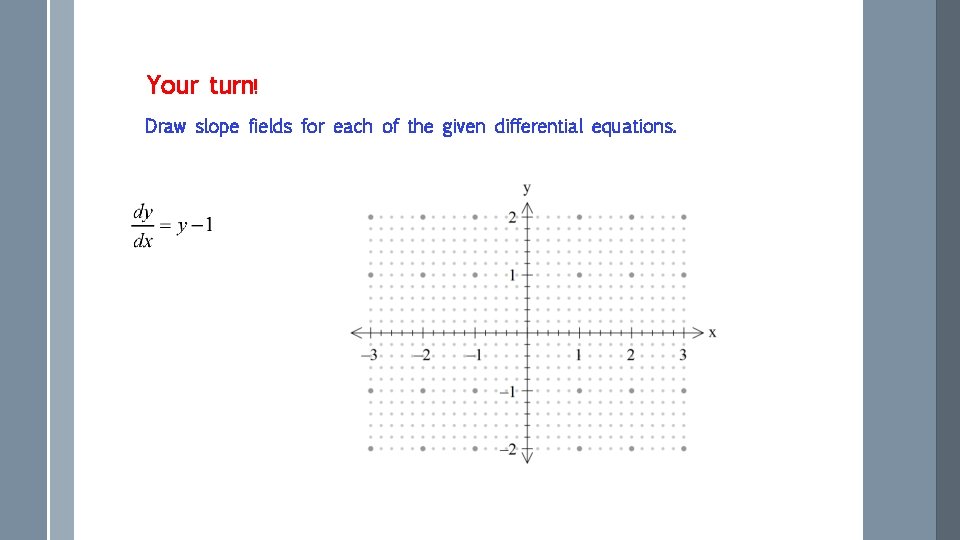
Your turn! Draw slope fields for each of the given differential equations.

Your turn! Draw slope fields for each of the given differential equations.

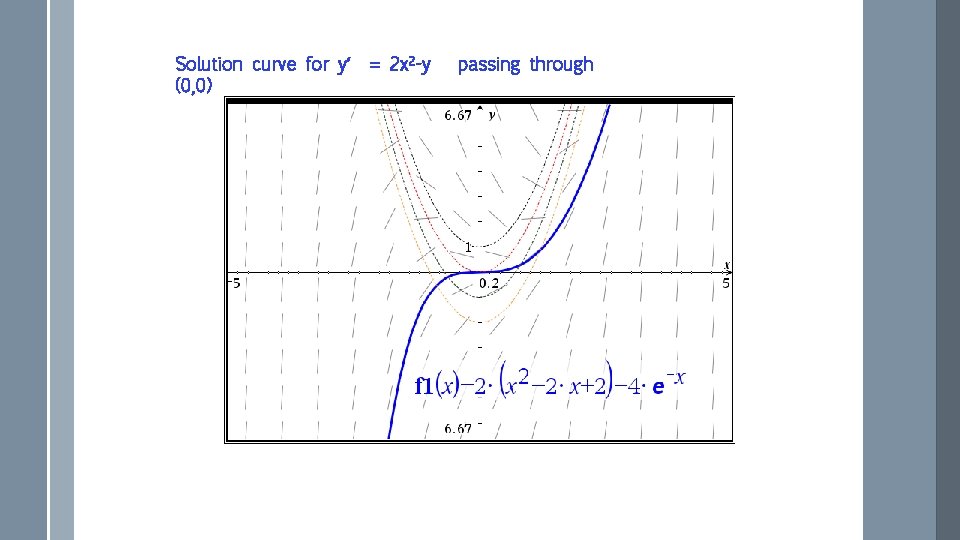
Direction field for y′ = 2 x 2 -y

Solution curve for y′ (0, 0) = 2 x 2 -y passing through

The goal is for students to be able to do the following with slope fields: 1. Sketch a slope field for a given differential equation. 2. Given a slope field, sketch a solution curve through a given point. 3. Match a slope field to a differential equation. 4. Match a slope field to a solution of a differential equation. 5. Draw conclusions about the solution curves by looking at the slope field.

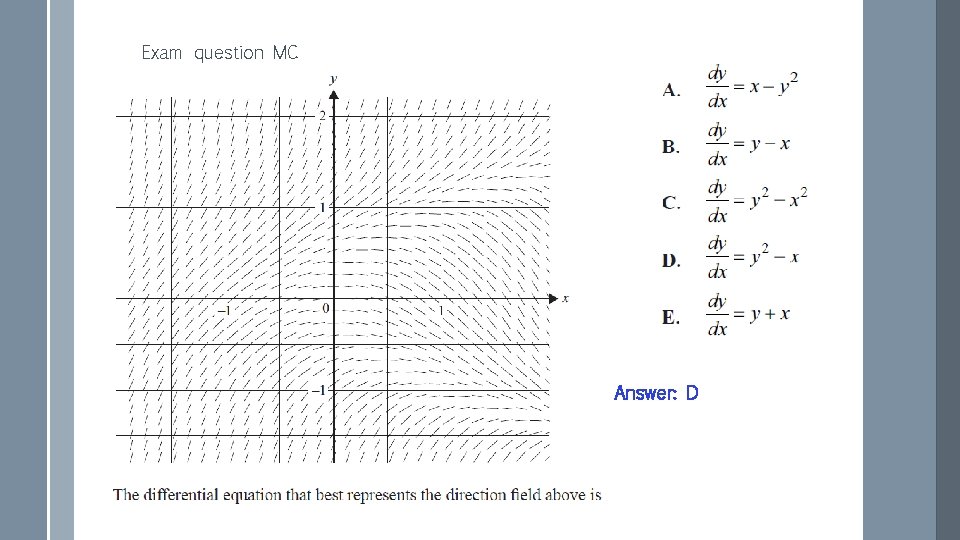
Exam question MC Answer: D

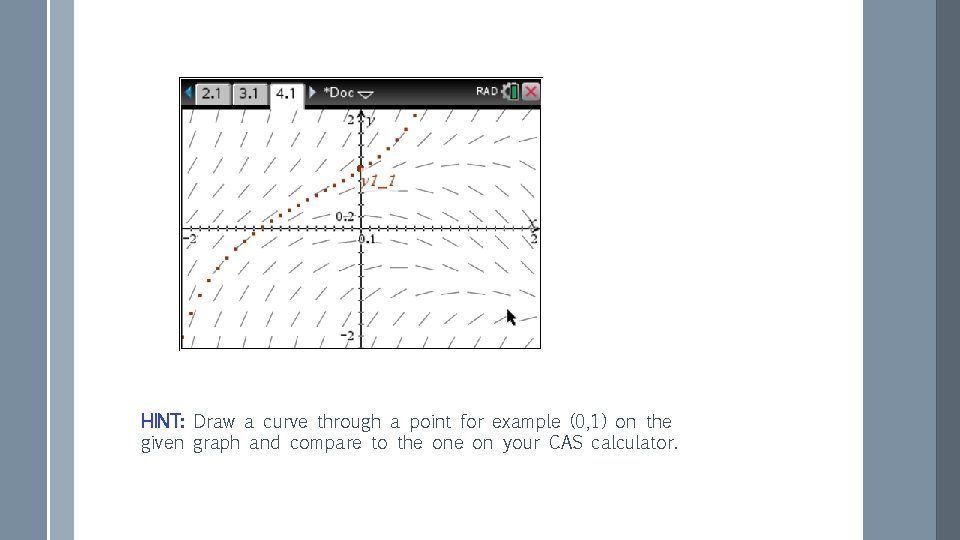
HINT: Draw a curve through a point for example (0, 1) on the given graph and compare to the on your CAS calculator.