Specialist Mathematics Eulers mehod Leonard Euler 1707 1783

Specialist Mathematics Euler’s mehod.

Leonard Euler (1707 – 1783) Leonhard Euler was a Swiss mathematician, physicist, astronomer, logician and engineer who made important and influential discoveries in many branches of mathematics like calculus and differential equations. Numerical solution of Euler’s method. using where h is a constant (step length) The above formulas are given in the formulae booklet so no need to memorise.

Euler’s Method. › Allows to find an approximate solution to a differential equation › Graphically we start at the point and find the gradient at this point. › This is done by finding a sequence of points which lie on the solution curve of the given differential equation with a boundary condition. › The step h is usually given in the question. The smaller the step, the more accurate the approximation. › We need to approximate numerically the value of yn at xn. As numerical calculations are quite time consuming when performed manually, the spreadsheet or computer programs are helpful to do all the calculations much quicker. › We move to the point by using the gradient calculated in step 1. › We repeat the process until we reach the point

Iterations, how it works: and so on…

Example 1: Use Euler’s method of numerical integration with a step size of 0. 1 to find y(1) if y’=y-x and y(0)=2. Identify the information given: Now multiply by h First calculate f(0, 2) Repeat the process with the point (x 1, y 1) Add to y 0 To obtain the point (x 2, y 2)

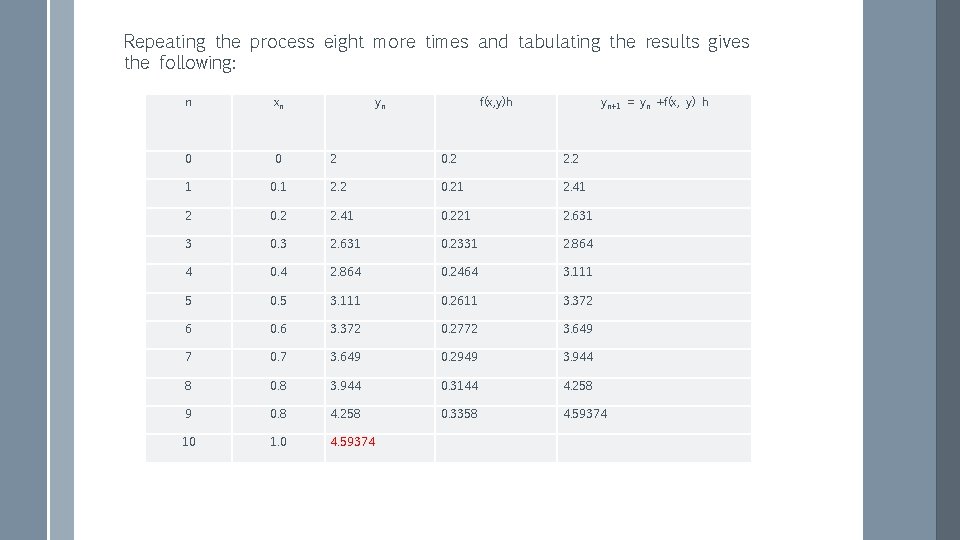
Repeating the process eight more times and tabulating the results gives the following: n xn 0 0 1 yn f(x, y)h yn+1 = yn +f(x, y) h 2 0. 2 2. 2 0. 1 2. 2 0. 21 2. 41 2 0. 2 2. 41 0. 221 2. 631 3 0. 3 2. 631 0. 2331 2. 864 4 0. 4 2. 864 0. 2464 3. 111 5 0. 5 3. 111 0. 2611 3. 372 6 0. 6 3. 372 0. 2772 3. 649 7 0. 7 3. 649 0. 2949 3. 944 8 0. 8 3. 944 0. 3144 4. 258 9 0. 8 4. 258 0. 3358 4. 59374 10 1. 0 4. 59374

How accurate is this result? When solving the above DE we obtain y=ex+x+1 So we have an underestimation here 4. 59374– 4. 71828 = 0. 12454 and the absolute percentage error of around 2. 64%, so not a bad approximation. This value can be also obtained using your TI Nspire CAS, sketch the slope field in the Diff Eq mode, enter the initial condition. Use Trace, Graph trace and left-right arrows to move along the curve in steps of 0. 1 (default) Edit parameters to change the step. Make sure Euler is

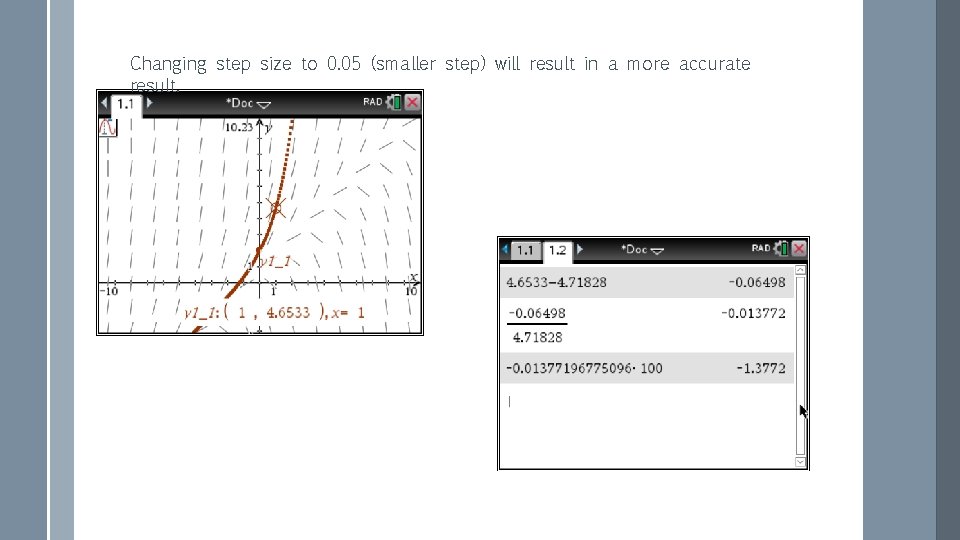
Changing step size to 0. 05 (smaller step) will result in a more accurate result.

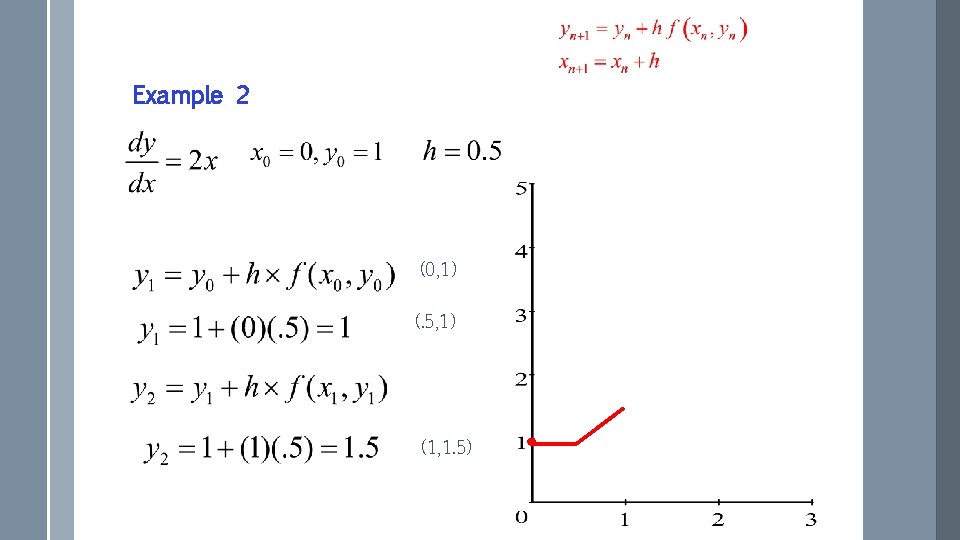
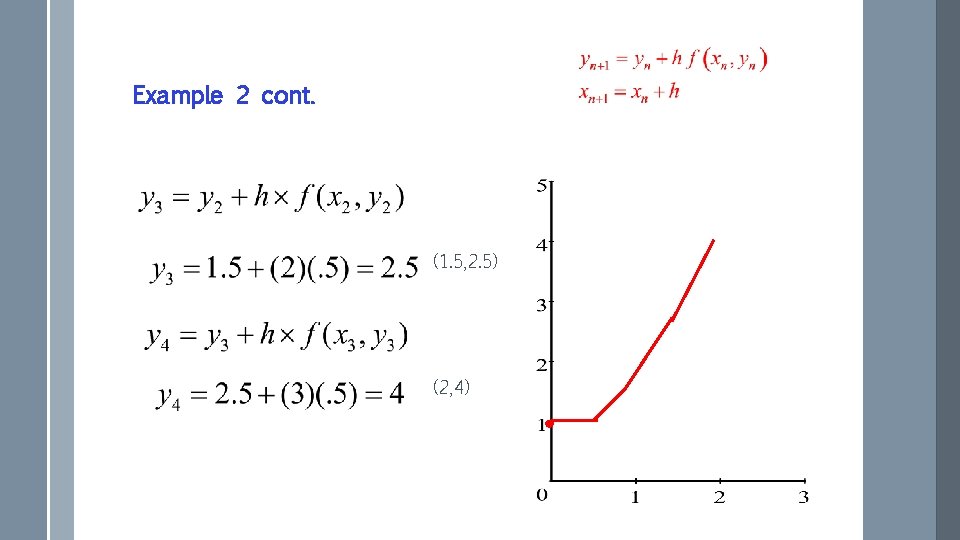
Example 2 (0, 1) (. 5, 1) (1, 1. 5)

Example 2 cont. (1. 5, 2. 5) (2, 4)

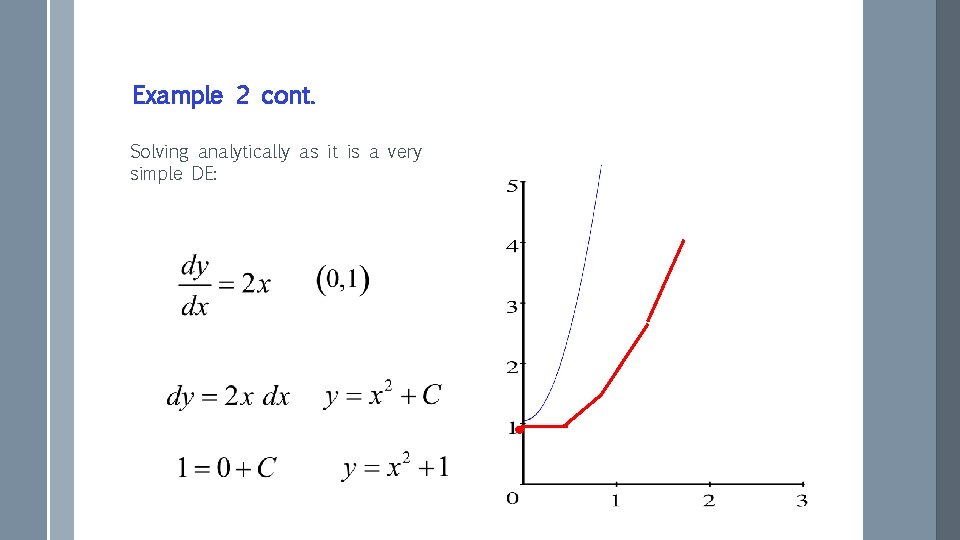
Example 2 cont. Solving analytically as it is a very simple DE:

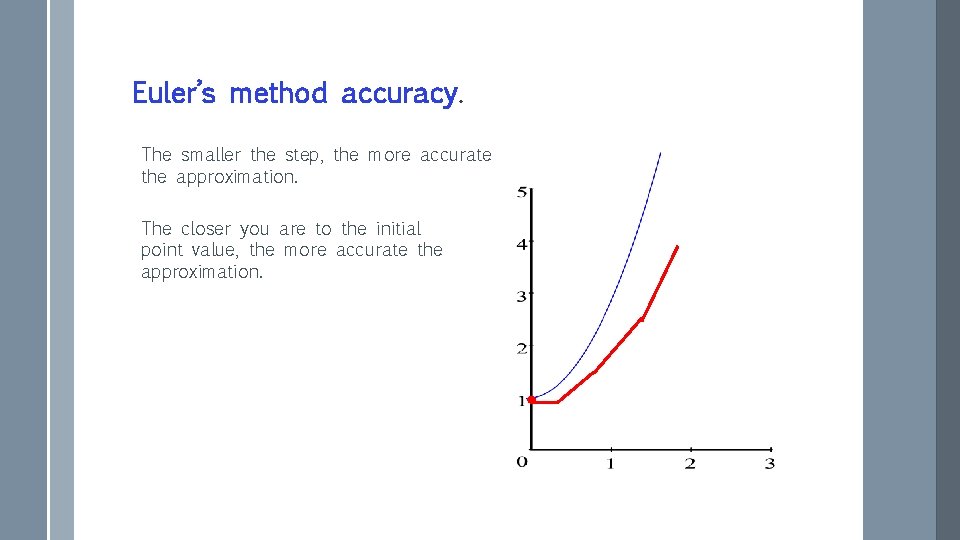
Euler’s method accuracy. The smaller the step, the more accurate the approximation. The closer you are to the initial point value, the more accurate the approximation.

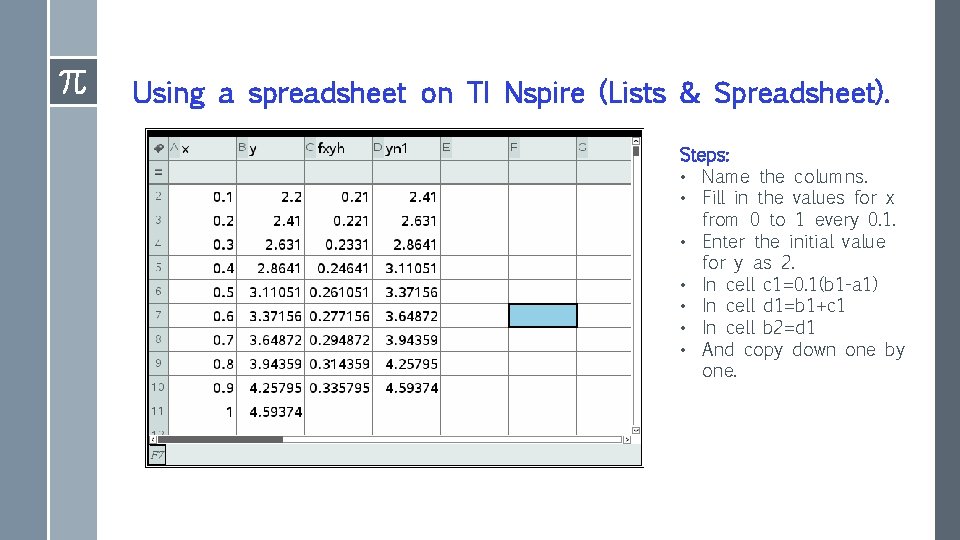
Using a spreadsheet on TI Nspire (Lists & Spreadsheet). Steps: • Name the columns. • Fill in the values for x from 0 to 1 every 0. 1. • Enter the initial value for y as 2. • In cell c 1=0. 1(b 1 -a 1) • In cell d 1=b 1+c 1 • In cell b 2=d 1 • And copy down one by one.

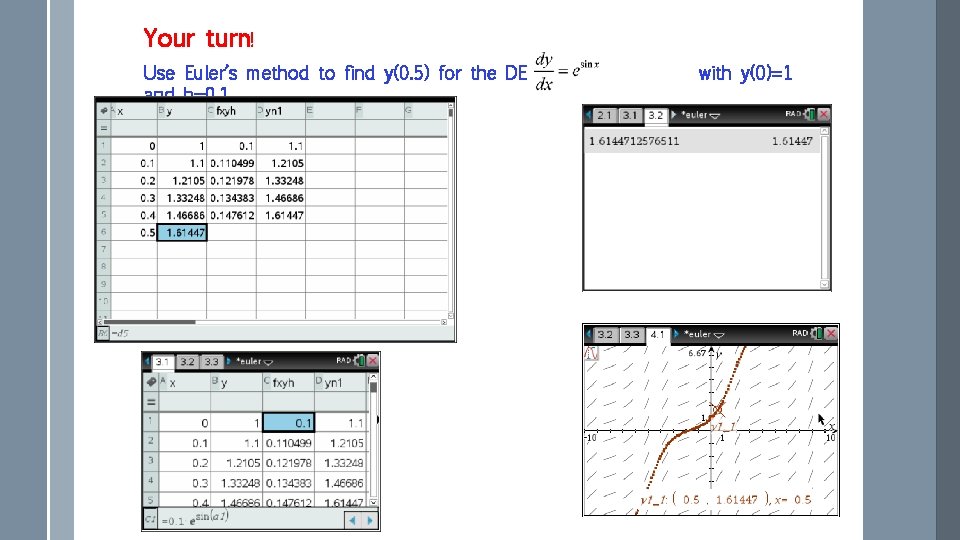
Your turn! Use Euler’s method to find y(0. 5) for the DE and h=0. 1 with y(0)=1

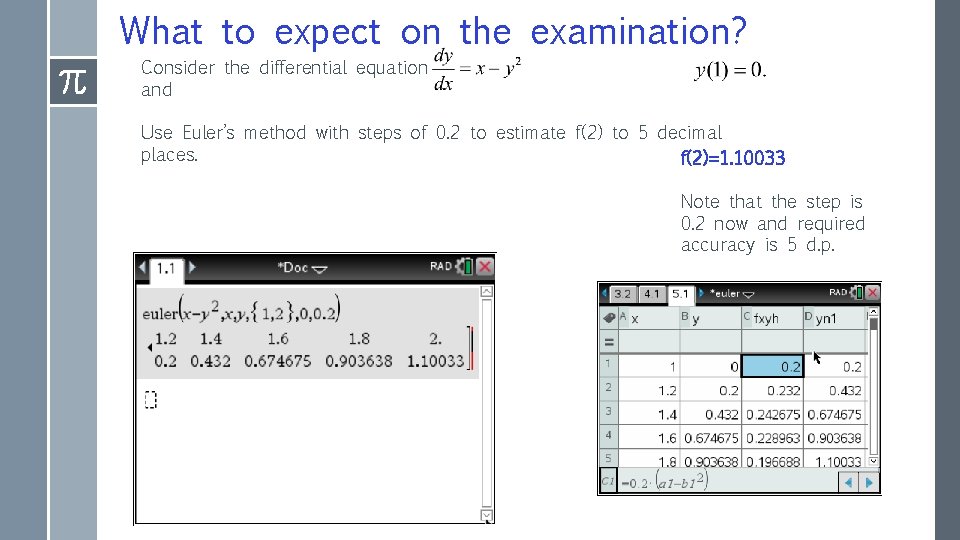
What to expect on the examination? Consider the differential equation and Use Euler’s method with steps of 0. 2 to estimate f(2) to 5 decimal places. f(2)=1. 10033 Note that the step is 0. 2 now and required accuracy is 5 d. p.

Change the float in 9: Settings Display Digits Float to display 5 d. p.

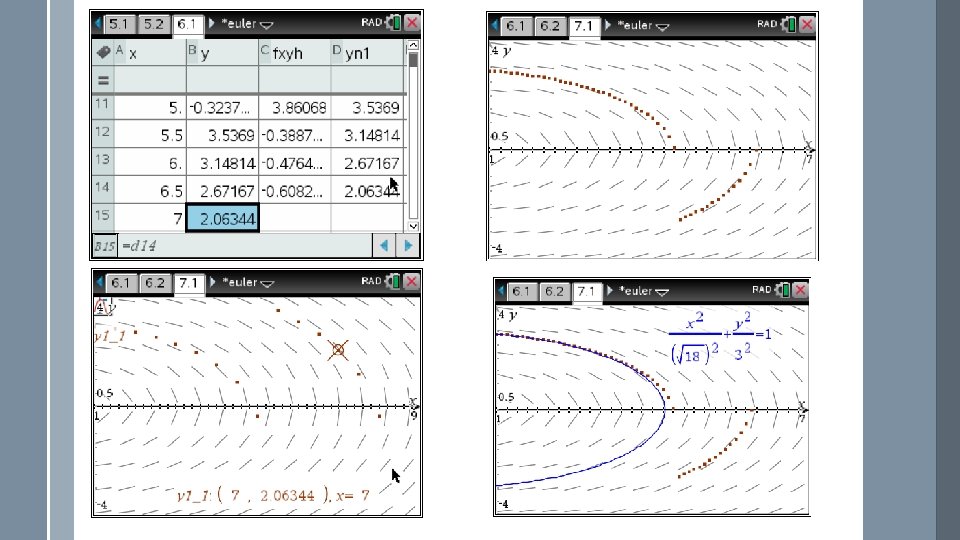
Question: (a) For the differential equation with y(0)=3, use the Euler’s method with step h=0. 5 to find y(7) to 4 decimal places. (b) Sketch the slope field for the above differential equation for x values from 0 to 7 and y values from -4 to 4. (c) Plot the pairs of x and y-values from your spreadsheet on the slope field graph. (d) For which values of x does the numerical solution by Euler’s method seem to follow the slope field? (e) For which values of x is the numerical method clearly wrong? (f) Solve the differential equation algebraically. (g) Plot the particular solution which contains (0, 3). (h) Explain why Euler’s method gives meaningless answers for larger values of x. Answers: (a) f(7)=2. 0634 (d) Euler’s method seems to produce reasonable answers for x<5 (f) 0. 5 x 2+y 2=9 (h) The solution curve is an ellipse with semi-major axis = 4. 24 (x-direction) and semi-minor axis =3 (y-direction). When the curve approaches the x-axis, the slope becomes nearly infinite. Furthermore, after crossing the x-axis the curve should go in the negative x-direction, but the method does not account for this.

Summary: › Describe Euler’s method for solving the intial value problem y’=f(x, y), y(x 0)=y 0. › Comment on the method’s accuracy. › Why might you want to solve an initial value problem numerically? › What is the slope field of a differential equation y’=f(x, y)? › What can we learn from such fields?