Special Types of Binary Relations Section 1 3

Special Types of Binary Relations Section 1. 3 Mon, Aug 30, 2004

Special Properties of Relations Let R be a binary relation on a set A. p R is reflexive if (a, a) R for all a A. p R is symmetric if, for all a, b A, (a, b) R (b, a) R. p R is transitive if, for all a, b, c A, (a, b) R and (b, c) R (a, c) R. p R is antisymmetric if, for all a, b A, (a, b) R and a b (b, a) R. p

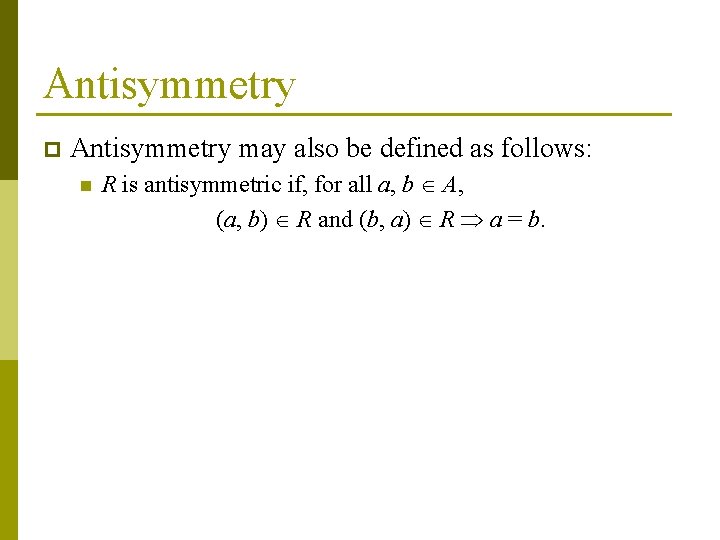
Antisymmetry p Antisymmetry may also be defined as follows: n R is antisymmetric if, for all a, b A, (a, b) R and (b, a) R a = b.

Graphs of Relations Given a relation R on a set A, create a directed graph G whose vertices are the members of A. p G will contain a directed edge (a, b) if and only if (a, b) R. p What property will the graph have if R is reflexive? p What property will the graph have if R is symmetric? p What property will the graph have if R is transitive? p What property will the graph have if R is antisymmetric? p

Equivalence Classes Let R be an equivalence relation on A and let a A. p The equivalence class of a is [a] = {b A | (a, b) R}. p Let A be the set of all (syntactically correct) computer programs. p Define a relation R as follows: p n n n (a, b) R if a and b always produce the same output for the same input. Let h be a program that prints “Hello, World!” What is [h]?

Equivalence Relations and Partitions Theorem: Let R be an equivalence relation on a set A. The equivalence classes of R form a partition of A. p Proof: p n n n Each set in the partition is nonempty since a [a] for all a. For the same reason, it is clear that the union of all the equivalence classes is all of A. It remains to show that distinct equivalence classes are disjoint. Suppose that [a] [b] . Then they have an element c in common.

Equivalence Relations and Partitions n n n n n The (a, c) R and (b, c) R since c [a] and c [b]. By symmetry, (c, b) R. By transitivity, (a, b) R. Now let d [b]. Then (b, d) R. It follows from transitivity that (a, d) R. So, d [a]. Therefore, [b] [a]. Similarly, we can show that [a] [b]. Therefore, [a] = [b].

Partial Orders A relation on a set A is a partial order if it is reflexive, antisymmetric, and transitive. p The standard example is the subset relation. p Another example is the divisor relation on positive integers. p

Total Orders A partial order R on a set A is a total order if it also has the property that, for all a, b A, either (a, b) R or (b, a) R. p The standard example is the less-than-or-equal-to relation on real numbers. p