Special Topics on Graph Algorithms Finding the Diameter

Special Topics on Graph Algorithms Finding the Diameter in Real-World Graphs Experimentally Turning a Lower Bound into an Upper Bound F 96943167 施信瑋 F 97943070 方劭云 R 98943086 莊舜翔 R 98943090 曹蕙芳 R 98943088 周邦彥 R 98921072 金 蘊 R 99921040 林國偉 R 99942061 葉書豪 1

Outline Introduction R 98943086 莊舜翔 Previous Work R 98943090 曹蕙芳 R 98943088 周邦彥 Finding the Diameter in Real-World Graphs R 99921040 林國偉 R 99942061 葉書豪 R 98943086 莊舜翔 Other Related Topics F 96943167 施信瑋 F 97943070 方劭云 Conclusion and Future Work R 98921072 金 蘊 2

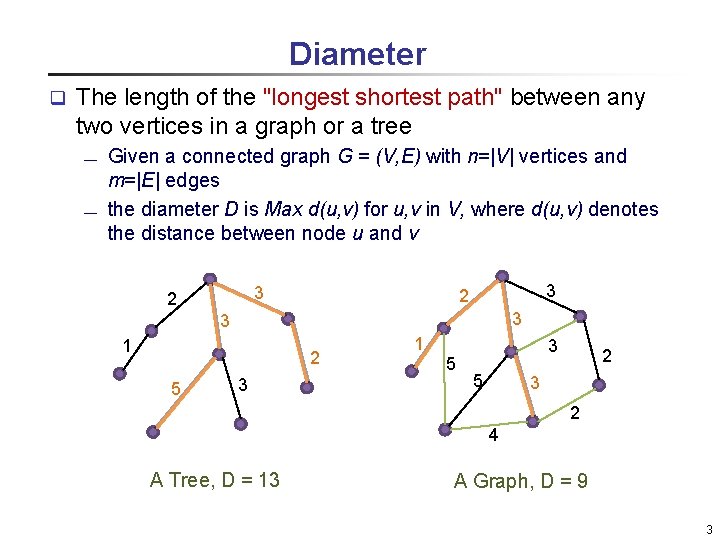
Diameter q The length of the "longest shortest path" between any two vertices in a graph or a tree ¾ ¾ Given a connected graph G = (V, E) with n=|V| vertices and m=|E| edges the diameter D is Max d(u, v) for u, v in V, where d(u, v) denotes the distance between node u and v 3 2 3 3 1 2 5 3 1 5 3 5 2 3 2 4 A Tree, D = 13 A Graph, D = 9 3

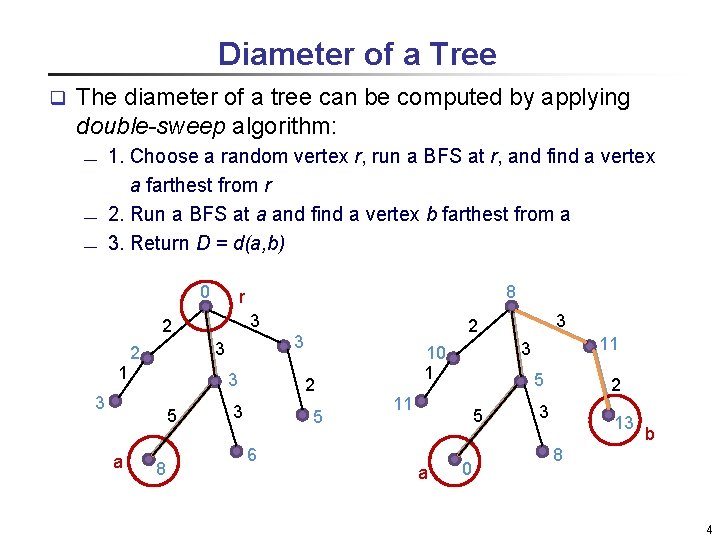
Diameter of a Tree q The diameter of a tree can be computed by applying double-sweep algorithm: 1. Choose a random vertex r, run a BFS at r, and find a vertex a farthest from r ¾ 2. Run a BFS at a and find a vertex b farthest from a ¾ 3. Return D = d(a, b) ¾ 0 3 2 1 3 3 5 8 2 3 5 6 3 2 3 3 2 a 8 r 5 11 5 a 11 3 10 1 0 2 3 13 b 8 4

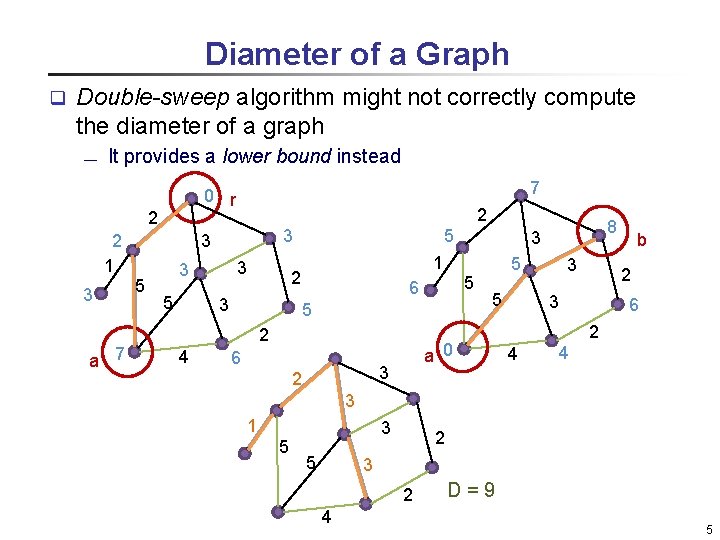
Diameter of a Graph q Double-sweep algorithm might not correctly compute the diameter of a graph ¾ It provides a lower bound instead 2 a 7 2 3 3 2 1 3 7 0 r 5 3 3 5 5 1 2 3 5 2 4 5 6 6 5 5 a 0 3 2 8 3 3 b 2 3 6 2 4 4 3 1 5 3 5 2 3 2 4 D = 9 5

Outline Introduction R 98943086 莊舜翔 Previous Work R 98943090 曹蕙芳 R 98943088 周邦彥 Finding the Diameter in Real-World Graphs R 99921040 林國偉 R 99942061 葉書豪 R 98943086 莊舜翔 Other Related Topics F 96943167 施信瑋 F 97943070 方劭云 Conclusion and Future Work R 98921072 金 蘊 6

Naïve Algorithm q Perform n breadth-first searches (BFS) from each vertex to obtain distance matrix of the graph ¾ q Θ(n(n+m)) time and Θ(m) space By using matrix multiplication, the distance matrix can be computed in O(M(n)logn) time and Θ(n 2) space [Seidel, ACM STC’ 92] ¾ M(n): the complexity for matrix multiplication involving small integers only (O(n 2. 376)) Is too slow for massive graphs and has a prohibitive space cost 7

All Pairs Shortest Path q Compute the distances between all pairs of vertices without resorting to matrix products ¾ ¾ [Feder, ACM STC’ 91]: Θ(n 3 / logn) time and O(n 2) space [Chan, ACM-SIAM’ 06]: O(n 2(loglogn)2 / logn) time and O(n 2) space Still too slow and space consuming for massive graphs 8

All Pairs Almost Shortest Path (1/2) q Compute almost shortest paths between all pairs of vertices [Dor, ECCC’ 97] ¾ ¾ Additive error 2 Treat high-degree vertices and low-degree vertices separately 9

All Pairs Almost Shortest Path (2/2) q w’ Additive error 2: apasp 2 u w v w’ u ¾ w v O(min(n 3/2 m 1/2, n 7/3)logn) time and Θ(n 2) space Still too expensive 10

Self-checking Heuristics Too expensive to obtain the exact value or accurate estimations of the diameter for massive graphs Empirically establish some lower and upper bounds by executing a suitable small number of BFS q L ≦ D ≦ U ¾ Obtain the actual value of D for G when L = U Self-checking heuristics ¾ 11

Self-checking Heuristics q No guarantee of success for every feasible input, BUT ¾ ¾ ¾ 1) It requires few BFSes in practice, and thus its complexity is linear [Magnien, JEA’ 09] 2) An empirical upper bound is possible 3) Large graphs can be analyzed n since BFS has a good external-memory implementation [Mayer, AESA’ 02] and works on graphs stored in compressed format [Vigna, IWWWC’ 04] 12

A Comparing Work q “Fast Computation of Empirically Tight Bounds for the Diameter of Massive Graphs” [Magnien, JEA’ 09] ¾ ¾ Various bounds to confine the solution range n Trivial bounds n Double sweep lower bound n Tree upper bound Iterative algorithm to obtain the actual diameter 13

Trivial Bounds q The eccentricity of any vertex v gives trivial bounds of the diameter: ecc(v) ≤ D ≤ 2 • ecc(v) q Trivial bounds can be computed in Θ(m) space and time, where m is the number of edges in the graph q D ≤ 2 • ecc(v) ¾ ¾ ¾ If D > 2 • ecc(v), then max(ecc(v)) > 2 • ecc(v) We can choose a center point in the diameter that contradicts the derived inequality Therefore, D ≤ 2 • ecc(v) 14

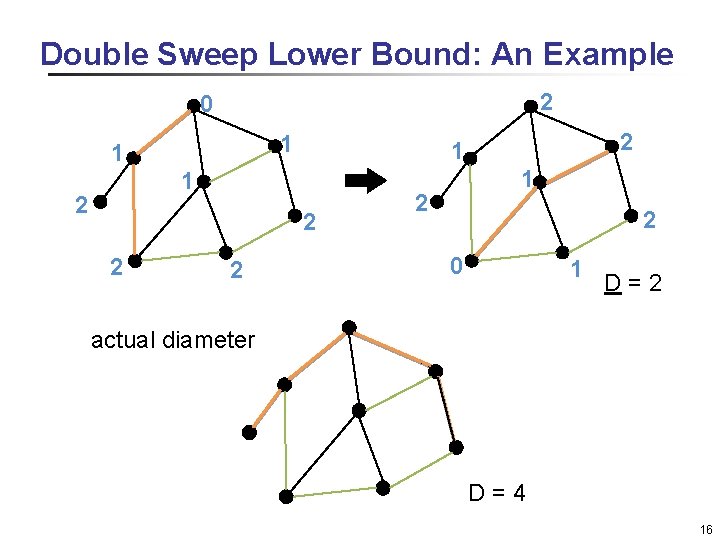
Double Sweep Lower Bound q On chordal graphs, AT-free graphs, and tree graphs, if a vertex v is chosen such that d(u, v) = ecc(u) for a vertex u, then D = ecc(u) (i. e. v is among the vertices which are at maximal distance from u) [Corneil’ 01, Handler’ 73] ¾ q The diameter may therefore be computed by a BFS from any node u and then a BFS from a node at maximal distance from u, thus in Θ(m) space and time, where m is the number of edges. Generally, the value obtained in this way may different from the diameter, but still better than trivial lower bounds 15

Double Sweep Lower Bound: An Example 2 0 1 1 1 2 2 2 1 1 2 2 0 1 D = 2 actual diameter D = 4 16

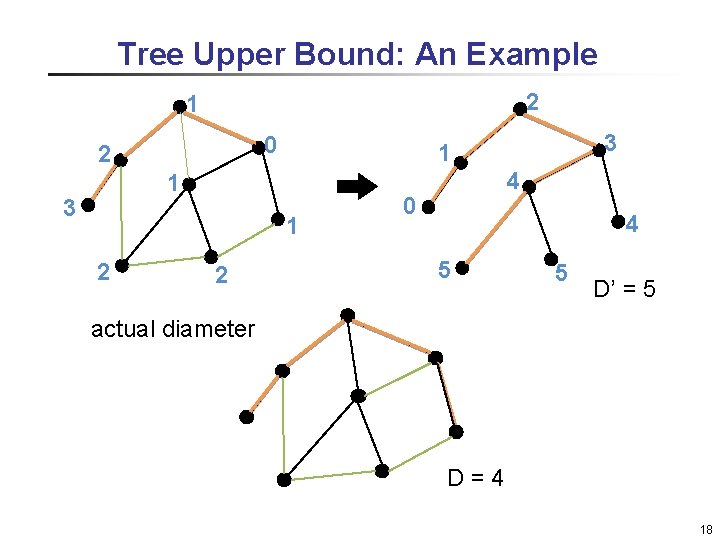
Tree Upper Bound The diameter of any spanning connected subgraph of G is larger than or equal to the diameter of G q Tree diameter can be obtain in Θ(m) time and space [Handler’ 73], where m is the number of edges in G q ¾ Spanning trees of G, are good candidates for obtaining an upper bound A tree upper bound is the diameter of a BFS tree from a vertex q It is always better than the corresponding trivial upper bound q 17

Tree Upper Bound: An Example 2 1 0 2 1 3 1 2 2 3 1 4 0 4 5 5 D’ = 5 actual diameter D = 4 18

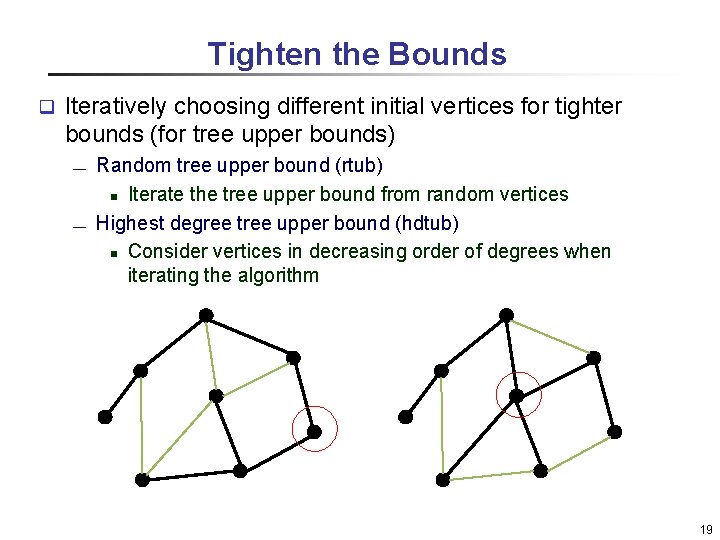
Tighten the Bounds q Iteratively choosing different initial vertices for tighter bounds (for tree upper bounds) ¾ ¾ Random tree upper bound (rtub) n Iterate the tree upper bound from random vertices Highest degree tree upper bound (hdtub) n Consider vertices in decreasing order of degrees when iterating the algorithm 19

The Iterative Algorithm Iterate the double sweep lower bound and highest degree tree upper bound until the difference between the best bounds obtained is lower than or equal to a given threshold value q Multiple choices for this threshold value q ¾ Depending factors: the graph considered, the desired quality of the bounds, or even set the threshold to be a given precision (e. g. D’-D/D<p) q All heuristics have a Θ(m) time complexity, and a Θ(m+n) space complexity. q Does the tree upper bound eventually converge to the exact diameter? 20

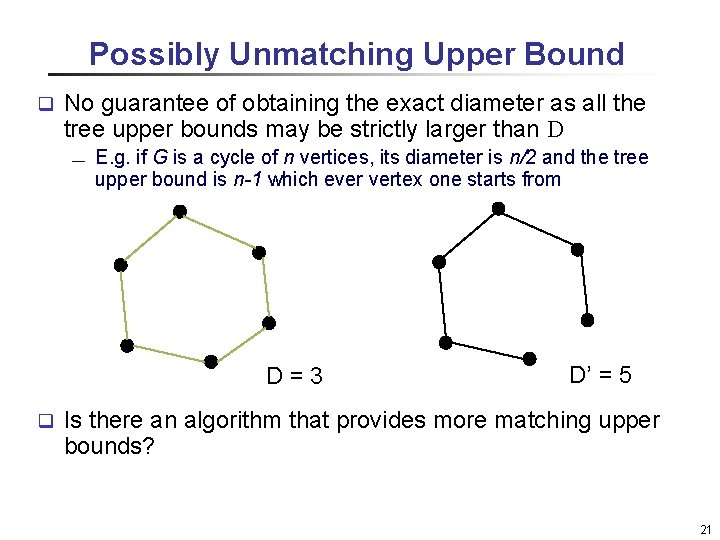
Possibly Unmatching Upper Bound q No guarantee of obtaining the exact diameter as all the tree upper bounds may be strictly larger than D ¾ E. g. if G is a cycle of n vertices, its diameter is n/2 and the tree upper bound is n-1 which ever vertex one starts from D = 3 q D’ = 5 Is there an algorithm that provides more matching upper bounds? 21

Outline Introduction R 98943086 莊舜翔 Previous Work R 98943090 曹蕙芳 R 98943088 周邦彥 Finding the Diameter in Real-World Graphs R 99921040 林國偉 R 99942061 葉書豪 R 98943086 莊舜翔 Other Related Topics F 96943167 施信瑋 F 97943070 方劭云 Conclusion and Future Work R 98921072 金 蘊 22

The Fringe Algorithm q Fringe method is used to improve the upper bound U and possibly match the lower bound L obtained by the double sweep method 23

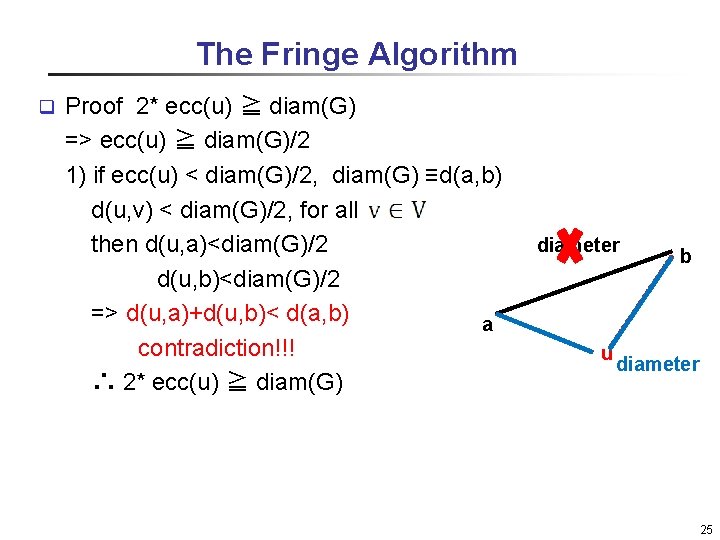
The Fringe Algorithm An unweighted, undirected and connected graph G=( V, E ) q For any vertex Tu denotes an unordered BFS-tree Eccentricity ecc(u) is the height of Tu => 2* ecc(u) ≧ diam(G) q 24

The Fringe Algorithm Proof 2* ecc(u) ≧ diam(G) => ecc(u) ≧ diam(G)/2 1) if ecc(u) < diam(G)/2, diam(G) ≡d(a, b) d(u, v) < diam(G)/2, for all then d(u, a)<diam(G)/2 d(u, b)<diam(G)/2 => d(u, a)+d(u, b)< d(a, b) a contradiction!!! ∴ 2* ecc(u) ≧ diam(G) q diameter u b diameter 25

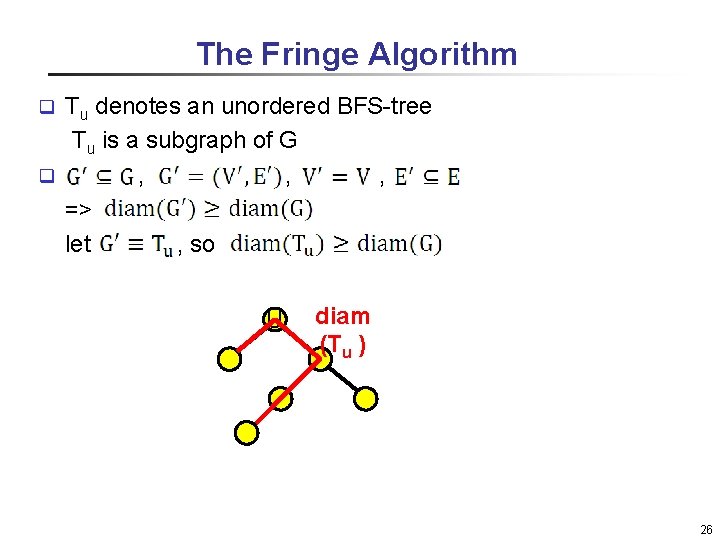
The Fringe Algorithm Tu denotes an unordered BFS-tree Tu is a subgraph of G q , , => let , so q U diam (Tu ) 26

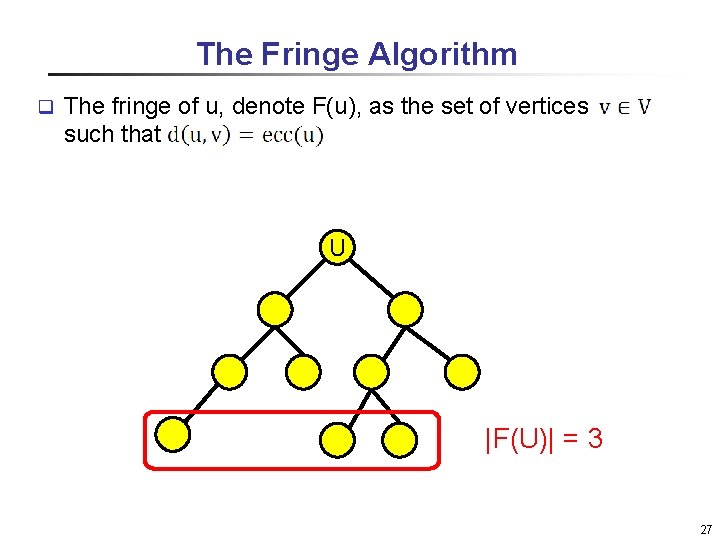
The Fringe Algorithm q The fringe of u, denote F(u), as the set of vertices such that U |F(U)| = 3 27

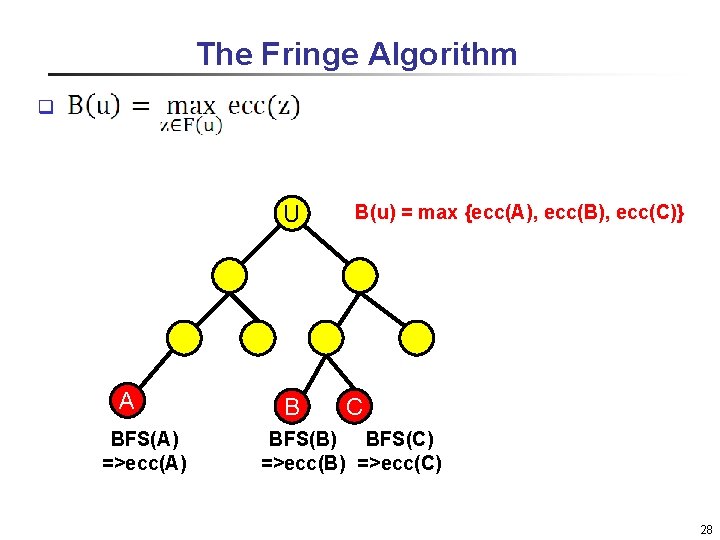
The Fringe Algorithm q U A BFS(A) =>ecc(A) B B(u) = max {ecc(A), ecc(B), ecc(C)} C BFS(B) BFS(C) =>ecc(B) =>ecc(C) 28

The Fringe Algorithm The fringe of u, denote F(u), as the set of vertices such that q q q 29

The Fringe Algorithm q Lemma. U(u) ≧D, where D is the diameter of G q 30

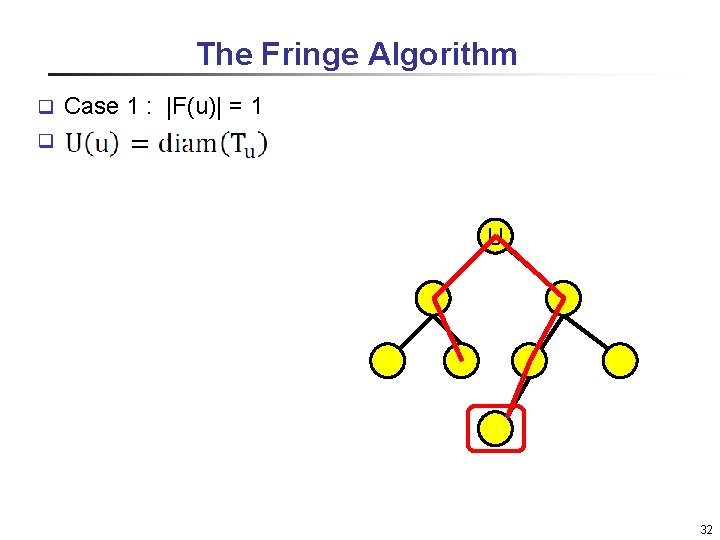
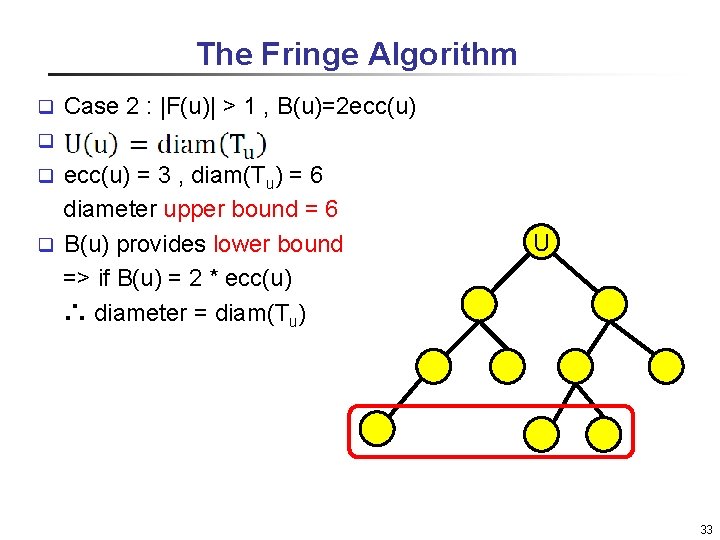
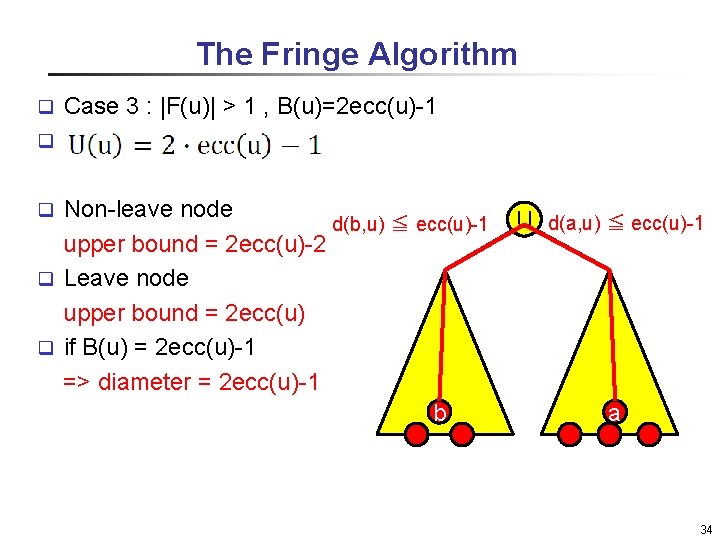
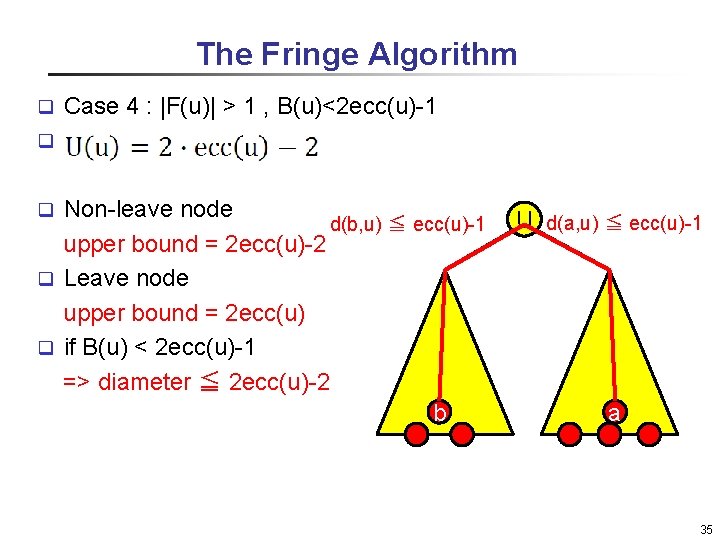
The Fringe Algorithm Case 1 : |F(u)| = 1 => q Case 2 : |F(u)| > 1 , B(u)=2 ecc(u) => q Case 3 : |F(u)| > 1 , B(u)=2 ecc(u)-1 => q Case 4 : |F(u)| > 1 , B(u)<2 ecc(u)-1 => q 31

The Fringe Algorithm Case 1 : |F(u)| = 1 q q U 32

The Fringe Algorithm Case 2 : |F(u)| > 1 , B(u)=2 ecc(u) q q ecc(u) = 3 , diam(Tu) = 6 diameter upper bound = 6 q B(u) provides lower bound => if B(u) = 2 * ecc(u) ∴ diameter = diam(Tu) q U 33

The Fringe Algorithm Case 3 : |F(u)| > 1 , B(u)=2 ecc(u)-1 q q Non-leave node d(b, u) ≦ ecc(u)-1 upper bound = 2 ecc(u)-2 q Leave node upper bound = 2 ecc(u) q if B(u) = 2 ecc(u)-1 => diameter = 2 ecc(u)-1 b q U d(a, u) ≦ ecc(u)-1 a 34

The Fringe Algorithm Case 4 : |F(u)| > 1 , B(u)<2 ecc(u)-1 q q Non-leave node d(b, u) ≦ ecc(u)-1 upper bound = 2 ecc(u)-2 q Leave node upper bound = 2 ecc(u) q if B(u) < 2 ecc(u)-1 => diameter ≦ 2 ecc(u)-2 b q U d(a, u) ≦ ecc(u)-1 a 35

The Fringe Algorithm q The fringe algorithm correctly computes an upper bound for the diameter of the input graph G, using at most |F(u)|+3 BFS. 36

The Fringe Algorithm Let r, a, and b be the vertices identified by double sweep(using two BFSes) q Find the vertex u that is halfway along the path connecting a and b inside the BFS-tree Ta q Compute the BFS-tree Tu and its eccentricity ecc(u) q If |F(u)|>1, find the BFS-tree Tz for each and compute B(u) q ¾ ¾ q If B(u)=2 ecc(u)-1, return 2 ecc(u)-1 If B(u)<2 ecc(u)-1, return 2 ecc(u)-2 Return the diameter(Tu) 37

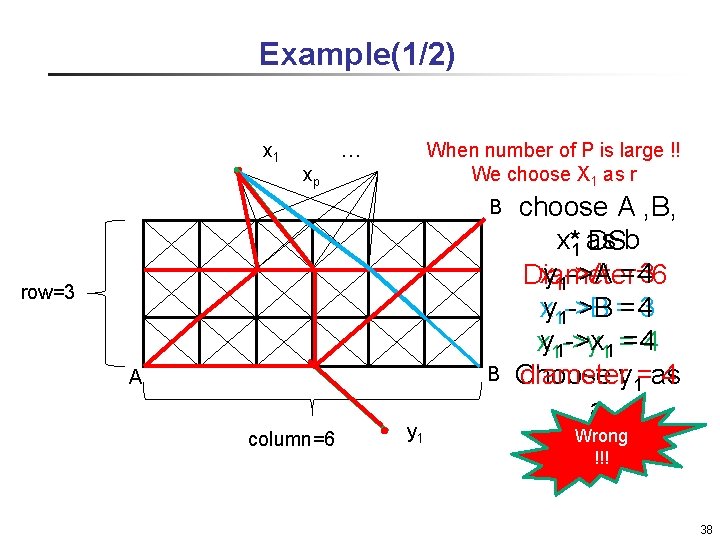
Example(1/2) x 1 … When number of P is large !! xp We choose X 1 as r B row=3 B A column=6 y 1 choose A , B, x* DS 1 as b ->A =4 xy 11 ->A = 3 Diameter=6 ->B =4 xy 11 ->B = 3 ->x 11 = 4 =4 xy 11 ->y diameter = 4 Choose y 1 as a Wrong !!! 38

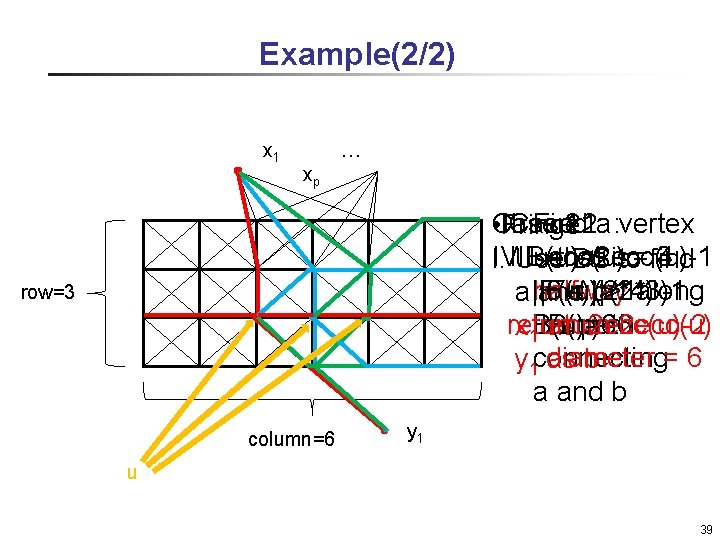
Example(2/2) x 1 … xp Case 2 : Case 1 : Case 2 : II. Find a vertex • Case 1 : Fringe IV. B(u)<2 ecc(u)-1 IV. B(u)=2 ecc(u) III. ecc(u) = 4 III. ecc(u) = 3 u that is I. Use DS to find 6 < (2*4) -1 6 = (2*3) |F(u)|>1 halfway along a and b return 2 ecc(u)-2 return 2 ecc(u) B(u)=6 the path x 1 as a diameter = 6 connecting y 1 as b a and b row=3 column=6 y 1 u 39

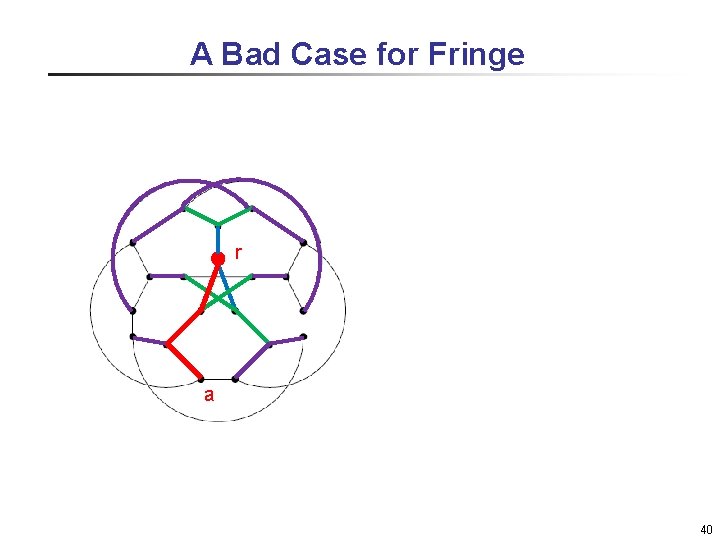
A Bad Case for Fringe r a 40

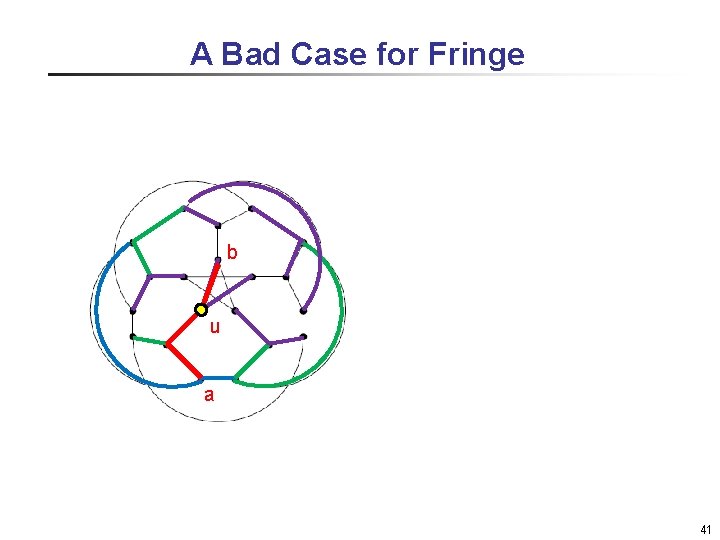
A Bad Case for Fringe b u a 41

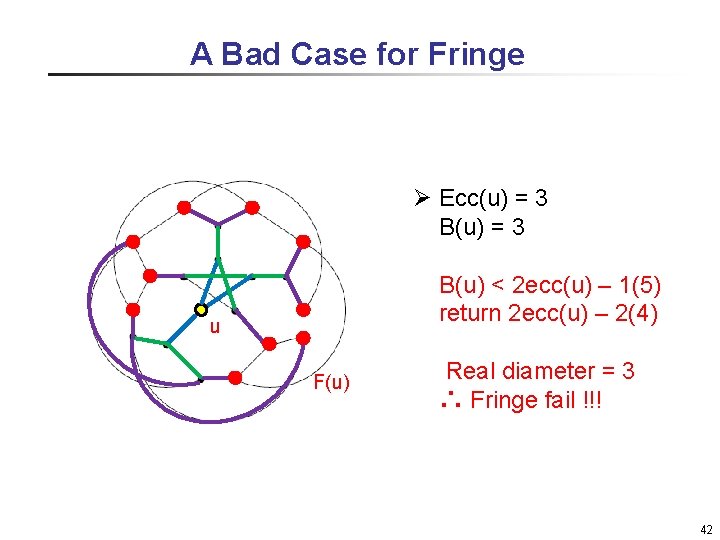
A Bad Case for Fringe Ø Ecc(u) = 3 B(u) = 3 u F(u) B(u) < 2 ecc(u) – 1(5) return 2 ecc(u) – 2(4) Real diameter = 3 ∴ Fringe fail !!! 42

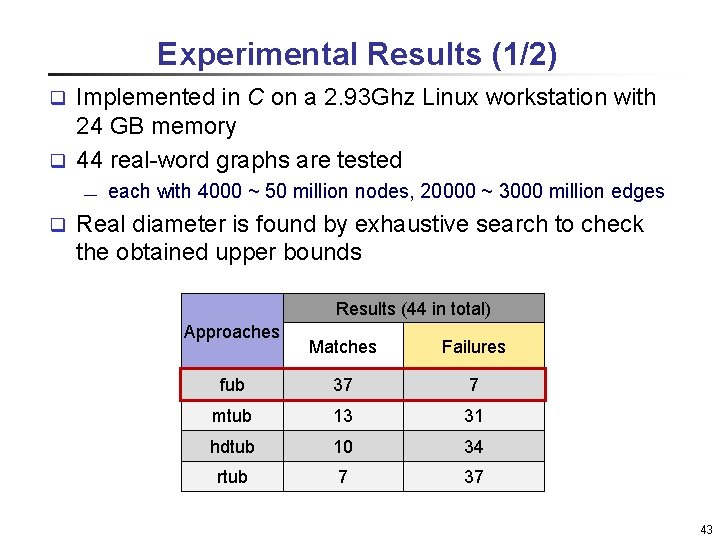
Experimental Results (1/2) Implemented in C on a 2. 93 Ghz Linux workstation with 24 GB memory q 44 real-word graphs are tested q ¾ q each with 4000 ~ 50 million nodes, 20000 ~ 3000 million edges Real diameter is found by exhaustive search to check the obtained upper bounds Results (44 in total) Approaches Matches Failures fub 37 7 mtub 13 31 hdtub 10 34 rtub 7 37 43

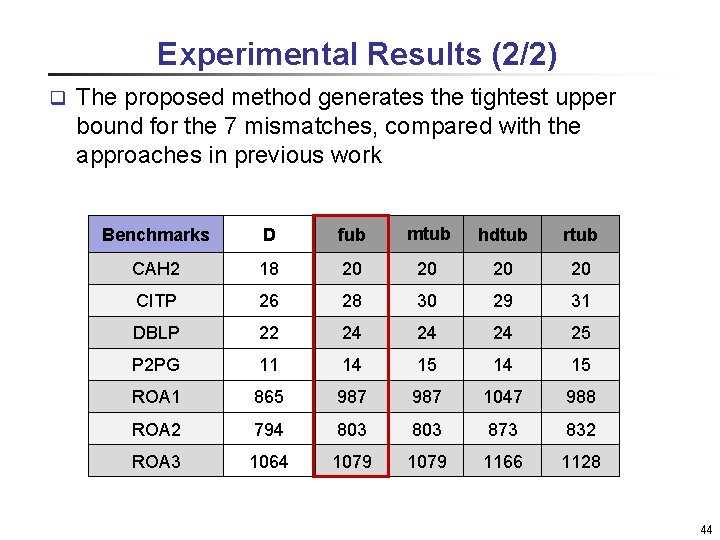
Experimental Results (2/2) q The proposed method generates the tightest upper bound for the 7 mismatches, compared with the approaches in previous work Benchmarks D fub mtub hdtub rtub CAH 2 18 20 20 CITP 26 28 30 29 31 DBLP 22 24 24 24 25 P 2 PG 11 14 15 ROA 1 865 987 1047 988 ROA 2 794 803 873 832 ROA 3 1064 1079 1166 1128 44

Outline Introduction R 98943086 莊舜翔 Previous Work R 98943090 曹蕙芳 R 98943088 周邦彥 Finding the Diameter in Real-World Graphs R 99921040 林國偉 R 99942061 葉書豪 R 98943086 莊舜翔 Other Related Topics F 96943167 施信瑋 F 97943070 方劭云 Conclusion and Future Work R 98921072 金 蘊 45

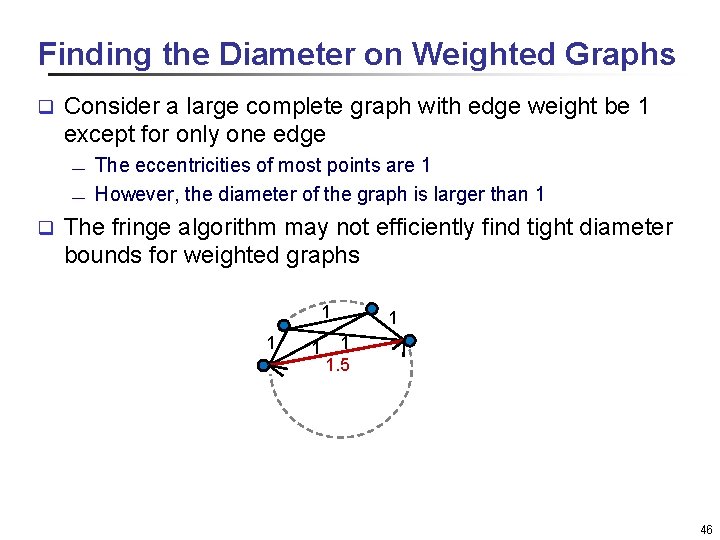
Finding the Diameter on Weighted Graphs q Consider a large complete graph with edge weight be 1 except for only one edge ¾ ¾ q The eccentricities of most points are 1 However, the diameter of the graph is larger than 1 The fringe algorithm may not efficiently find tight diameter bounds for weighted graphs 1 1 1. 5 46

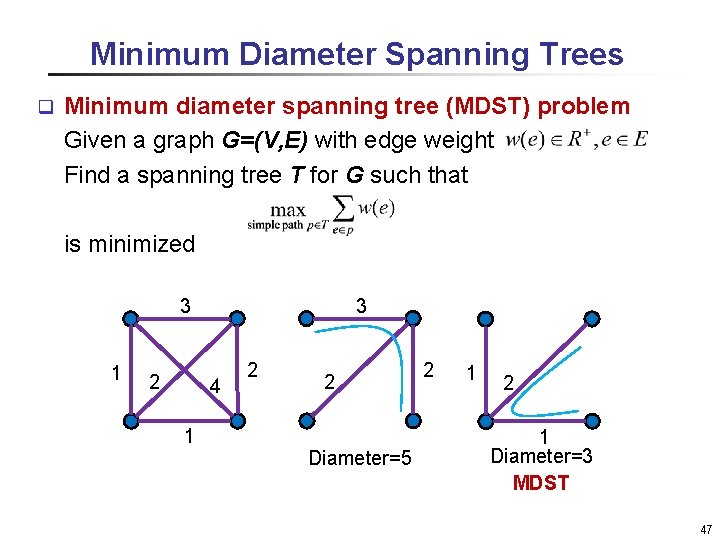
Minimum Diameter Spanning Trees q Minimum diameter spanning tree (MDST) problem Given a graph G=(V, E) with edge weight Find a spanning tree T for G such that is minimized 3 3 1 2 4 1 2 2 Diameter=5 2 1 Diameter=3 MDST 47

Outline Introduction Previous Work Finding the Diameter in Real-World Graphs R 98943086 莊舜翔 R 98943090 曹蕙芳 R 98943088 周邦彥 R 99921040 林國偉 R 99942061 葉書豪 R 98943086 莊舜翔 Other Related Topics Geometric MDST F 97943070 方劭云 MDST F 96943167 施信瑋 Conclusion and Future Work R 98921072 金 蘊 48

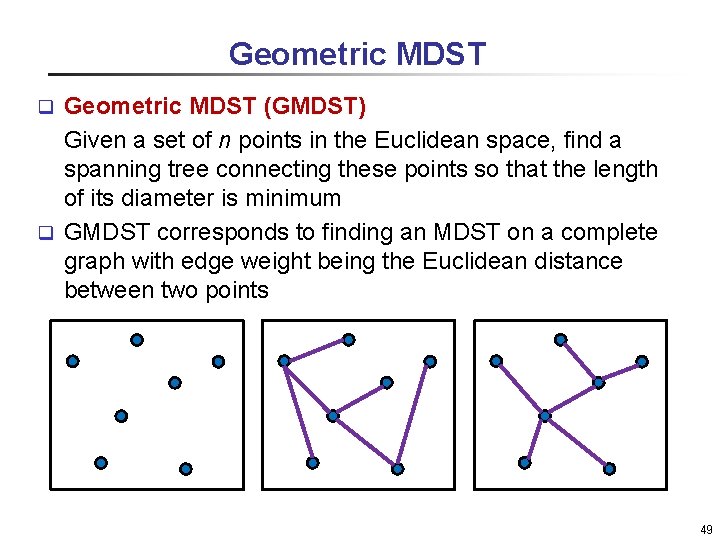
Geometric MDST (GMDST) Given a set of n points in the Euclidean space, find a spanning tree connecting these points so that the length of its diameter is minimum q GMDST corresponds to finding an MDST on a complete graph with edge weight being the Euclidean distance between two points q 49

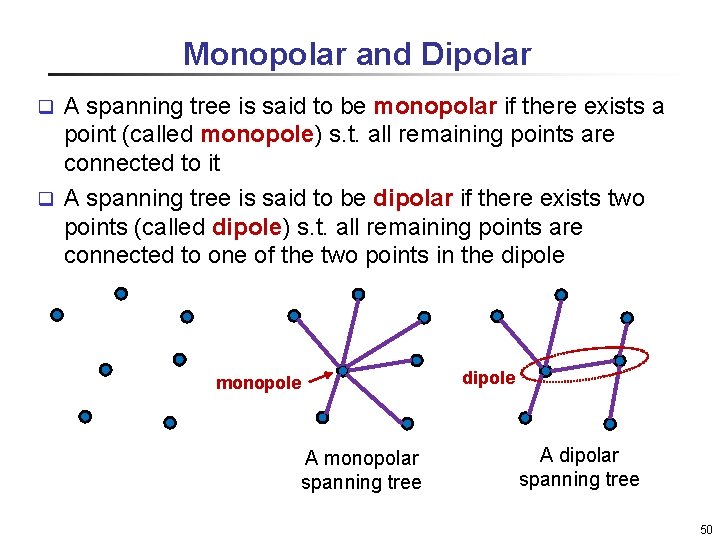
Monopolar and Dipolar A spanning tree is said to be monopolar if there exists a point (called monopole) s. t. all remaining points are connected to it q A spanning tree is said to be dipolar if there exists two points (called dipole) s. t. all remaining points are connected to one of the two points in the dipole q monopole A monopolar spanning tree dipole A dipolar spanning tree 50

GMDST with a Simple Topology q Theorem There exists a GMDST of a set S of n points which is either monopolar (n≧ 3) or dipolar (n≧ 4) All monopolar spanning trees of the 4 points 4 dipolar spanning trees of the 4 points 51

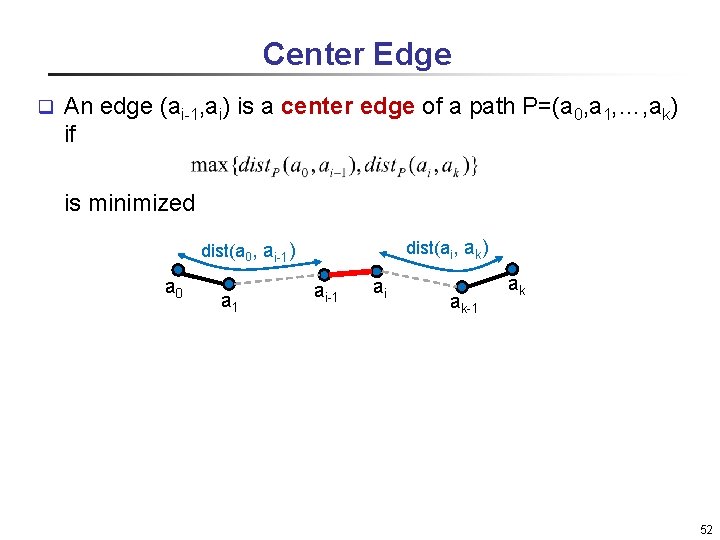
Center Edge q An edge (ai-1, ai) is a center edge of a path P=(a 0, a 1, …, ak) if is minimized dist(ai, ak) dist(a 0, ai-1) a 0 a 1 ai-1 ai ak-1 ak 52

Lemma q Lemma Let (ai-1, ai) be a center edge of a path P=(a 0, a 1, …, ak), then: (1) and (2) dist(ai-1, ak) dist(a 0, ai-1) a 0 a 1 ei-2 ai-1 ei-1 ai ai-2 ak-1 ak Otherwise, the center edge is not (ai-1, ai) B A a 0 a 1 ai-2 ei-1 a ai-1 i ak-1 ak If A > B: max{ A, B-ei-1 } > max{ A-ei-2, B } 53

Proof of the Theorem There exists a GMDST of a set S of n points which is either monopolar or dipolar q Proof q ¾ Case 1 Given any optimal GMDST T with a diameter composed of only two edges, i. e. , D(T) = (a 0, a 1, a 2) of size DT, a monopolar spanning tree T’ can be constructed with the same diameter a 1 a 0 Optimal T v u a 1 a 0 T’ a 2 u v 54

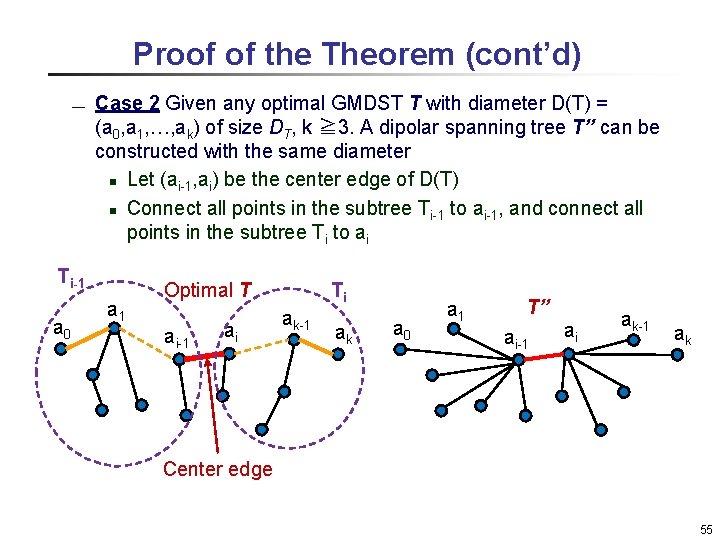
Proof of the Theorem (cont’d) ¾ Case 2 Given any optimal GMDST T with diameter D(T) = (a 0, a 1, …, ak) of size DT, k ≧ 3. A dipolar spanning tree T’’ can be constructed with the same diameter n Let (ai-1, ai) be the center edge of D(T) n Connect all points in the subtree Ti-1 to ai-1, and connect all points in the subtree Ti to ai Ti-1 a 0 a 1 Optimal T ai-1 ai Ti ak-1 ak a 0 a 1 T’’ ai-1 ai ak-1 ak Center edge 55

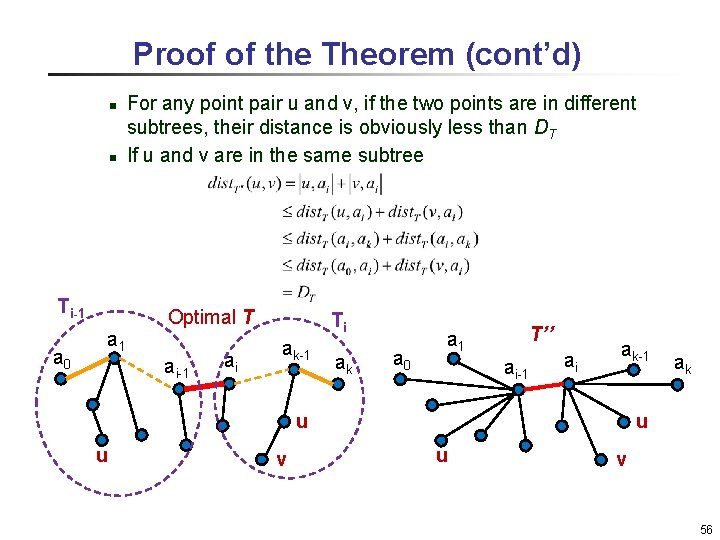
Proof of the Theorem (cont’d) n n Ti-1 a 0 a 1 For any point pair u and v, if the two points are in different subtrees, their distance is obviously less than DT If u and v are in the same subtree Optimal T ai-1 ai Ti ak-1 ak a 0 T’’ a 1 ai-1 ai ak-1 u u v ak u u v 56

Finding a Geometric MDST Theorem There exists a GMDST of a set S of n points which is either monopolar or dipolar q By enumerating all monopolar and dipolar spanning trees of a set of given points, an optimal GMDST can be found q The enumeration process can be done in θ(n 3) q 57

Outline Introduction R 98943086 莊舜翔 Previous Work R 98943090 曹蕙芳 R 98943088 周邦彥 Finding the Diameter in Real-World Graphs R 99921040 林國偉 R 99942061 葉書豪 R 98943086 莊舜翔 Other Related Topics Geometric MDST F 97943070 方劭云 MDST F 96943167 施信瑋 Conclusion and Future Work R 98921072 金 蘊 58

Introduction [Ho et al. , SIAMJ’ 91] solved the geometric MDST in O(n 3) q Actually, the general MDST problem is identical to the absolute 1 -center problem (A 1 CP) q The absolute 1 -center problem q For , Let Find x=x* such that F(x) is minimized 59

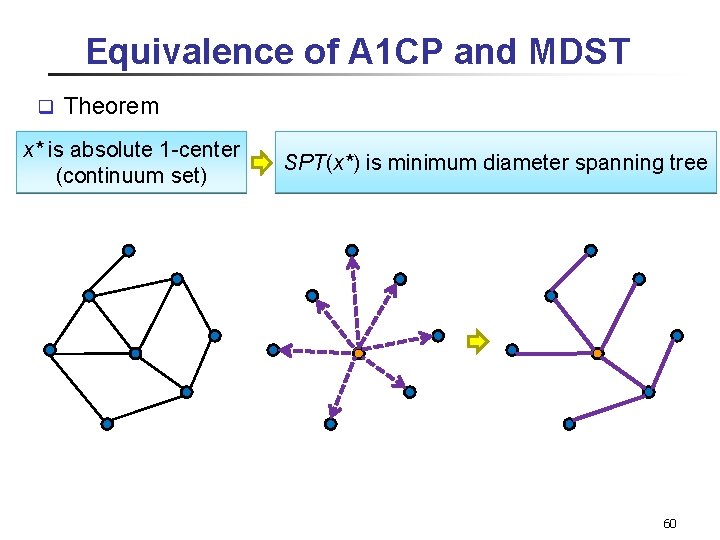
Equivalence of A 1 CP and MDST q Theorem x* is absolute 1 -center (continuum set) SPT(x*) is minimum diameter spanning tree 60

The Proof of Equivalence q Proof idea ¾ ¾ ¾ q Considering metric space solution with continuum set SPT(y*) Diameter of SPT(x*) equals to that of SPT(y*) As SPT(y*) is minimum, the MDST is solved Continuum set ¾ ¾ Let the graph be rectifiable Refer interior points on an edge by their distances from the two nodes 3 5 10 7 5 61

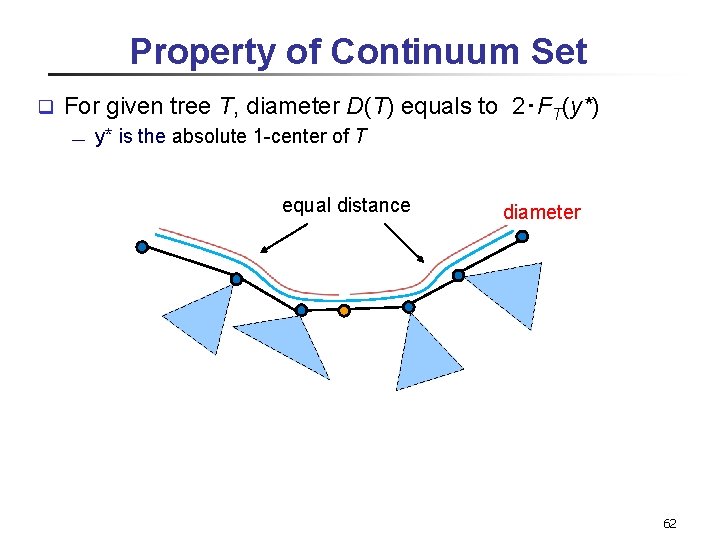
Property of Continuum Set q For given tree T, diameter D(T) equals to 2‧FT(y*) ¾ y* is the absolute 1 -center of T equal distance diameter 62

Proof q Assume that z* is the absolute 1 -center of G ¾ By following the property of continuum set, ¾ Since the tree is the shortest path tree rooted at z*, ¾ Since z* is the absolute 1 -center of G, ¾ For any tree Ti rooted at u, ¾ It implies that, for any spanning tree Tj , 63

Conclusion q The concepts of monopolar and dipolar [Ho et al. , SIAMJ’ 91] are exactly the same as the proved result monopole dipole absolute 1 -center q By using all pairs shortest distance [Fredman and Tarjan, JACM’ 87], the A 1 CP can be solved in O(mn + n 2 log n) 64

Outline Introduction R 98943086 莊舜翔 Previous Work R 98943090 曹蕙芳 R 98943088 周邦彥 Finding the Diameter in Real-World Graphs R 99921040 林國偉 R 99942061 葉書豪 R 98943086 莊舜翔 Other Related Topics F 96943167 施信瑋 F 97943070 方劭云 Conclusion and Future Work R 98921072 金 蘊 65

Conclusion q In today’s presentation, we have ¾ ¾ ¾ Introduce the difference between finding the diameter on a tree and finding the diameter on a general graph Give some naïve algorithms for finding the diameter on a graph Present the double sweep algorithm introduced in the previous work Present the fringe algorithm which extends the double sweep algorithm Compare the double sweep algorithm and the fringe algorithm 66

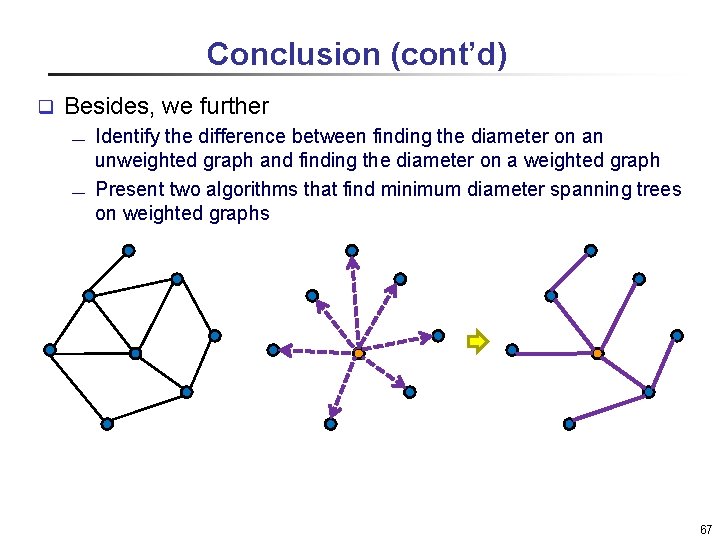
Conclusion (cont’d) q Besides, we further ¾ ¾ Identify the difference between finding the diameter on an unweighted graph and finding the diameter on a weighted graph Present two algorithms that find minimum diameter spanning trees on weighted graphs 67

Future Work q Another topic related to the design methodology for directed graphs with minimum diameter is interesting as well ¾ ¾ q “Design to minimize diameter on building-block network”, Makoto Imase and Masaki Itoh “A design for directed graphs with minimum diamter”, Makoto Imase and Masaki Itoh Given # nodes and the upper bounds of in- and outdegree, design a directed graph s. t. the diameter is minimized n = 9, d = 2 68

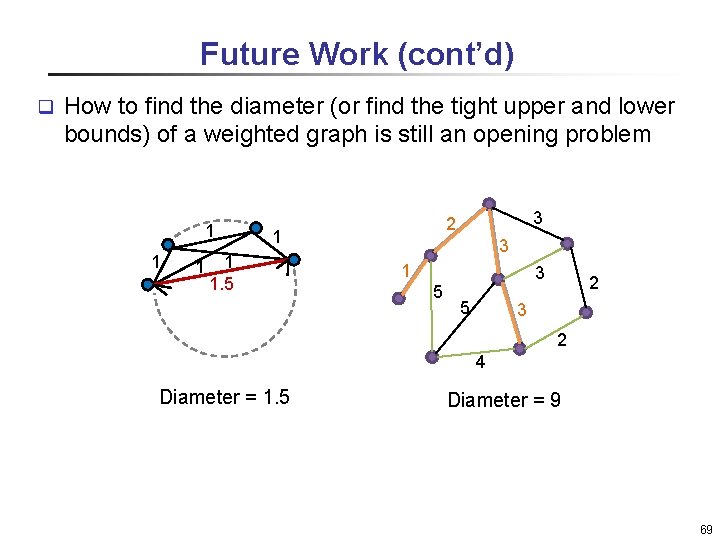
Future Work (cont’d) q How to find the diameter (or find the tight upper and lower bounds) of a weighted graph is still an opening problem 1 1 1. 5 3 2 3 1 5 3 5 2 3 2 4 Diameter = 1. 5 Diameter = 9 69