Special Theory of Relativity Special Relativity I Einsteins

Special Theory of Relativity

Special Relativity I • • • Einstein’s postulates Simultaneity Time dilation Length contraction New velocity addition law

I: EINSTEIN’S POSTULATES OF RELATIVITY • Postulate 1 – The laws of nature are the same in all inertial frames of reference • Postulate 2 – The speed of light in a vacuum is the same in all inertial frames of reference. • Let’s start to think about the consequences of these postulates. • We will perform “thought experiments” (Gedankenexperiment)… • For now, we will ignore effect of gravity – we suppose we are performing these experiments in the middle of deep space

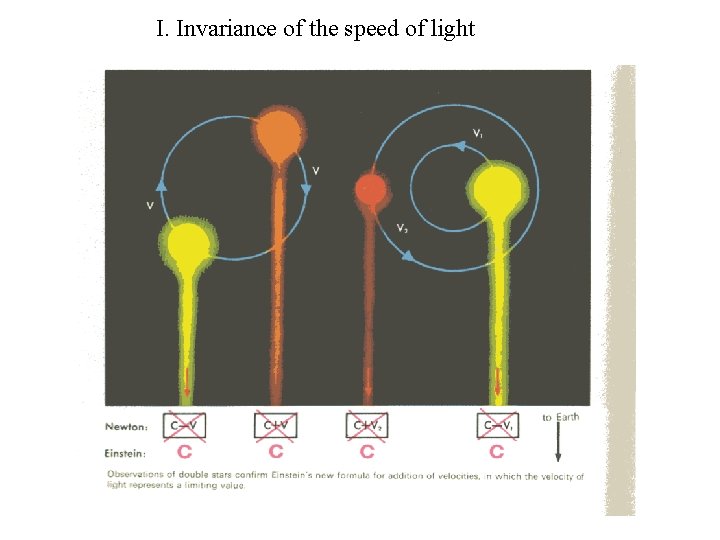
I. Invariance of the speed of light

II. Simultaneity

III: TIME DILATION A light clock consists of two parallel mirrors and a photon bouncing back and forth over the distance D. An observer at rest with the clock will measure a click at times Dto= 2 H/c

• Now suppose we put one clock on a train or spaceship that is cruising (at constant velocity, v) past us. • How long will it take the clock to “tick” when its in the moving spacecraft? Use Einstein’s postulates…

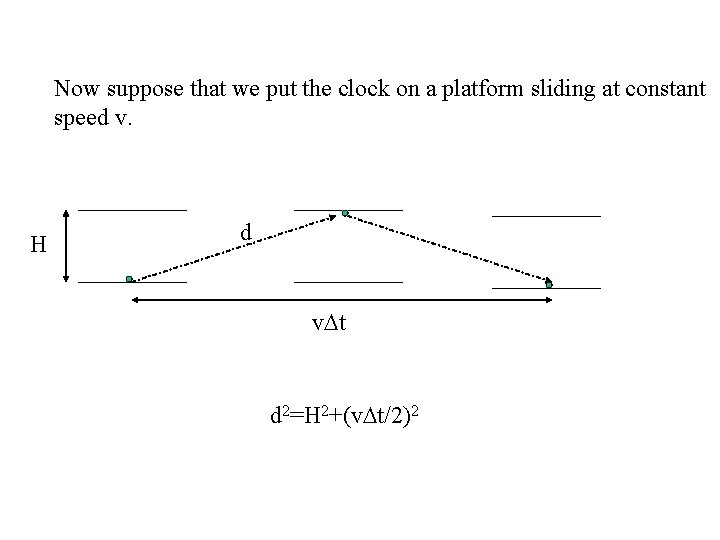
Now suppose that we put the clock on a platform sliding at constant speed v. H d v. Dt d 2=H 2+(v. Dt/2)2

• Clock appears to run more slowly. • But, suppose there’s an astronaut in the spacecraft – the inside of the spacecraft is also an inertial frame of reference – Einstein’s postulates apply… – So, the astronaut will measure a “tick” that lasts Dto=H/c • So, different observers see the clock going at different speeds! • Time is not absolute!

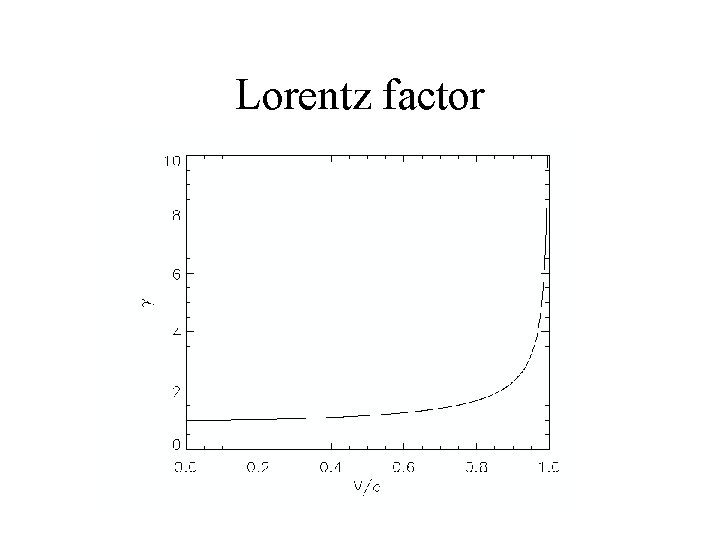
• Effect called Time Dilation. • Clock slows by a factor of • This is called the Lorentz factor, or G

Lorentz factor

Examples of time dilation [We will work through these examples on the white board during the class] • Fast moving spacecraft • The Apollo mission to the Moon • Clocks flown in airliners • Normal everyday life • The Muon Experiment • The jet in the galaxy M 87

The jet in M 87

IV: LENGTH CONTRACTION • Consider two “markers” in space. • Suppose spacecraft flies between two markers at velocity v. • Compare what would be seen by observer at rest w. r. t. markers, and an astronaut in the spacecraft…

• So, moving observers see that objects contract in the direction of motion. • Length contraction… also called – Lorentz contraction – Fitz. Gerald contraction • Consider Muon experiment again, this time from point of view of the Muons – i. e. think in frame of reference in which Muon is at rest – Decay time in this frame is 2 s (2/1000, 000 s) – How to they get from top to bottom of Mountain before decaying?

– From point of view of Muon, Mountain’s height contracts by factor of – Muons can then travel reduced distance (at almost speed of light) before decaying.

New velocity addition law • Once we’ve taken into account the way that time and distances change, what’s the new law for adding velocities?