Special Square Matrices 2 x 2 over Zp

References Used l Linear Algebra with Applications 7 E. ¡Leon, Steven. l. Discrete Mathematical

Today l Which Finite Fields l List Special Matrices l List Properties l Give

Types of Special Square Matrices l Symmetric, Skew-symmetric matrices l Orthogonal matrices l Nilpotent,

What makes a Special Square Matrix l Obviously square (2 x 2) l Types

Stochastic Matrices l Properties ¡Each row and/or column sum = 1 or =k ¡λ

Rank One Matrices l Properties ¡A = u v t ¡λ = vt u

Real Eigenvalues l Under what conditions do real eigenvalues exist l A 2*2 over

Properties l Eigenvalues Special Matrix Symmetric Skew-Symmetric Stochastic = k Orthogonal Nilpotent Idempotent Rank

How else to find them l How do we know when the discriminant is

Examples EXAMPLES: (3, 4, 5) => (j, k) = (1, 2) (5, 12, 13)

Next… l Making the connections l Moving on to Z 5, Z 7, Zp

Connections l What are the relationships between each matrix in Zp? l What are

Slides: 34

Download presentation

Special Square Matrices (2 x 2) over Zp By OC Josh Zimmer

References Used l Linear Algebra with Applications 7 E. ¡Leon, Steven. l. Discrete Mathematical Structures 5 E. ¡Kolman, Busby, Ross. l Linear Algebra with Applications 5 E. ¡Strang, Gilbert.

Today l Which Finite Fields l List Special Matrices l List Properties l Give Examples l What we are looking for l Different ways how to find it

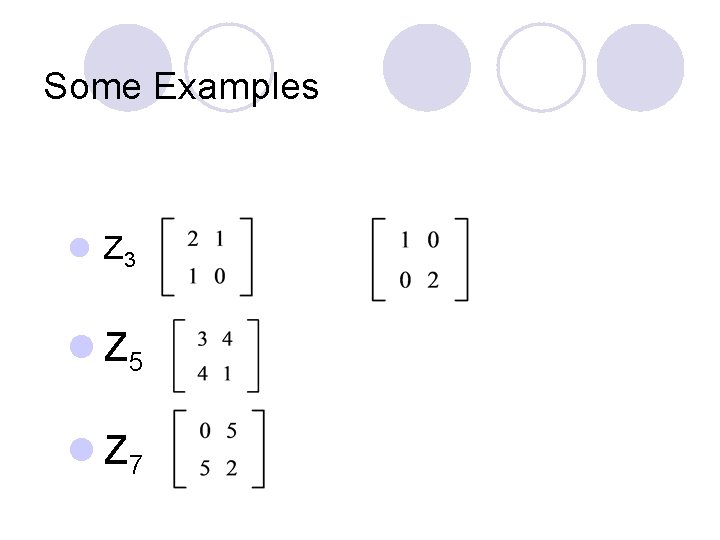
Matrices in Zp l l l Z 2 = {0, 1} Z 3 = {0, 1, 2} Z 5 = {0, 1, 2, 3, 4} Z 7 = {0, 1, 2, 3, 4, 5, 6} Zp where p is a prime number

Types of Special Square Matrices l Symmetric, Skew-symmetric matrices l Orthogonal matrices l Nilpotent, Idempotent matrices l Stochastic matrices l Rank One matrices

What makes a Special Square Matrix l Obviously square (2 x 2) l Types of special we are concerned with ¡ ¡ ¡ Symmetric, Skew-symmetric matrices Orthogonal matrices Nilpotent, Idempotent matrices Stochastic Rank One l First starting with small finite fields (Z 2) then moving higher

Symmetric Matrices

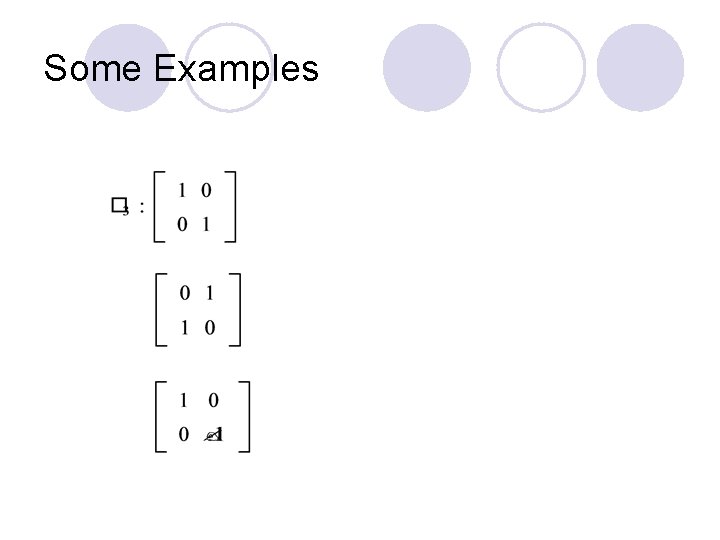
Some Examples l Z 3 l Z 5 l Z 7

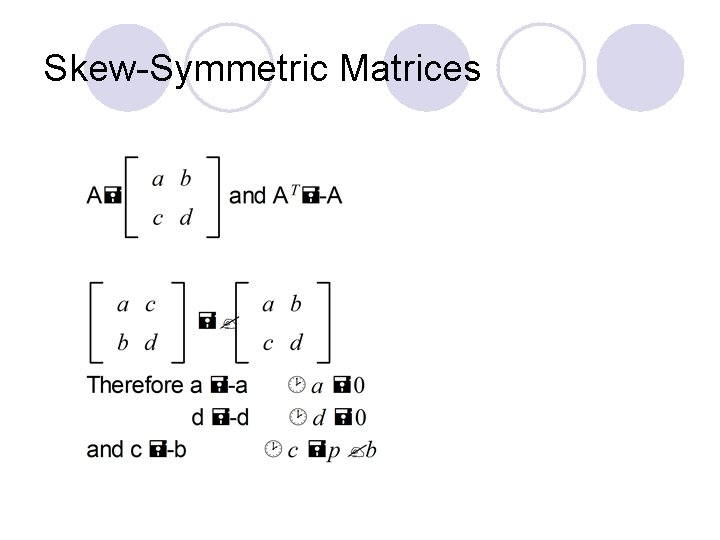
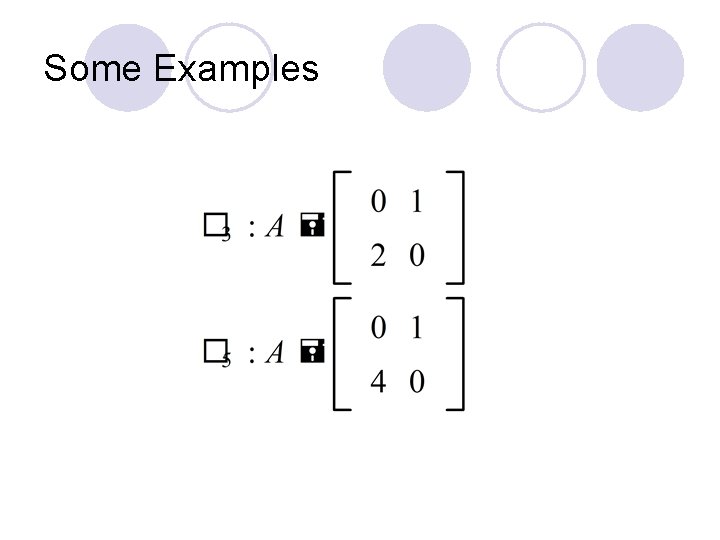
Skew-Symmetric Matrices

Some Examples

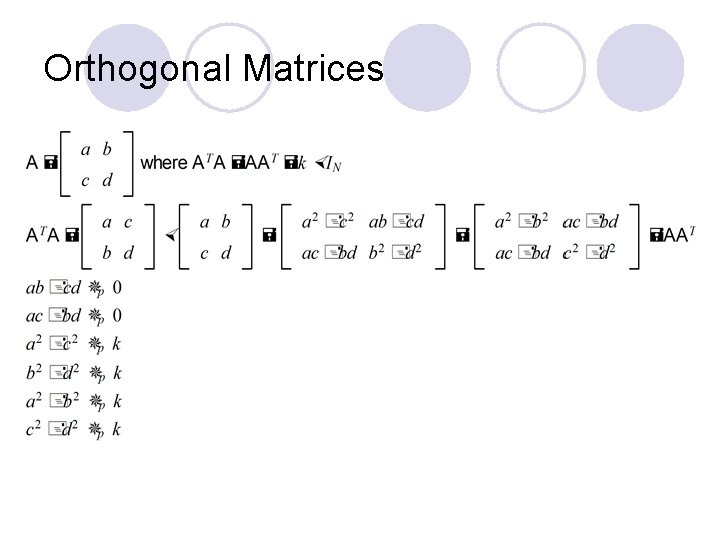
Orthogonal Matrices

Some Examples

Nilpotent Matrices

Nilpotent Matrix Examples

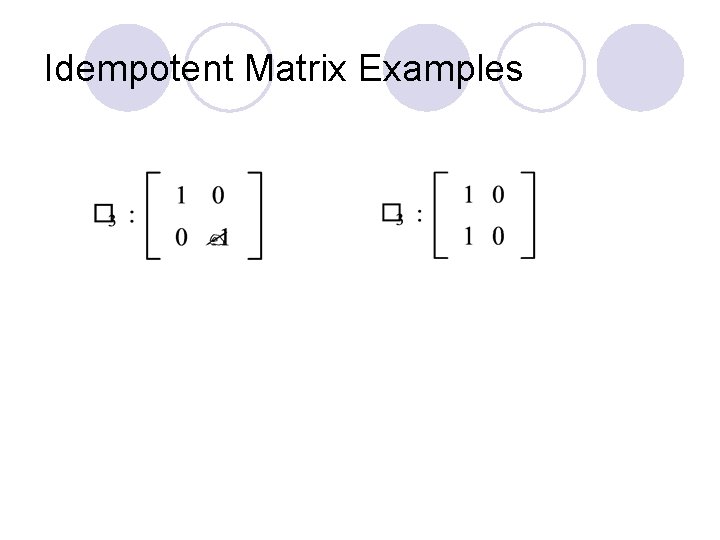
Idempotent Matrices

Idempotent Matrix Examples

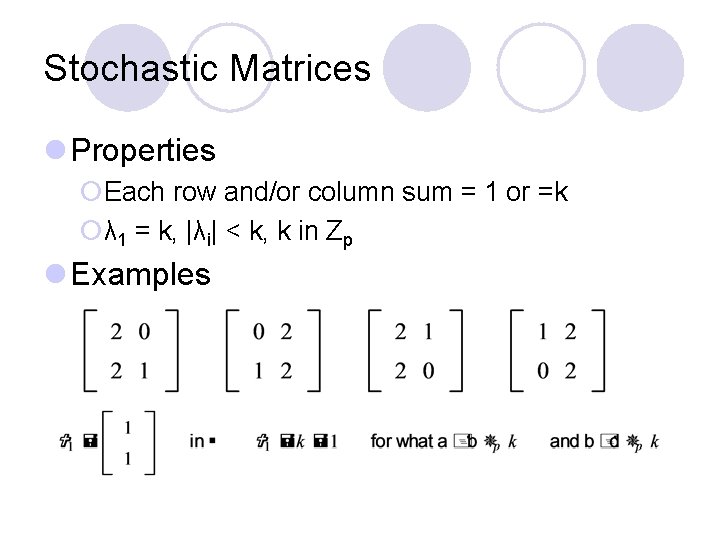
Stochastic Matrices l Properties ¡Each row and/or column sum = 1 or =k ¡λ 1 = k, |λi| < k, k in Zp l Examples

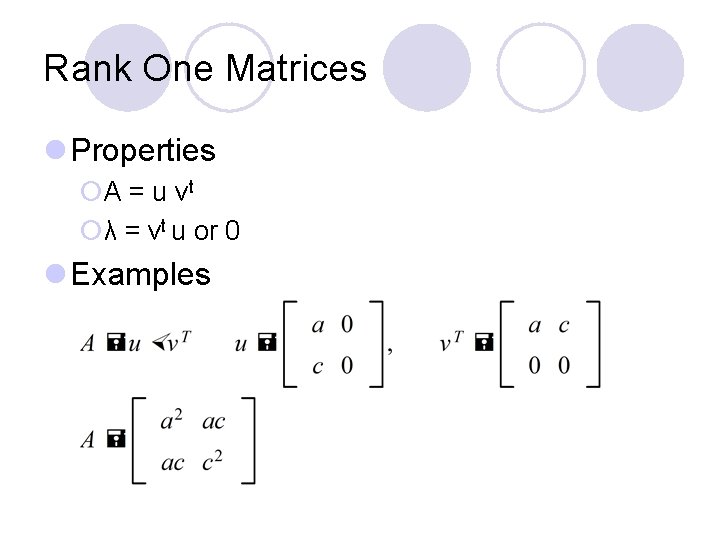
Rank One Matrices l Properties ¡A = u v t ¡λ = vt u or 0 l Examples

Real Eigenvalues l Under what conditions do real eigenvalues exist l A 2*2 over Z 2 has 16 different possible matrices l Eigenvalues of these matrices l of A 2*2 in Z 3 over Z 3 ¡ λ²-(a+d)λ+(ad-bc)=0

Ones that Exist

What to look for

How do we find these Eigenvalues?

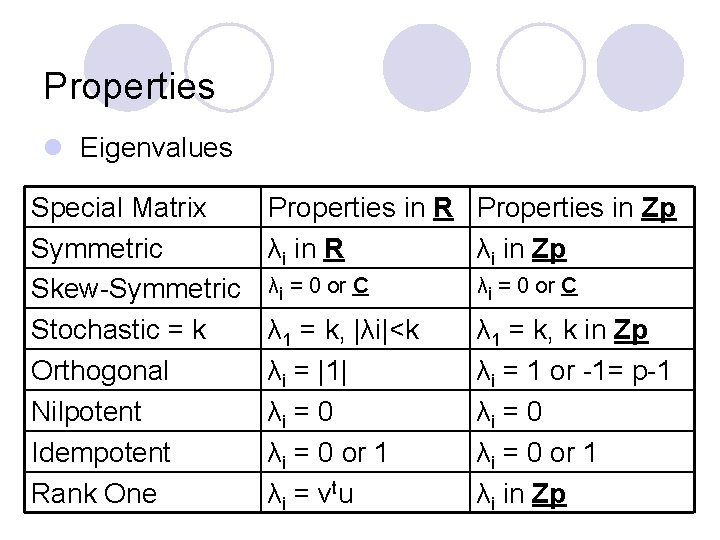
Properties l Eigenvalues Special Matrix Symmetric Skew-Symmetric Stochastic = k Orthogonal Nilpotent Idempotent Rank One Properties in R Properties in Zp λi in R λi in Zp λi = 0 or C λ 1 = k, |λi|<k λi = |1| λi = 0 or 1 λi = vtu λ 1 = k, k in Zp λi = 1 or -1= p-1 λi = 0 or 1 λi in Zp

What happens if they don’t Exist?

Limits due to field Zp

How else to find them l How do we know when the discriminant is a perfect square? l Pythagorean triples help us identify what combinations will yield a perfect square thus giving us an eigenvalue in Zp

Pythagorean Triples

Examples EXAMPLES: (3, 4, 5) => (j, k) = (1, 2) (5, 12, 13) => (j, k) = (2, 3) (8, 15, 17) => (j, k) = (1, 4)

Solve

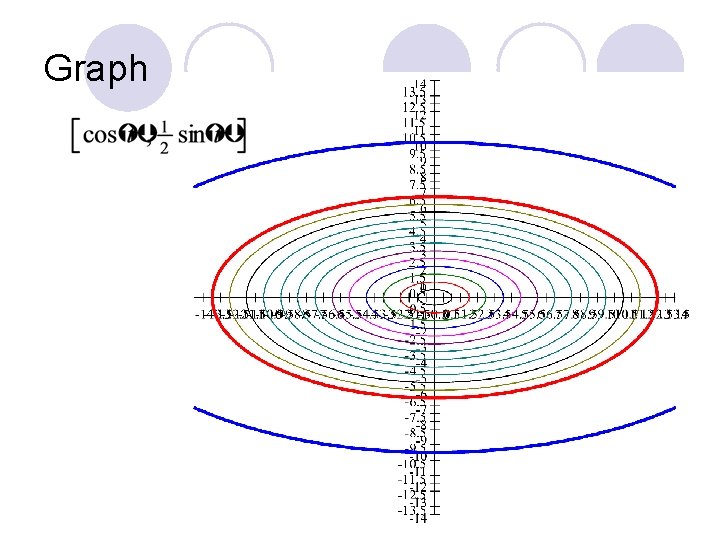
Graph

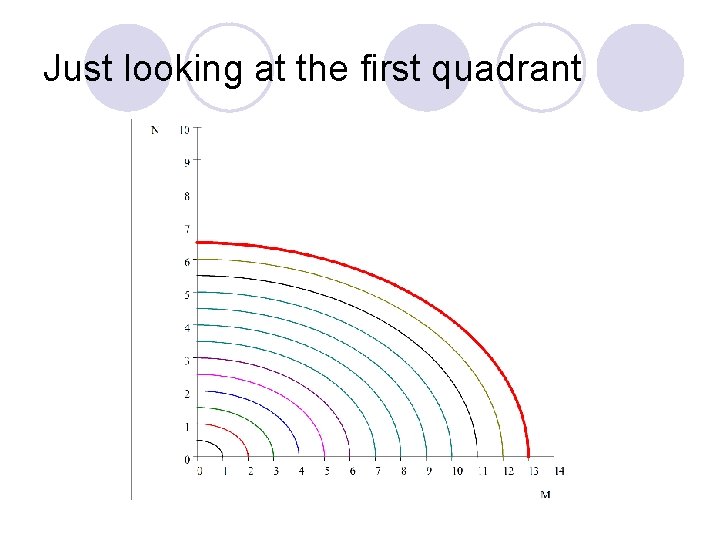
Just looking at the first quadrant

Next… l Making the connections l Moving on to Z 5, Z 7, Zp l When is the Discriminant a perfect square?

Connections l What are the relationships between each matrix in Zp? l What are the relationships between their Eigenvalues? l Are the Eigenvalues still in Zp?

Questions… l Time ≤ 25 minutes