Special Relativity 1 Albert Einstein the high school

Special Relativity 1

Albert Einstein, the high school dropout and patent office clerk published his ideas on Special Relativity in 1905. 2

Special vs. General Relativity Special Relativity deals with non-accelerated motion or uniform motion. General Relativity deals with motion in an accelerated frame of reference. 3

Motion is Relative n. A frame of reference is a place from which motion is observed and measured. – An object may have different velocities relative to different frames of reference. 4

Old Ideas n Originally, it was though that space was filled with a mysterious substance called ether. 5

First Postulate All laws of nature are the same in all uniformly moving frames of reference. 6

Second Postulate The speed of light in free space has the same measured value for all observers regardless of the motion of the source or the motion of the observer; that is, the speed of light is a constant. 7

Second Postulate A flash of light is emitted from the station. Regardless of the velocity of the rocket, an observer in the rocket sees the flash of light pass by at the same speed, c. If a flash is sent to the station from the moving rocket, observers in the station measure the speed of the flash to be c. The speed of light is measured to be the same regardless of the speed of the source or receiver! How can this be? ! 8

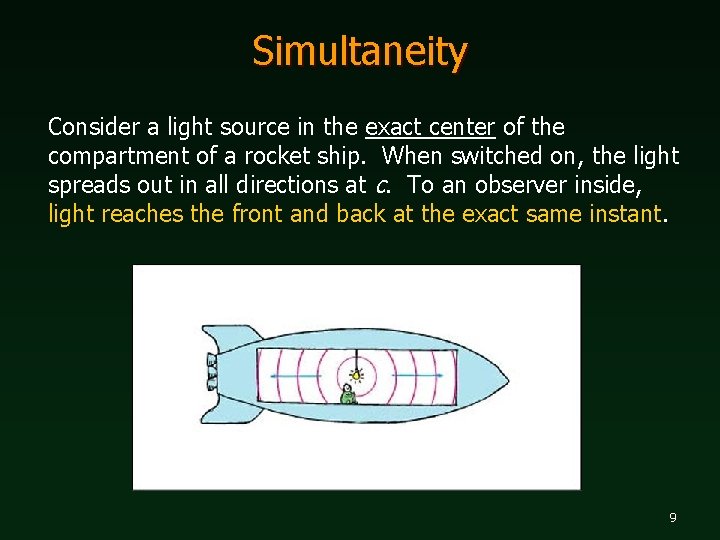
Simultaneity Consider a light source in the exact center of the compartment of a rocket ship. When switched on, the light spreads out in all directions at c. To an observer inside, light reaches the front and back at the exact same instant. 9

Simultaneity As light travels out from the source, an observer on the ground sees the ship move forward, so the back of the compartment moves toward the beam while the front moves away from it. Since the speed of light is the same in both directions, this outside observer sees the event of light hitting the back of the compartment before seeing the event of light hitting the front of the compartment. 10

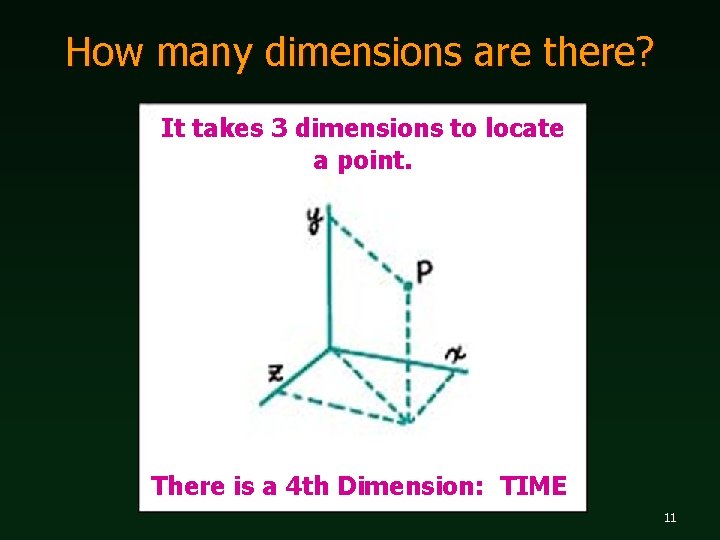
How many dimensions are there? It takes 3 dimensions to locate a point. There is a 4 th Dimension: TIME 11

Space and Time are Integrally Linked SPACETIME The ratio of space to time is a constant. The greater the measured distance in space, the greater the measured interval of time. 12

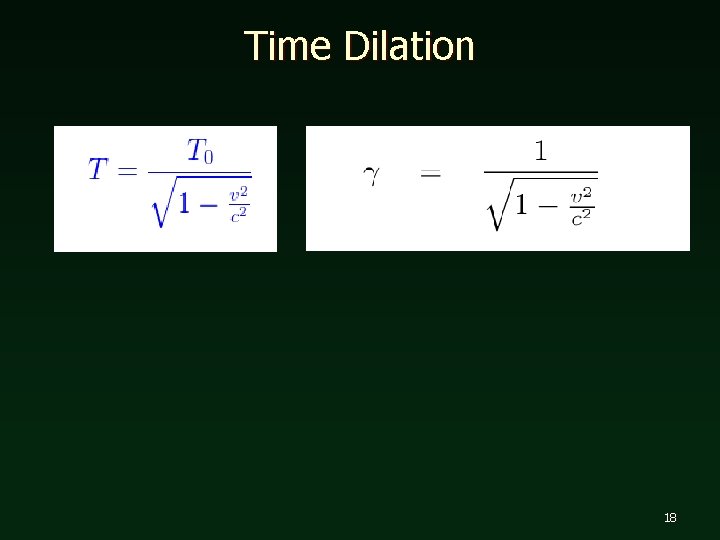
Time Dilation Because of this constant ratio of space to time, a major prediction of special relativity (confirmed by countless experiments) is that time can be stretched; this is called time dilation. 13

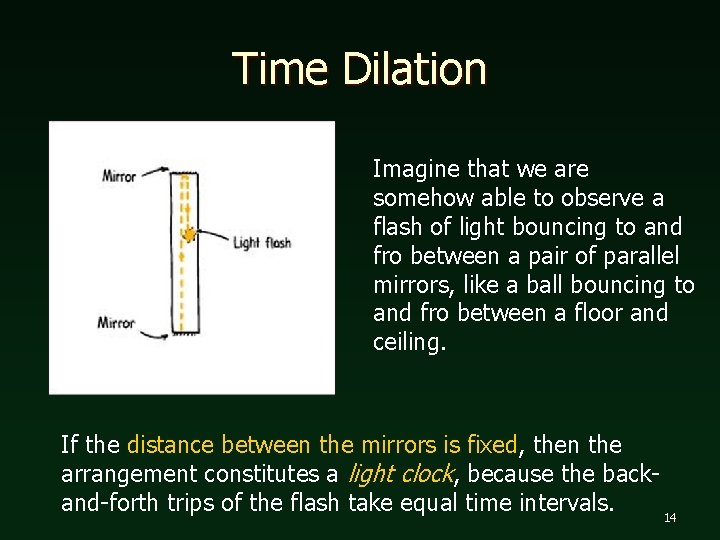
Time Dilation Imagine that we are somehow able to observe a flash of light bouncing to and fro between a pair of parallel mirrors, like a ball bouncing to and fro between a floor and ceiling. If the distance between the mirrors is fixed, then the arrangement constitutes a light clock, because the backand-forth trips of the flash take equal time intervals. 14

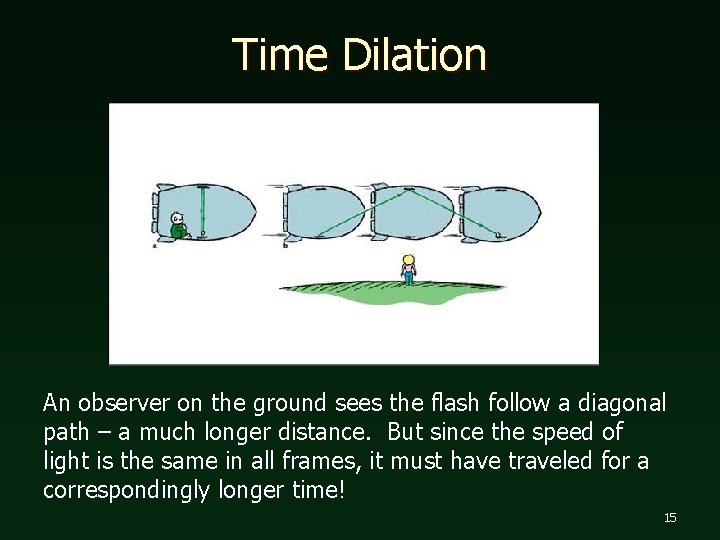
Time Dilation An observer on the ground sees the flash follow a diagonal path – a much longer distance. But since the speed of light is the same in all frames, it must have traveled for a correspondingly longer time! 15

Time Dilation All clocks run more slowly when moving than when at rest. Time dilation has to do not with the mechanics of clocks but with the nature of time itself. 16

Time Dilation 17

Time Dilation 18

Lorentz Factor as a Function of Speed 19

Twin Paradox 20

Length Contraction As objects move through spacetime, space as well as time changes. In a nutshell, space is contracted, making the objects look shorter when they move by us at relativistic speeds. 21

Length Contraction Lorentz Contraction George F. Fitz. Gerald Hendrik A. Lorentz 22

Length Contraction 23

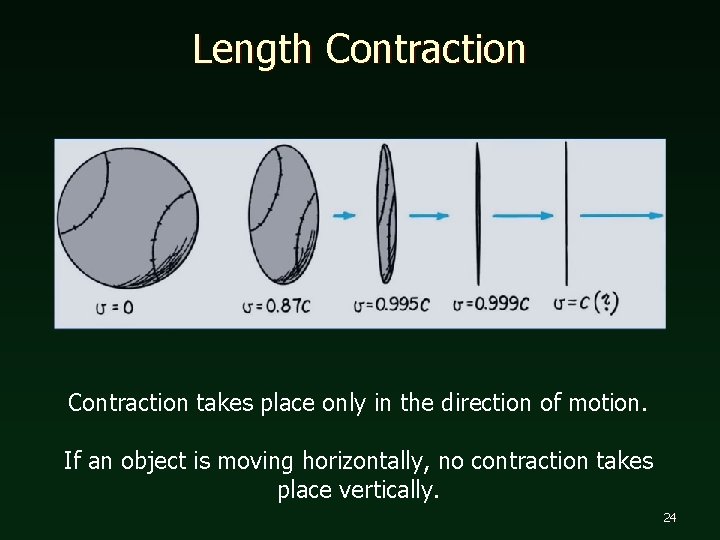
Length Contraction takes place only in the direction of motion. If an object is moving horizontally, no contraction takes place vertically. 24

Length Contraction 25

Length Contraction In Lisa’s frame of reference, her meterstick is 1 meter but the spacecraft’s meterstick is contracted. From the spacecraft’s perspective, Lisa’s meterstick is contracted! So which is ACTUALLY contracted? The answer is that it’s all relative. 26

Length Contraction 27

Length Contraction Lizzie is scooting down the Interstate at 18% the speed of light and measures the distance between mileposts to be less than 5280’. a. What is the distance that Lizzie measures between the mileposts? b. What would be the distance she measures at twice her speed? 28

Twin Paradox 29

Let’s Do a Thought Experiment n We have two ships, identical except for their color. – Same Size, Length n Ships are traveling in opposite directions, at constant and equal speeds. n First, let’s define 4 different events that we can observe from different frames of reference. 30

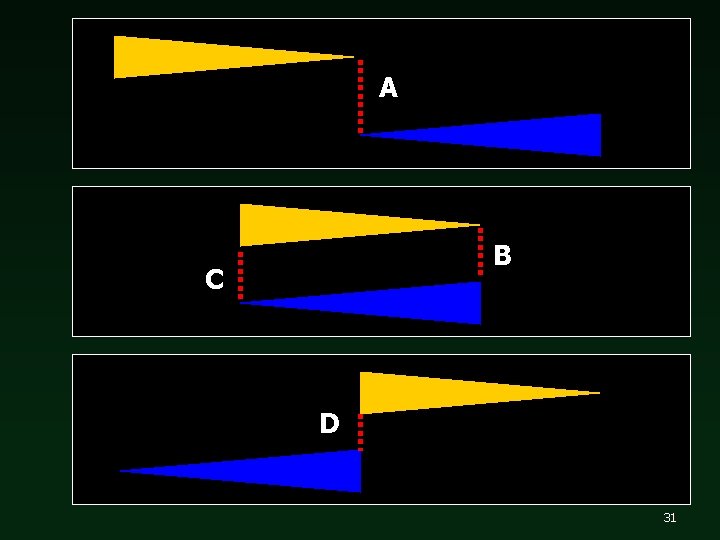
A B C D 31

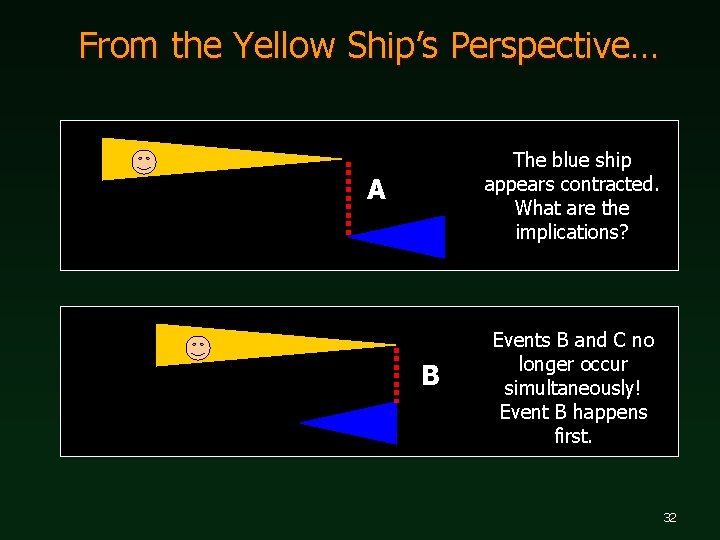
From the Yellow Ship’s Perspective… The blue ship appears contracted. What are the implications? A B Events B and C no longer occur simultaneously! Event B happens first. 32

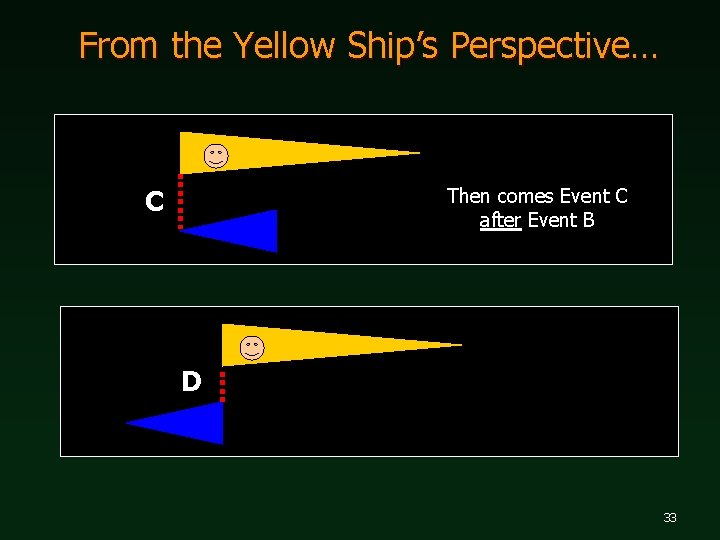
From the Yellow Ship’s Perspective… C Then comes Event C after Event B D 33

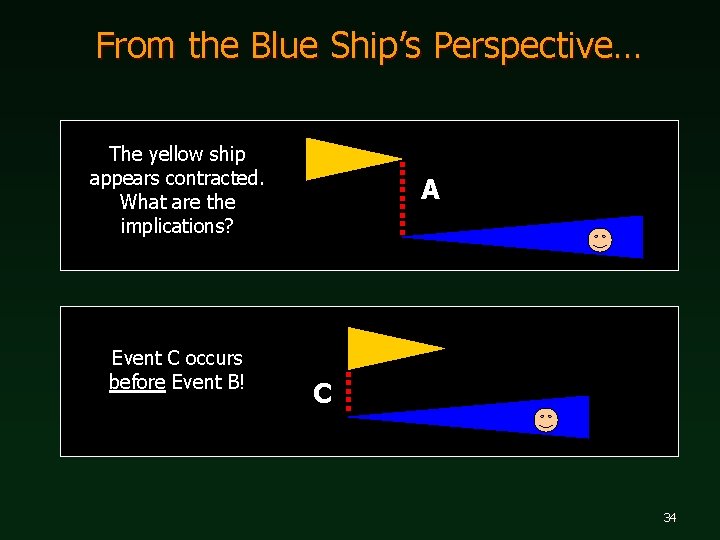
From the Blue Ship’s Perspective… The yellow ship appears contracted. What are the implications? Event C occurs before Event B! A C 34

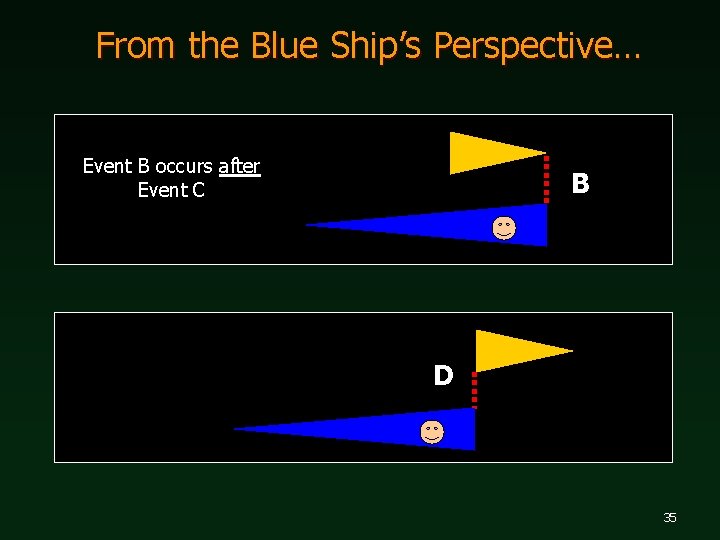
From the Blue Ship’s Perspective… Event B occurs after Event C B D 35

Relativity Breaks Simultaneity n Event order for the yellow ship - A B C D n Event order for the blue ship - A C B D n The amount of time elapsed from A to D is the same for each ship. BUT… n The amount of time from A to B is very different! 36

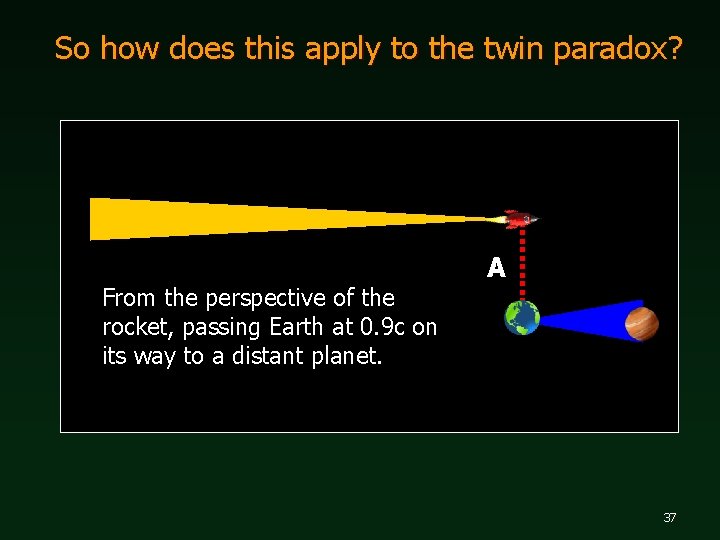
So how does this apply to the twin paradox? From the perspective of the rocket, passing Earth at 0. 9 c on its way to a distant planet. A 37

So how does this apply to the twin paradox? B Rocket went from A to B. Event C has not yet occurred. DONE! 38

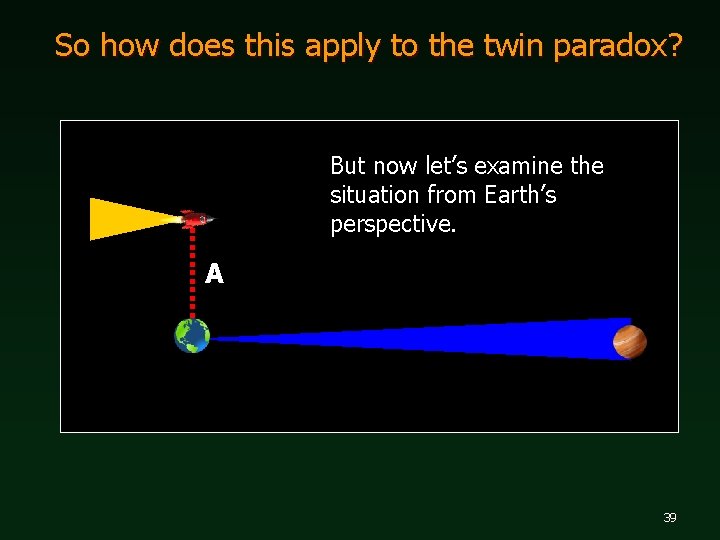
So how does this apply to the twin paradox? But now let’s examine the situation from Earth’s perspective. A 39

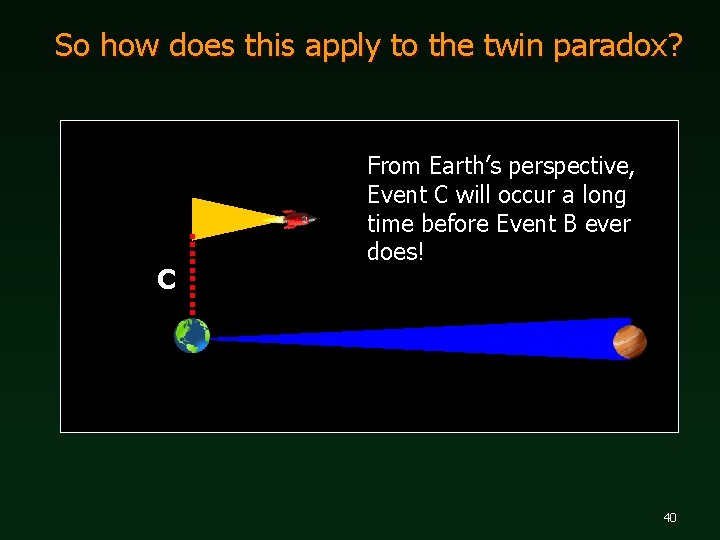
So how does this apply to the twin paradox? C From Earth’s perspective, Event C will occur a long time before Event B ever does! 40

So how does this apply to the twin paradox? Waiting… 41

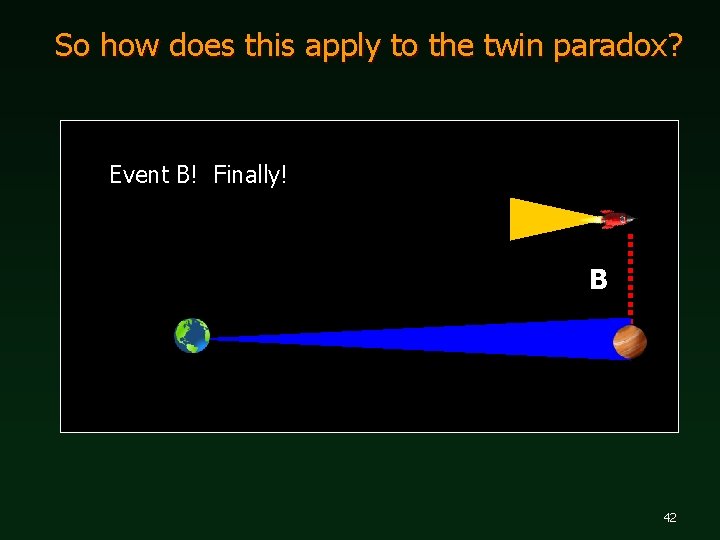
So how does this apply to the twin paradox? Event B! Finally! B 42

So how does this apply to the twin paradox? n In Earth’s reference frame, more time has elapsed from A to B. We can see that because event C happened in the interim. n But in the Rocket’s reference frame, event C has not occurred at all! The time from A to B was shorter. n So the twin on Earth has aged much more than the twin in the Rocket. When they meet up again in the same reference frame, more time has elapsed for one than the other! 43

Relativistic Velocities 44

Relativistic Velocities 45

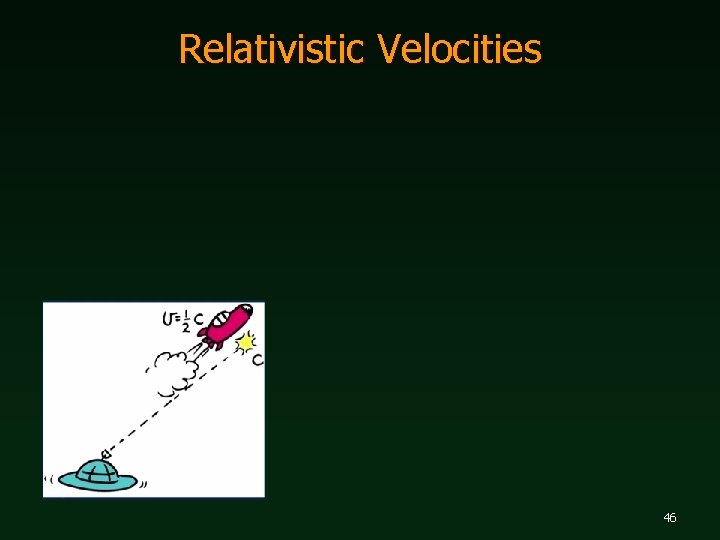
Relativistic Velocities 46

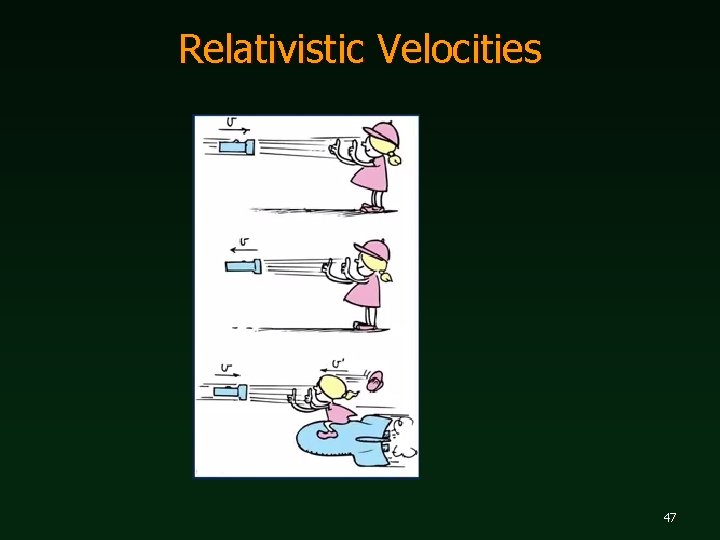
Relativistic Velocities 47

Relativistic Velocities 48

Relativistic Momentum The Stanford Linear Accelerator 49

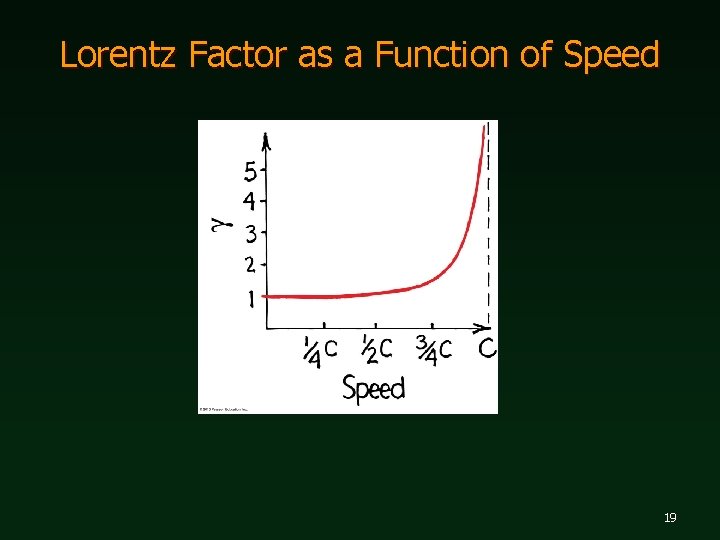
Relativistic Momentum At everyday speeds, γ is approximately 1 and so we don’t notice the effects of relativity. As speed approaches c though, γ approaches infinity. No matter how close to c an object is pushed, it would still require infinite impulse to give it the last bit of speed needed to reach c – clearly impossible. No body with mass can be pushed to the speed of light, much less beyond it. 50

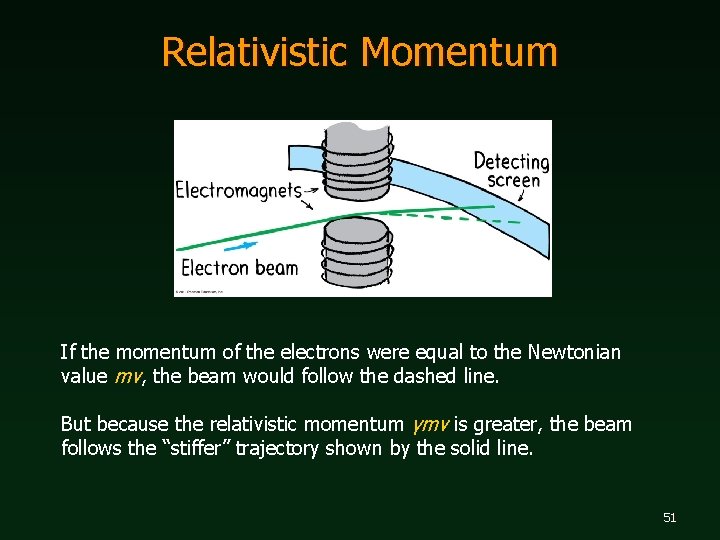
Relativistic Momentum If the momentum of the electrons were equal to the Newtonian value mv, the beam would follow the dashed line. But because the relativistic momentum γmv is greater, the beam follows the “stiffer” trajectory shown by the solid line. 51

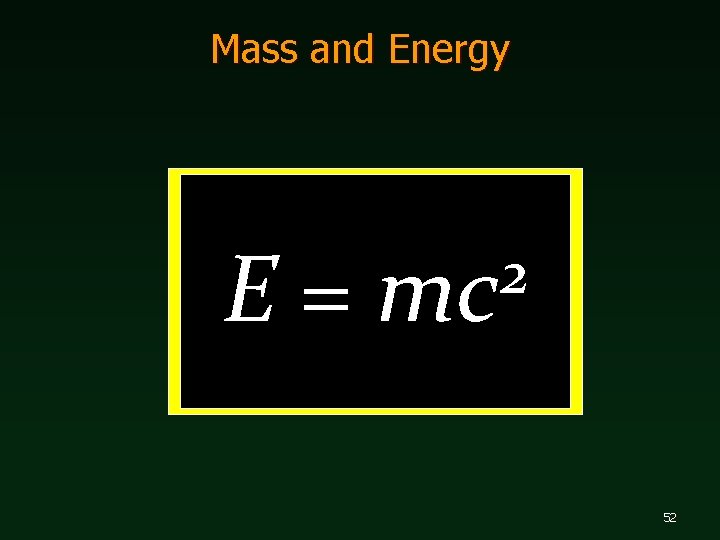
Mass and Energy E= 2 mc 52

Mass and Energy 53

The Correspondence Principle 54

Thomas, a rhino, is 2. 5 meters long when at rest. How long will you measure him to be when he runs past you at 0. 80 c? How much time will you say it takes for him to pass you? 55

56