Special Products Square of a Binomial Prepared By

Special Products: Square of a Binomial Prepared By: Mr. Albert F. Perez June 29, 2015

Review Write the letter of the product in column II that matches with each item in column I. Column I T 1. (3 x) (4 x 2) ___ I 2. (5 x 3)(7 x 4) ___ M 3. x(3 x 4 + 2 x) ___ E 4. (x + 7)(x – 6) ___ S 5. (2 x + 1)(3 x + 8) ___ Column II E. x 2 +x – 42 I. 35 x 7 M. 3 x 5 + 2 x 2 N. 6 x 2 + 8 S. 6 x 2 + 19 x + 8 T. 12 x 3
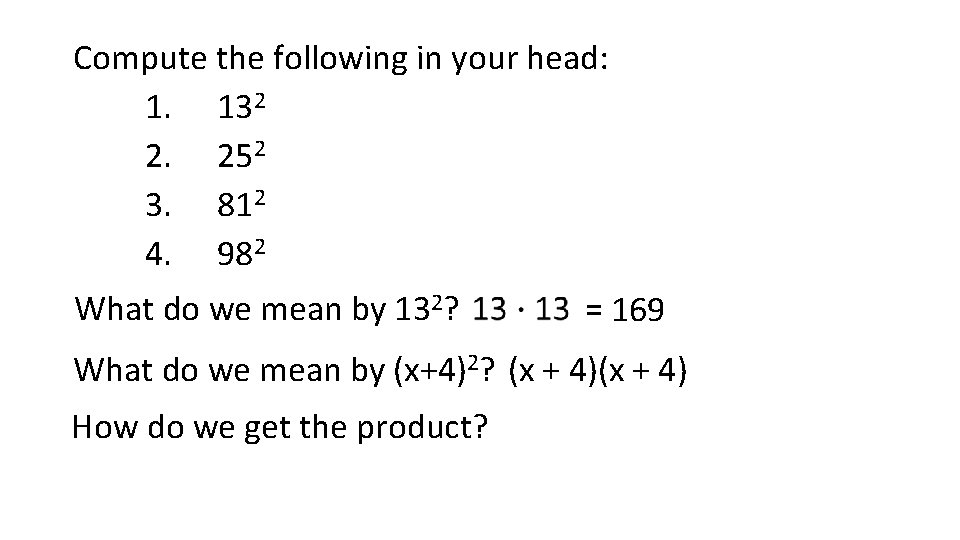
Compute the following in your head: 1. 132 2. 252 3. 812 4. 982 What do we mean by 132? = 169 What do we mean by (x+4)2? (x + 4) How do we get the product?
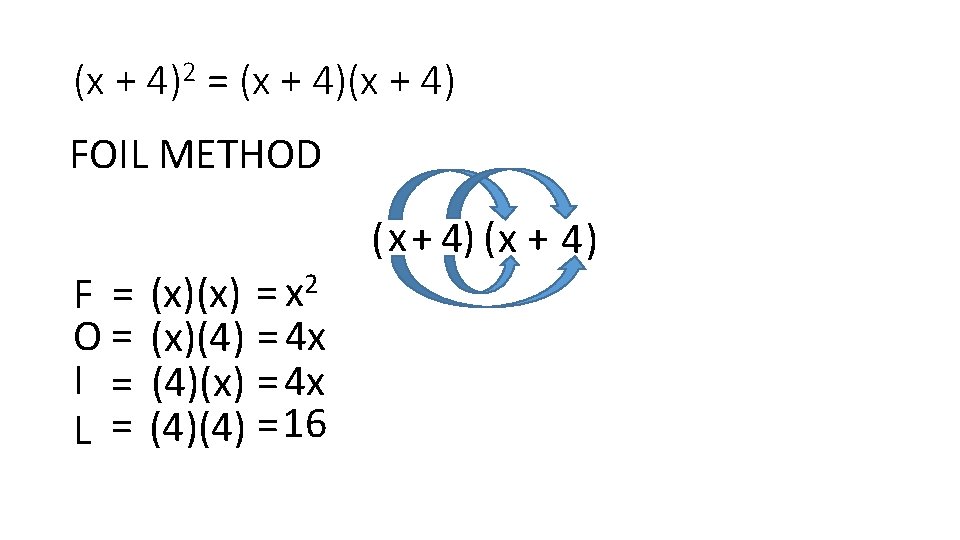
(x + 4)2 = (x + 4) FOIL METHOD F = O= I = L = (x)(x) = x 2 (x)(4) = 4 x (4)(x) = 4 x (4)(4) = 16 ( x + 4)
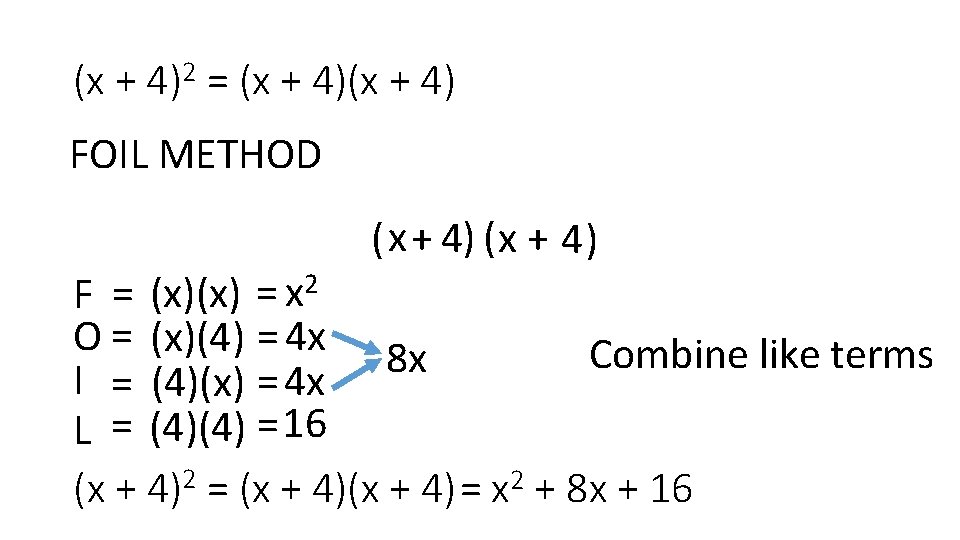
(x + 4)2 = (x + 4) FOIL METHOD ( x + 4) F = (x)(x) = x 2 O = (x)(4) = 4 x 8 x Combine like terms I = (4)(x) = 4 x L = (4)(4) = 16 (x + 4)2 = (x + 4)= x 2 + 8 x + 16
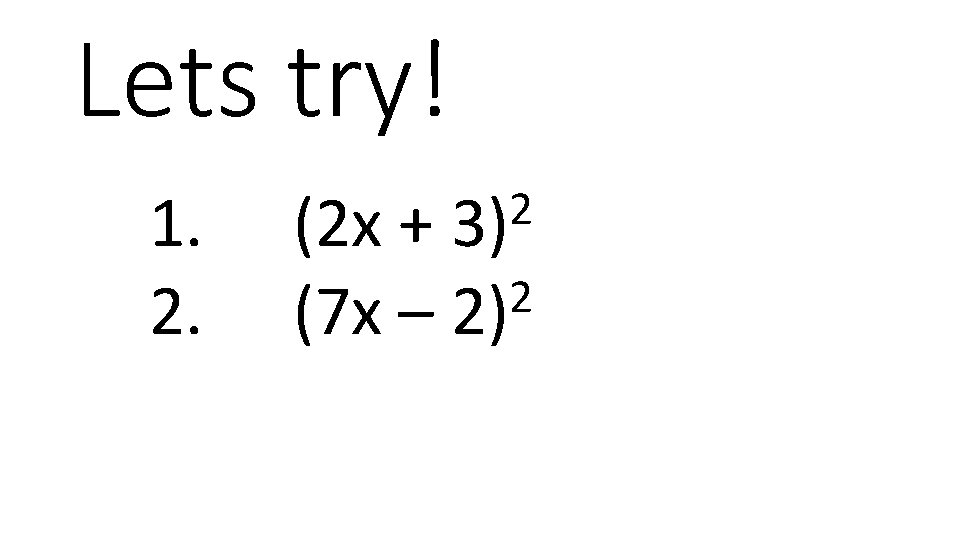
Lets try! 1. 2. 2 3) (2 x + 2 (7 x – 2)
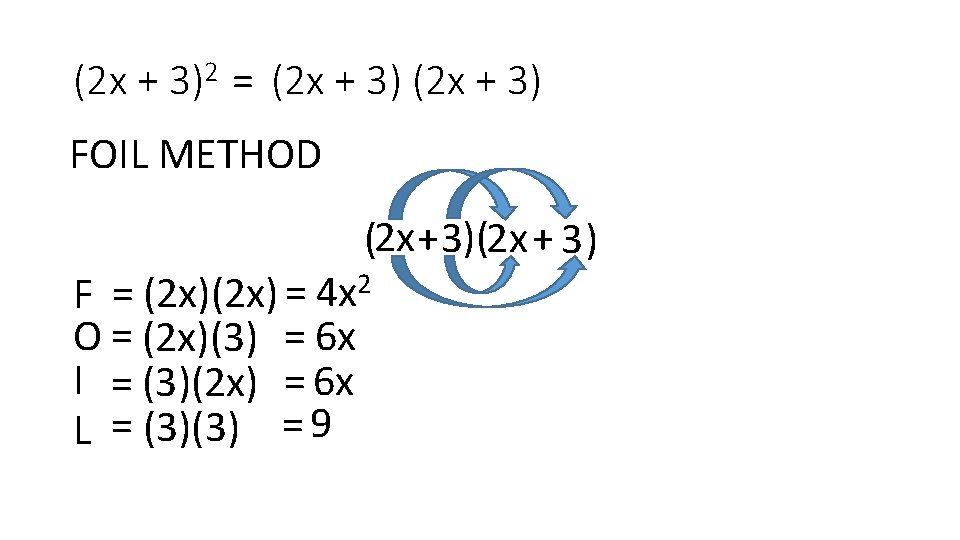
(2 x + 3)2 = (2 x + 3) FOIL METHOD (2 x +3)(2 x + 3) F = (2 x) = 4 x 2 O = (2 x)(3) = 6 x I = (3)(2 x) = 6 x L = (3)(3) = 9
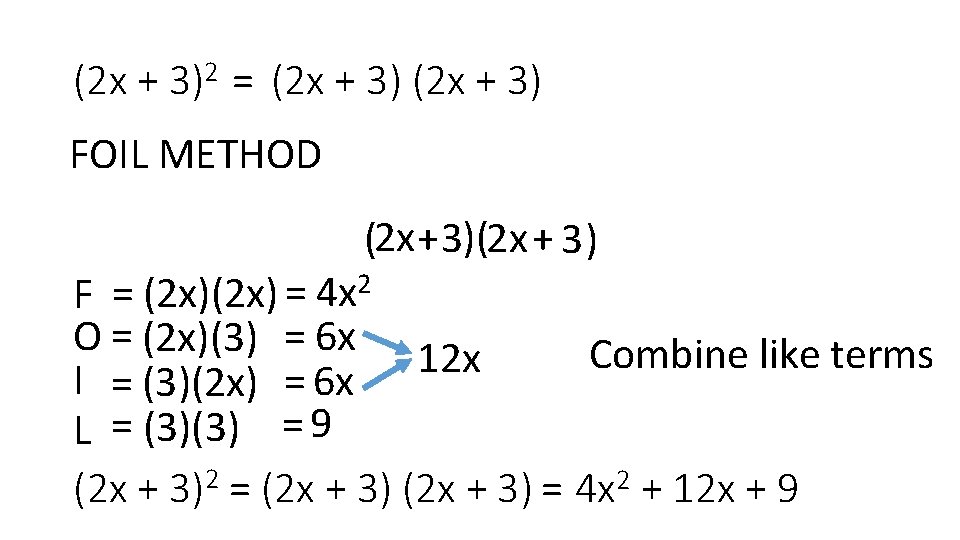
(2 x + 3)2 = (2 x + 3) FOIL METHOD (2 x +3)(2 x + 3) F = (2 x) = 4 x 2 O = (2 x)(3) = 6 x 12 x Combine like terms I = (3)(2 x) = 6 x L = (3)(3) = 9 (2 x + 3)2 = (2 x + 3) = 4 x 2 + 12 x + 9
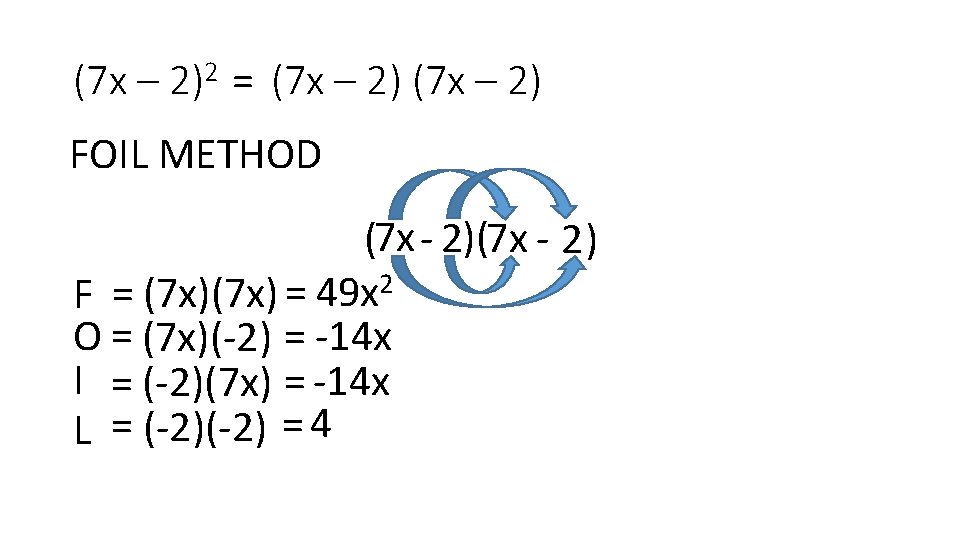
(7 x – 2)2 = (7 x – 2) FOIL METHOD (7 x - 2) F = (7 x) = 49 x 2 O = (7 x)(-2) = -14 x I = (-2)(7 x) = -14 x L = (-2) = 4
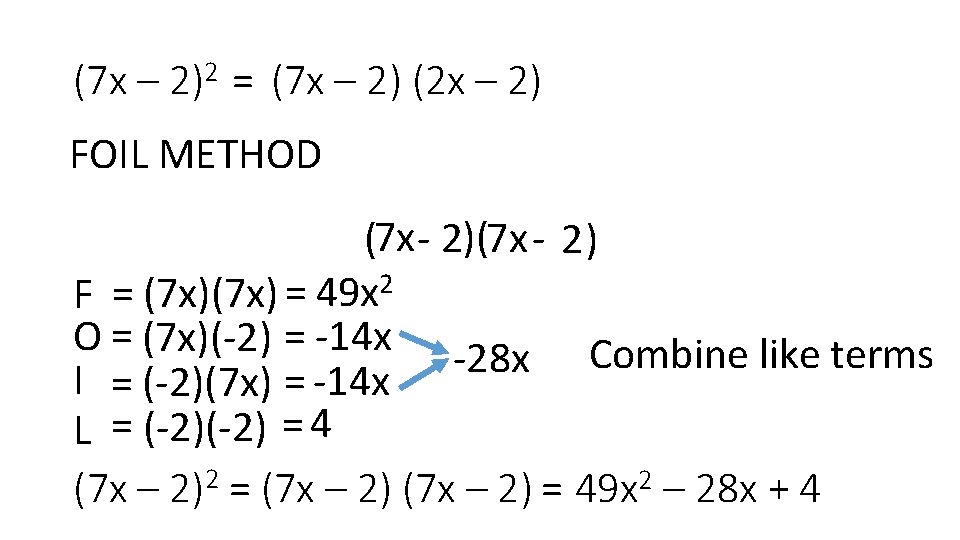
(7 x – 2)2 = (7 x – 2) (2 x – 2) FOIL METHOD (7 x - 2) F = (7 x) = 49 x 2 O = (7 x)(-2) = -14 x -28 x Combine like terms I = (-2)(7 x) = -14 x L = (-2) = 4 (7 x – 2)2 = (7 x – 2) = 49 x 2 – 28 x + 4

To square a Binomial 1. The first term of the product is the square of the first term of the binomial. 2. The middle term of the product is twice the product of the two terms of the binomial. 3. The last term of the product is the square of the last term of the binomial. (a + b)2 = a 2 + 2 ab + b 2
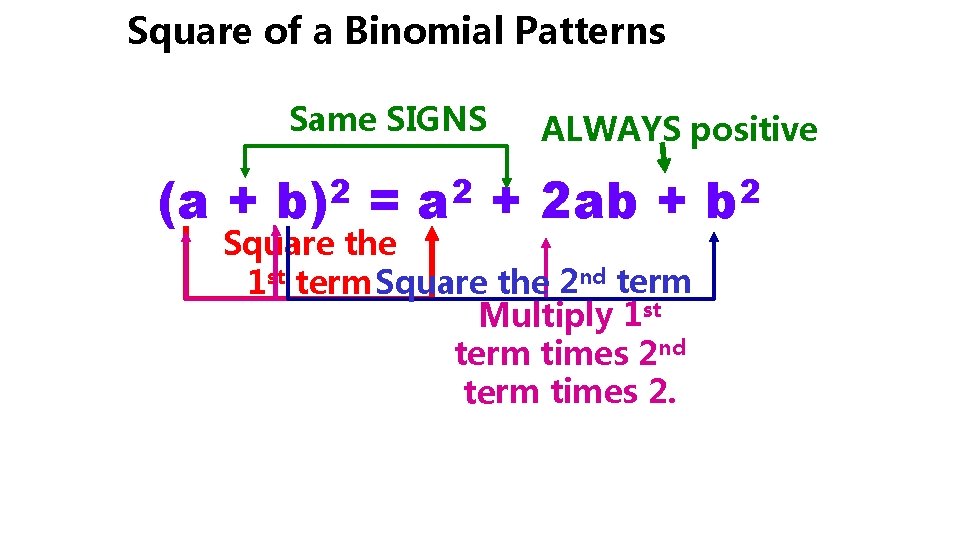
Square of a Binomial Patterns Same SIGNS (a + 2 b) = 2 a ALWAYS positive + 2 ab + Square the 1 st term Square the 2 nd term Multiply 1 st term times 2 nd term times 2. 2 b
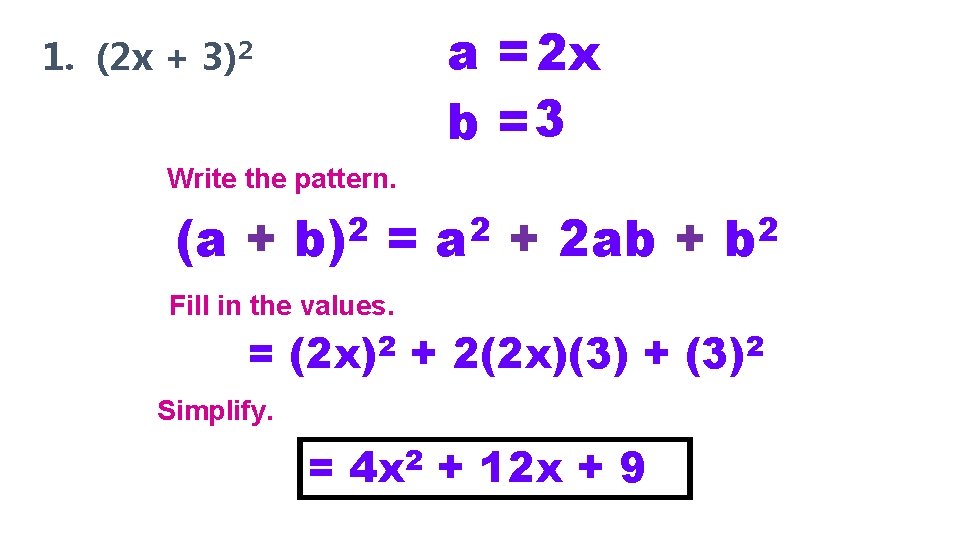
a = 2 x b =3 1. (2 x + 3)2 Write the pattern. (a + 2 b) = Fill in the values. 2 = (2 x) 2 a + 2 ab + + 2(2 x)(3) + Simplify. = 4 x 2 + 12 x + 9 2 b 2 (3)
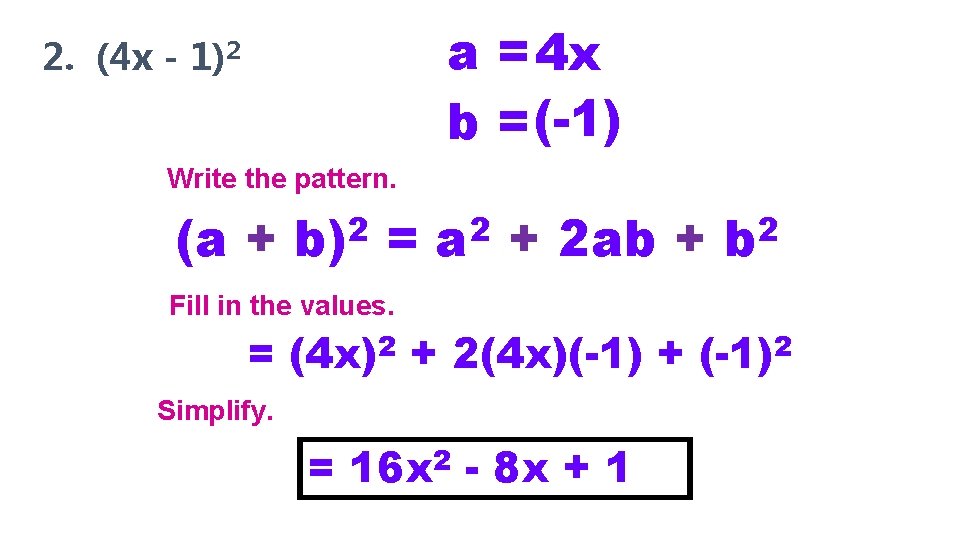
a = 4 x b = (-1) 2. (4 x - 1)2 Write the pattern. (a + 2 b) = Fill in the values. 2 = (4 x) 2 a + 2 ab + + 2(4 x)(-1) + Simplify. = 16 x 2 - 8 x + 1 2 b 2 (-1)
- Slides: 14