Spearmans rank difference method OR Spearmans Coefficient of

I. If Ranks are given Steps : (1) The two series will be given

I. If Ranks are given Spearman’s rank difference method Solution : Entries Rank by

I. If Ranks are given Formula : rk = = 6Σd 2 _______ 1

II. If Ranks are not given Example : Given below is the percentage of

II. If Ranks are not given Solution : Marks in R 1 Eco. (X)

II. Problem of Equal Ranks In such case , average rank is assigned to

II. Problem of Equal Ranks Example (1) : Calculate rank coefficient of correlation from

II. Problem of Equal Ranks Solution 1 : X R 1 Y R 2

II. Problem of Equal Ranks rk = 1 _ w rk = 1 _

II. Problem of Equal Ranks Example (2) : Calculate the rank coefficient of correlation

II. Problem of Equal Ranks Solution : 2 : X R 1 Y R

Slides: 14

Download presentation

Spearman’s rank difference method OR Spearman’s Coefficient of Correlation This method of calculating correlation was developed by Charles Edward Spearman in 1904. It is highly useful when the data predominates in qualitative phenomenon such as beauty, , honesty, leadership ability etc. This method is useful where the numerical measurement is not possible. Examples : Intelligency, Beauty, morality, etc. In this situation –data are put like –first, second, third, fourth-rank –in this way- the coefficient of correlation by Rank difference method can be found out – Two situations – (1) If Ranks are given – (2) If Ranks are not given -

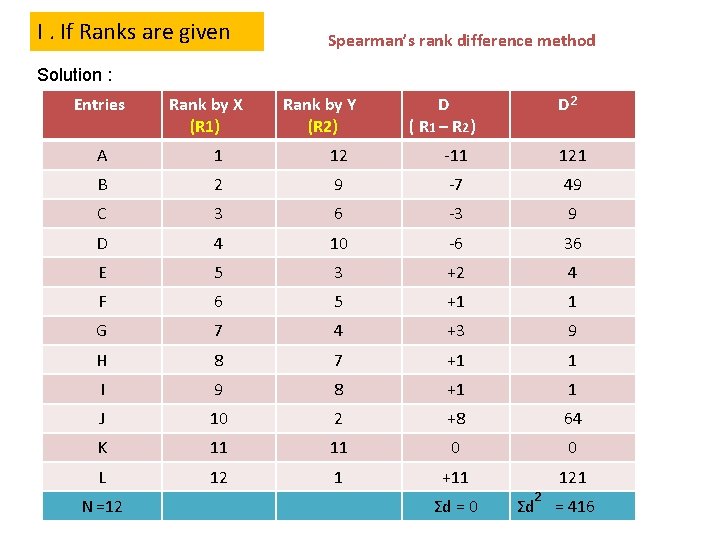
I. If Ranks are given Steps : (1) The two series will be given the name R 1 & R 2 (2) Difference between the two i. e. R 1 - R 2 obtained & expressed as – D (3) D is Squared and Σd 2 is obtained. (4) The following formula will be used – rk 6Σd 2 _______ 1 3 N - N = Example : There are two Judges in a baby competition rank the 12 entries as follows: Entries (12 students) A B C D E F G H I J K L X Judge 1 2 3 4 5 6 7 8 9 10 11 12 Y Judge 12 9 6 10 3 5 4 7 8 2 11 1

I. If Ranks are given Spearman’s rank difference method Solution : Entries Rank by X (R 1) Rank by Y (R 2) D ( R 1 – R 2) D 2 A 1 12 -11 121 B 2 9 -7 49 C 3 6 -3 9 D 4 10 -6 36 E 5 3 +2 4 F 6 5 +1 1 G 7 4 +3 9 H 8 7 +1 1 I 9 8 +1 1 J 10 2 +8 64 K 11 11 0 0 L 12 1 +11 121 N =12 Σd = 0 Σd 2 = 416

I. If Ranks are given Formula : rk = = 6Σd 2 _______ 1 3 N - N 6 x 416 1 - ____ 3 12 - 12 2496 = 1 - ______ 1716 = 1 - 1. 45 = - 0. 45 Ans. 4 slides 4

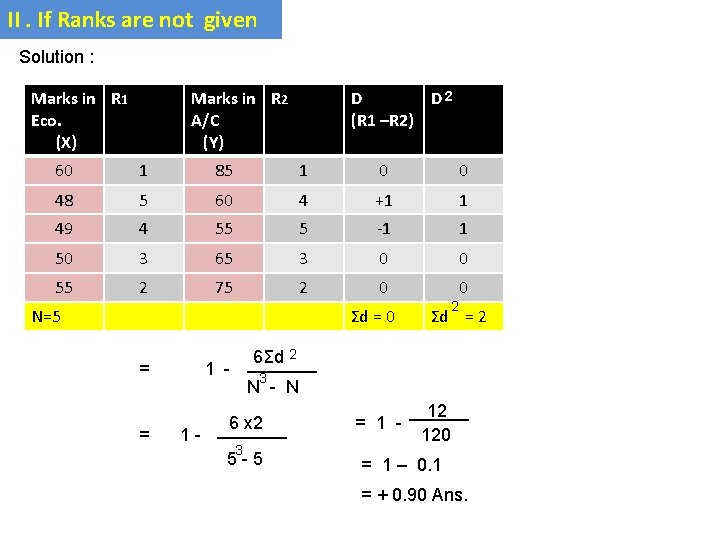
II. If Ranks are not given Example : Given below is the percentage of marks secured by 5 students in Economics and Accountancy. Students A B C D E Marks In Eco. 60 48 49 50 55 Marks In A/C 85 60 55 65 75 Calculate the coefficient of Rank Correlation

II. If Ranks are not given Solution : Marks in R 1 Eco. (X) Marks in R 2 A/C (Y) D D 2 (R 1 –R 2) 60 1 85 1 0 0 48 5 60 4 +1 1 49 4 55 5 -1 1 50 3 65 3 0 0 55 2 75 2 0 0 N=5 Σd = 0 = = 2 Σd = 2 6Σd 2 _______ 1 3 N - N 6 x 2 1 - _______ 3 5 -5 = 1 - ______ 12 120 = 1 – 0. 1 = + 0. 90 Ans.

II. Problem of Equal Ranks In such case , average rank is assigned to the similar items. For example – While granting 3 rd Rank- we find that two items have the similar value. Both of them will be accorded average rank i. e. 3+4/ 2 = 3. 5 rank If three items are then – 3+4+5/ 3 = 4 & then likewise ----In case of equal ranks are allotted to some of the entries an adjustment in the formula is made by adding 1/12(m 3 – m) M= No. of times a rank repeats itself w Formula : 1 (m 3 _ m) ] 6 [ D 2 + 12 1 _ (N 3 _ N)

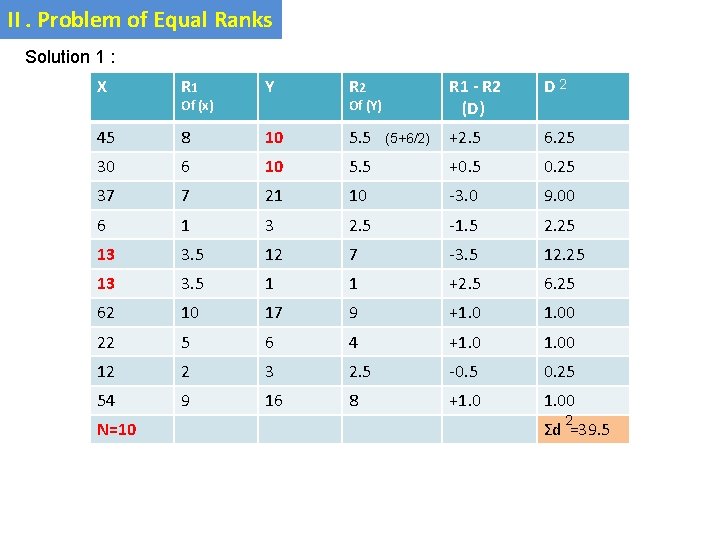
II. Problem of Equal Ranks Example (1) : Calculate rank coefficient of correlation from the following data : X : 45 30 37 6 Y : 10 10 21 3 13 13 62 22 12 54 12 1 17 6 3 16

II. Problem of Equal Ranks Solution 1 : X R 1 Y R 2 R 1 - R 2 (D) D 2 45 8 10 5. 5 +2. 5 6. 25 30 6 10 5. 5 +0. 5 0. 25 37 7 21 10 -3. 0 9. 00 6 1 3 2. 5 -1. 5 2. 25 13 3. 5 12 7 -3. 5 12. 25 13 3. 5 1 1 +2. 5 6. 25 62 10 17 9 +1. 00 22 5 6 4 +1. 00 12 2 3 2. 5 -0. 5 0. 25 54 9 16 8 +1. 00 N=10 Of (x) Of (Y) (5+6/2) 2 Σd =39. 5

II. Problem of Equal Ranks rk = 1 _ w rk = 1 _ 1 (m 3 _ m) 6 [ D 2 + 12 (N 3 _ 6 N) 1 (2 3 _ 2 ) 39. 5 + 12 (103 _ 1 (m 3 _ m) + + 12 + 1 12 (2 3 _ 2 ) + 10) + 1. 5 = 1 - 6 39. 5 _____ 990 6 x 41. 0 = 1 - _______ 990 =1 - _____ 246 990 = 1 – 0. 25 rk = 0. 75 High degree of positive correlation 1 (m 3 _ m) ] 12 1 12 (2 3 _ 2 )

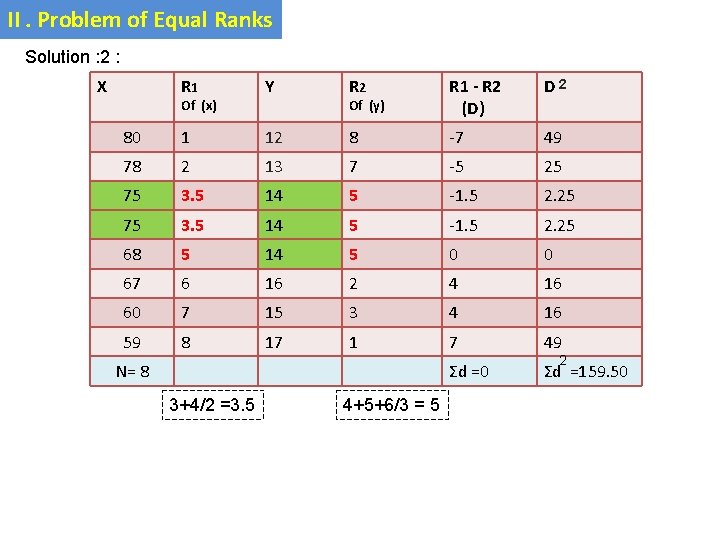
II. Problem of Equal Ranks Example (2) : Calculate the rank coefficient of correlation from the following data : X: 80 78 75 75 68 67 60 59 Y: 12 13 14 14 14 16 15 17

II. Problem of Equal Ranks Solution : 2 : X R 1 Y R 2 Of (y) R 1 - R 2 (D) D 2 80 1 12 8 -7 49 78 2 13 7 -5 25 75 3. 5 14 5 -1. 5 2. 25 68 5 14 5 0 0 67 6 16 2 4 16 60 7 15 3 4 16 59 8 17 1 7 49 Σd =0 Σd =159. 50 Of (x) N= 8 3+4/2 =3. 5 4+5+6/3 = 5 2

II. Problem of Equal Ranks rk = 1 _ w rk = 1 _ 1 (m 3 _ m) 6 [ D 2 + 12 (N 3 _ N) 6 159. 5+ 1 (2 3 _ 2 ) 12 (8 3 _ 1 (m 3 _ m) ] + 12 + 1 12 (3 3 _ 3 ) 8) + 0. 5 + 2 = 1 - 6 159. 5 ______ 504 6 x 162 = 1 - _______ 504 =1 - ____ 972 504 = 1 – 1. 93 rk = - 0. 93 High degree of Negative correlation between X & Y series

a h T k n Y u o