Spatial Statistics Point Patterns Spatial Statistics Increasing sophistication

Spatial Statistics Point Patterns

Spatial Statistics • Increasing sophistication of GIS allows archaeologists to apply a variety of spatial statistics to their data – Predictive Modeling – Intra-site Spatial Analysis

Predictive Modeling 1 • Goal is to predict where sites will be located • Usually involves two samples: known sites, surveyed areas where sites have not been found • For each group, we collect data: slope, aspect, distance to water, soil, vegetation zone, etc

Predictive Modeling 2 • Must convert nominal scales to dichotomies or an interval scale of some kind • Analysis by logistic regression or discriminant functions • For new areas we compute the probability that a site will be found

Predictive Modeling 3 • Problems: – Usually purely inductive – Goal is management not anthropology – Independent variables are those gathered for other reasons

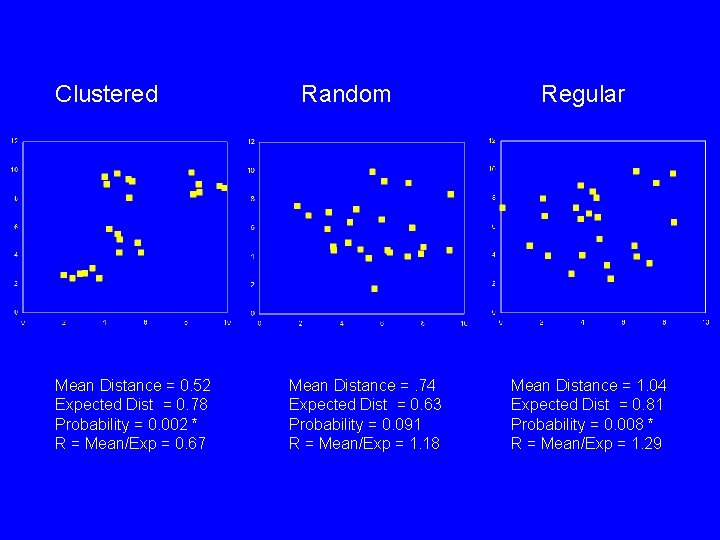
Intra-Site Spatial Analyses • Nearest Neighbor – Can use on any point plot data (sites, houses, artifacts) – Find distance to nearest neighbor for each item – Mean nearest neighbor compared to expected value (random distribution)

Nearest Neighbor • If observed mean distance is significantly less than expected, the points are clustered • If the mean distance is significantly more than expected, the points are evenly spread • But problems with borders

Clustered Mean Distance = 0. 52 Expected Dist = 0. 78 Probability = 0. 002 * R = Mean/Exp = 0. 67 Random Mean Distance =. 74 Expected Dist = 0. 63 Probability = 0. 091 R = Mean/Exp = 1. 18 Regular Mean Distance = 1. 04 Expected Dist = 0. 81 Probability = 0. 008 * R = Mean/Exp = 1. 29

Point Patterns in R • Package spatstat • Create a ppp object (point process) • Plotting and analytical tools are extensive

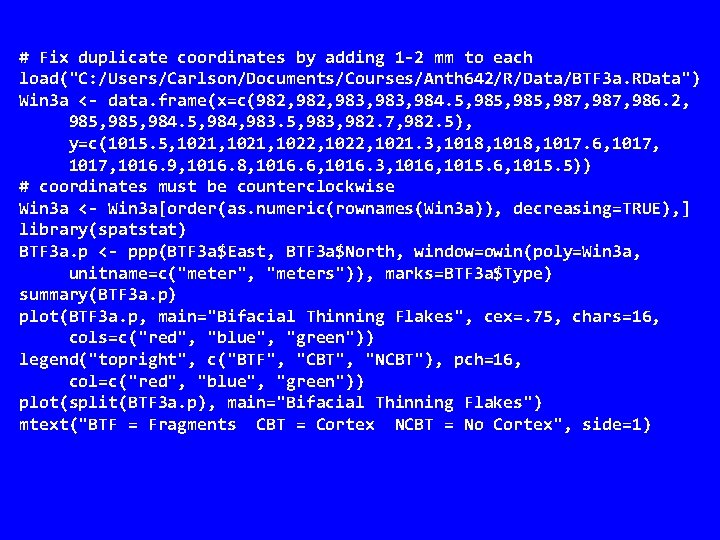
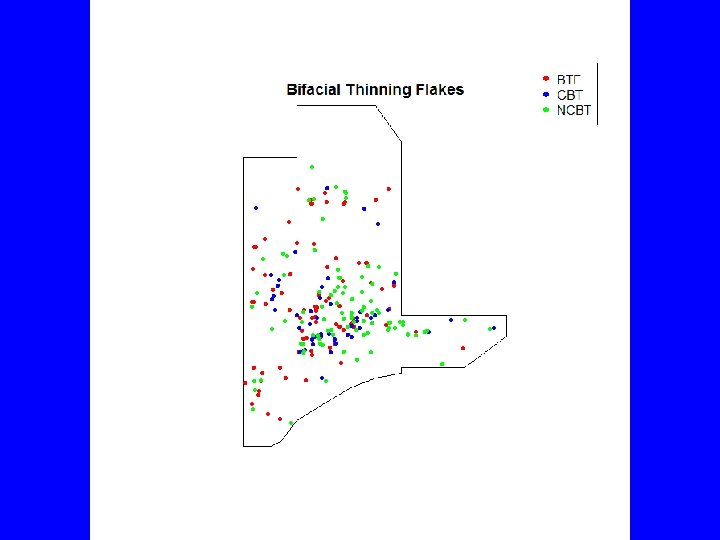
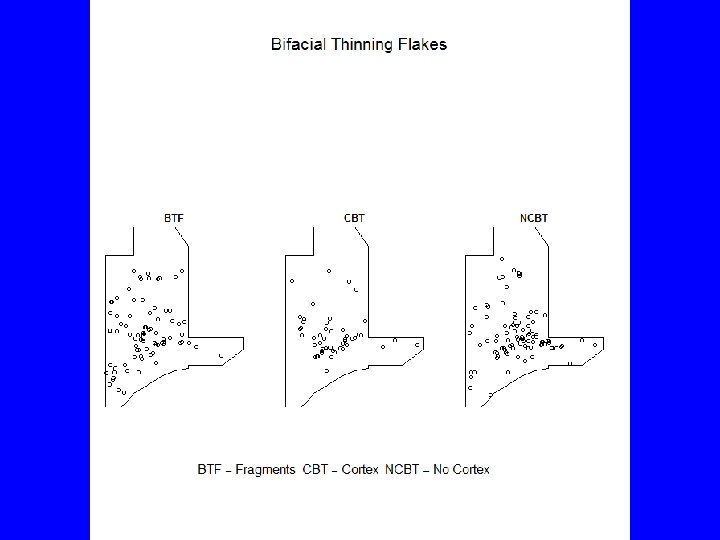
# Fix duplicate coordinates by adding 1 -2 mm to each load("C: /Users/Carlson/Documents/Courses/Anth 642/R/Data/BTF 3 a. RData") Win 3 a <- data. frame(x=c(982, 983, 984. 5, 985, 987, 986. 2, 985, 984, 983. 5, 983, 982. 7, 982. 5), y=c(1015. 5, 1021, 1022, 1021. 3, 1018, 1017. 6, 1017, 1016. 9, 1016. 8, 1016. 6, 1016. 3, 1016, 1015. 5)) # coordinates must be counterclockwise Win 3 a <- Win 3 a[order(as. numeric(rownames(Win 3 a)), decreasing=TRUE), ] library(spatstat) BTF 3 a. p <- ppp(BTF 3 a$East, BTF 3 a$North, window=owin(poly=Win 3 a, unitname=c("meter", "meters")), marks=BTF 3 a$Type) summary(BTF 3 a. p) plot(BTF 3 a. p, main="Bifacial Thinning Flakes", cex=. 75, chars=16, cols=c("red", "blue", "green")) legend("topright", c("BTF", "CBT", "NCBT"), pch=16, col=c("red", "blue", "green")) plot(split(BTF 3 a. p), main="Bifacial Thinning Flakes") mtext("BTF = Fragments CBT = Cortex NCBT = No Cortex", side=1)

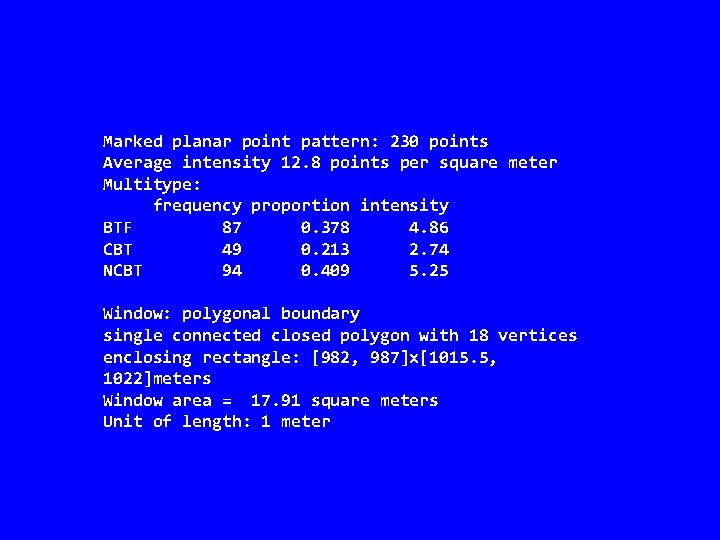
Marked planar point pattern: 230 points Average intensity 12. 8 points per square meter Multitype: frequency proportion intensity BTF 87 0. 378 4. 86 CBT 49 0. 213 2. 74 NCBT 94 0. 409 5. 25 Window: polygonal boundary single connected closed polygon with 18 vertices enclosing rectangle: [982, 987]x[1015. 5, 1022]meters Window area = 17. 91 square meters Unit of length: 1 meter

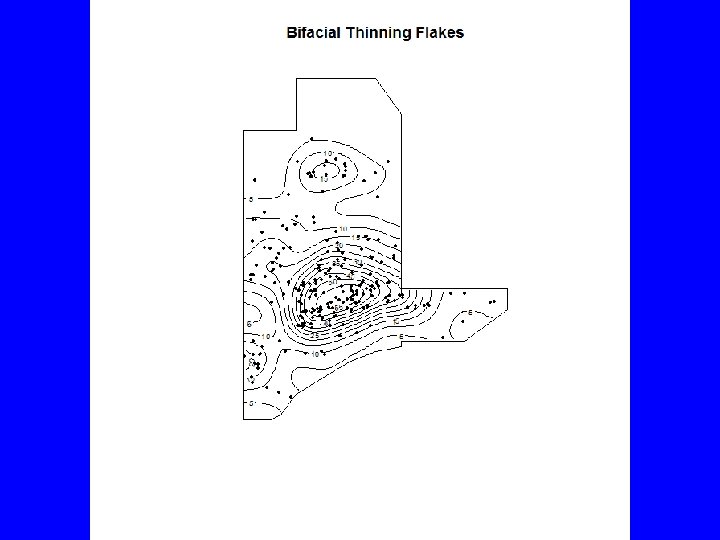
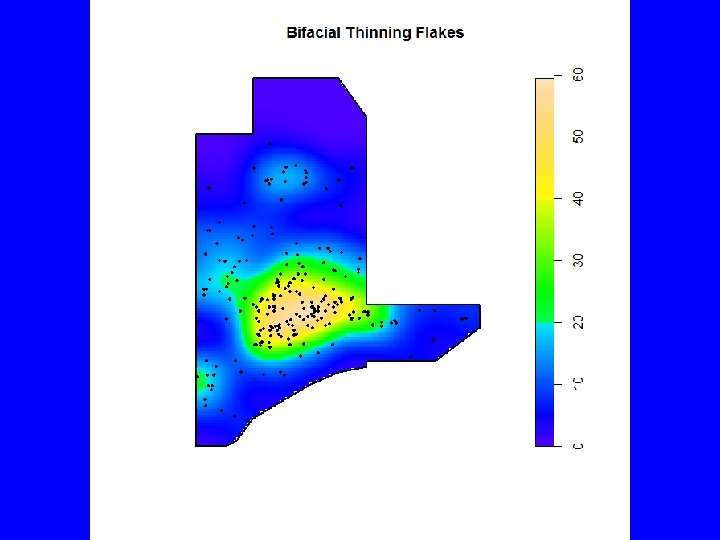
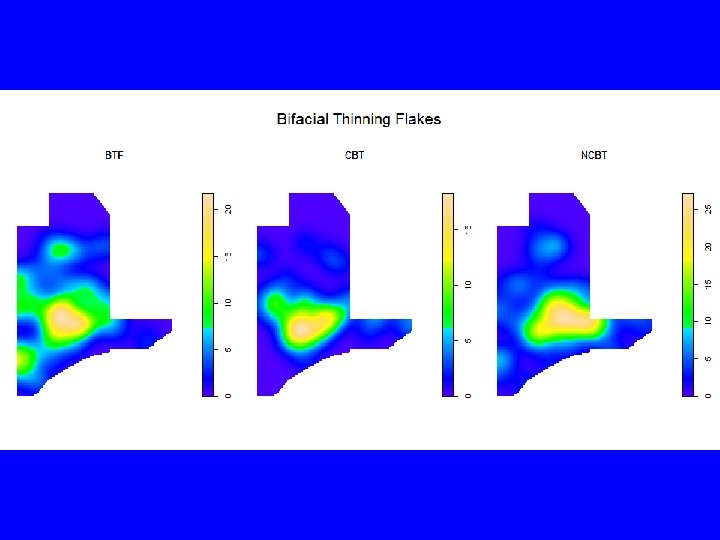
plot(982, xlim=c(982, 987), ylim=c(1015, 1022), main="Bifacial Thinning Flakes", xlab="", ylab="", axes=FALSE, asp=1, type="n") contour(density(BTF 3 a. p, adjust=. 5), add=TRUE) polygon(Win 3 a) points(BTF 3 a. p, pch=20, cex=. 75) plot(density(BTF 3 a. p, adjust=. 5), main="Bifacial Thinning Flakes") polygon(Win 3 a, lwd=2) points(BTF 3 a. p, pch=20, cex=. 75) windows(10, 5) V <- split(BTF 3 a. p) A <- lapply(V, density, adjust=. 5) plot(as. listof(A), main="Bifacial Thinning Flakes")

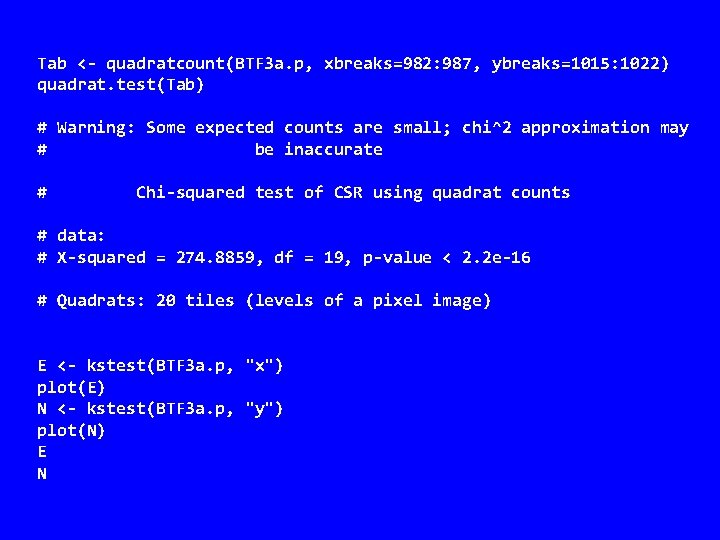
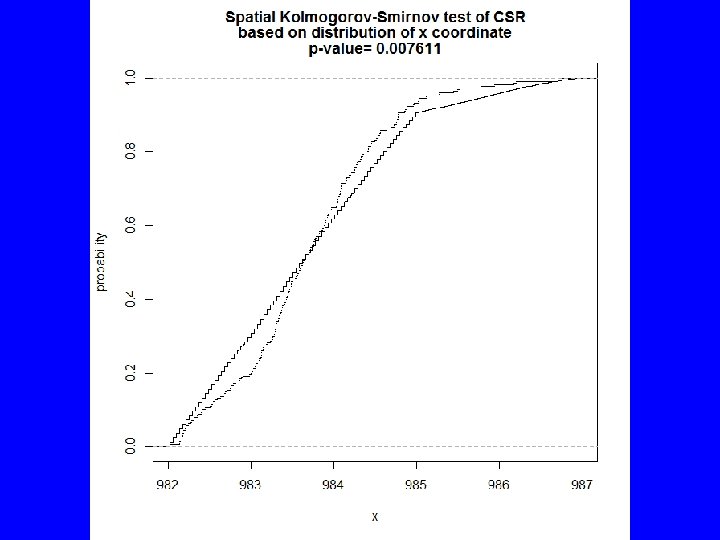
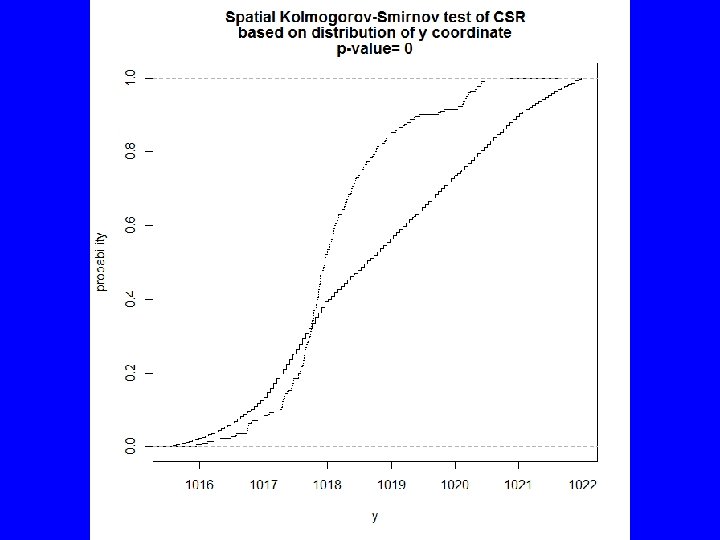
Tab <- quadratcount(BTF 3 a. p, xbreaks=982: 987, ybreaks=1015: 1022) quadrat. test(Tab) # Warning: Some expected counts are small; chi^2 approximation may # be inaccurate # Chi-squared test of CSR using quadrat counts # data: # X-squared = 274. 8859, df = 19, p-value < 2. 2 e-16 # Quadrats: 20 tiles (levels of a pixel image) E <- kstest(BTF 3 a. p, "x") plot(E) N <- kstest(BTF 3 a. p, "y") plot(N) E N

Spatial Kolmogorov-Smirnov test of CSR data: covariate 'x' evaluated at points of 'BTF 3 a. p' and transformed to uniform distribution under CSRI D = 0. 1101, p-value = 0. 007611 alternative hypothesis: two-sided Spatial Kolmogorov-Smirnov test of CSR data: covariate 'y' evaluated at points of 'BTF 3 a. p' and transformed to uniform distribution under CSRI D = 0. 2891, p-value < 2. 2 e-16 alternative hypothesis: two-sided

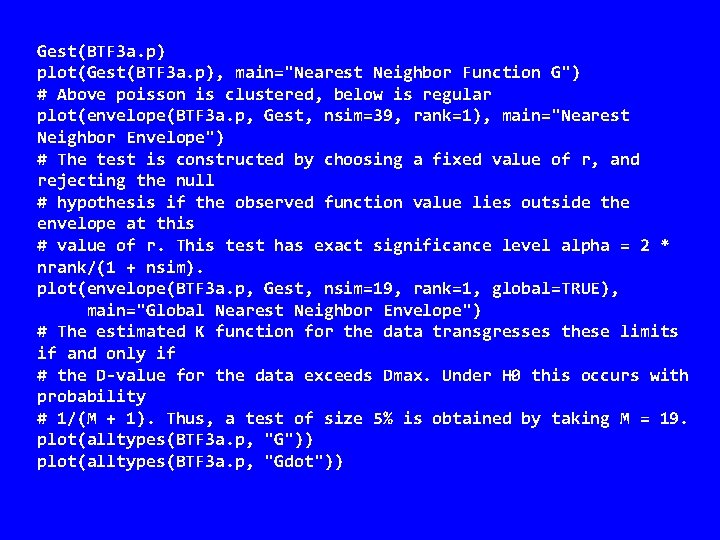
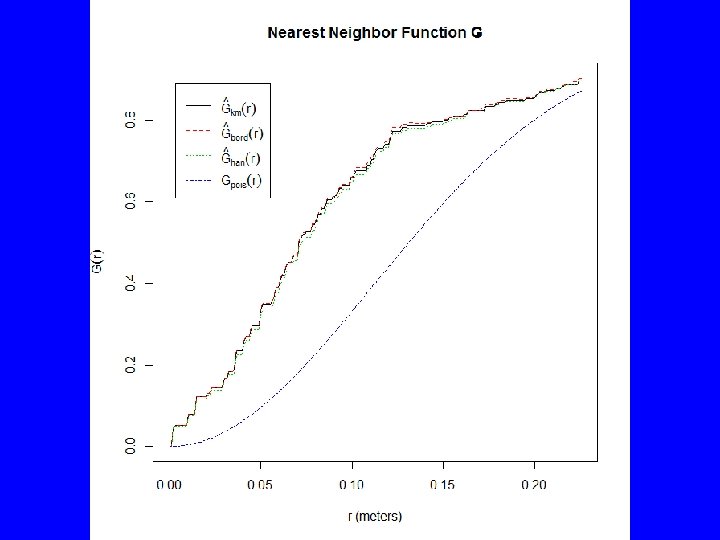
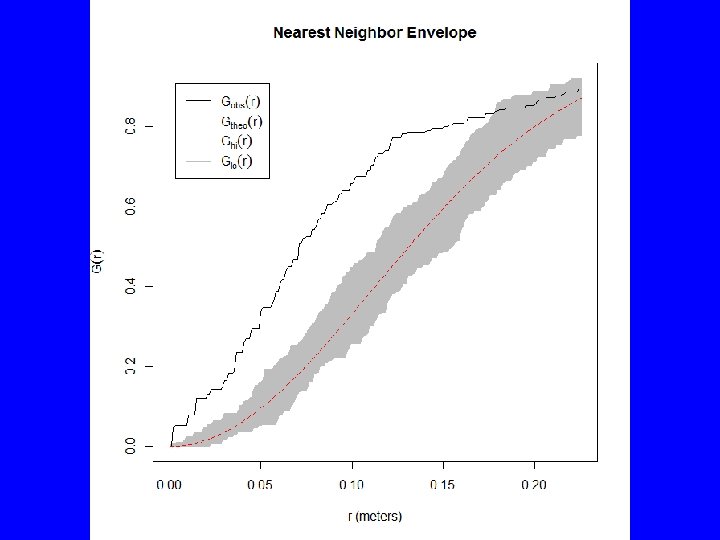
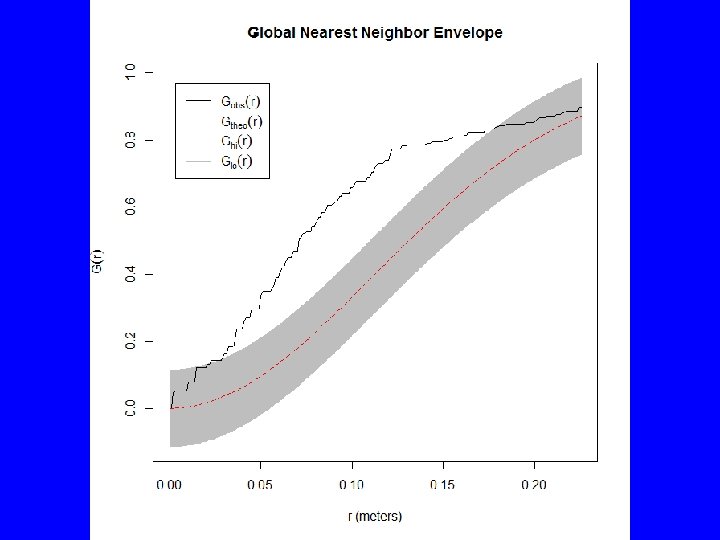
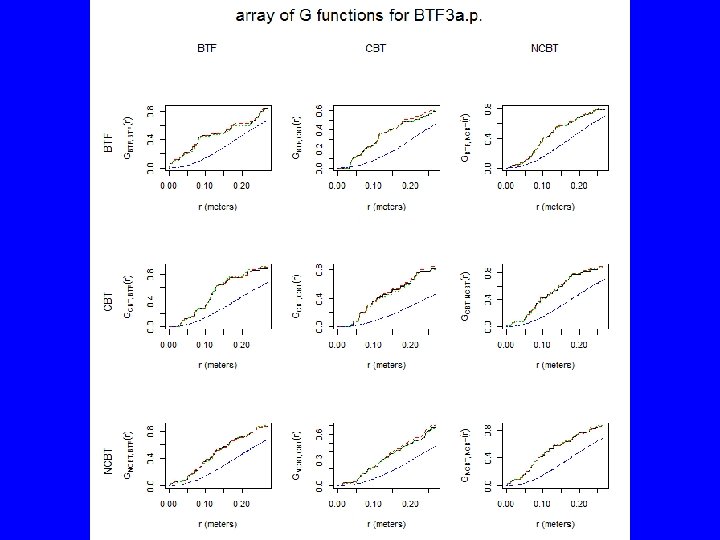
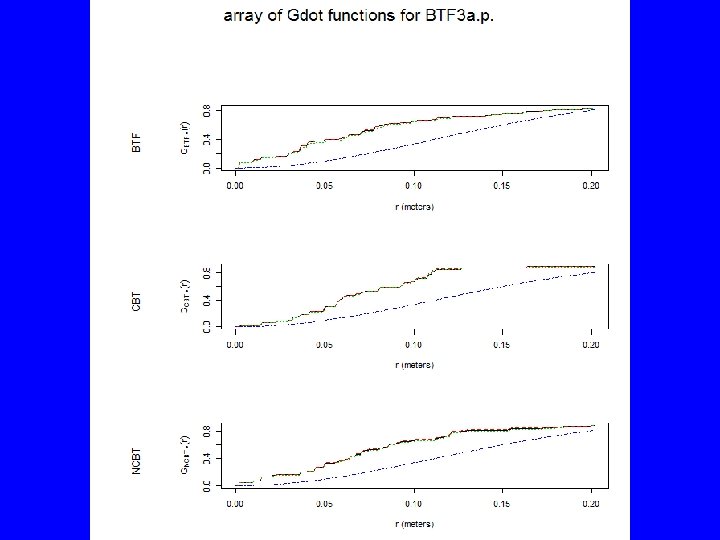
Gest(BTF 3 a. p) plot(Gest(BTF 3 a. p), main="Nearest Neighbor Function G") # Above poisson is clustered, below is regular plot(envelope(BTF 3 a. p, Gest, nsim=39, rank=1), main="Nearest Neighbor Envelope") # The test is constructed by choosing a fixed value of r, and rejecting the null # hypothesis if the observed function value lies outside the envelope at this # value of r. This test has exact significance level alpha = 2 * nrank/(1 + nsim). plot(envelope(BTF 3 a. p, Gest, nsim=19, rank=1, global=TRUE), main="Global Nearest Neighbor Envelope") # The estimated K function for the data transgresses these limits if and only if # the D-value for the data exceeds Dmax. Under H 0 this occurs with probability # 1/(M + 1). Thus, a test of size 5% is obtained by taking M = 19. plot(alltypes(BTF 3 a. p, "G")) plot(alltypes(BTF 3 a. p, "Gdot"))