Spatial Sound Encoding Including Near Field Effect Introducing

Spatial Sound Encoding Including Near Field Effect: Introducing Distance Coding Filters and a Viable, New Ambisonic Format Jérôme Daniel, France Telecom R&D jerome. daniel @ francetelecom. com ! ! !

What for a spatial sound encoding approach Ø First & Higher Order Ambisonics (HOA) o Models the acoustic reality of sound field o Homogeneous directional information o Scalable multi-channel 3 D audio format o Flexibility (transformations & decoding) Ø Part I - Fundaments of HOA: common conception and limitations o A directional encoding technique (based on amplitude panning) o Only able to handle plane waves, thus artificial sound fields Ø Part II - Recent improvements o Distance coding filters able to handle near field sources o New encoding format that supports natural or realistic sound fields o True “holophonic” rendering (comparison with WFS) o Efficient DSP tools for positional encoding

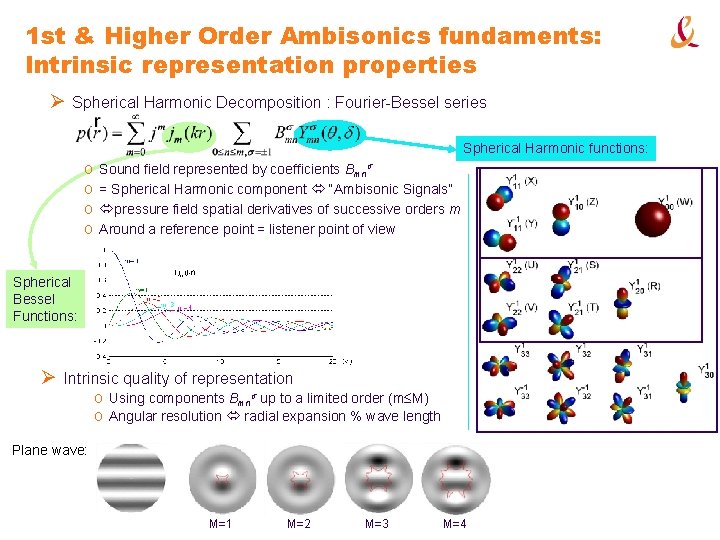
1 st & Higher Order Ambisonics fundaments: Intrinsic representation properties Ø Spherical Harmonic Decomposition : Fourier-Bessel series Spherical Harmonic functions: o o Sound field represented by coefficients Bmns = Spherical Harmonic component “Ambisonic Signals” pressure field spatial derivatives of successive orders m Around a reference point = listener point of view Spherical Bessel Functions: Ø Intrinsic quality of representation o Using components Bmns up to a limited order (m M) o Angular resolution radial expansion % wave length Plane wave: M=1 M=2 M=3 M=4

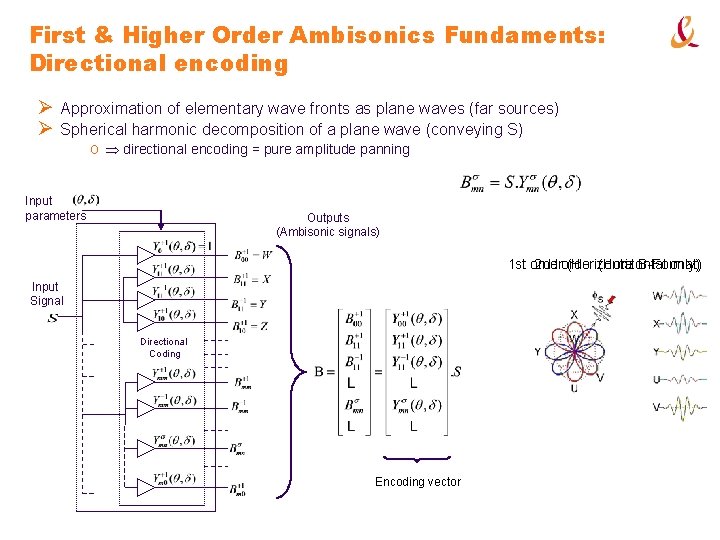
First & Higher Order Ambisonics Fundaments: Directional encoding Ø Approximation of elementary wave fronts as plane waves (far sources) Ø Spherical harmonic decomposition of a plane wave (conveying S) o directional encoding = pure amplitude panning Input parameters Outputs (Ambisonic signals) 1 st order 2 nd order (Horizontal B-Format) only) Input Signal Directional Coding Encoding vector

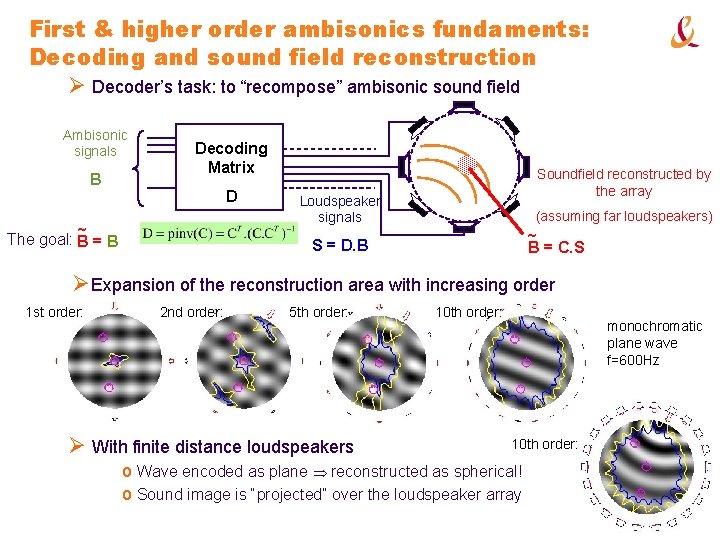
First & higher order ambisonics fundaments: Decoding and sound field reconstruction Ø Decoder’s task: to “recompose” ambisonic sound field Ambisonic signals B Decoding Matrix D ~ The goal: B = B Soundfield reconstructed by the array Loudspeaker signals (assuming far loudspeakers) ~ B = C. S S = D. B ØExpansion of the reconstruction area with increasing order 1 st order: 2 nd order: 5 th order: Ø With finite distance loudspeakers 10 th order: monochromatic plane wave f=600 Hz 10 th order: o Wave encoded as plane reconstructed as spherical! o Sound image is “projected” over the loudspeaker array

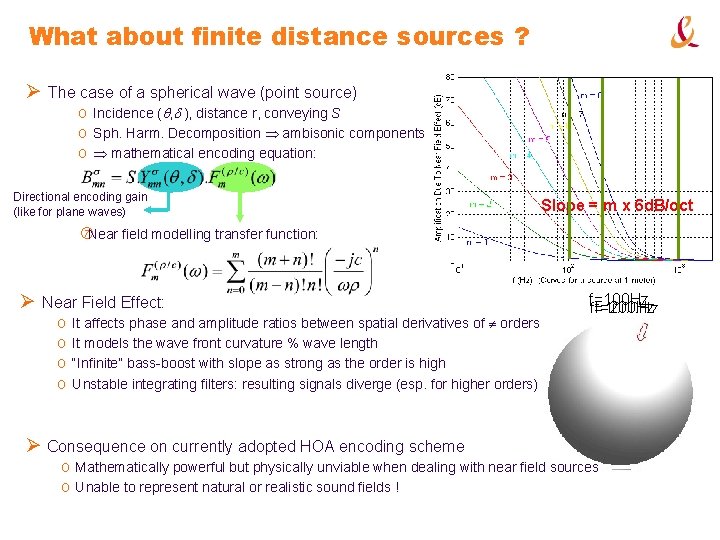
What about finite distance sources ? Ø The case of a spherical wave (point source) o Incidence (q, d ), distance r, conveying S o Sph. Harm. Decomposition ambisonic components o mathematical encoding equation: Directional encoding gain (like for plane waves) Slope = m x 6 d. B/oct Near field modelling transfer function: Ø Near Field Effect: o o It affects phase and amplitude ratios between spatial derivatives of orders It models the wave front curvature % wave length “Infinite” bass-boost with slope as strong as the order is high Unstable integrating filters: resulting signals diverge (esp. for higher orders) f=100 Hz f=200 Hz f=1000 Hz Ø Consequence on currently adopted HOA encoding scheme o Mathematically powerful but physically unviable when dealing with near field sources o Unable to represent natural or realistic sound fields !

Summary: the past, common way of looking Ambisonics… Ø In spite of featuring very attractive properties… o Homogeneous directional representation o Independent from the rendering loudspeaker layout o Scalable, flexible Ø …the commonly accepted definition of HOA suffers from limitations: o Pure amplitude panning technique: only directional encoding o Plane wave model used for encoded virtual sources l acoustically unrealistic o Unable to represent natural sound fields (at higher orders) l Neither virtual source encoding nor natural recording Ø Next: o The key to overcome these limitations o A viable, modified ambisonic format o Distance Coding (or Near Field Control) filters o Other consequences and applications

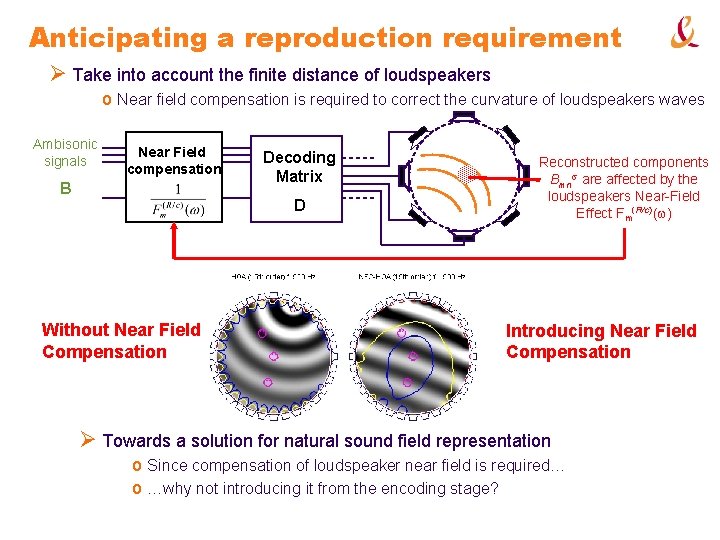
Anticipating a reproduction requirement Ø Take into account the finite distance of loudspeakers o Near field compensation is required to correct the curvature of loudspeakers waves Ambisonic signals Near Field compensation B Decoding Matrix D Without Near Field Compensation Reconstructed components Bmns are affected by the loudspeakers Near-Field Effect Fm(R/c)(w) Introducing Near Field Compensation Ø Towards a solution for natural sound field representation o Since compensation of loudspeaker near field is required… o …why not introducing it from the encoding stage?

Distance coding filters & viable representation Ø Practicable “Near Field Coding” (NFC) filters o o Model loudspeaker NF compensation + virtual source NF effect … at the same time, from the encoding stage Amplification depending on r % R Positional encoding = directional + distance coding Ø “Near Field pre-Compensated” HOA format (NFC-HOA) o Components defined as: o. Its supports natural/realistic sound fields o. It merely requires a “classic” matrix decoding o. Implicit parameter = “reference distance” R = loudspeaker array radius o. Can further adapt to any other loudspeaker distance R’ using NFC filters l(correct the wave field curvature) Finite amplification: m x 20 log 10(R/r)

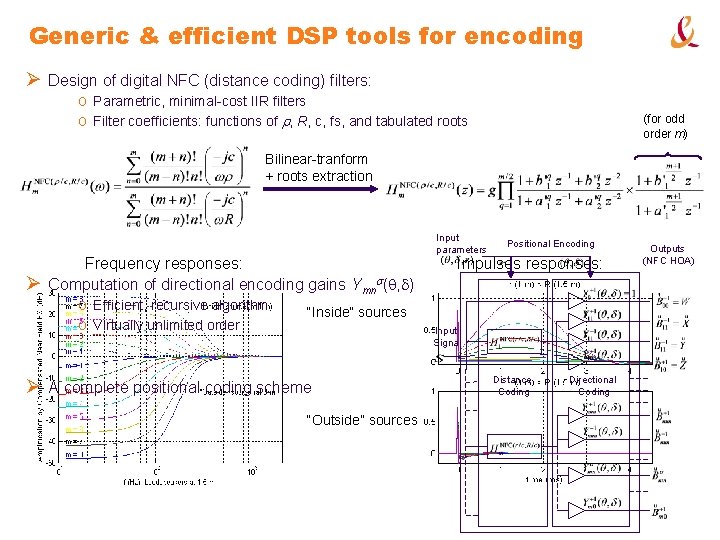
Generic & efficient DSP tools for encoding Ø Design of digital NFC (distance coding) filters: o Parametric, minimal-cost IIR filters o Filter coefficients: functions of r, R, c, fs, and tabulated roots (for odd order m) Bilinear-tranform + roots extraction Ø Frequency responses: Computation of directional encoding gains Ymns(q, d) o Efficient, recursive algorithm “Inside” sources o Virtually unlimited order Ø A complete positional coding scheme “Outside” sources Input parameters Positional Encoding Impulses responses: Input Signal Distance Coding Directional Coding Outputs (NFC HOA)

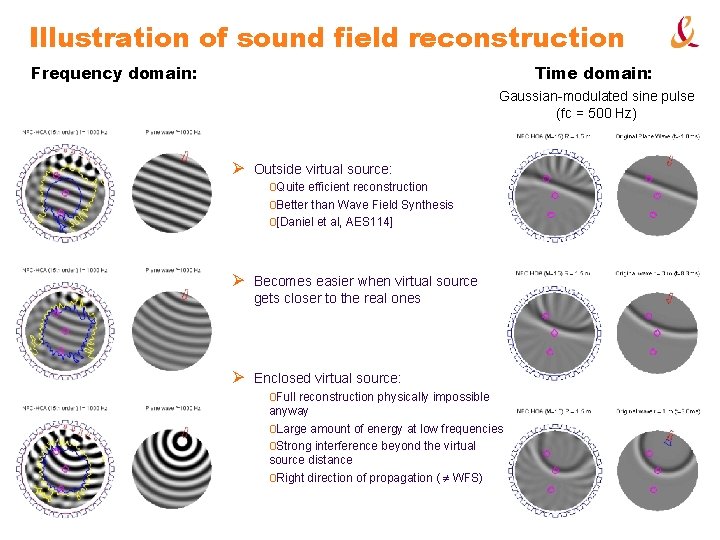
Illustration of sound field reconstruction Frequency domain: Time domain: Gaussian-modulated sine pulse (fc = 500 Hz) Ø Outside virtual source: o. Quite efficient reconstruction o. Better than Wave Field Synthesis o[Daniel et al, AES 114] Ø Becomes easier when virtual source gets closer to the real ones Ø Enclosed virtual source: o. Full reconstruction physically impossible anyway o. Large amount of energy at low frequencies o. Strong interference beyond the virtual source distance o. Right direction of propagation ( WFS)

Other consequences and applications Ø HOA recording systems become practicable o …by introducing NF compensation at the stage of the mic signal processing o otherwise: equalization filters are unstable [Daniel et al, AES 114] and natural sound fields cannot be physically represented o 4 th order microphone prototype: being experimented at FTR&D Labs Ø Accurate binaural synthesis of close sources o “Virtual Ambisonics” l = head-centred ambisonics + binaural synthesis of virtual loudspeakers l Supports sound field rotations, thus head-tracking adaptation o “Ear-centred double virtual ambisonics” l Binaural B-format encoding scheme enriched by NF-Coding filters l More accurate than “head-centred virtual ambisonics” l … but doesn’t support rotations once the encoding is done

Conclusions Ø Recall of some HOA fundaments and properties o Powerful mathematical approach o Highly versatile 3 D sound field representation Ø New: positional coding completed by distance coding o Efficient digital Near Field Control filters o Take care of the special case of enclosed sources Ø A New, Viable HOA format : NFC HOA o It enables all HOA nice features considering natural/realistic sound fields o It doesn’t necessarily interest only systems with very numerous loudspeakers

Work in progress Ø Evaluation of holophonic sound imaging over 48 loudspeakers o Up to 15 th order Ambisonics o Comparison of HOA and WFS for outside and enclosed sources o In the context of the CARROUSO project Ø Experimentation of a 4 th order ambisonic microphone o 32 capsules over a sphere Ø Specification of a generic HOA format o In MPEG-4 (for Audio. BIFS V 3) l => handle multi-channel audio streams as scalable 3 D sound fields o As a extension of the Wave file format o Detailed propositions in the paper