Spatial Interpolation in GIS Zhongwei Liu Ph D

Spatial Interpolation in GIS Zhongwei Liu, Ph. D. School of Environmental and Public Affairs University of Nevada, Las Vegas Zhongwei. Liu@unlv. edu 2/18/2010

Outline Ø Spatial interpolation – Linear interpolation – Nonlinear interpolation Ø Case study Ø Tutorials 2

Operations on surfaces Ø Interpolation – Linear interpolation – Nonlinear interpolation 3

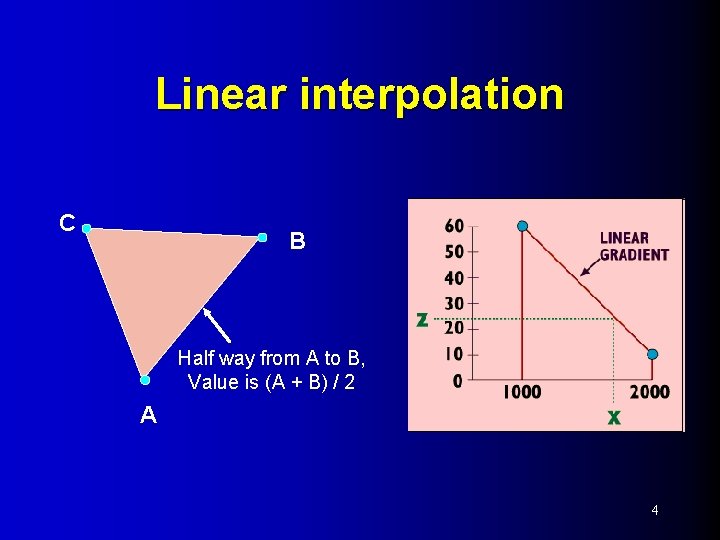
Linear interpolation C B Half way from A to B, Value is (A + B) / 2 A 4

Nonlinear interpolation Ø Basic types – Inverse Distance Weighted (IDW) – Spline: fits a minimum-curvature surface through the input points – Kriging: use virogram to determine the neighborhood for interpolation 5

1. Inverse Distance Weighted (IDW) Ø Each input point has a local influence that diminishes with distance Ø an implementation of Tobler’s First Law of Geography Ø Use inverse distance as weight for summation of values in a neighborhood Ø The new [Hmin, Hmax] is within the original [Hmin, Hmax] w 1=1/d 1, w 2=1/d 2, w 3=1/d 3 w=w 1+w 2+w 3 hx=h 1*w 1/w+h 2*w 2/w+h 3*w 3/w =(h 1*w 1+h 2*w 2+h 3*w 3)/w h 1 d 2 h 2 d 3 hx=? ? ? h 3 6

A potentially undesirable characteristic of IDW interpolation 4. 5 Ø This set of six data points clearly suggests a hill profile. But in areas where there is little or no data the interpolator will move towards the overall mean. Blue line shows the profile interpolated by IDW 4 3. 5 3 2. 5 2 1. 5 1 97 100 91 94 88 85 82 79 76 70 73 64 67 61 55 58 52 46 49 43 37 40 34 28 31 25 22 19 16 13 7 10 1 0 4 0. 5 7

8

2. Spline Ø Like bending a sheet of rubber to pass through points while minimizing curvature of that sheet repeatedly applies a smoothing equation (polynomial) to the surface Ø Resulting surface passes through all points Ø Best for gently varying surfaces, not for rugged ones (can overshoot data values) 9

Spline 10

11

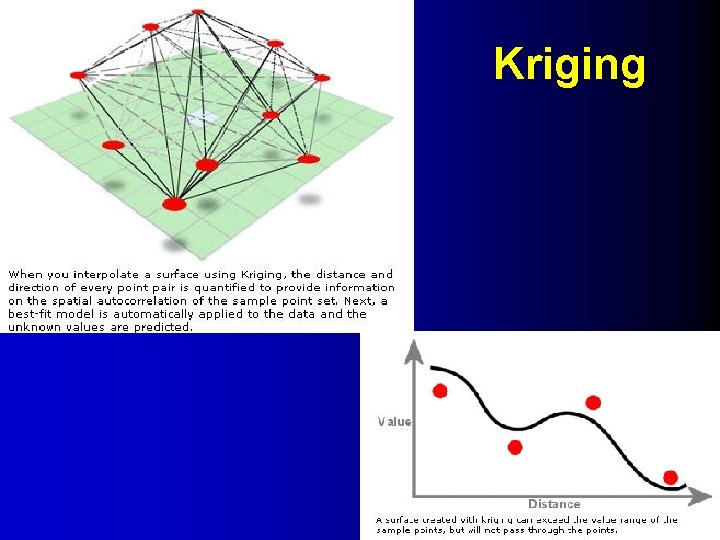
variation 3. Kriging Ø Use virogram to determine the neighborhood for interpolation d* d – Based on spatial auto-correlation – Use d* to define the neighborhood Ø Fits function to – Specified number of points OR – All points within a window of specified radius Ø Assumes distance or direction between sample points shows a spatial correlation that help describe the surface. Ø Kriging differs from the methods discussed so far because kriging can assess the quality of prediction with estimated prediction errors. 12

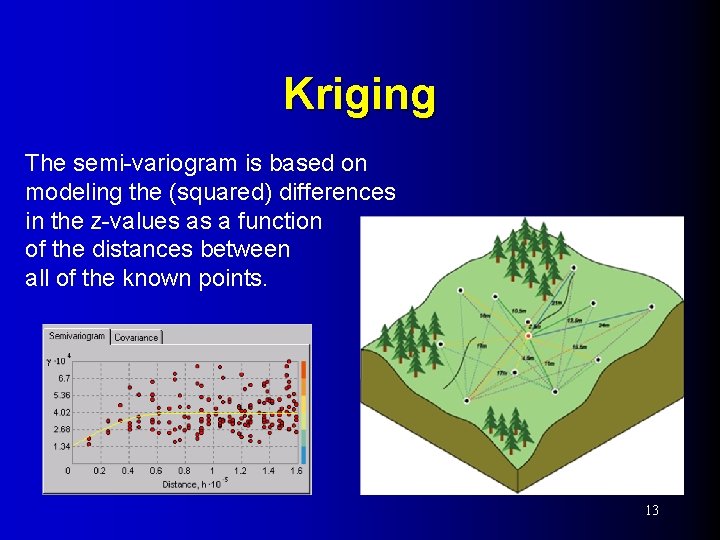
Kriging The semi-variogram is based on modeling the (squared) differences in the z-values as a function of the distances between all of the known points. 13

Kriging 14

15

Cross validation Ø Removing one of the n observation points and using the remaining n-1 points to predict its value. Ø Error = observed - predicted 16

IDW vs. Kriging Ø Kriging appears to give a more “natural” look to the data Ø Kriging avoids the “bulls eye” effect Ø Kriging gives us a standard error 17

Which Method to Use? Ø IDW - assumes variable decreases in influence w/distance from sampled location – Interpolating a surface of consumer purchasing power for a retail store Ø Spline - best for surfaces that are already smooth – Elevations, water table heights, etc. Ø Kriging - if you already know correlated distances or directional bias in data – Geology, soil science 18

Interpolation Software Ø Arc. GIS 9. x with Geostatistical Analyst Ø Arc. View 3. x Ø Surfer (Golden Software) Ø Surface II package (Kansas Geological Survey) Ø GEOEAS (EPA) Ø Spherekit (NCGIA, UCSB) Ø Matlab 19

The Everglades Ø Ø 10, 000 islands (tree islands) 6 Inches beneath sea level Average annual rainfall 130 cm Over 2, 000 plant species http: //sofia. usgs. gov/eden 20

Models based on spatial interpolation for Everglades restoration Ø Everglades – Subtropical wetland – Dry (Oct. May) and wet (Jun. - Sept. ) seasons wet prairie sawgrass marsh wet prairie tree islands slough alligator holes Ø Everglades restoration – $7. 8 billion Source: www. broward. edu. 21

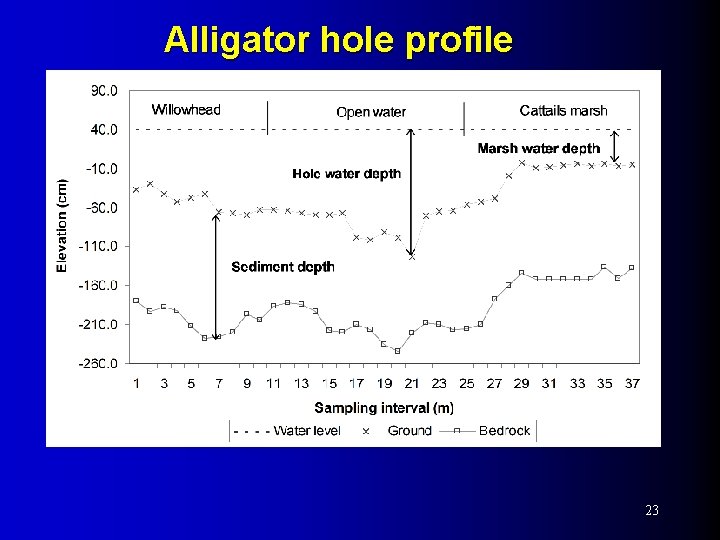
Alligator hole & water level and depth Ø American Alligator – Top predator, keystone species, ecosystem engineer in Florida Everglades Ø Alligator Hole – Small but persistent ponds excavated and maintained by alligators – Dry-season refugia – Nest, colonization, and foraging sites 22

Alligator hole profile 23

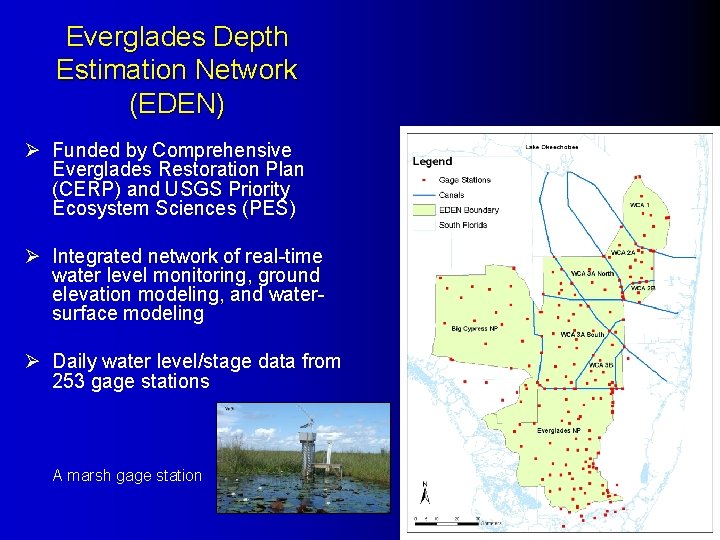
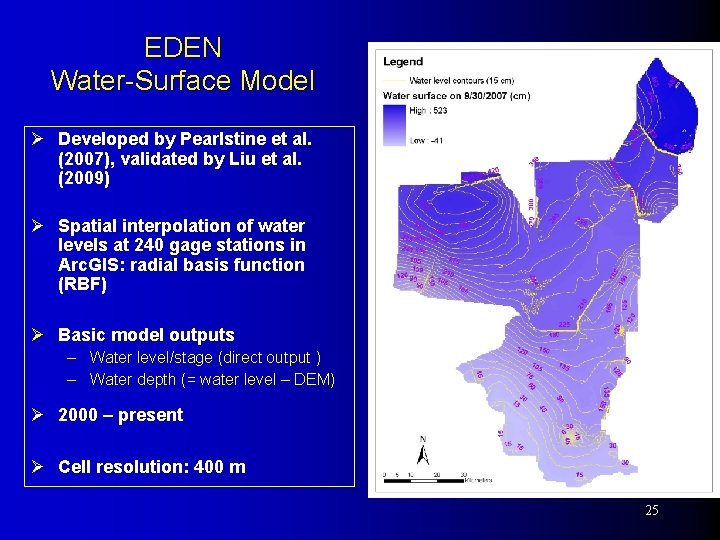
Everglades Depth Estimation Network (EDEN) Ø Funded by Comprehensive Everglades Restoration Plan (CERP) and USGS Priority Ecosystem Sciences (PES) Ø Integrated network of real-time water level monitoring, ground elevation modeling, and watersurface modeling Ø Daily water level/stage data from 253 gage stations A marsh gage station 24

EDEN Water-Surface Model Ø Developed by Pearlstine et al. (2007), validated by Liu et al. (2009) Ø Spatial interpolation of water levels at 240 gage stations in Arc. GIS: radial basis function (RBF) Ø Basic model outputs – Water level/stage (direct output ) – Water depth (= water level – DEM) Ø 2000 – present Ø Cell resolution: 400 m 25

EDEN DEM (Digital Elevation Model) Ø Developed by Jones and Price (2007) Ø Spatial interpolation of High Accuracy Elevation Data (HAED) in Arc. GIS: kriging Ø HAED elevation points collected via Airborne Height Finder and airboat Ø Cell resolution: 400 m 26

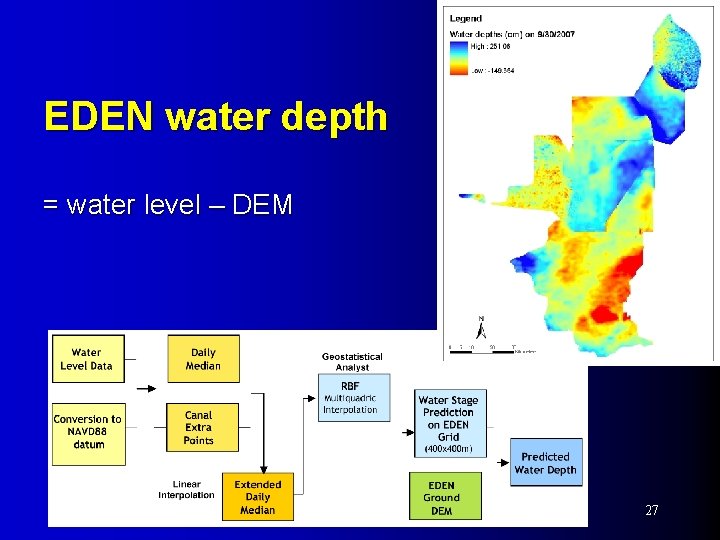
EDEN water depth = water level – DEM 27

Revisions of EDEN Water. Surface Model Ø Modification to the canals files to better represent NE Shark River Slough in the area of Tamiami Trail and L 67 Extension 28

Revisions of EDEN Water. Surface Model Ø Reparameterization of the EDEN watersurface model – With new gage stations (including coastal) – With resurveyed gage information (locations, water levels) in NAVD 88 datum – RBF surface interpolation by EDEN subregions 29

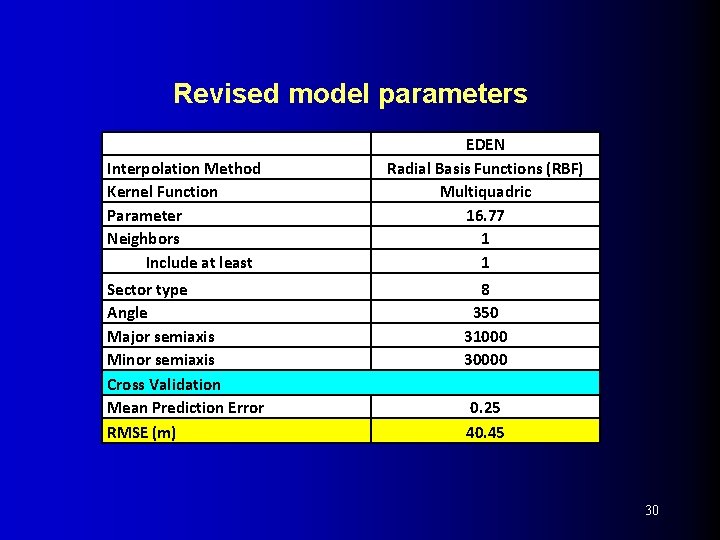
Revised model parameters Interpolation Method Kernel Function Parameter Neighbors Include at least Sector type Angle Major semiaxis Minor semiaxis Cross Validation Mean Prediction Error RMSE (m) EDEN Radial Basis Functions (RBF) Multiquadric 16. 77 1 1 8 350 31000 30000 0. 25 40. 45 30

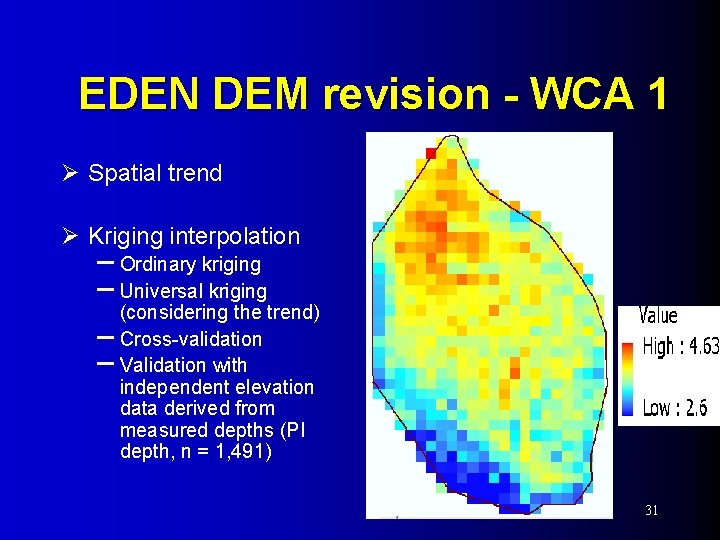
EDEN DEM revision - WCA 1 Ø Spatial trend Ø Kriging interpolation – Ordinary kriging – Universal kriging (considering the trend) – Cross-validation – Validation with independent elevation data derived from measured depths (PI depth, n = 1, 491) 31

32

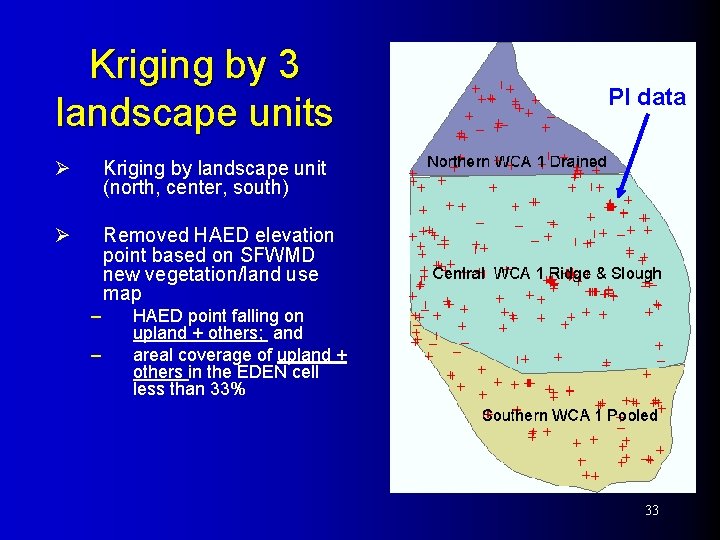
Kriging by 3 landscape units Ø Kriging by landscape unit (north, center, south) Ø Removed HAED elevation point based on SFWMD new vegetation/land use map – – PI data HAED point falling on upland + others; and areal coverage of upland + others in the EDEN cell less than 33% 33

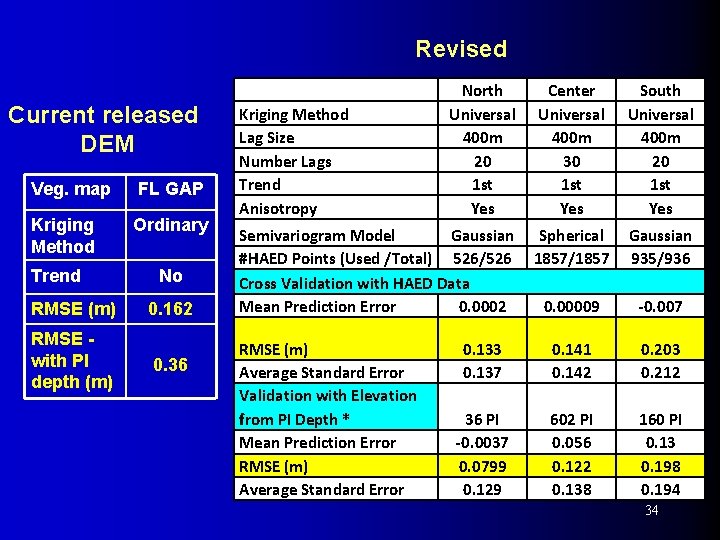
Revised Current released DEM Veg. map FL GAP Kriging Method Ordinary Trend RMSE (m) RMSE with PI depth (m) No 0. 162 0. 36 North Universal 400 m 20 1 st Yes Center Universal 400 m 30 1 st Yes South Universal 400 m 20 1 st Yes Semivariogram Model Gaussian #HAED Points (Used /Total) 526/526 Cross Validation with HAED Data Mean Prediction Error 0. 0002 Spherical 1857/1857 Gaussian 935/936 0. 00009 -0. 007 0. 133 0. 137 0. 141 0. 142 0. 203 0. 212 36 PI -0. 0037 0. 0799 0. 129 602 PI 0. 056 0. 122 0. 138 160 PI 0. 13 0. 198 0. 194 Kriging Method Lag Size Number Lags Trend Anisotropy RMSE (m) Average Standard Error Validation with Elevation from PI Depth * Mean Prediction Error RMSE (m) Average Standard Error 34