Spatial Indexing for NN retrieval Rtree Rtrees n

Spatial Indexing for NN retrieval R-tree

R-trees n n n A multi-way external memory tree Index nodes and data (leaf) nodes All leaf nodes appear on the same level Every node contains between m and M entries The root node has at least 2 entries (children) Extension of B+-tree to multiple dimensions

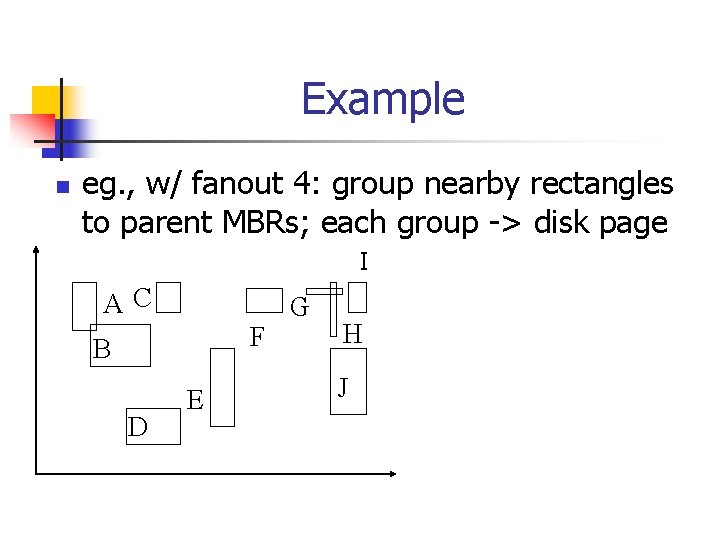
Example n eg. , w/ fanout 4: group nearby rectangles to parent MBRs; each group -> disk page I AC F B D E G H J

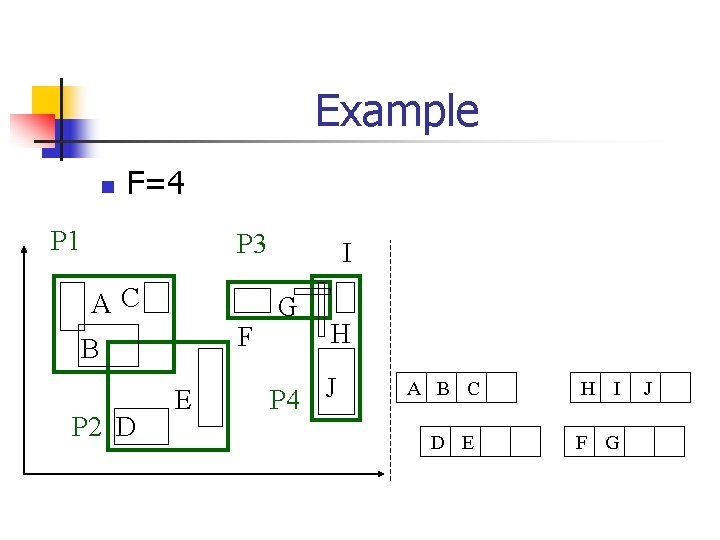
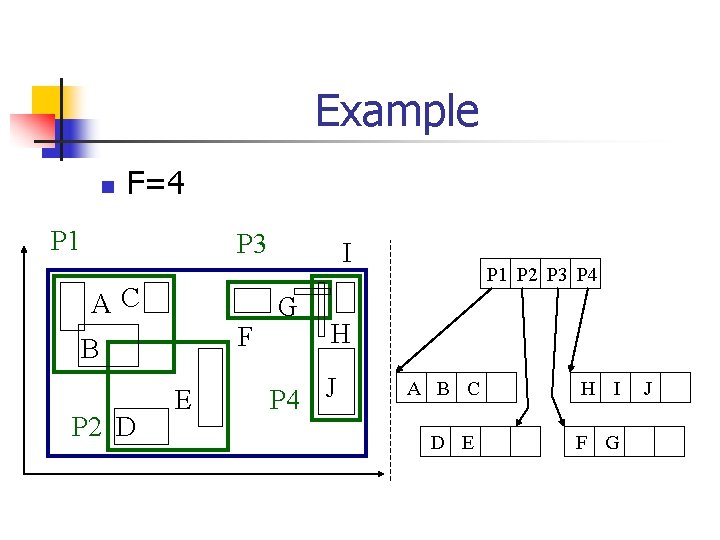
Example n F=4 P 1 P 3 AC F B P 2 D E I G H P 4 J A B C D E H I F G J

Example n F=4 P 1 P 3 AC F B P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E H I F G J

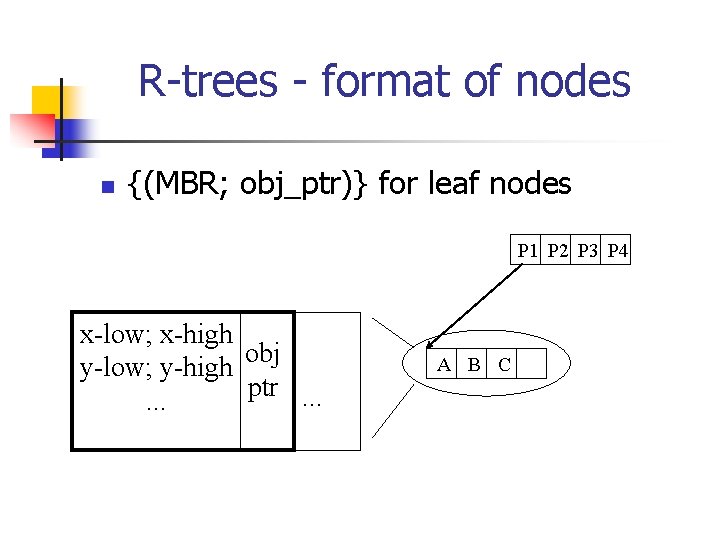
R-trees - format of nodes n {(MBR; obj_ptr)} for leaf nodes P 1 P 2 P 3 P 4 x-low; x-high obj y-low; y-high ptr. . . A B C

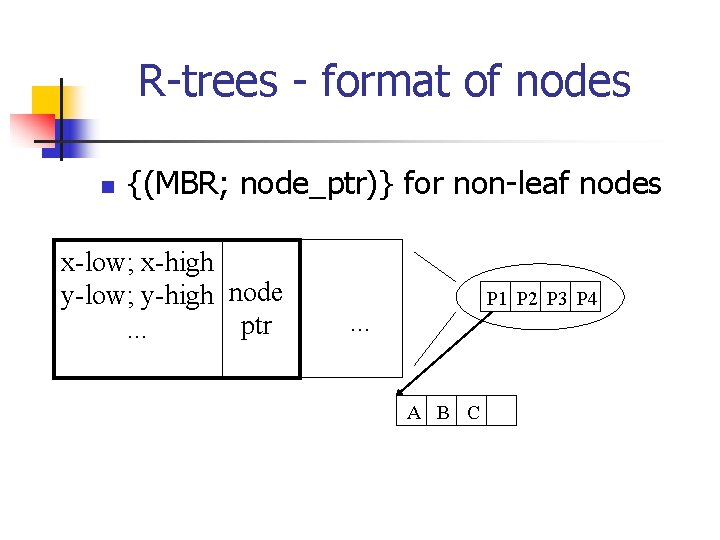
R-trees - format of nodes n {(MBR; node_ptr)} for non-leaf nodes x-low; x-high y-low; y-high node ptr. . . P 1 P 2 P 3 P 4 . . . A B C

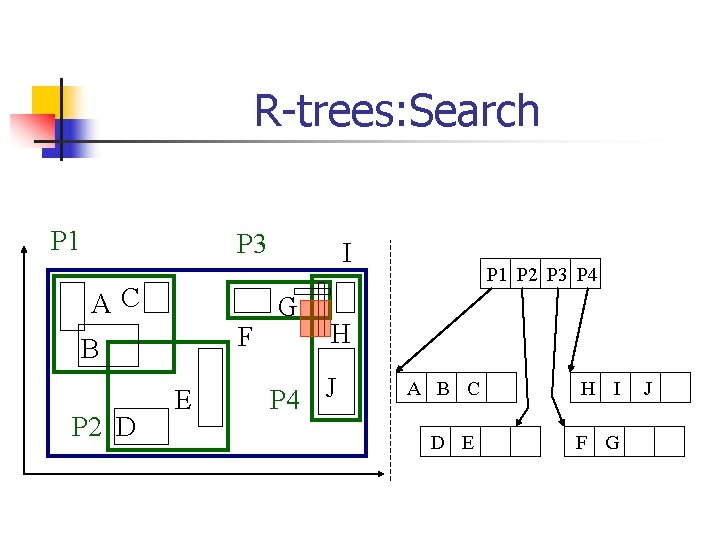
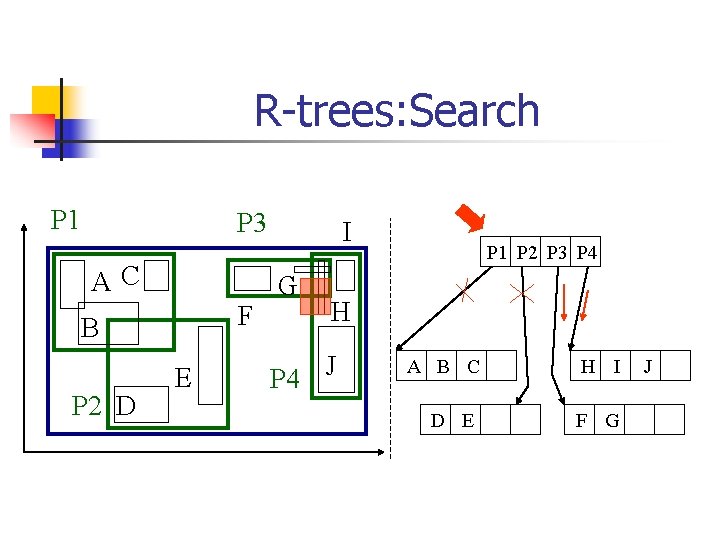
R-trees: Search P 1 P 3 AC F B P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E H I F G J

R-trees: Search P 1 P 3 AC F B P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E H I F G J

R-trees: Search n Main points: n n every parent node completely covers its ‘children’ a child MBR may be covered by more than one parent - it is stored under ONLY ONE of them. (ie. , no need for dup. elim. ) a point query may follow multiple branches. everything works for any(? ) dimensionality

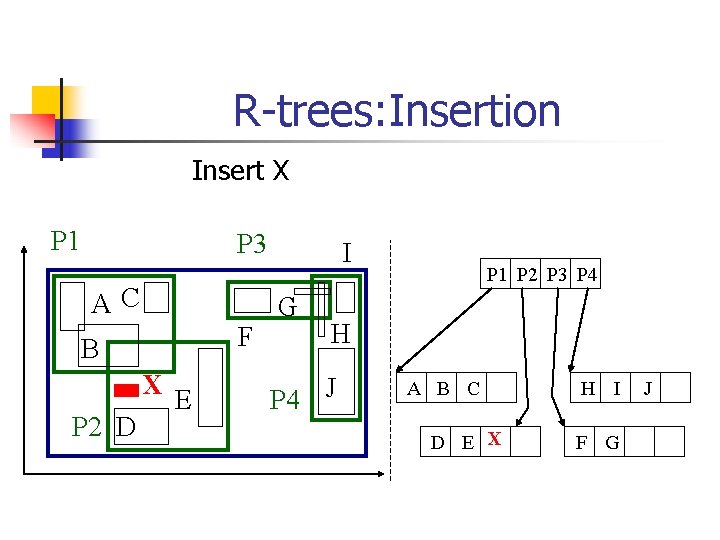
R-trees: Insertion Insert X P 1 P 3 AC F B X P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E X H I F G J

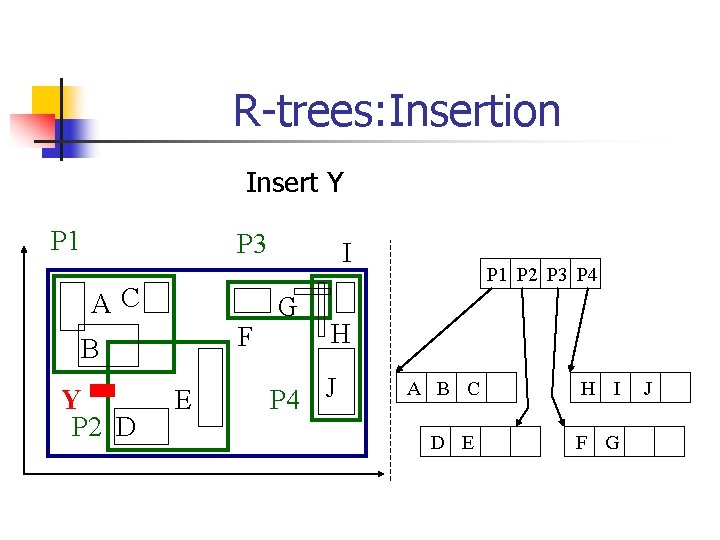
R-trees: Insertion Insert Y P 1 P 3 AC F B Y P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E H I F G J

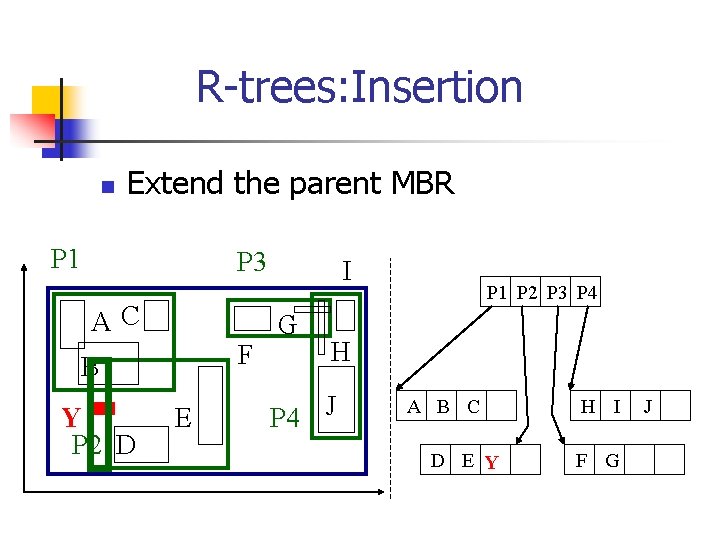
R-trees: Insertion n Extend the parent MBR P 1 P 3 AC F B Y P 2 D E I G P 1 P 2 P 3 P 4 H P 4 J A B C D E Y H I F G J

R-trees: Insertion n How to find the next node to insert the new object? n n Using Choose. Leaf: Find the entry that needs the least enlargement to include Y. Resolve ties using the area (smallest) Other methods (later)

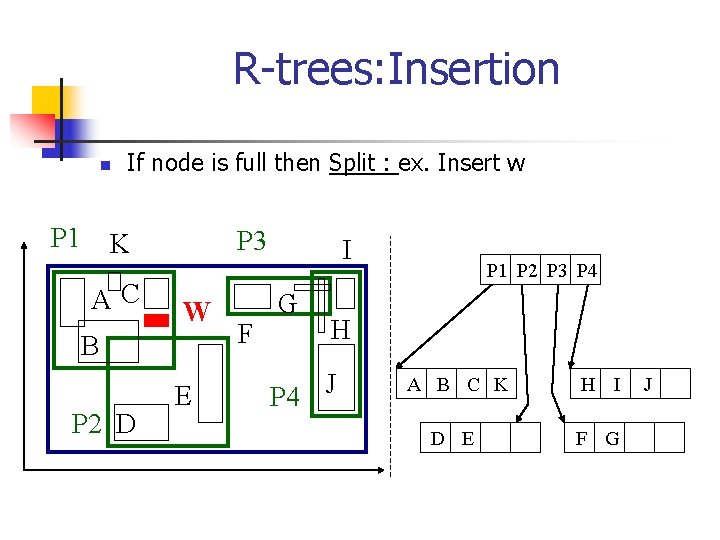
R-trees: Insertion n P 1 If node is full then Split : ex. Insert w P 3 K AC W B P 2 D E F I G P 1 P 2 P 3 P 4 H P 4 J A B C K H I D E F G J

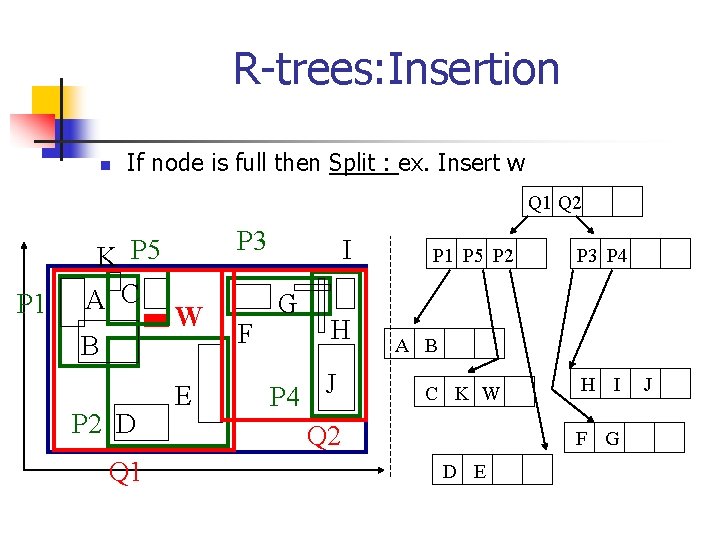
R-trees: Insertion n If node is full then Split : ex. Insert w Q 1 Q 2 P 1 K P 5 A C B P 2 D Q 1 P 3 W E F I G H P 4 J Q 2 P 1 P 5 P 2 P 3 P 4 A B C K W H I F G D E J

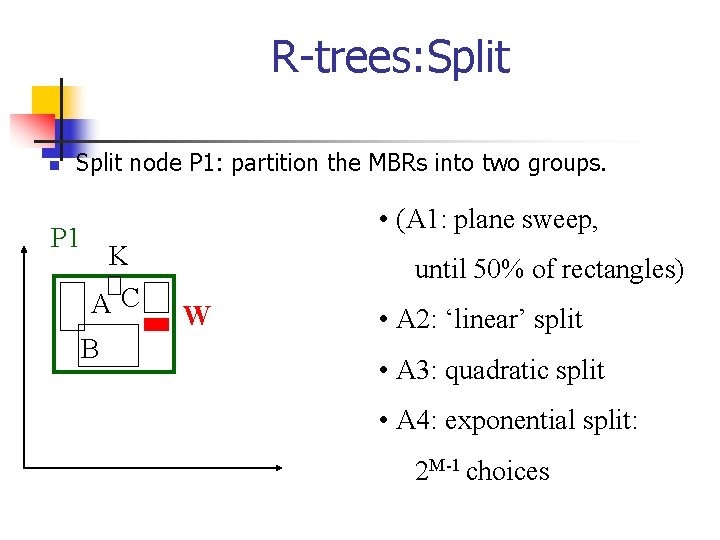
R-trees: Split node P 1: partition the MBRs into two groups. • (A 1: plane sweep, P 1 K AC B until 50% of rectangles) W • A 2: ‘linear’ split • A 3: quadratic split • A 4: exponential split: 2 M-1 choices

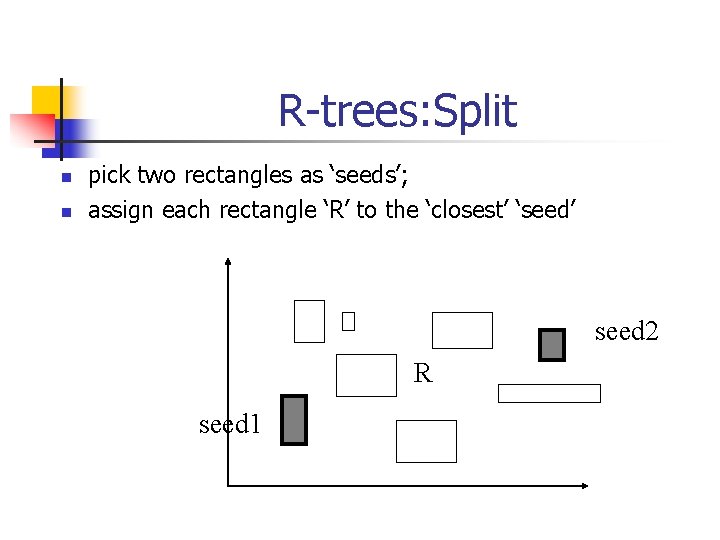
R-trees: Split n n pick two rectangles as ‘seeds’; assign each rectangle ‘R’ to the ‘closest’ ‘seed’ seed 2 R seed 1

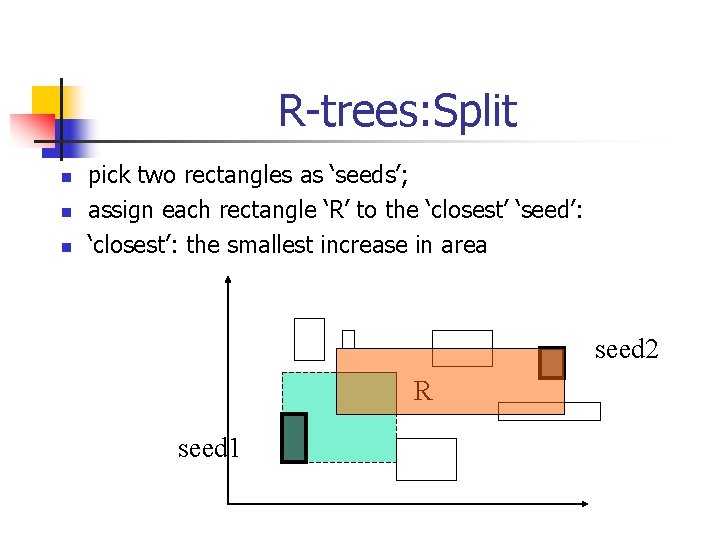
R-trees: Split n n n pick two rectangles as ‘seeds’; assign each rectangle ‘R’ to the ‘closest’ ‘seed’: ‘closest’: the smallest increase in area seed 2 R seed 1

R-trees: Split n How to pick Seeds: n Linear: Find the highest and lowest side in each dimension, normalize the separations, choose the pair with the greatest normalized separation n Quadratic: For each pair E 1 and E 2, calculate the rectangle J=MBR(E 1, E 2) and d= J-E 1 -E 2. Choose the pair with the largest d

R-trees: Insertion n n Use the Choose. Leaf to find the leaf node to insert an entry E If leaf node is full, then Split, otherwise insert there n n Propagate the split upwards, if necessary Adjust parent nodes

R-Trees: Deletion n Find the leaf node that contains the entry E Remove E from this node If underflow: n Eliminate the node by removing the node entries and the parent entry n Reinsert the orphaned (other entries) into the tree using Insert

R-trees: Variations n n n R+-tree: DO not allow overlapping, so split the objects (similar to z-values) R*-tree: change the insertion, deletion algorithms (minimize not only area but also perimeter, forced re-insertion ) Hilbert R-tree: use the Hilbert values to insert objects into the tree

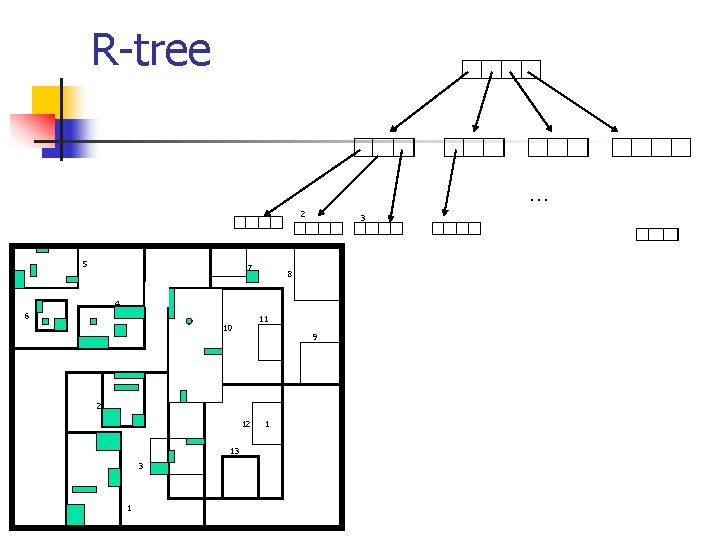
R-tree … 2 5 7 3 8 4 6 11 10 9 2 12 13 3 1 1

R-trees - Range search pseudocode: check the root for each branch, if its MBR intersects the query rectangle apply range-search (or print out, if this is a leaf)

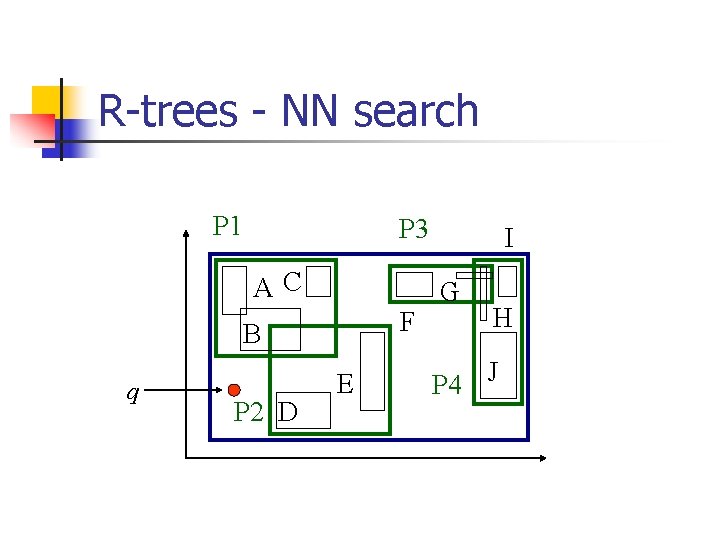
R-trees - NN search P 1 P 3 AC F B q P 2 D E I G H P 4 J

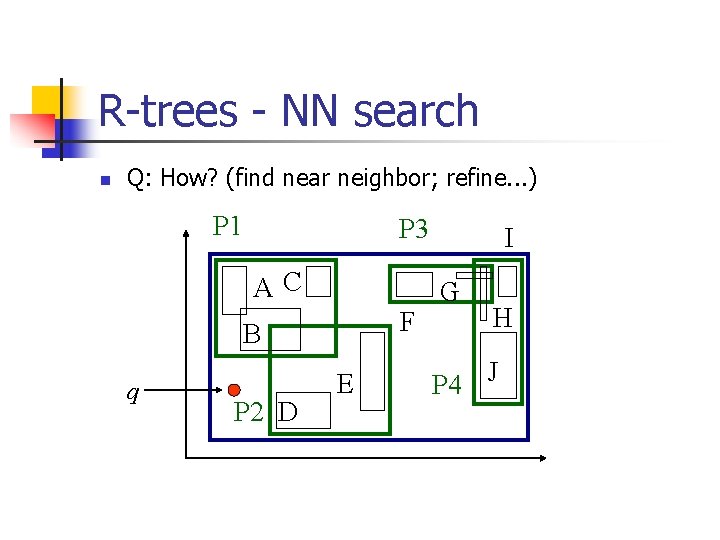
R-trees - NN search n Q: How? (find near neighbor; refine. . . ) P 1 P 3 AC F B q P 2 D E I G H P 4 J

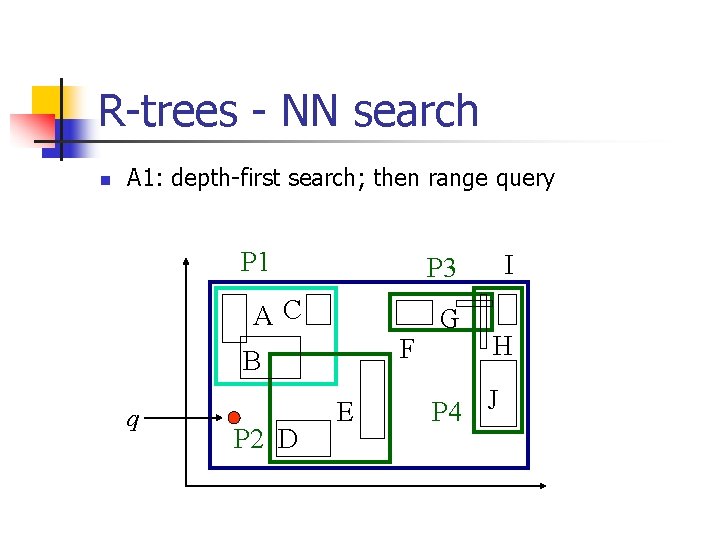
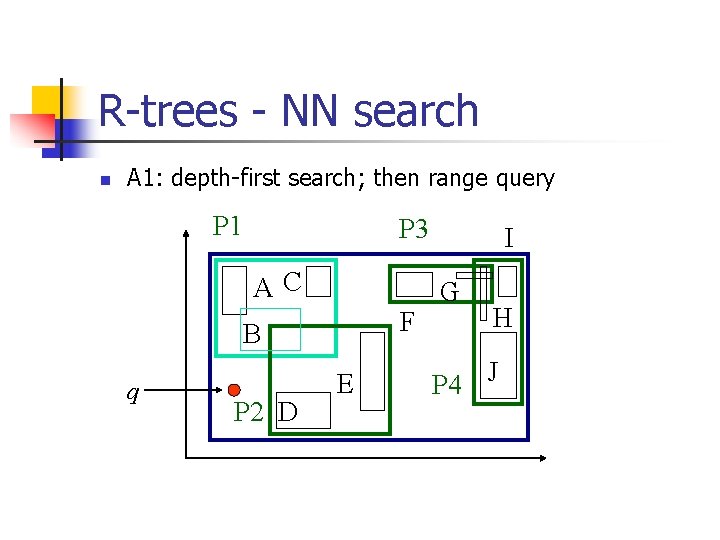
R-trees - NN search n A 1: depth-first search; then range query P 1 AC F B q P 2 D I P 3 E G H P 4 J

R-trees - NN search n A 1: depth-first search; then range query P 1 P 3 AC F B q P 2 D E I G H P 4 J

R-trees - NN search n A 1: depth-first search; then range query P 1 P 3 AC F B q P 2 D E I G H P 4 J

R-trees - NN search: Branch and Bound n n A 2: [Roussopoulos+, sigmod 95]: n At each node, priority queue, with promising MBRs, and their best and worst-case distance main idea: Every face of any MBR contains at least one point of an actual spatial object!

MBR face property n n MBR is a d-dimensional rectangle, which is the minimal rectangle that fully encloses (bounds) an object (or a set of objects) MBR f. p. : Every face of the MBR contains at least one point of some object in the database

Search improvement n Visit an MBR (node) only when necessary n How to do pruning? Using MINDIST and MINMAXDIST

MINDIST n n n MINDIST(P, R) is the minimum distance between a point P and a rectangle R If the point is inside R, then MINDIST=0 If P is outside of R, MINDIST is the distance of P to the closest point of R (one point of the perimeter)

MINDIST computation n MINDIST(p, R) is the minimum distance between p and R with corner points l and u n the closest point in R is at least this distance away R u=(u 1, u 2, …, ud) u p MINDIST = 0 ri = li if pi < li = ui if pi > ui = pi otherwise p l l=(l 1, l 2, …, ld) p

MINMAXDIST n n n MINMAXDIST(P, R): for each dimension, find the closest face, compute the distance to the furthest point on this face and take the minimum of all these (d) distances MINMAXDIST(P, R) is the smallest possible upper bound of distances from P to R MINMAXDIST guarantees that there is at least one object in R with a distance to P smaller or equal to it.

MINDIST and MINMAXDIST n MINDIST(P, R) <= NN(P) <=MINMAXDIST(P, R) R 1 MINMAXDIST R 4 R 3 MINDIST MINMAXDIST R 2 MINDIST

Pruning in NN search n n n Downward pruning: An MBR R is discarded if there exists another R’ s. t. MINDIST(P, R)>MINMAXDIST(P, R’) Downward pruning: An object O is discarded if there exists an R s. t. the Actual-Dist(P, O) > MINMAXDIST(P, R) Upward pruning: An MBR R is discarded if an object O is found s. t. the MINDIST(P, R) > Actual-Dist(P, O)

Pruning 1 example n Downward pruning: An MBR R is discarded if there exists another R’ s. t. MINDIST(P, R)>MINMAXDIST(P, R’) R R’ MINDIST MINMAXDIST

Pruning 2 example n Downward pruning: An object O is discarded if there exists an R s. t. the Actual-Dist(P, O) > MINMAXDIST(P, R) O R Actual-Dist MINMAXDIST

Pruning 3 example n Upward pruning: An MBR R is discarded if an object O is found s. t. the MINDIST(P, R) > Actual-Dist(P, O) R MINDIST Actual-Dist O

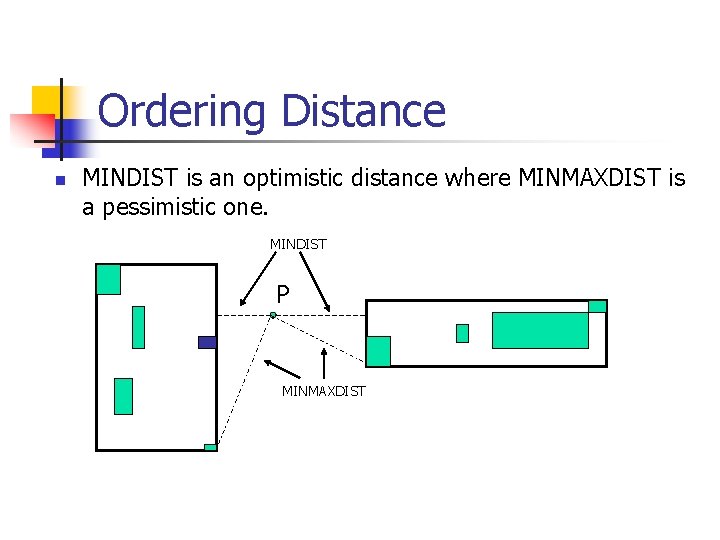
Ordering Distance n MINDIST is an optimistic distance where MINMAXDIST is a pessimistic one. MINDIST P MINMAXDIST

NN-search Algorithm 1. 2. 3. 4. 5. 6. 7. Initialize the nearest distance as infinite distance Traverse the tree depth-first starting from the root. At each Index node, sort all MBRs using an ordering metric and put them in an Active Branch List (ABL). Apply pruning rules 1 and 2 to ABL Visit the MBRs from the ABL following the order until it is empty If Leaf node, compute actual distances, compare with the best NN so far, update if necessary. At the return from the recursion, use pruning rule 3 When the ABL is empty, the NN search returns.

K-NN search n n Keep the sorted buffer of at most k current nearest neighbors Pruning is done using the k-th distance

Another NN search: Best-First n Global order [HS 99] n n n Maintain distance to all entries in a common Priority Queue Use only MINDIST Repeat n n n Inspect the next MBR in the list Add the children to the list and reorder Until all remaining MBRs can be pruned

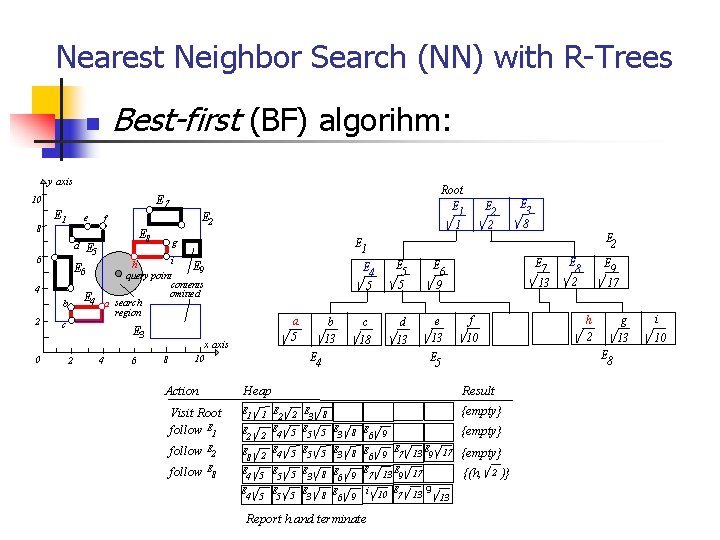
Nearest Neighbor Search (NN) with R-Trees Best-first (BF) algorihm: n y axis 8 E 1 e d 6 E 8 E 5 g i h E 9 query point contents omitted E 4 a search region b 0 E 2 f E 6 4 2 Root E 1 1 E 7 10 c E 3 2 4 6 a 5 x axis 8 follow E 6 9 c 18 d 13 e 13 E 2 E 8 E 1 2 E 2 E 4 8 E E 4 5 5 E 2 E 7 13 f 10 Report h and terminate {empty} 9 E 13 E 17 9 7 13 E 9 17 g 10 E 7 13 13 9 E 9 17 g 13 E 8 Result 2 E 3 8 5 E 5 5 E 3 8 E 6 9 E 7 5 E 3 8 E 6 9 i E 8 2 h 2 E 5 Heap Visit Root follow E 1 follow E 5 5 E 4 10 Action b 13 E 1 E 4 5 E 3 8 E 2 2 {empty} {(h, 2 )} i 10

HS algorithm Initialize PQ (priority queue) Inesrt. Queue(PQ, Root) While not Is. Empty(PQ) R= Dequeue(PQ) If R is an object Report R and exit (done!) If R is a leaf page node For each O in R, compute the Actual-Dists, Insert. Queue(PQ, O) If R is an index node For each MBR C, compute MINDIST, insert into PQ

Best-First vs Branch and Bound n n n Best-First is the “optimal” algorithm in the sense that it visits all the necessary nodes and nothing more! But needs to store a large Priority Queue in main memory. If PQ becomes large, we have thrashing… BB uses small Lists for each node. Also uses MINMAXDIST to prune some entries