SPATIAL EXTREMES AND SHAPES OF LARGE WAVES Herv

SPATIAL EXTREMES AND SHAPES OF LARGE WAVES Hervé Socquet-Juglard and Kristian B. Dysthe, Univ. of Bergen, Karsten Trulsen, Univ. of Oslo, Sébastien Fouques, Jingdong Liu, and Harald E. Krogstad, NTNU, Norway 1 ROGUE WAVES 2004 Workshop, Brest

• From one to two dimensions • Spatial measurements • Two tools: Piterbarg and Slepian • What do the simulations show? • Is the standard model good enough? 2 ROGUE WAVES 2004 Workshop, Brest

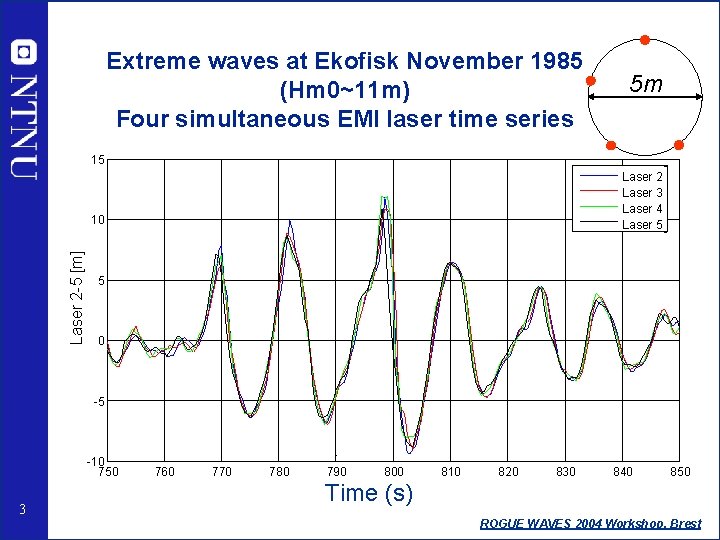
Extreme waves at Ekofisk November 1985 (Hm 0~11 m) Four simultaneous EMI laser time series 5 m 15 Laser 2 Laser 3 Laser 4 Laser 5 Laser 2 -5 [m] 10 5 0 -5 -10 750 3 760 770 780 790 800 810 820 830 840 850 Time (s) ROGUE WAVES 2004 Workshop, Brest

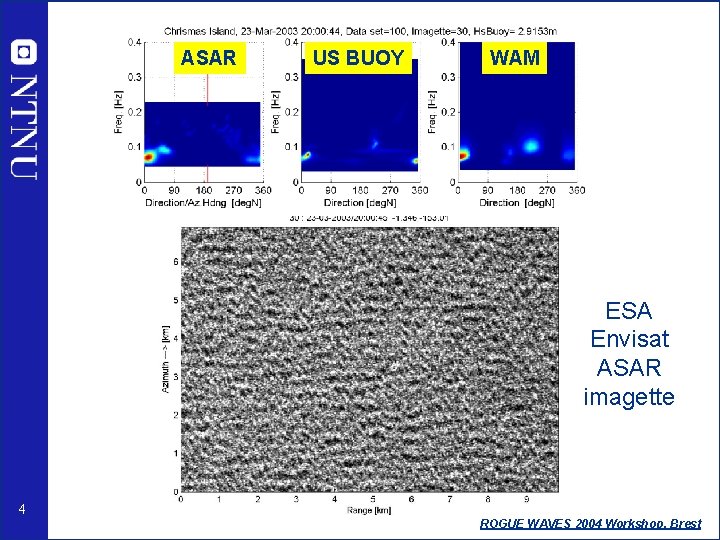
ASAR US BUOY WAM ESA Envisat ASAR imagette 4 ROGUE WAVES 2004 Workshop, Brest

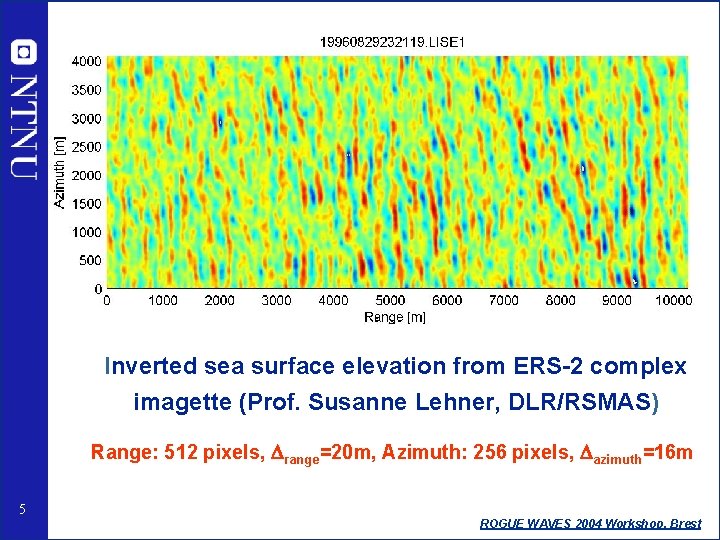
Inverted sea surface elevation from ERS-2 complex imagette (Prof. Susanne Lehner, DLR/RSMAS) Range: 512 pixels, Drange=20 m, Azimuth: 256 pixels, Dazimuth=16 m 5 ROGUE WAVES 2004 Workshop, Brest

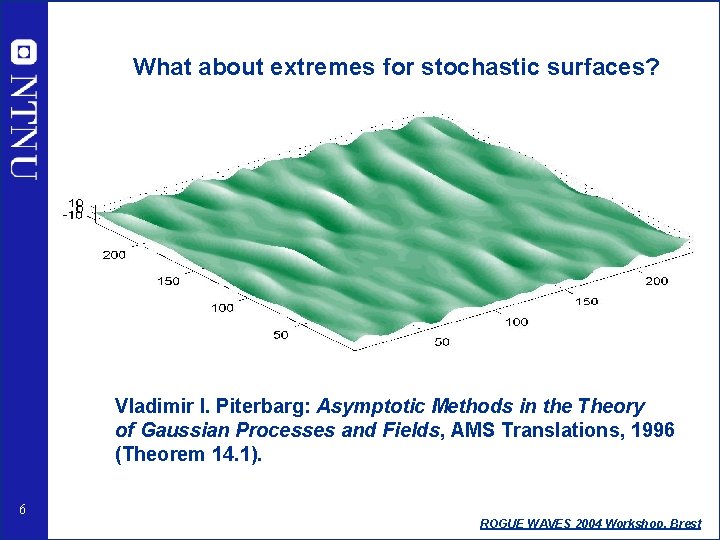
What about extremes for stochastic surfaces? Vladimir I. Piterbarg: Asymptotic Methods in the Theory of Gaussian Processes and Fields, AMS Translations, 1996 (Theorem 14. 1). 6 ROGUE WAVES 2004 Workshop, Brest

The 2 -D version of Piterbarg’s theorem: 7 ROGUE WAVES 2004 Workshop, Brest

• Piterbarg’s theorem settles the benchmark Gaussian case very nicely for all reasonably sized regions • The distribution depends only on the size of the region relative to the area of ”one wave” • The distribution converges to the Gumbel form when 8 ROGUE WAVES 2004 Workshop, Brest

Storm ”Gauss”: 100 x 100 km, Tz = 10 s, constant Hs, mean wave length = 250 m, mean crest length = 600 m, duration 6 hours: In time at a fixed location: In space at a fixed time: • N = 2100 • N = 6. 6 x 104 • E(max. Crest) = 1. 0 Hs • E(max. Crest) = 1. 3 Hs The total storm • N 2 x 107 • E(max. Crest)=1. 69 Hs Is a freak wave truly exceptional, or is it simply being at the wrong place at the wrong time? 9 ROGUE WAVES 2004 Workshop, Brest

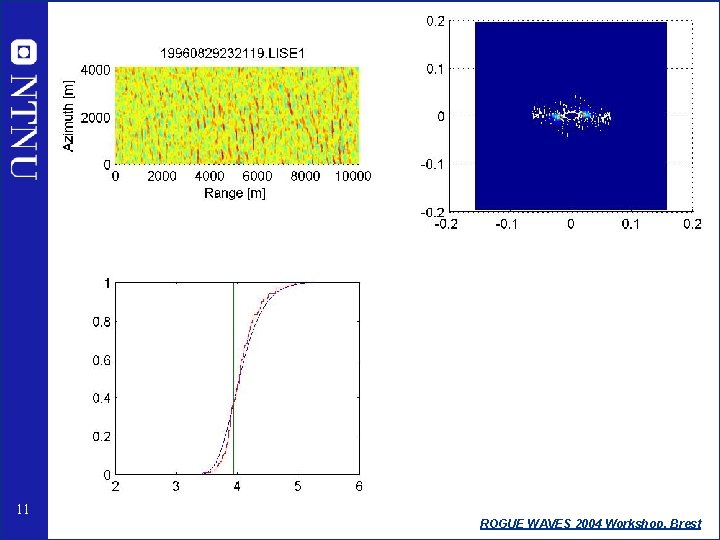
What about this one? 10 ROGUE WAVES 2004 Workshop, Brest

11 ROGUE WAVES 2004 Workshop, Brest

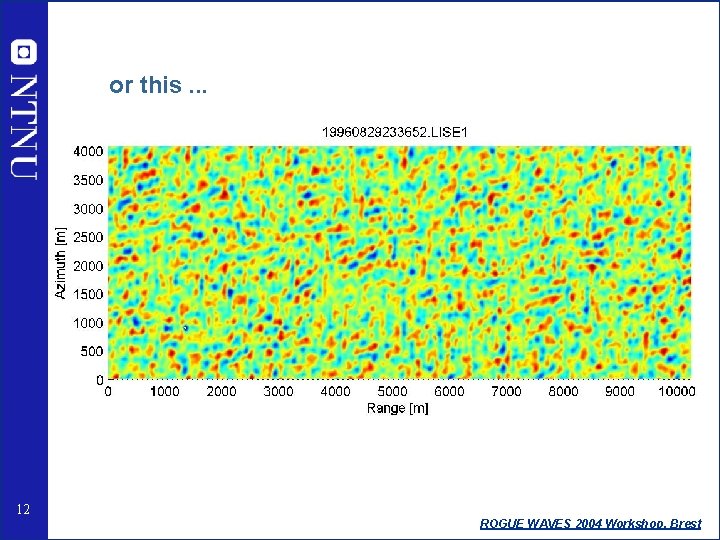
or this. . . 12 ROGUE WAVES 2004 Workshop, Brest

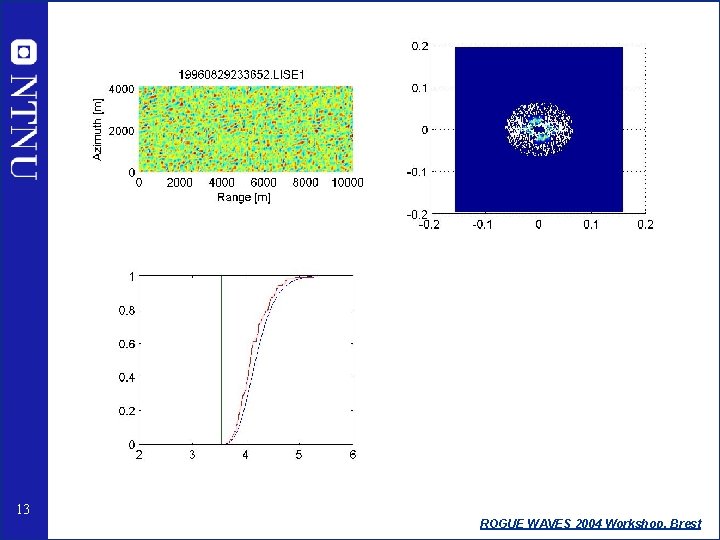
13 ROGUE WAVES 2004 Workshop, Brest

Small excerpts from simulated surfaces, 3 rd order reconstructions JONSWAP, narrow dir. distribution 14 JONSWAP, wider dir. distribution ROGUE WAVES 2004 Workshop, Brest

THE SLEPIAN MODEL REPRESENTATION (Lindgren, 1972): The shape of a Gaussian stochastic surface around a point • Optimal predictor (conditional expectation) in the Gaussian case • Optimal second order predictor in general 15 ROGUE WAVES 2004 Workshop, Brest

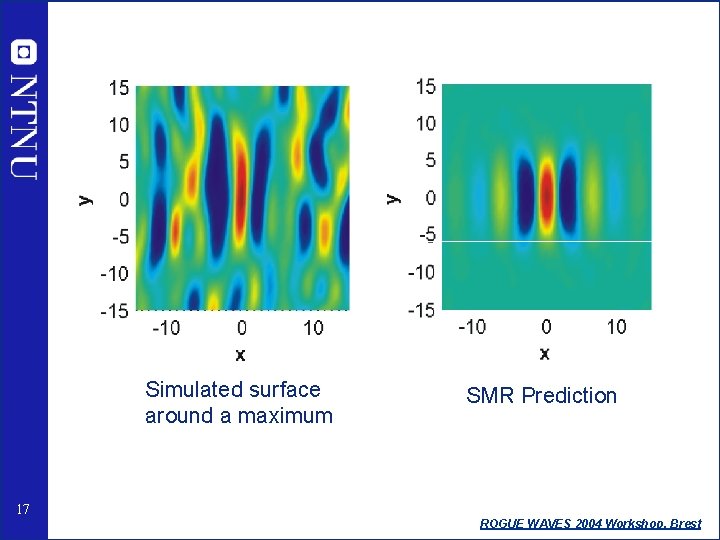
Around a high maximum: 16 ROGUE WAVES 2004 Workshop, Brest

Simulated surface around a maximum 17 SMR Prediction ROGUE WAVES 2004 Workshop, Brest

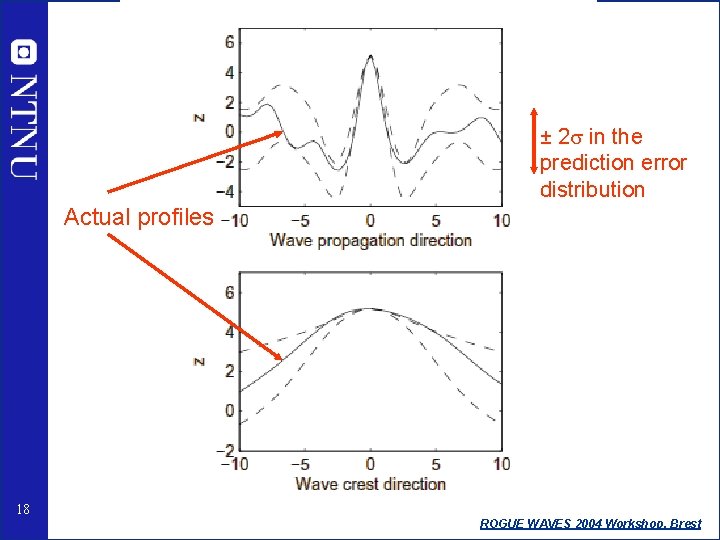
± 2 s in the prediction error distribution Actual profiles 18 ROGUE WAVES 2004 Workshop, Brest

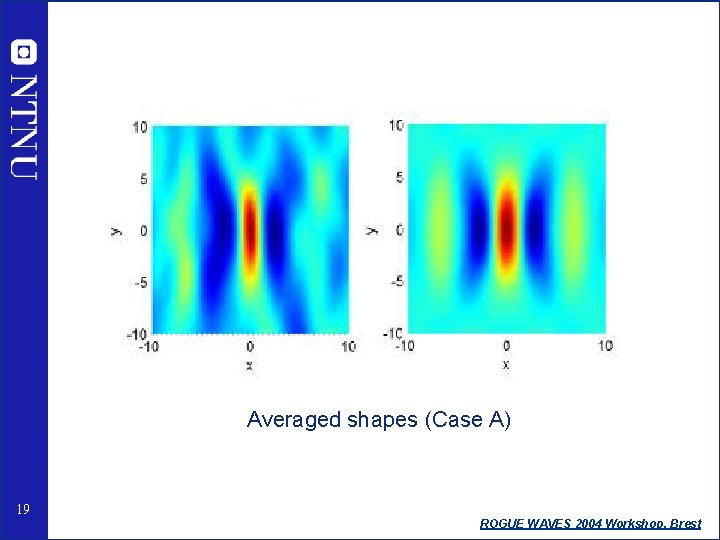
Averaged shapes (Case A) 19 ROGUE WAVES 2004 Workshop, Brest

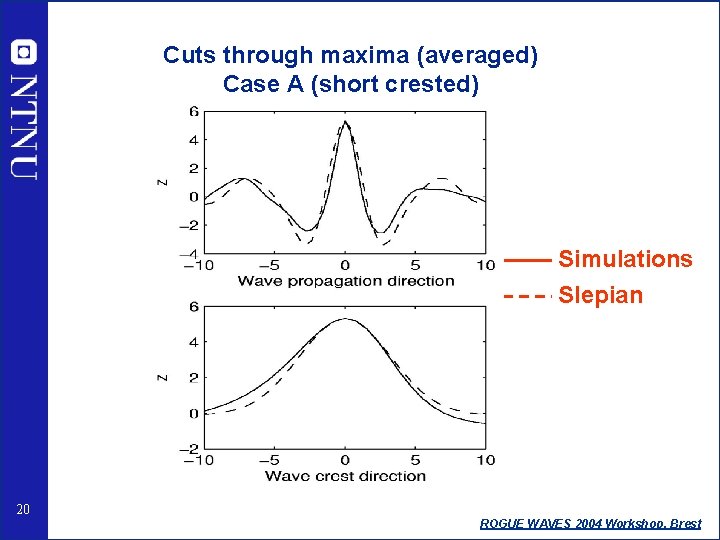
Cuts through maxima (averaged) Case A (short crested) Simulations Slepian 20 ROGUE WAVES 2004 Workshop, Brest

Cuts through maxima (averaged) Case B (long crested) Simulations Slepian 21 ROGUE WAVES 2004 Workshop, Brest

THE SHAPE OF MAXIMA: • The Slepian model prediction is only useful within a rather small neighbourhood about the maximum • Third order reconstructed waves are significantly steeper along the wave propagation direction than first order waves • Wave crests are in general a little longer than predicted by Gaussian theory, but appear to be bent in various directions, so that averages orthogonal to the wave propagation is similar 22 ROGUE WAVES 2004 Workshop, Brest

THE ”STANDARD MODEL”: • Eulerian based perturbation expansion • Linear Wave Theory is the leading order term 23 ROGUE WAVES 2004 Workshop, Brest

LAGRANGIAN MODELS: A DIFFERENT VIEW Eulerian: Velocity and pressure fields at fixed locations. Lagrangian: Track the motion of each particle as a function of time. Objective of our study: Investigate geometric and kinematic properties of a Lagrangian sea surface model for applications to radar backscatter. Lagrange, 1788; Gerstner, 1802; Lamb, 1932; Miche, 1942; Pohle (student of Stoker), 1950; Pierson, 1961, 1962; Chang, 1969; Gjøsund, Arntsen and Moe, 2002, and many more. . . 24 ROGUE WAVES 2004 Workshop, Brest

Variables: Mass conservation: (Integrated, 0 vorticity) Momentum conservation: Boundary conditions at the surface, d = 0, p=0 Boundary condition at the bottom: zt = 0 for d = -h 25 ROGUE WAVES 2004 Workshop, Brest

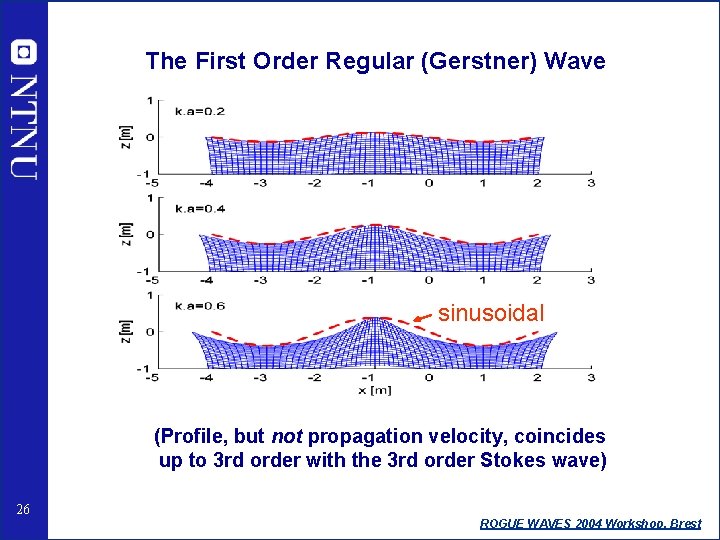
The First Order Regular (Gerstner) Wave sinusoidal (Profile, but not propagation velocity, coincides up to 3 rd order with the 3 rd order Stokes wave) 26 ROGUE WAVES 2004 Workshop, Brest

First order solution for a short wave riding on a long wave: 27 ROGUE WAVES 2004 Workshop, Brest

FIRST ORDER LAGRANGIAN MODEL: • Resembles Linear Wave Theory • No Stokes drift • The (Lagrangian) spectrum on the usual dispersion surface THE SECOND ORDER LAGRANGIAN MODEL • Needs integrated momentum equations as a basis • Uses particle velocity as the basic quantity (since Stokes drift prevents the use of particle position) 28 ROGUE WAVES 2004 Workshop, Brest

REAL WAVES peaked crests - rounded troughs 29 ROGUE WAVES 2004 Workshop, Brest

Excerpt of a simulation of 3 D first order Lagrangian waves 30 ROGUE WAVES 2004 Workshop, Brest

First order solutions 31 ROGUE WAVES 2004 Workshop, Brest

Second order solutions 32 ROGUE WAVES 2004 Workshop, Brest

ANIMATION OF 1 -D, SECOND ORDER LAGRANGIAN SOLUTION Note slow (Stokes) drift 33 ROGUE WAVES 2004 Workshop, Brest

CONCLUSIONS • Spatial data need spatial tools • Gaussian theory is still a benchmark case for random waves • Difficult verification of results and claims • Lagrangian model may show new features also relevant for extreme waves 34 ROGUE WAVES 2004 Workshop, Brest