Spatial Econometric Analysis Using GAUSS 1 KuanPin Lin

Spatial Econometric Analysis Using GAUSS 1 Kuan-Pin Lin Portland State University

Introduction to Spatial Econometric Analysis l Spatial Data l l l Cross Section Panel Data Spatial Dependence l l Spatial Heterogeneity Spatial Autocorrelation

Spatial Dependence l Least Squares Estimator

Spatial Dependence Nonparametric Treatment l Robust Inference l Spatial Heteroscedasticity Autocorrelation Variance-Covariance Matrix

Spatial Dependence Nonparametric Treatment l SHAC Estimator l l Kernel Function Normalized Distance

Spatial Dependence Parametric Representation l Spatial Weights Matrix l l Spatial Contiguity Geographical Distance § l First Law of Geography: Everything is related to everything else, but near things are more related than distant things. K-Nearest Neighbors

Spatial Dependence Parametric Representation l Characteristics of Spatial Weights Matrix l l Sparseness Weights Distribution Eigenvalues Higher-Order of Spatial Weights Matrix l l l W 2, W 3, … Redundandency Circularity

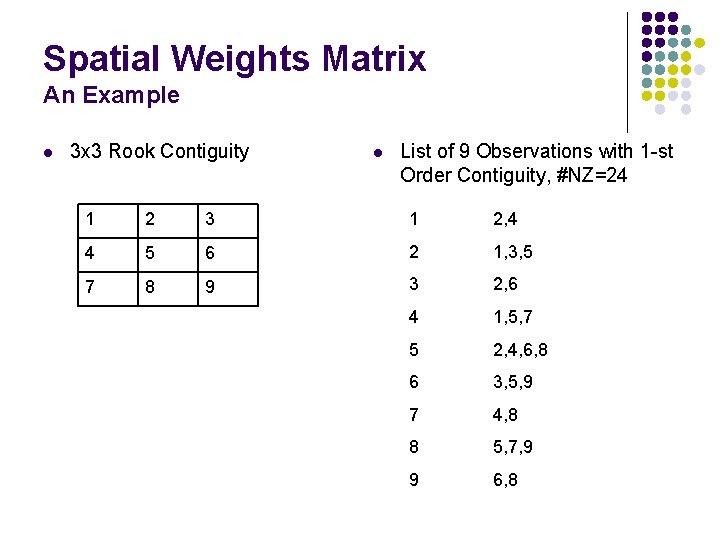
Spatial Weights Matrix An Example l 3 x 3 Rook Contiguity l List of 9 Observations with 1 -st Order Contiguity, #NZ=24 1 2 3 1 2, 4 4 5 6 2 1, 3, 5 7 8 9 3 2, 6 4 1, 5, 7 5 2, 4, 6, 8 6 3, 5, 9 7 4, 8 8 5, 7, 9 9 6, 8

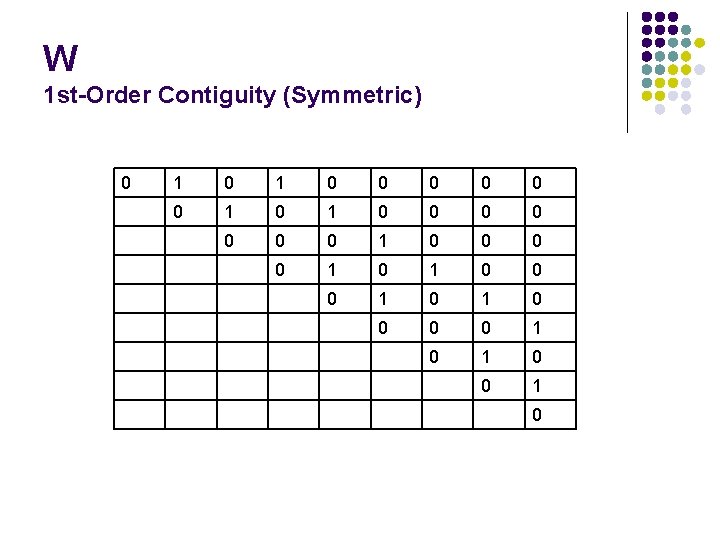
W 1 st-Order Contiguity (Symmetric) 0 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0

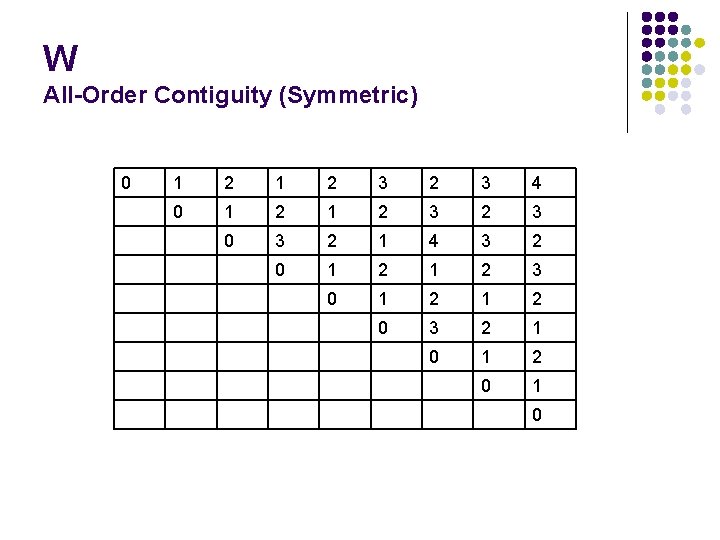
W All-Order Contiguity (Symmetric) 0 1 2 3 2 3 4 0 1 2 3 2 3 0 3 2 1 4 3 2 0 1 2 3 0 1 2 0 3 2 1 0 1 2 0 1 0

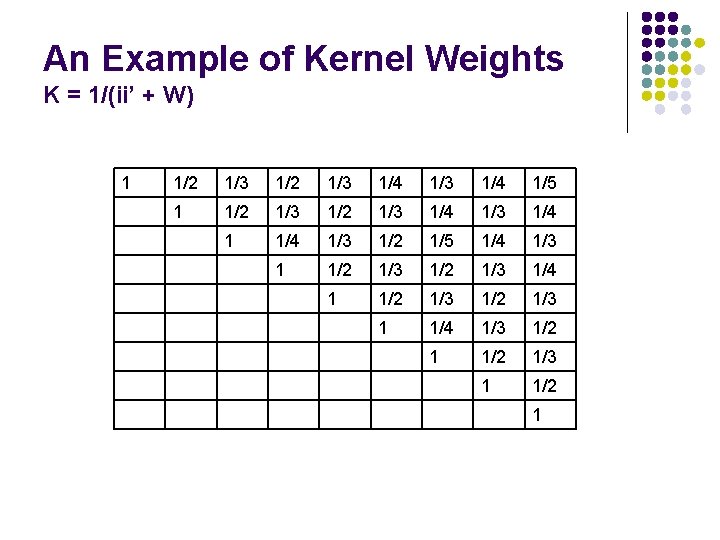
An Example of Kernel Weights K = 1/(ii’ + W) 1 1/2 1/3 1/4 1/5 1 1/2 1/3 1/4 1/3 1/2 1/5 1/4 1/3 1 1/2 1/3 1/4 1 1/2 1/3 1 1/4 1/3 1/2 1/3 1 1/2 1

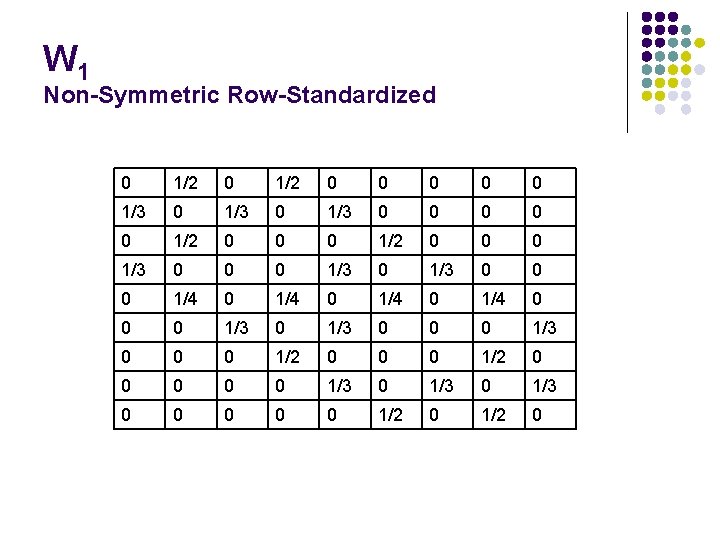
W 1 Non-Symmetric Row-Standardized 0 1/2 0 0 0 1/3 0 0 0 1/2 0 0 0 1/3 0 0 0 1/4 0 0 0 1/3 0 0 0 1/2 0 0 0 1/3 0 0 0 1/2 0

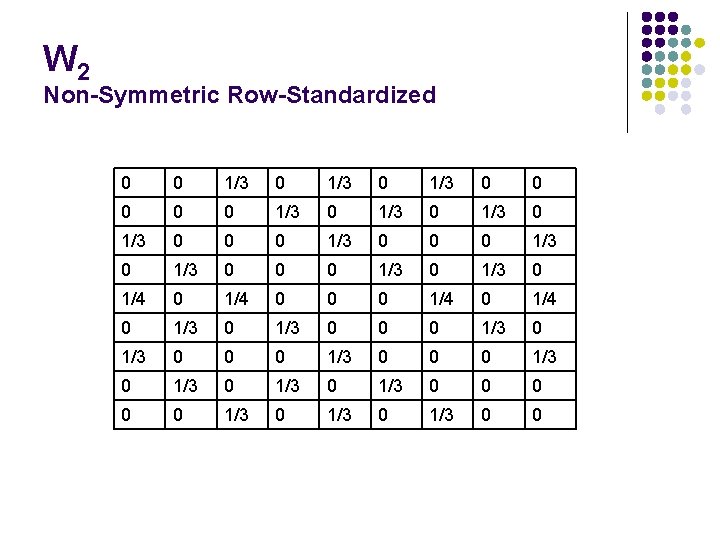
W 2 Non-Symmetric Row-Standardized 0 0 1/3 0 1/3 0 0 0 1/3 0 0 0 1/3 0 1/4 0 0 0 1/4 0 1/3 0 0 0 1/3 0 1/3 0 0 0 1/3 0 0

U. S. States

China Provinces

Spatial Lag Variables l l l Spatial Independent Variables Spatial Dependent Variables Spatial Error Variables

Spatial Econometric Models l Linear Regression Model with Spatial Variables l l l Spatial Lag Model Spatial Mixed Model Spatial Error Model

Examples l Anselin (1988): Crime Equation l Basic Model (Crime Rate) = a + b (Family Income) + g (Housing Value) + e l Spatial Lag Model (Crime Rate) = a + b (Family Income) + g (Housing Value) + l W (Crime Rate) + e l Spatial Error Model (Crime Rate) = e = r We + u l a + b (Family Income) + g (Housing Value) + e Data (anselin. txt, anselin_w. txt)

Examples l China Provincial GDP Output Function l Basic Model ln(GDP) = a + b ln(L) + g ln(K) + e l Spatial Mixed Model ln(GDP) = a + b ln(L) + g ln(K) + bw W ln(L) + gw W ln(K) + l W ln(GDP) + e l Data (china_gdp. txt, china_l. txt, china_k. txt, china_w. txt)

Examples l Ertur and Kosh (2007): International Technological Interdependence and Spatial Externalities l l 91 countries, growth convergence in 36 years (1960 -1995) Spatial Lag Solow Growth Model ln(y(t)) - ln(y(0)) = a + b ln(y(0)) + g ln(s) + g ln(n+g+d) + l W ln(y(t)) - ln(y(0))) + e l Data (data-ek. txt)

References l l l l L. Anselin, Spatial Econometrics: Methods and Models. Kluwer Academic Publishers, Boston, 1988. L. Anselin. “Spatial Econometrics, ” In T. C. Mills and K. Patterson (Eds. ), Palgrave Handbook of Econometrics: Volume 1, Econometric Theory. Basingstoke, Palgrave Macmillan, 2006: 901 -969. L. Anselin, “Under the Hood: Issues in the Specification and Interpretation of Spatial Regression Models, ” Agricultural Economics 17 (3), 2002: 247 -267. T. G. Conley, “Spatial Econometrics” Entry for New Palgrave Dictionary of Economics, 2 nd Edition, S Durlauf and L Blume, eds. (May 2008). C. Ertur and W. Kosh, “Growth, Technological Interdependence, Spatial Externalities: Theory and Evidence, ” Journal of Econometrics, 2007. J. Le. Sage and R. K. Pace, Introduction to Spatial Econometrics, Chapman & Hall, CRC Press, 2009. H. Kelejian and I. R. Prucha, “HAC Estimation in a Spatial Framework, ” Journal of Econometrics, 140: 131 -154.