Sparse Modeling of GraphStructured Data and Images Michael

Sparse Modeling of Graph-Structured Data … and … Images Michael Elad The Computer Science Department The Technion The research leading to these results has been received funding from the European union's Seventh Framework Programme 1 (FP/2007 -2013) ERC grant Agreement ERC-SPARSE- 320649

SPARSITY: What is it Good For? This part relies on the following two papers: q M. Elad, Sparse and Redundant Representation Modeling — What Next? , IEEE Signal Processing Letters, Vol. 19, No. 12, Pages 922 -928, December 2012. q A. M. Bruckstein, D. L. Donoho, and M. Elad, From Sparse Solutions of Systems of Equations to Sparse Modeling of Signals and Images, SIAM Review, Vol. 51, No. 1, Pages 34 -81, February 2009. Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 2

Good News Today, we have the technology and the know-how to effectively process data Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 3

Which Data? Stock Market Biological Signals Still Images Social Networks Matrix Data Videos Text Documents Voice Signals Traffic info Medical Imaging Seismic Data Radar Imaging Email Traffic Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 3 D Objects 4

What Processing? What can we do for such signals? q q q q q Denoising – removal of noise from the data Interpolation (inpainting) – recovery of missing values Prediction – extrapolating the data beyond the given domain Compression – reduction of storage and transmission volumes Inference (inverse problems) – recovery from corrupted measurements Separation – breaking down a data to its morphological “ingredients” Anomaly detection – discovering outliers in the data Clustering – gathering subsets of closely related instances within the data Summarizing – creating a brief version of the essence of the data Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 5

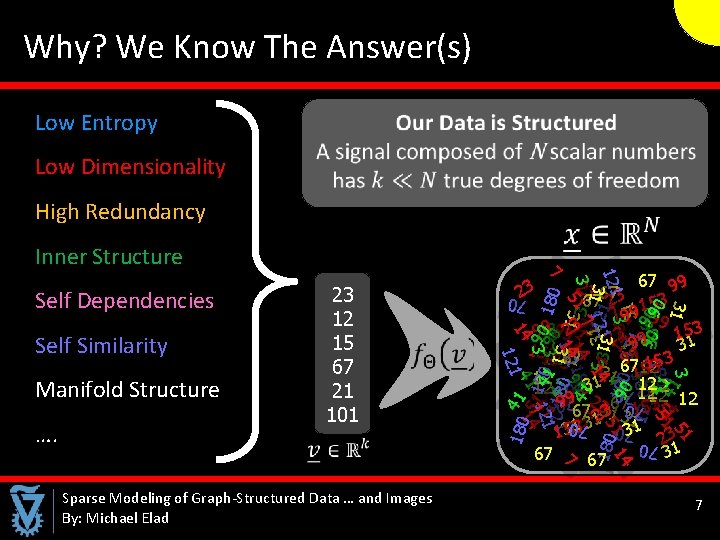
So, Here is a Simple Question Why all This is Possible? q Is it obvious that all these processing options should be possible? q Consider the following data source: Many of the processing tasks mentioned above are impossible for this data q Is there something common to all the above-mentioned signals, that makes them “processable”? Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 6

Why? We Know The Answer(s) Low Entropy Low Dimensionality High Redundancy Inner Structure 180 41 51 1 4810 990 1 0 80 14810 51 41 3 14 31 2 180 3 1 1 91080 1 4 51 3211 31 121 930 909 41 0 14 41 Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 7700 70 70 …. 23 12 15 67 21 101 70 70 Manifold Structure 23 70 Self Similarity 23 67 67 99 67 23 153 7 99 99 7 2 999923 3 23 9 153 9 31 1513 99 9 12 5367 9 12 1353 67 5 3 1 12 1 1 7 1212 3 12 7 1 99 2 67 1212 12 7 7 53 67 32331 311537 1 31 3 13513 3 2 31 67 7 67 3 3 51 1 11 180 55 90 14810 3 1 51 14 1231 2131 44 1 31 1 4 0 3 13 51 3 5 1 124111890 1 1 3 1 121 90 3 121 3 1 14 14 214 1 Self Dependencies 7 7

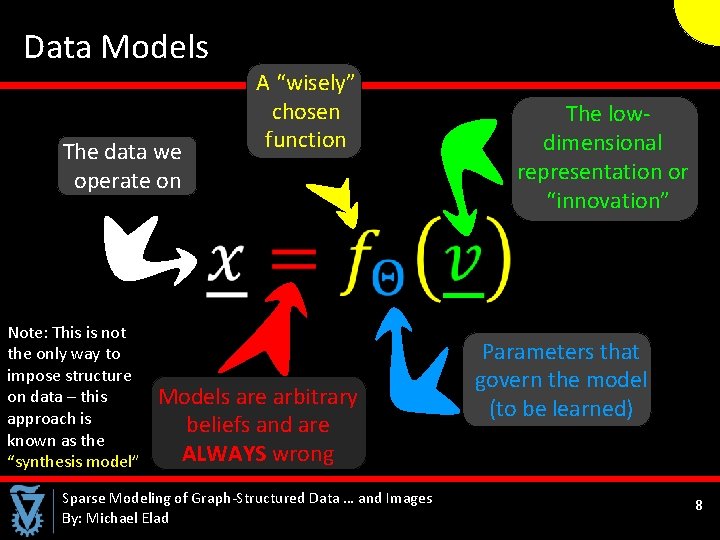
Data Models The data we operate on A “wisely” chosen function The lowdimensional representation or “innovation” Note: This is not the only way to impose structure on data – this approach is known as the “synthesis model” Models are arbitrary beliefs and are ALWAYS wrong Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad Parameters that govern the model (to be learned) 8

Processing Data Using Models Q: Why all This is Possible? Processing signals (denoise, interpolate, predict, compress, infer, separate, detect, cluster, summarize, …) A: Because of the structure! Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 9

Processing Data Using Models Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 10

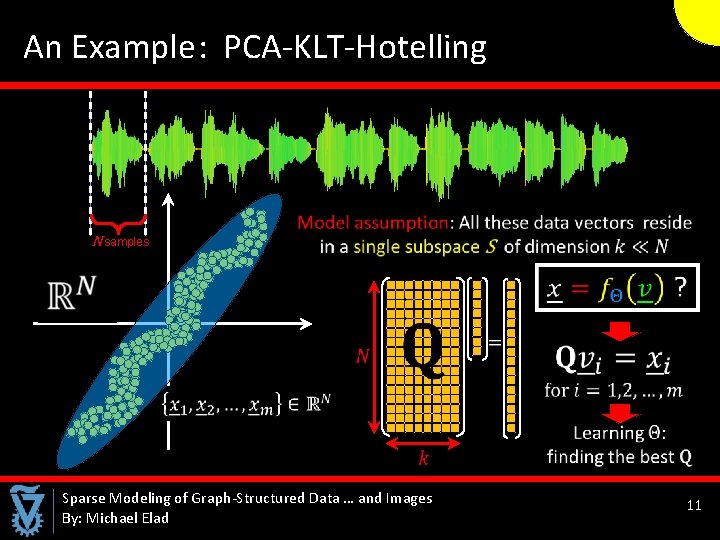
An Example : PCA-KLT-Hotelling N samples Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 11

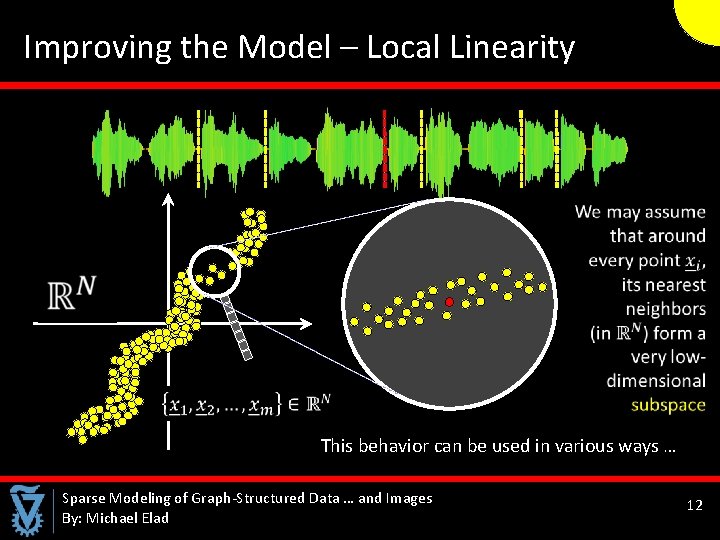
Improving the Model – Local Linearity This behavior can be used in various ways … Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 12

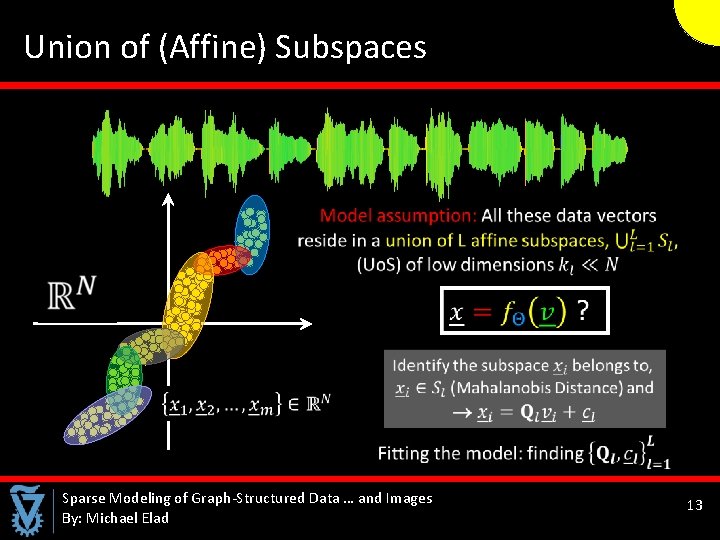
Union of (Affine) Subspaces Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 13

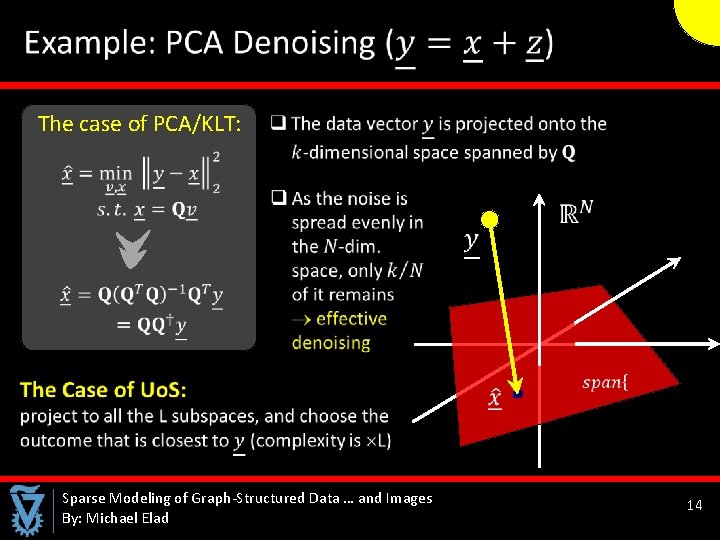
The case of PCA/KLT: Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 14

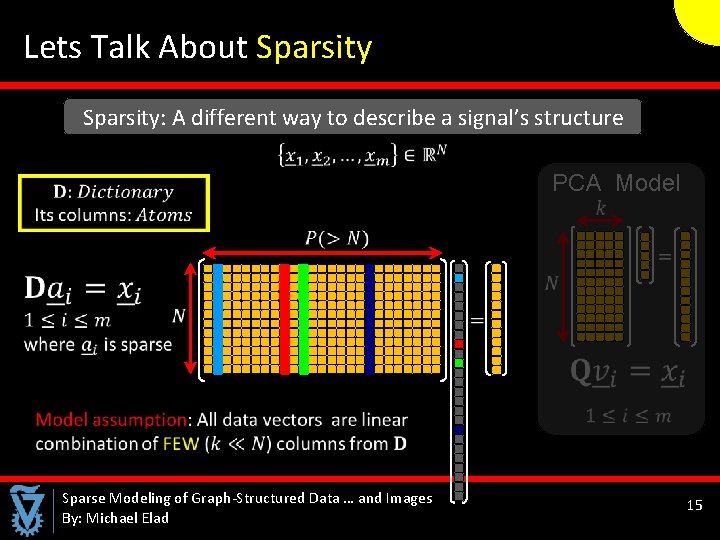
Lets Talk About Sparsity: A different way to describe a signal’s structure PCA Model Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 15

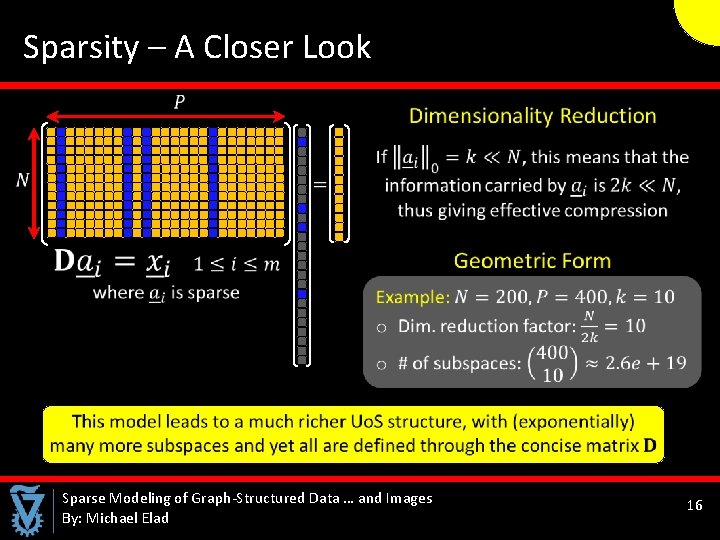
Sparsity – A Closer Look Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 16

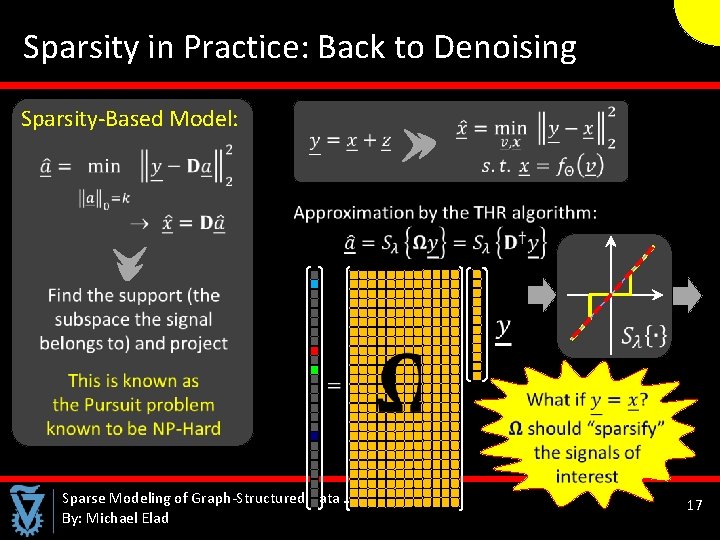
Sparsity in Practice: Back to Denoising Sparsity-Based Model: Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 17

To Summarize So Far Processing data is enabled by an appropriate modeling that exposes its inner structure Note: Our motivation is “image processing” Broadly speaking, an effective way to model data is via sparse representations We shall now turn to adopt this concept for nonconventional data structure - graph Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad This leads to a rich and highly effective and popular Unionof-Subspaces model 18

Processing GRAPH Structured Data Joint work with Idan Ram Israel Cohen The Electrical Engineering department Technion – Israel Institute of Technology This part relies on the following two papers: q I. Ram, M. Elad, and I. Cohen, “Generalized Tree-Based Wavelet Transform”, IEEE Trans. Signal Processing, vol. 59, no. 9, pp. 4199– 4209, 2011. q I. Ram, M. Elad, and I. Cohen, “Redundant Wavelets on Graphs and High Dimensional Data Clouds”, IEEE Signal Processing Letters, Vol. 19, No. 5, pp. 291– 294 , May 2012. Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 19

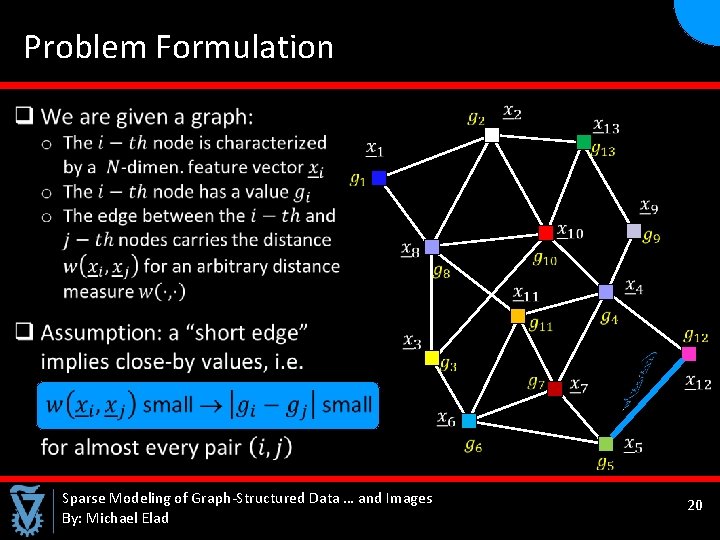
Problem Formulation Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 20

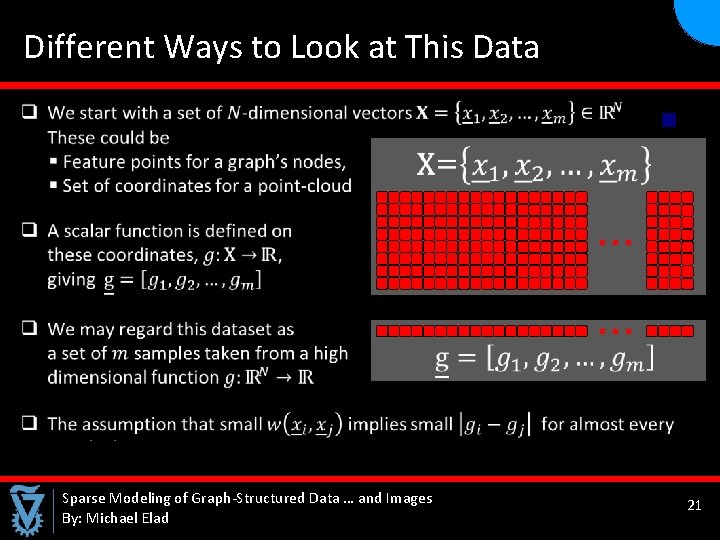
Different Ways to Look at This Data n … … Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 21

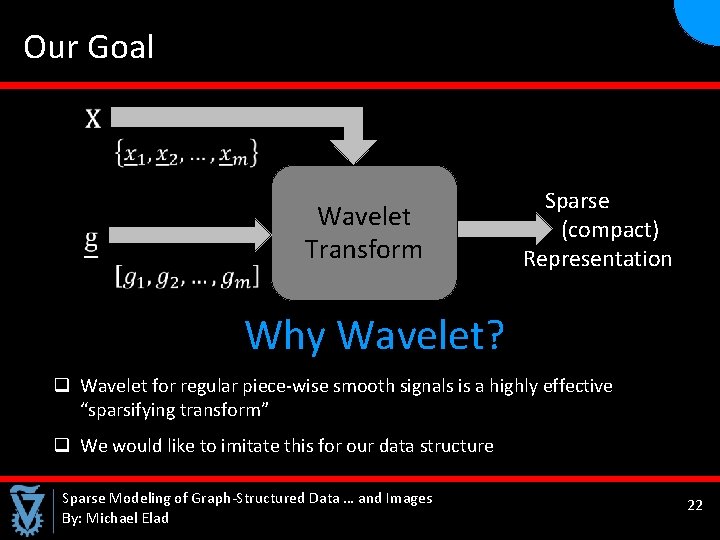
Our Goal Wavelet Transform Sparse (compact) Representation Why Wavelet? q Wavelet for regular piece-wise smooth signals is a highly effective “sparsifying transform” q We would like to imitate this for our data structure Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 22

Wavelet for Graphs – A Wonderful Idea I wish we would have thought of it first … “Diffusion Wavelets” R. R. Coifman, and M. Maggioni, 2006. “Multiscale Methods for Data on Graphs and Irregular Multidimensional Situations” M. Jansen, G. P. Nason, and B. W. Silverman, 2008. “Wavelets on Graph via Spectal Graph Theory” D. K. Hammond, and P. Vandergheynst, and R. Gribonval, 2010. “Multiscale Wavelets on Trees, Graphs and High Dimensional Data: Theory and Applications to Semi Supervised Learning” M. Gavish, and B. Nadler, and R. R. Coifman, 2010. “Wavelet Shrinkage on Paths for Denoising of Scattered Data” D. Heinen and G. Plonka, 2012 Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 23

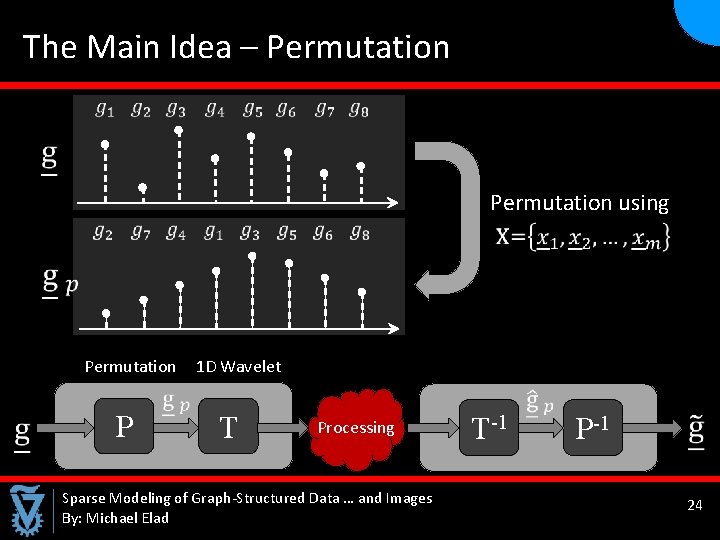
The Main Idea – Permutation Permutation P Permutation using 1 D Wavelet T Processing Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad T-1 P-1 24

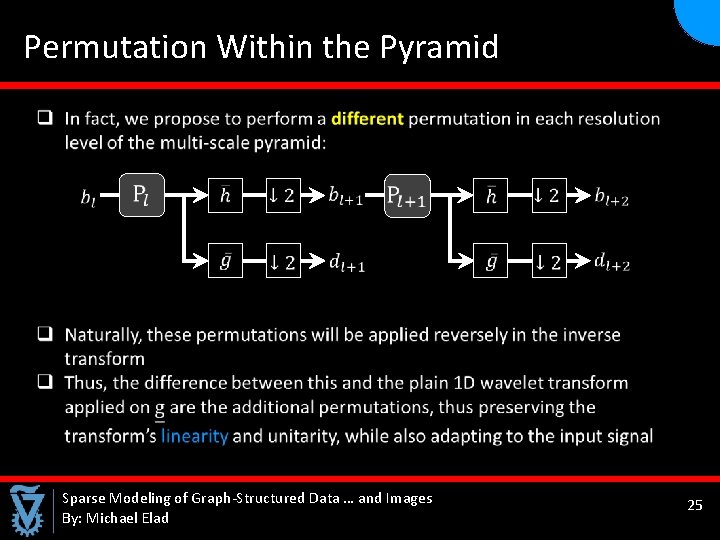
Permutation Within the Pyramid Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 25

Permute to Obtain Maximal Regularity Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 26

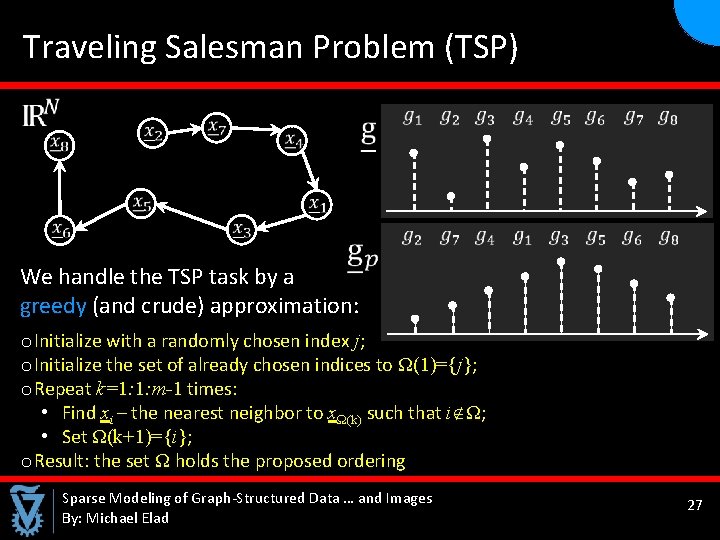
Traveling Salesman Problem (TSP) We handle the TSP task by a greedy (and crude) approximation: o Initialize with a randomly chosen index j; o Initialize the set of already chosen indices to Ω(1)={j}; o Repeat k=1: 1: m-1 times: • Find xi – the nearest neighbor to xΩ(k) such that i Ω; • Set Ω(k+1)={i}; o Result: the set Ω holds the proposed ordering Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 27

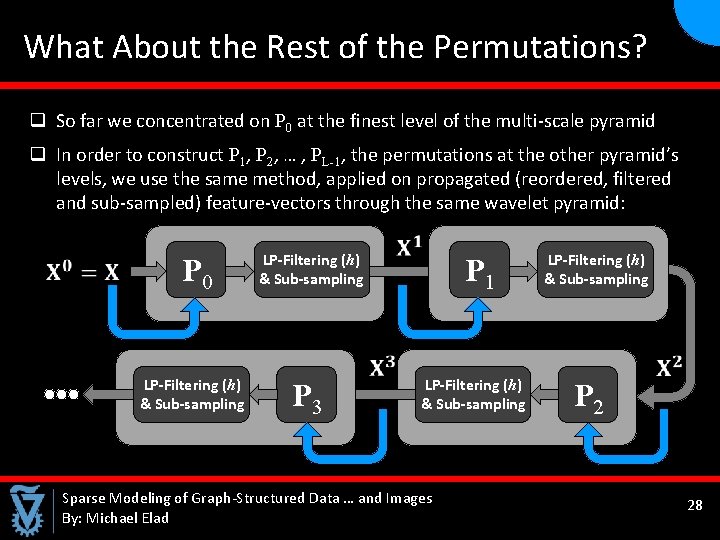
What About the Rest of the Permutations? q So far we concentrated on P 0 at the finest level of the multi-scale pyramid q In order to construct P 1, P 2, … , PL-1, the permutations at the other pyramid’s levels, we use the same method, applied on propagated (reordered, filtered and sub-sampled) feature-vectors through the same wavelet pyramid: P 0 LP-Filtering (h) & Sub-sampling P 3 P 1 LP-Filtering (h) & Sub-sampling Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad LP-Filtering (h) & Sub-sampling P 2 28

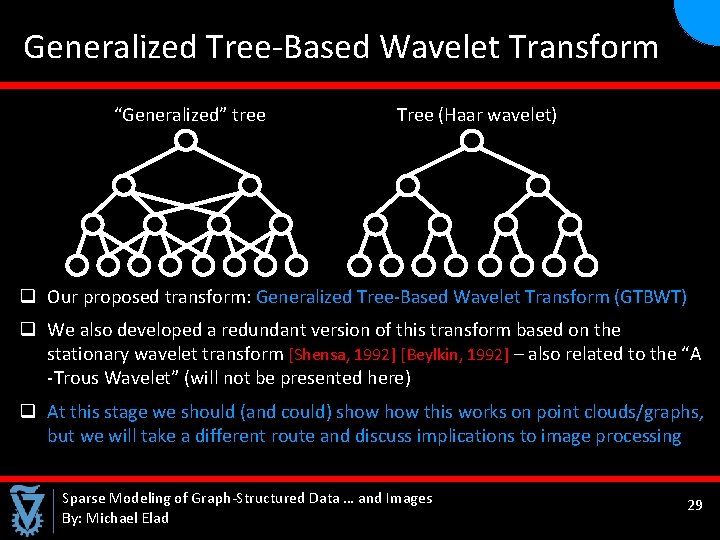
Generalized Tree-Based Wavelet Transform “Generalized” tree Tree (Haar wavelet) q Our proposed transform: Generalized Tree-Based Wavelet Transform (GTBWT) q We also developed a redundant version of this transform based on the stationary wavelet transform [Shensa, 1992] [Beylkin, 1992] – also related to the “A -Trous Wavelet” (will not be presented here) q At this stage we should (and could) show this works on point clouds/graphs, but we will take a different route and discuss implications to image processing Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 29

To Summarize So Far Given a graph or a cloud of points, we can model it in order to process it (denoise, infer, …) We shall present the applicability of this transform to … images The approach we take is to extend the existing 1 D wavelet transform to the graph structure We tested this for graph data with successful results (NOT SHOWN HERE) Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad Our method: Permutation followed by filtering and decimation in each of the pyramid levels 30

Turning to IMAGE PROCESSING This part relies on the same papers mentioned before … q I. Ram, M. Elad, and I. Cohen, “Generalized Tree-Based Wavelet Transform”, IEEE Trans. Signal Processing, vol. 59, no. 9, pp. 4199– 4209, 2011. q I. Ram, M. Elad, and I. Cohen, “Redundant Wavelets on Graphs and High Dimensional Data Clouds”, IEEE Signal Processing Letters, Vol. 19, No. 5, pp. 291– 294 , May 2012. Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 31

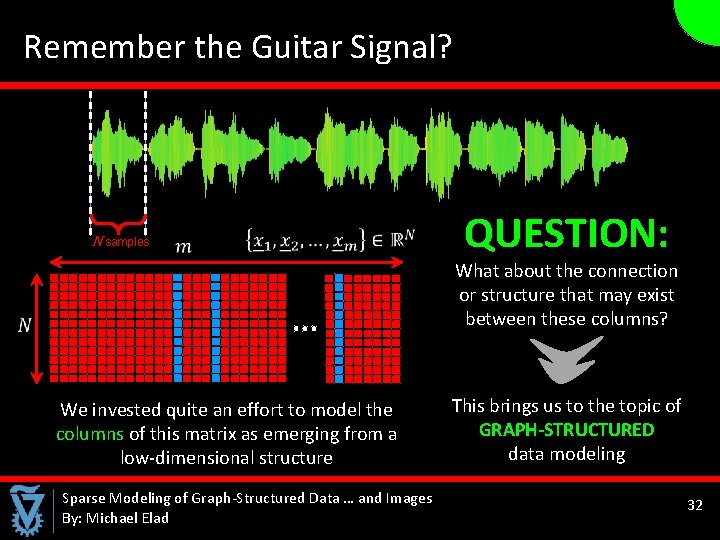
Remember the Guitar Signal? N samples We invested quite an effort to model the columns of this matrix as emerging from a low-dimensional structure Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad QUESTION: What about the connection or structure that may exist between these columns? This brings us to the topic of GRAPH-STRUCTURED data modeling 32

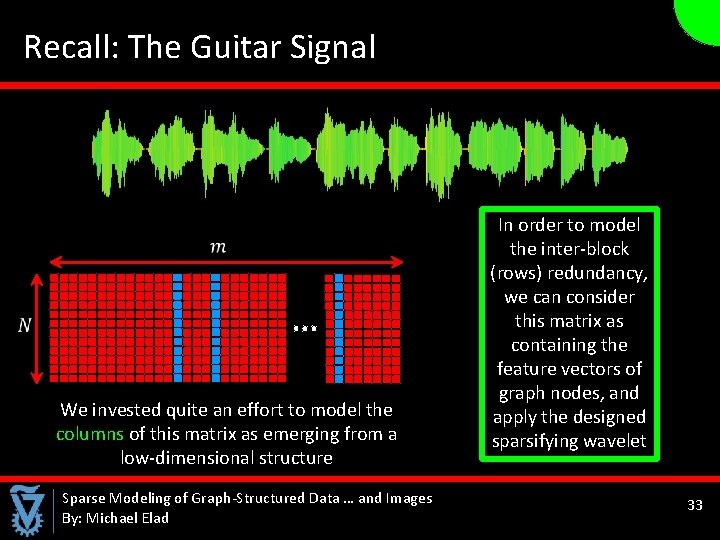
Recall: The Guitar Signal We invested quite an effort to model the columns of this matrix as emerging from a low-dimensional structure Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad In order to model the inter-block (rows) redundancy, we can consider this matrix as containing the feature vectors of graph nodes, and apply the designed sparsifying wavelet 33

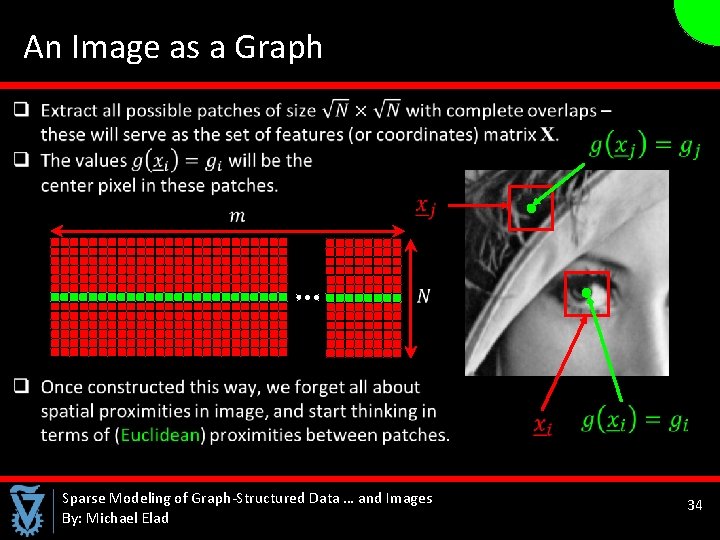
An Image as a Graph Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 34

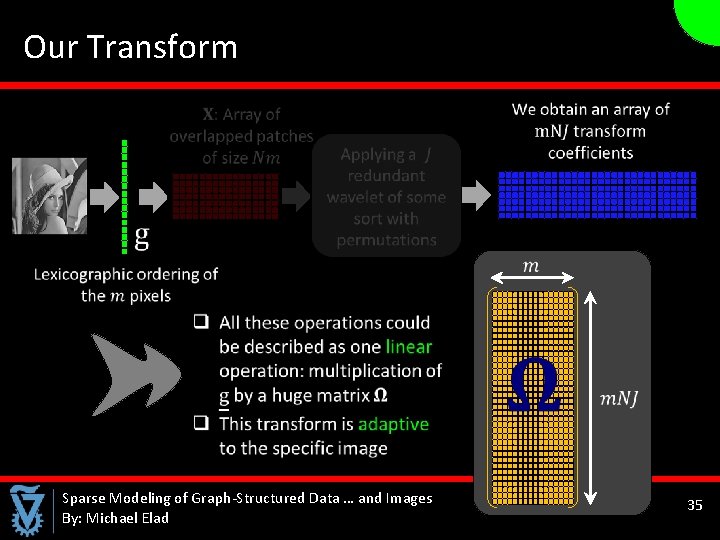
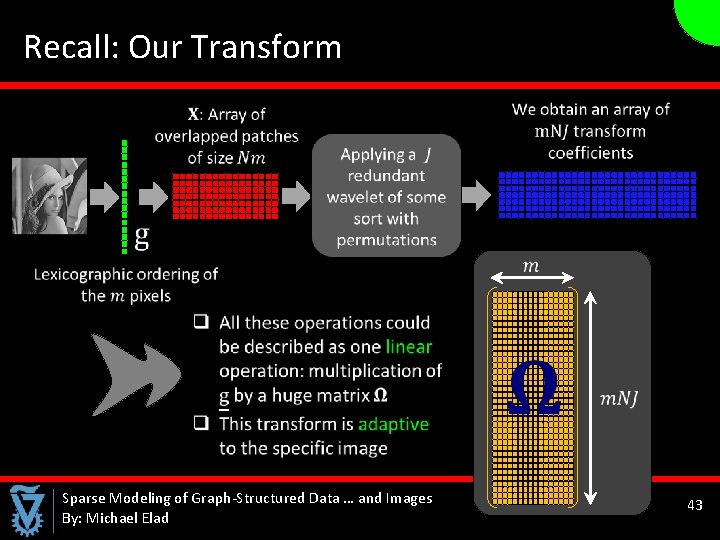
Our Transform Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 35

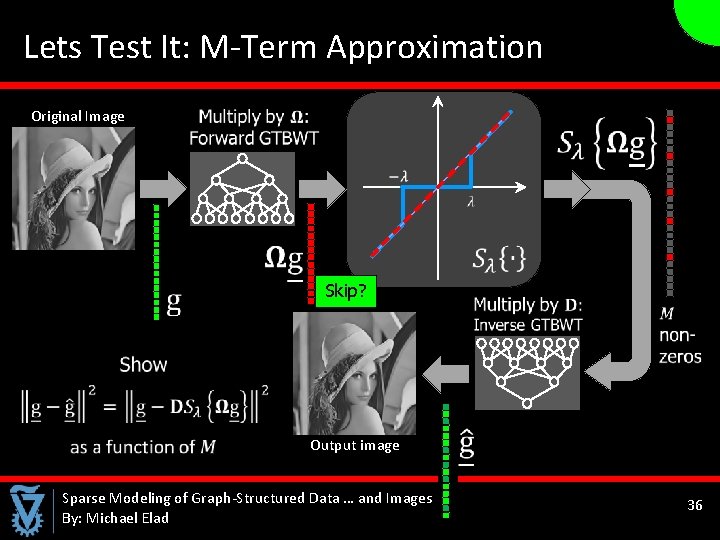
Lets Test It: M-Term Approximation Original Image Skip? Output image Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 36

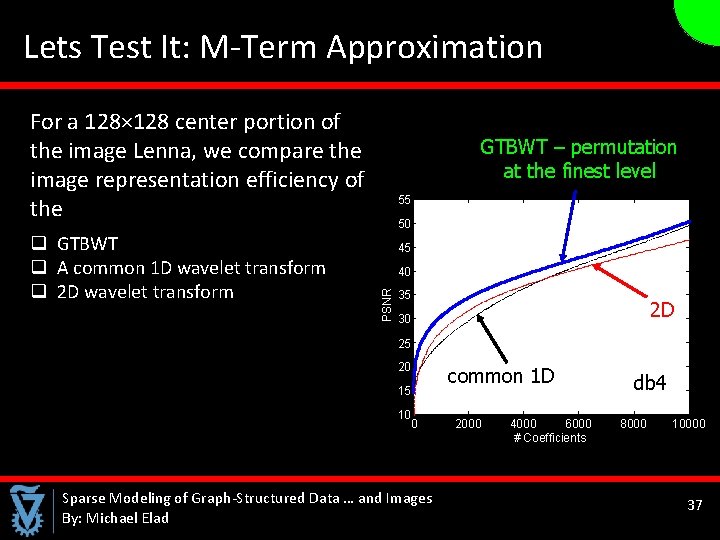
Lets Test It: M-Term Approximation For a 128× 128 center portion of the image Lenna, we compare the image representation efficiency of the GTBWT – permutation at the finest level 55 50 45 40 PSNR q GTBWT q A common 1 D wavelet transform q 2 D wavelet transform 35 2 D 30 25 20 15 10 0 Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad common 1 D 2000 4000 6000 # Coefficients db 4 8000 10000 37

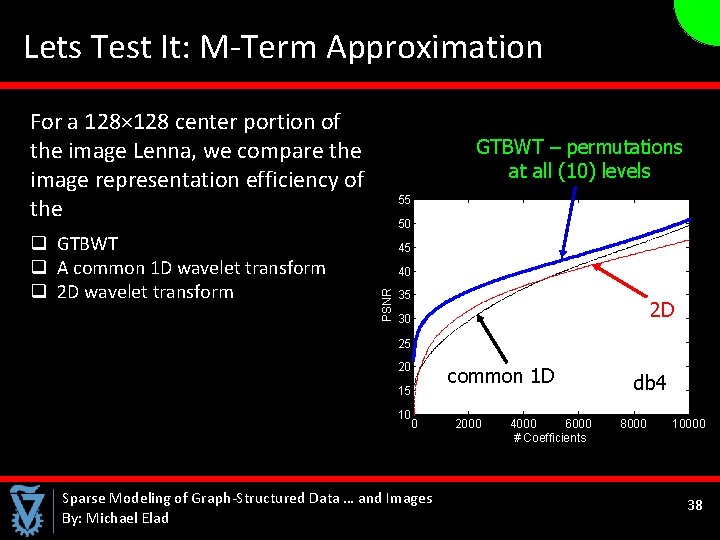
Lets Test It: M-Term Approximation For a 128× 128 center portion of the image Lenna, we compare the image representation efficiency of the GTBWT – permutations at all (10) levels 55 50 45 40 PSNR q GTBWT q A common 1 D wavelet transform q 2 D wavelet transform 35 2 D 30 25 20 15 10 0 Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad common 1 D 2000 4000 6000 # Coefficients db 4 8000 10000 38

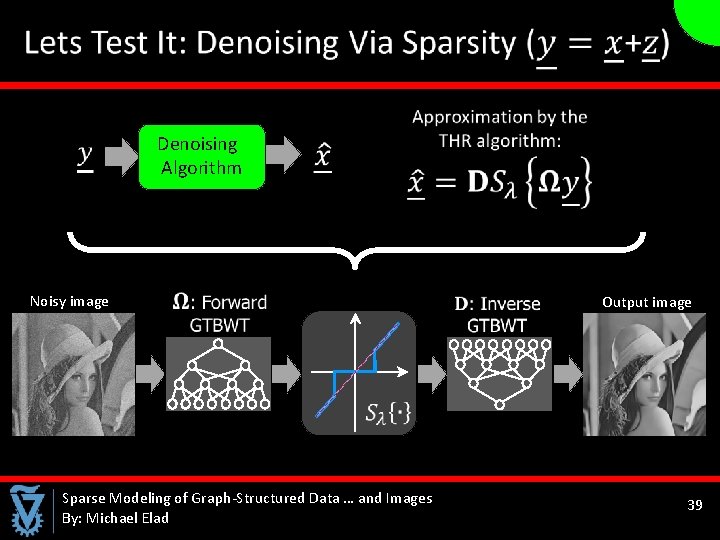
Noisy image Denoising Algorithm Output image Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 39

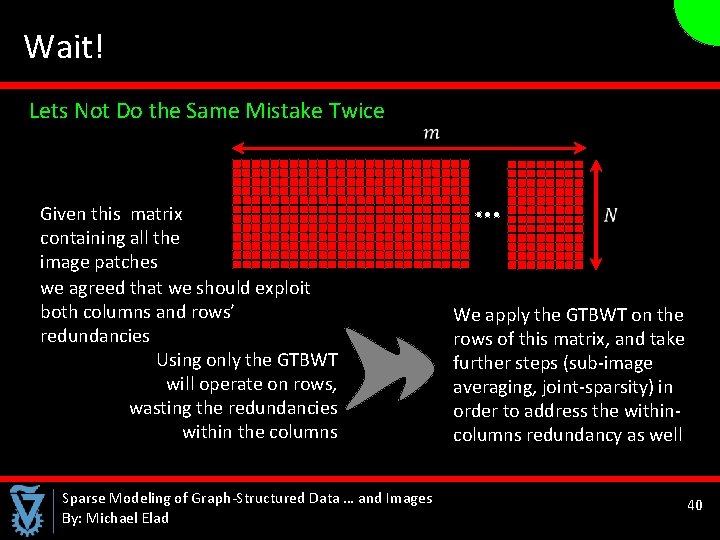
Wait! Lets Not Do the Same Mistake Twice Given this matrix containing all the image patches we agreed that we should exploit both columns and rows’ redundancies Using only the GTBWT will operate on rows, wasting the redundancies within the columns Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad We apply the GTBWT on the rows of this matrix, and take further steps (sub-image averaging, joint-sparsity) in order to address the withincolumns redundancy as well 40

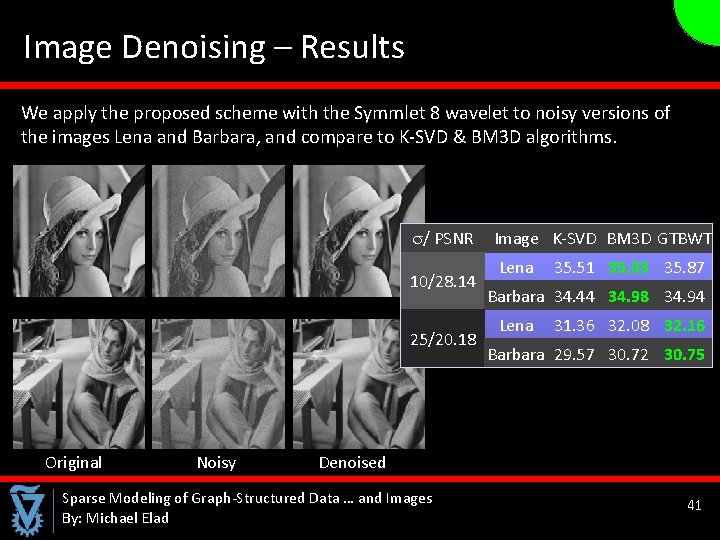
Image Denoising – Results We apply the proposed scheme with the Symmlet 8 wavelet to noisy versions of the images Lena and Barbara, and compare to K-SVD & BM 3 D algorithms. / PSNR 10/28. 14 25/20. 18 Image K-SVD BM 3 D GTBWT Lena 35. 51 35. 93 35. 87 Barbara 34. 44 34. 98 34. 94 Lena 31. 36 32. 08 32. 16 Barbara 29. 57 30. 72 30. 75 Original Noisy Denoised Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 41

What Next? A: Refer to this transform We have a highly effective sparsifying transform for images. It is “linear” and image adaptive Skip? as an abstract sparsification operator and use it in general image processing tasks B: Streep this idea to its bones: keep the patchreordering, and propose a new way to process images This part is based on the following papers: q I. Ram, M. Elad, and I. Cohen, “The RTBWT Frame – Theory and Use for Images”, working draft to be submitted soon. q I. Ram, M. Elad, and I. Cohen, “Image Processing using Smooth Ordering of its Patches”, to appear in IEEE Transactions on Image Processing. Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 42

Recall: Our Transform Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 43

Deblurring Anomaly Detection Separation Denoising Super. Resolution … Inpainting Sampling: Compressed -Sensing … Compression Tomographic Reconstruction Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 44

A: E. g. Deblurring Results Original Blurred Restored Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 45

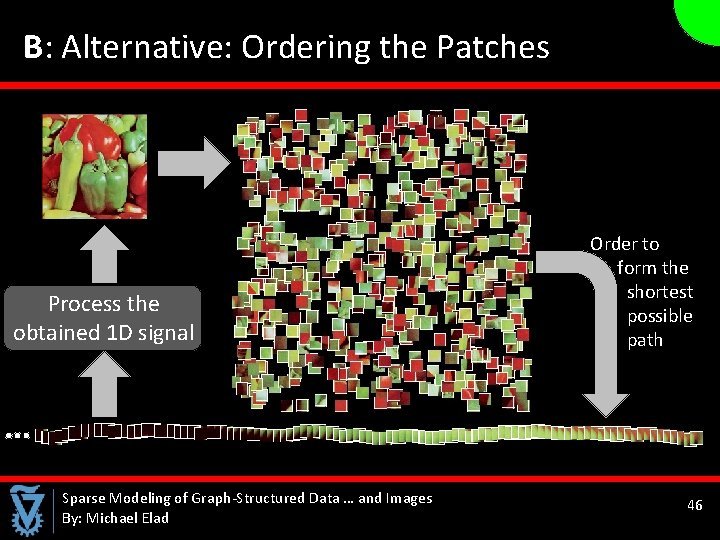
B: Alternative: Ordering the Patches Process the obtained 1 D signal Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad Order to form the shortest possible path 46 46

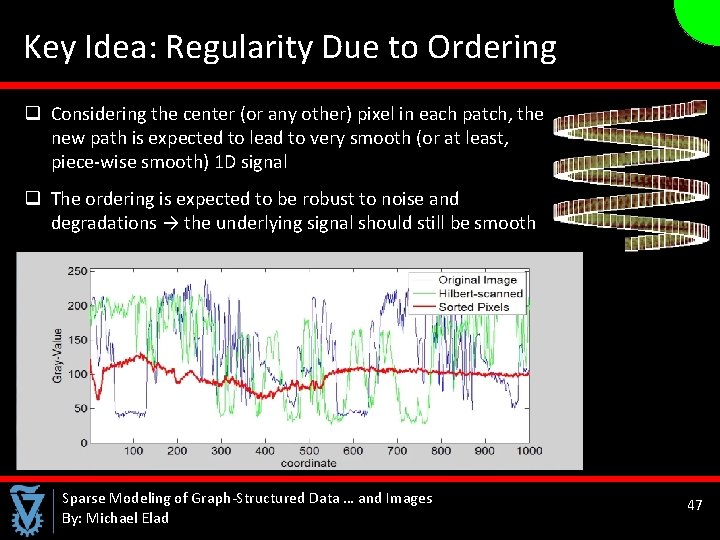
Key Idea: Regularity Due to Ordering q Considering the center (or any other) pixel in each patch, the new path is expected to lead to very smooth (or at least, piece-wise smooth) 1 D signal q The ordering is expected to be robust to noise and degradations → the underlying signal should still be smooth Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 47

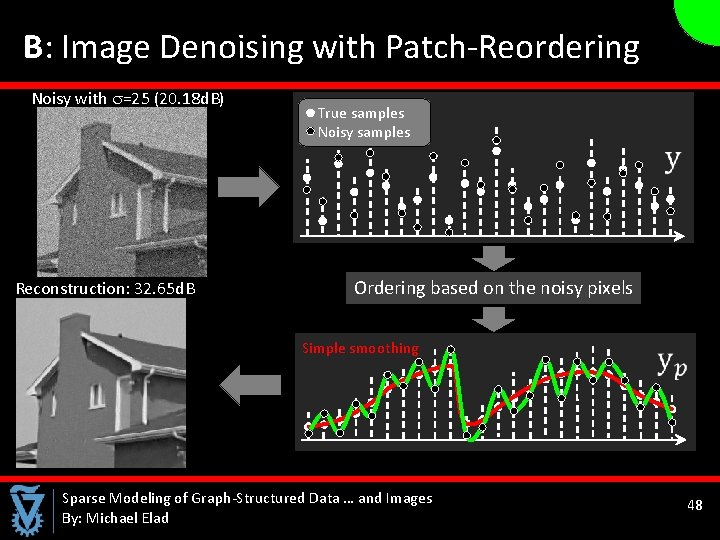
B: Image Denoising with Patch-Reordering Noisy with =25 (20. 18 d. B) Reconstruction: 32. 65 d. B True samples Noisy samples Ordering based on the noisy pixels Simple smoothing Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 48 48

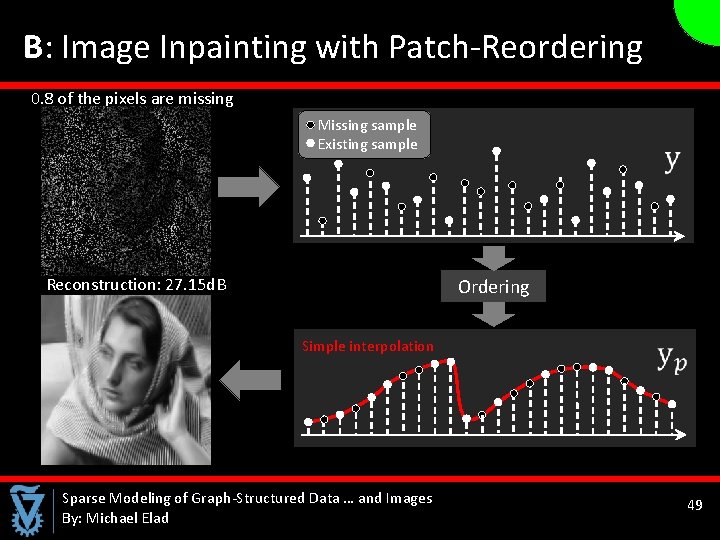
B: Image Inpainting with Patch-Reordering 0. 8 of the pixels are missing Missing sample Existing sample Reconstruction: 27. 15 d. B Ordering Simple interpolation Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 49 49

B: Inpainting Results – Examples Given data 80% missing pixels Bi-Cubic interpolation DCT and 1 st iteration 3 rd iteration OMP of the recovery proposed alg. Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 50 50

Time To Finish Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 51

Conclusions Processing data is enabled by an appropriate modeling that can expose its inner structure What next? Processing graph data, different patch-embedding, learned dictionaries, lifting scheme, …. Sparsity-based models are highly effective and lead to state-of-the art processing in many disciplines We have shown how classical image processing tasks can benefit from the new construction We have shown how sparsity becomes applicable also for graph structured data These slides can be found in http: //www. cs. technion. ac. il/~elad Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 52 52

Thank you for your time and … Thank you to the organizers of this event: Kenji Fukumizu and Kei Kobayashi Institute of Statistical Mathematics Yoshiyuki Kabashima and Taiji Suzuki Tokyo Institute of Technology Ryota Tomioka Toyota Technological Institute, Chicago for inviting me Questions? Sparse Modeling of Graph-Structured Data … and Images By: Michael Elad 53 53