Sparse Modeling in Image Processing and Deep Learning

Sparse Modeling in Image Processing and Deep Learning Michael Elad Computer Science Department The Technion - Israel Institute of Technology Haifa 32000, Israel New Deep Learning Techniques February 5 -9, 2018 The research leading to these results has been received funding from the European union's Seventh Framework Program (FP/2007 -2013) ERC grant Agreement ERC-SPARSE- 320649

This Lecture Sparseland Sparse Representation Theory Sparsity-Inspired Models CSC Convolutional Sparse Coding ML-CSC Multi -Layered Convolutional Sparse Coding Deep-Learning Another underlying idea that will accompany us Generative modeling of data sources enables o A systematic algorithm development, & o A theoretical analysis of their performance Michael Elad The Computer-Science Department The Technion 2

Multi-Layered Convolutional Sparse Modeling Michael Elad The Computer-Science Department The Technion 3

Our Data is Structured Stock Market Text Documents Matrix Data Biological Signals Social Networks Still Images Videos Seismic Data Radar Imaging o We are surrounded by various diverse sources of massive information o Each of these sources have an internal structure, which can be exploited o This structure, when identified, is the Voice Signals engine behind our ability to process this data Traffic info 3 D Objects Medical Imaging Michael Elad The Computer-Science Department The Technion 4

Models o A model: a mathematical description of the underlying signal of interest, describing our beliefs regarding its structure o The following is a partial list of commonly used models for images o Good models should be simple while matching the signals Simplicity Reliability o Models are almost always imperfect Michael Elad The Computer-Science Department The Technion Principal-Component-Analysis Gaussian-Mixture Markov Random Field Laplacian Smoothness DCT concentration Wavelet Sparsity Piece-Wise-Smoothness C 2 -smoothness Besov-Spaces Total-Variation Beltrami-Flow 5

What This Talk is all About? Data Models and Their Use o Almost any task in data processing requires a model – true for denoising, deblurring, super-resolution, inpainting, compression, anomaly-detection, sampling, recognition, separation, and more o Sparse and Redundant Representations offer a new and highly effective model – we call it Sparseland o We shall describe this and descendant versions of it that lead all the way to … deep-learning Michael Elad The Computer-Science Department The Technion 6

Multi-Layered Convolutional Sparse Modeling Michael Elad The Computer-Science Department The Technion 7

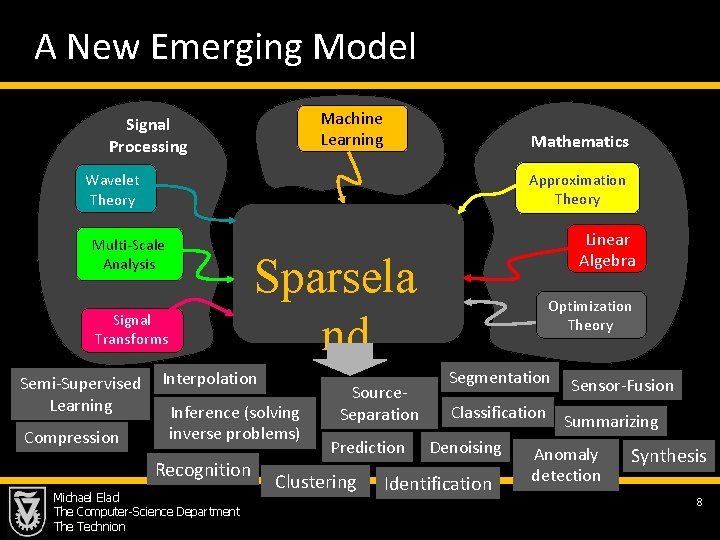
A New Emerging Model Machine Learning Signal Processing Mathematics Approximation Theory Wavelet Theory Multi-Scale Analysis Sparsela nd Signal Transforms Semi-Supervised Learning Compression Linear Algebra Interpolation Inference (solving inverse problems) Recognition Michael Elad The Computer-Science Department The Technion Source. Separation Prediction Clustering Optimization Theory Segmentation Sensor-Fusion Classification Summarizing Denoising Anomaly Identification detection Synthesis 8

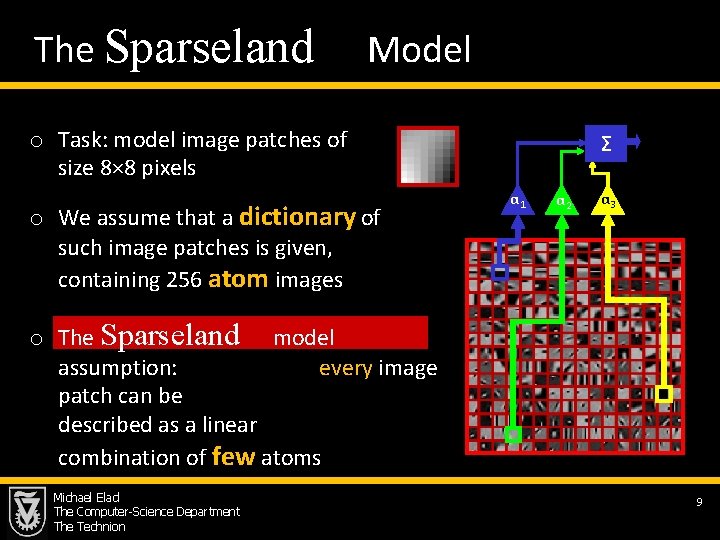
The Sparseland Model o Task: model image patches of size 8× 8 pixels o We assume that a dictionary of such image patches is given, containing 256 atom images Σ α 1 α 2 α 3 o The Sparseland model assumption: every image patch can be described as a linear combination of few atoms Michael Elad The Computer-Science Department The Technion 9

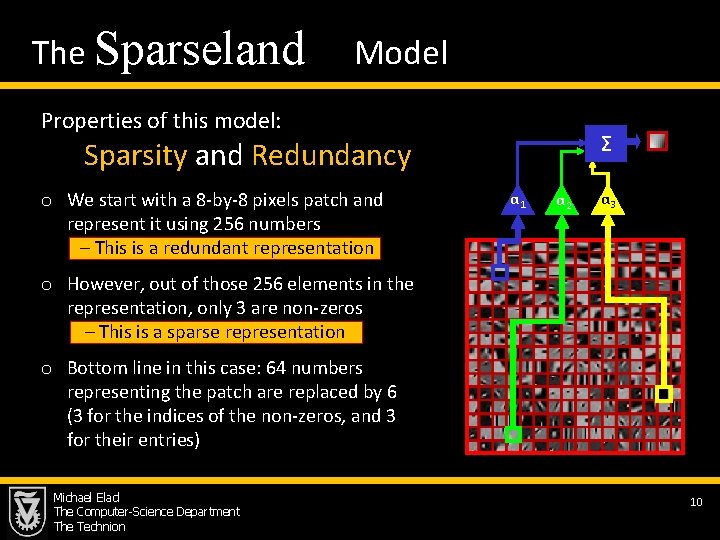
The Sparseland Model Properties of this model: Σ Sparsity and Redundancy o We start with a 8 -by-8 pixels patch and represent it using 256 numbers – This is a redundant representation α 1 α 2 α 3 o However, out of those 256 elements in the representation, only 3 are non-zeros – This is a sparse representation o Bottom line in this case: 64 numbers representing the patch are replaced by 6 (3 for the indices of the non-zeros, and 3 for their entries) Michael Elad The Computer-Science Department The Technion 10

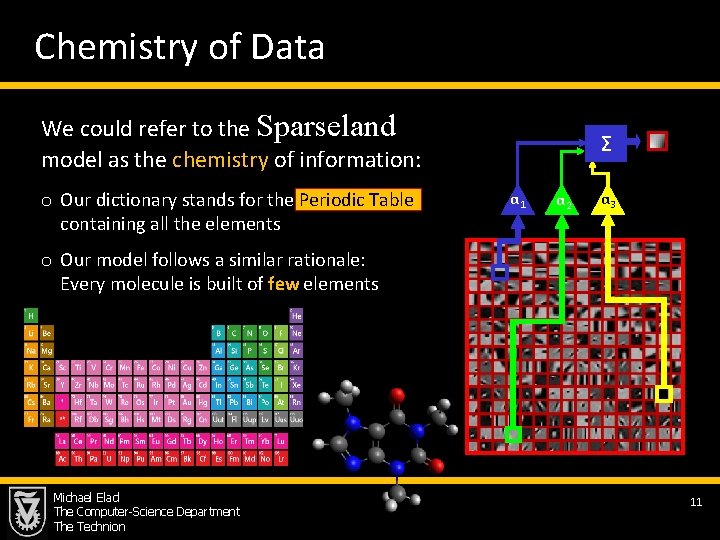
Chemistry of Data We could refer to the Sparseland model as the chemistry of information: o Our dictionary stands for the Periodic Table containing all the elements Σ α 1 α 2 α 3 o Our model follows a similar rationale: Every molecule is built of few elements Michael Elad The Computer-Science Department The Technion 11

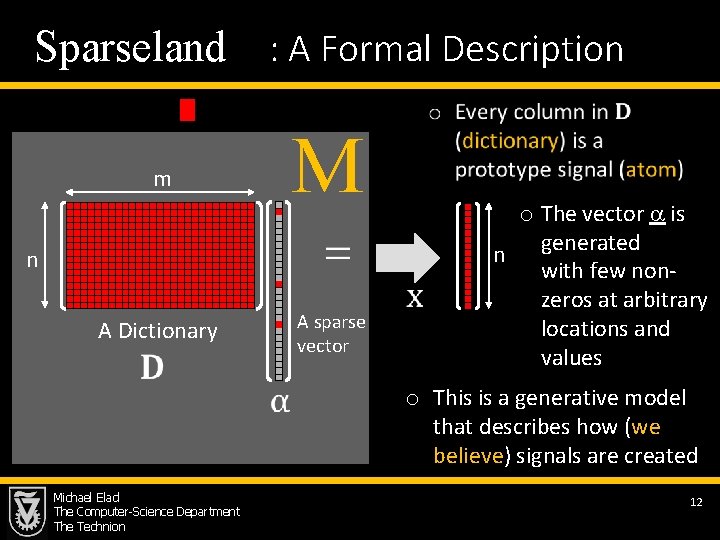
Sparseland : A Formal Description M m n A sparse vector A Dictionary Michael Elad The Computer-Science Department The Technion o The vector is generated n with few nonzeros at arbitrary locations and values o This is a generative model that describes how (we believe) signals are created 12

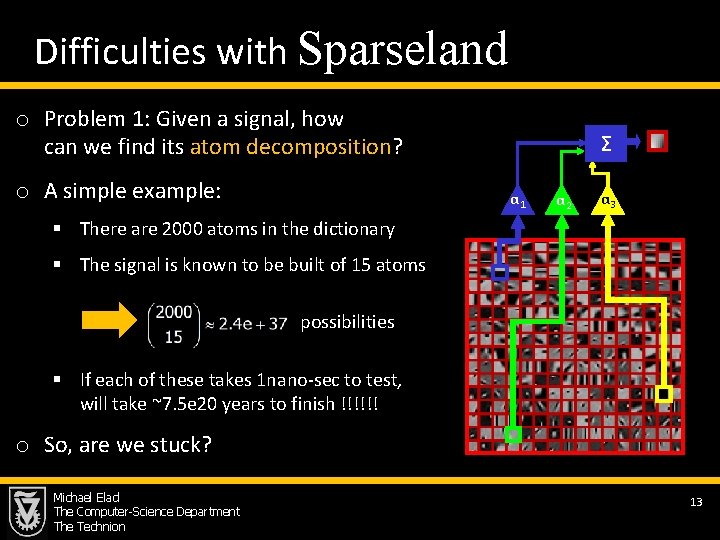
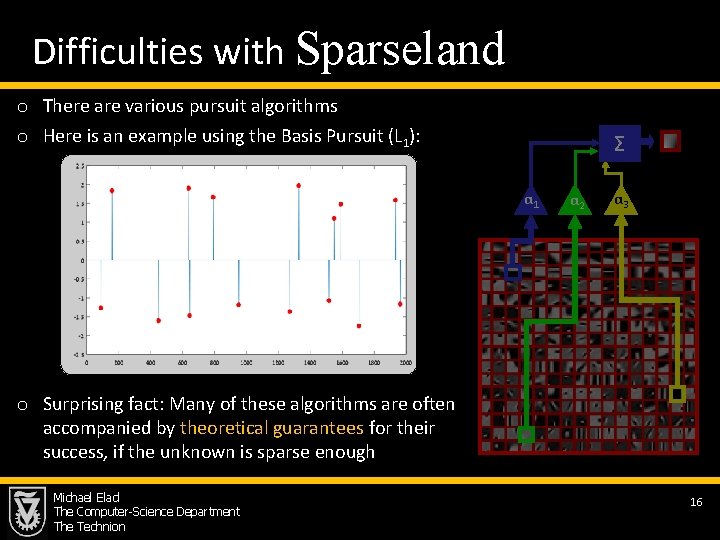
Difficulties with Sparseland o Problem 1: Given a signal, how can we find its atom decomposition? o A simple example: Σ α 1 α 2 α 3 § There are 2000 atoms in the dictionary § The signal is known to be built of 15 atoms possibilities § If each of these takes 1 nano-sec to test, will take ~7. 5 e 20 years to finish !!!!!! this o So, are we stuck? Michael Elad The Computer-Science Department The Technion 13

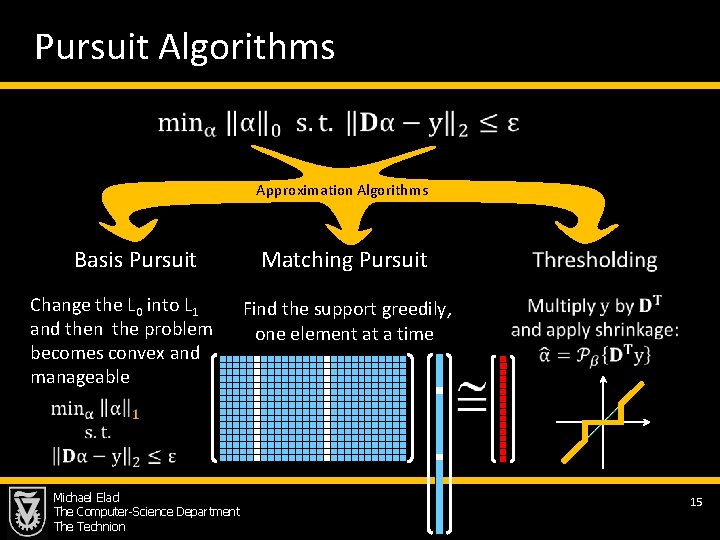
Atom Decomposition Made Formal n m Approximation Algorithms § L 0 – counting number of non-zeros in the vector Relaxation methods Greedy methods Basis-Pursuit Thresholding/OMP Michael Elad The Computer-Science Department The Technion § This is a projection onto the Sparseland model § These problems are known to be NP-Hard problem 14

Pursuit Algorithms Approximation Algorithms Basis Pursuit Change the L 0 into L 1 and then the problem becomes convex and manageable Matching Pursuit Find the support greedily, one element at a time Michael Elad The Computer-Science Department The Technion 15

Difficulties with Sparseland o There are various pursuit algorithms o Here is an example using the Basis Pursuit (L 1): Σ α 1 α 2 α 3 o Surprising fact: Many of these algorithms are often accompanied by theoretical guarantees for their success, if the unknown is sparse enough Michael Elad The Computer-Science Department The Technion 16

The Mutual Coherence o Compute = Assume normalized columns Michael Elad The Computer-Science Department The Technion 17

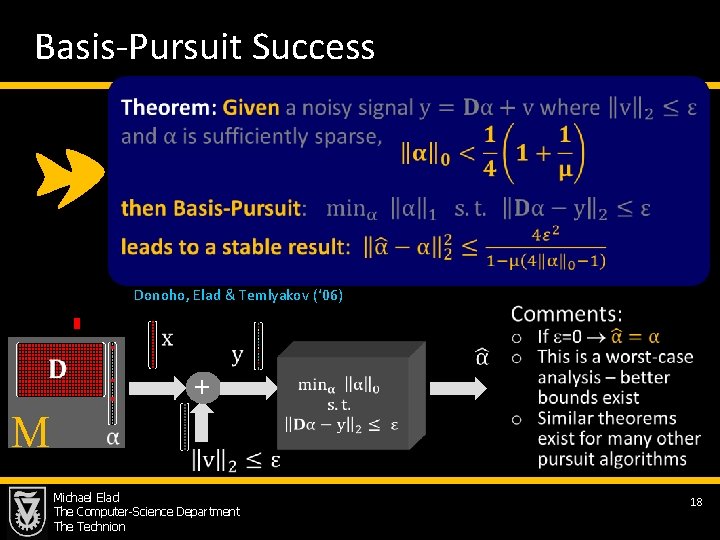
Basis-Pursuit Success Donoho, Elad & Temlyakov (‘ 06) M + Michael Elad The Computer-Science Department The Technion 18

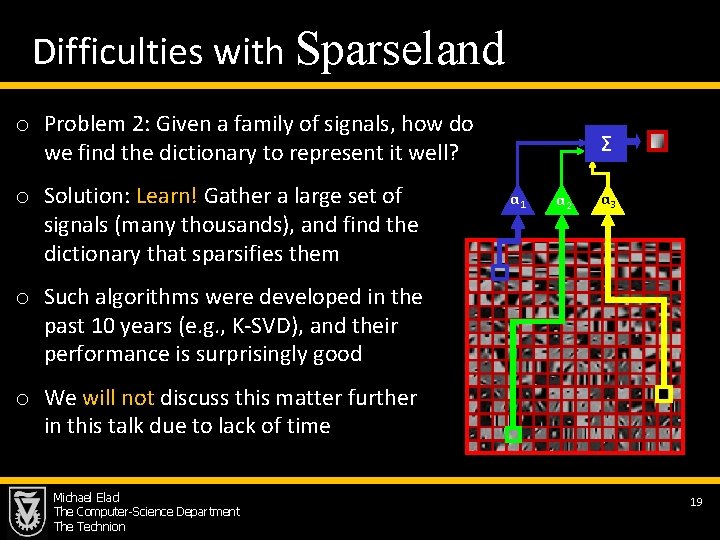
Difficulties with Sparseland o Problem 2: Given a family of signals, how do we find the dictionary to represent it well? o Solution: Learn! Gather a large set of signals (many thousands), and find the dictionary that sparsifies them Σ α 1 α 2 α 3 o Such algorithms were developed in the past 10 years (e. g. , K-SVD), and their performance is surprisingly good o We will not discuss this matter further in this talk due to lack of time Michael Elad The Computer-Science Department The Technion 19

Difficulties with Sparseland o Problem 3: Why is this model suitable to describe various sources? e. g. , Is it good for images? Audio? Stocks? … o General answer: Yes, this model is extremely effective in representing various sources Σ α 1 α 2 α 3 § Theoretical answer: Clear connection to other models § Empirical answer: In a large variety of signal and image processing (and later machine learning), this model has been shown to lead to state-of-the-art results Michael Elad The Computer-Science Department The Technion 20

Difficulties with Sparseland o Problem 1: Given an image patch, how can we find its atom decomposition ? o o D E Problem 2: Given a family of signals, R E Wdictionary Sthe D how do we A find to N N A L Y L L represent A it well? E Y L V I E T V I I S T O C Problem model flexible P 3: Is this U R T various sources? S enough to describe N O C E. g. , Is it good for images? audio? … Michael Elad The Computer-Science Department The Technion ? Σ α 1 α 2 α 3 21

A New Massive Open Online Course Michael Elad The Computer-Science Department The Technion 22

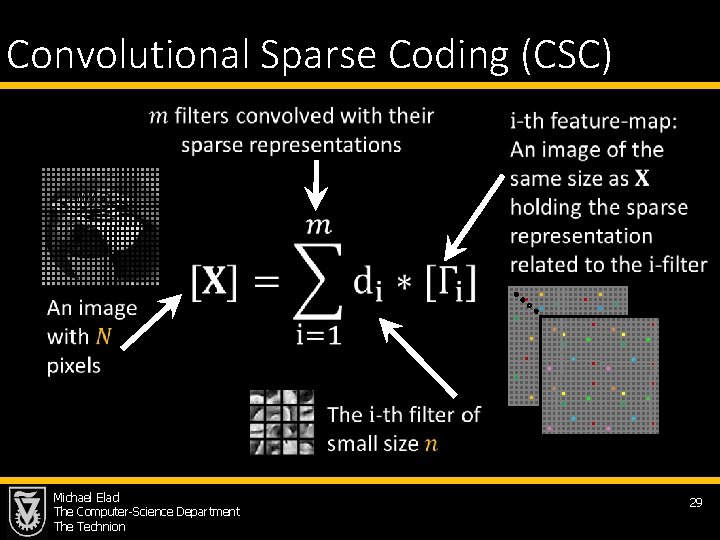
Sparseland for Image Processing o When handling images, Sparseland is typically deployed on small overlapping patches due to the desire to train the model to fit the data better o The model assumption is: each patch in the image is believed to have a sparse representation w. r. t. a common local dictionary o What is the corresponding global model? This brings us to … the Convolutional Sparse Coding (CSC) Michael Elad The Computer-Science Department The Technion 23

Multi-Layered Convolutional Sparse Modeling Joint work with Yaniv Romano Michael Elad The Computer-Science Department The Technion Vardan Papyan Jeremias Sulam 24

Convolutional Sparse Coding (CSC) Michael Elad The Computer-Science Department The Technion 29

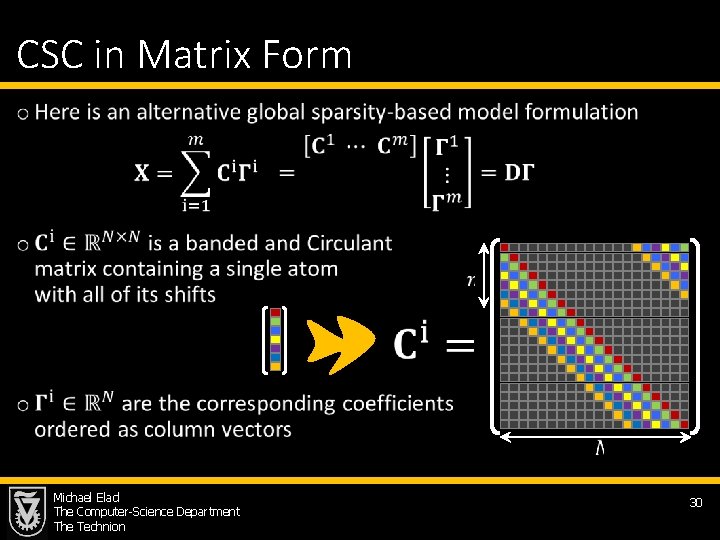
CSC in Matrix Form • Michael Elad The Computer-Science Department The Technion 30

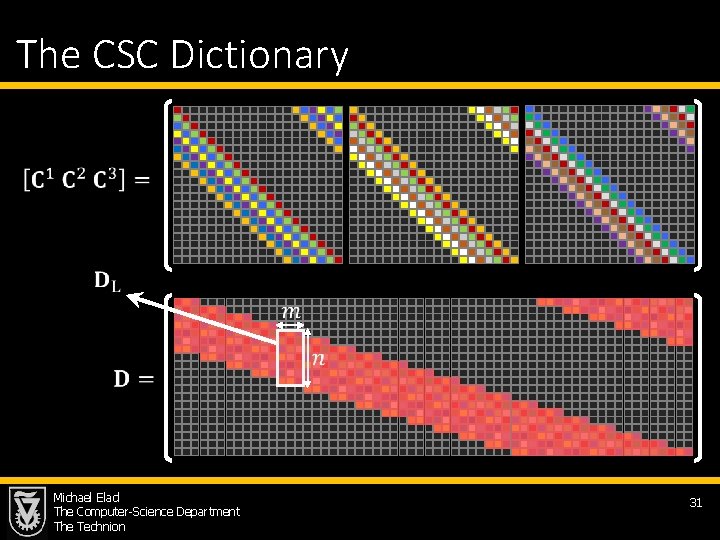
The CSC Dictionary Michael Elad The Computer-Science Department The Technion 31

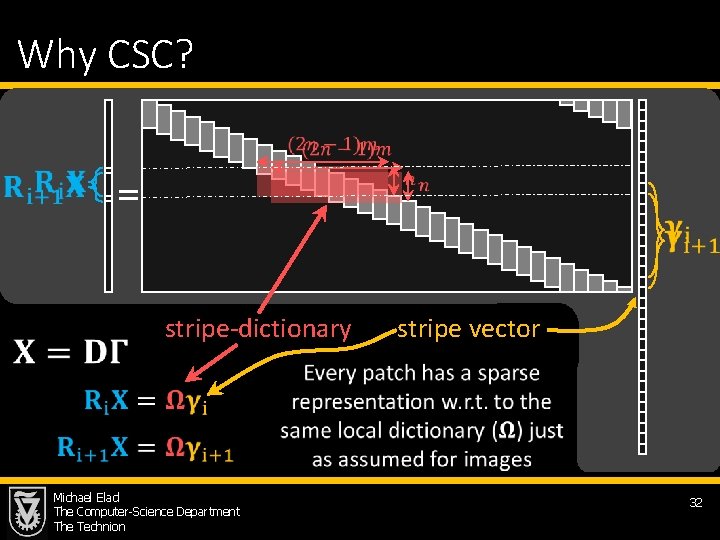
Why CSC? = stripe-dictionary stripe vector Michael Elad The Computer-Science Department The Technion 32

Classical Sparse Theory for CSC ? • ory e h T d n a l e s r ns a o p i t S a c n i s a l s p ex d o The cla o g e vid o r p l t e o d n o m C does S for the C Michael Elad The Computer-Science Department The Technion 33

Moving to Local Sparsity: Stripes The main question we aim to address is this: Can we generalize the vast theory of Sparseland to this new notion of local sparsity? For example, could we provide guarantees for success for pursuit algorithms? Michael Elad The Computer-Science Department The Technion 34

Success of the Basis Pursuit Local noise (per patch) Papyan, Sulam & Elad (‘ 17) Michael Elad The Computer-Science Department The Technion 36

Multi-Layered Convolutional Sparse Modeling Michael Elad The Computer-Science Department The Technion 40

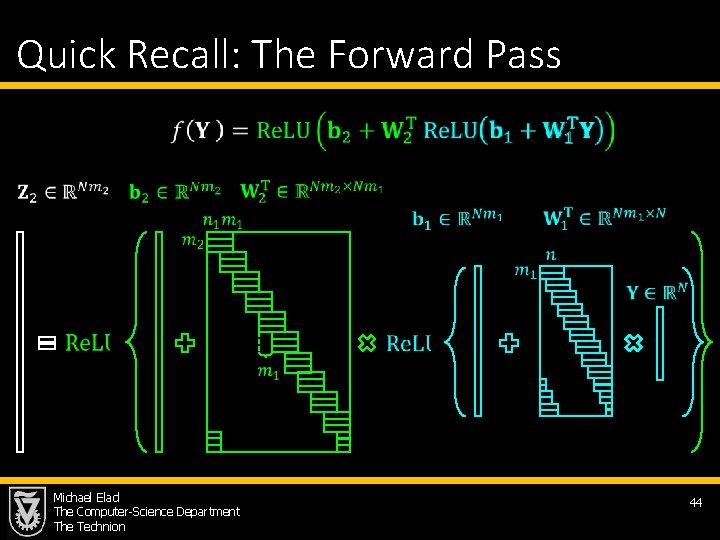
Quick Recall: The Forward Pass Michael Elad The Computer-Science Department The Technion 44

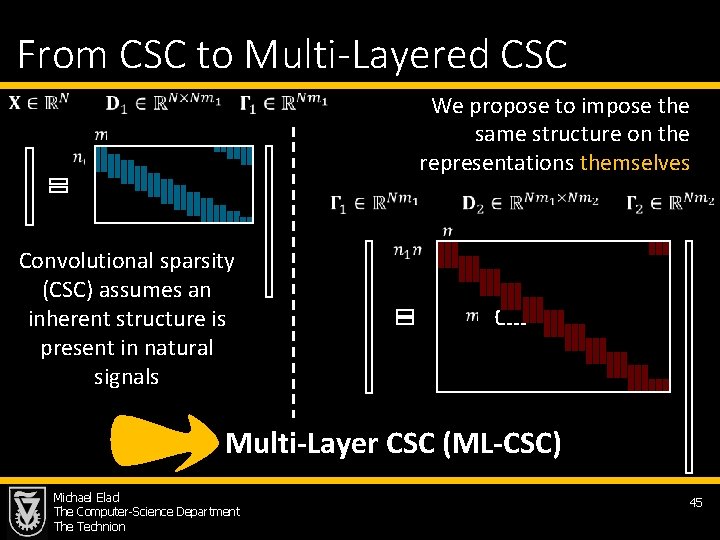
From CSC to Multi-Layered CSC We propose to impose the same structure on the representations themselves Convolutional sparsity (CSC) assumes an inherent structure is present in natural signals Multi-Layer CSC (ML-CSC) Michael Elad The Computer-Science Department The Technion 45

Intuition: From Atoms to Molecules Michael Elad The Computer-Science Department The Technion 46

A Small Taste: Model Training (MNIST) MNIST Dictionary: • D 1: 32 filters of size 7× 7, with stride of 2 (dense) • D 2: 128 filters of size 5× 5× 32 with stride of 1 - 99. 09 % sparse • D 3: 1024 filters of size 7× 7× 128 – 99. 89 % sparse Michael Elad The Computer-Science Department The Technion 47

A Small Taste: Model Training (Ci. FAR) CIFAR Dictionary: • D 1: 64 filters of size 5 x 5 x 3, stride of 2 dense • D 2: 256 filters of size 5 x 5 x 64, stride of 2 82. 99 % sparse • D 3: 1024 filters of size 5 x 5 x 256 90. 66 % sparse Michael Elad The Computer-Science Department The Technion 47

ML-CSC: Pursuit Michael Elad The Computer-Science Department The Technion 48

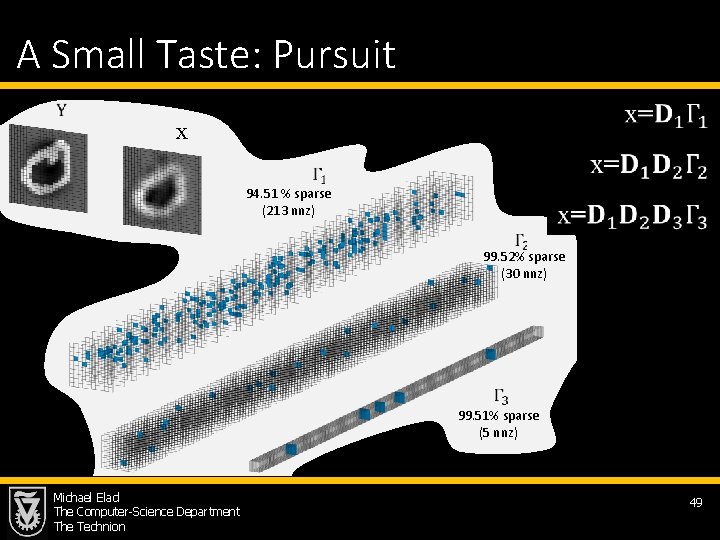
A Small Taste: Pursuit x 94. 51 % sparse (213 nnz) 99. 52% sparse (30 nnz) 99. 51% sparse (5 nnz) Michael Elad The Computer-Science Department The Technion 49

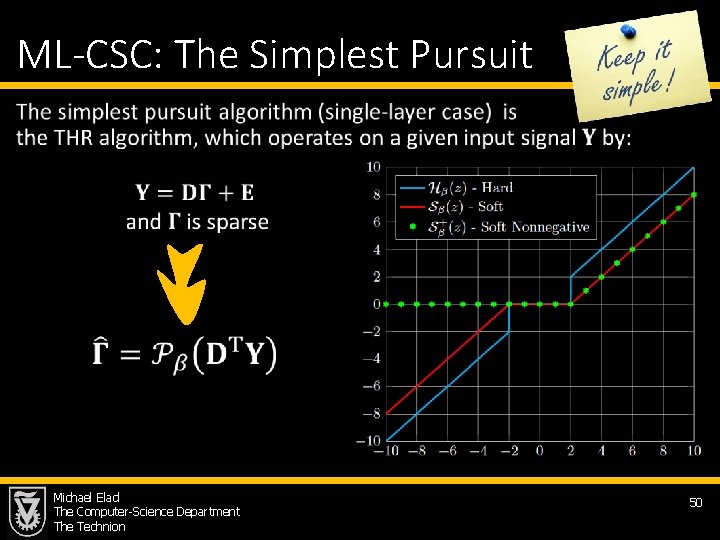
ML-CSC: The Simplest Pursuit • Michael Elad The Computer-Science Department The Technion 50

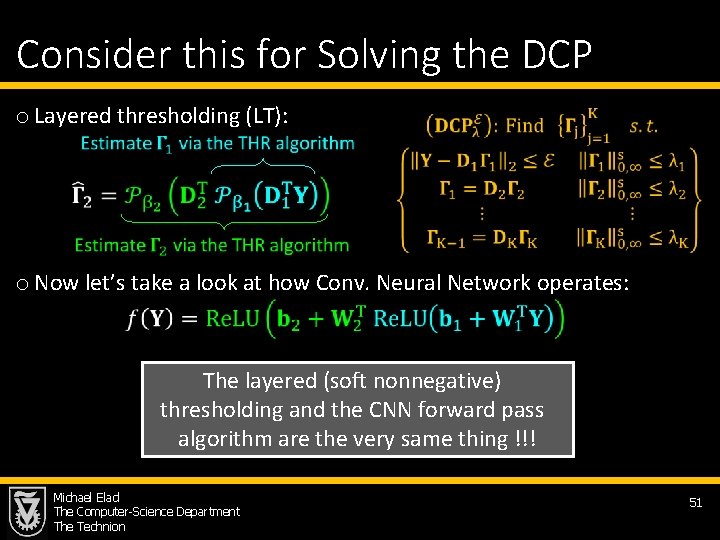
Consider this for Solving the DCP o Layered thresholding (LT): o Now let’s take a look at how Conv. Neural Network operates: The layered (soft nonnegative) thresholding and the CNN forward pass algorithm are the very same thing !!! Michael Elad The Computer-Science Department The Technion 51

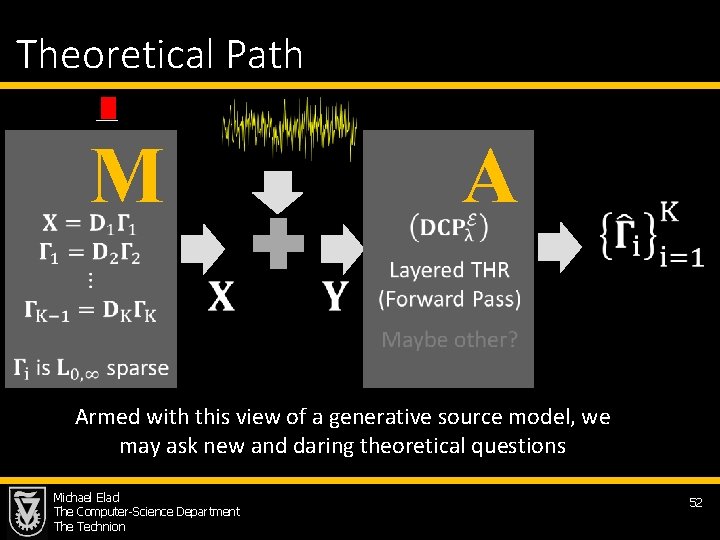
Theoretical Path M A Armed with this view of a generative source model, we may ask new and daring theoretical questions Michael Elad The Computer-Science Department The Technion 52

Success of the Layered-THR Papyan, Romano & Elad (‘ 17) The stability of the forward pass is guaranteed if the underlying representations are locally sparse and the noise is locally bounded Michael Elad The Computer-Science Department The Technion Problems: 1. Contrast 2. Error growth 3. Error even if no noise 54

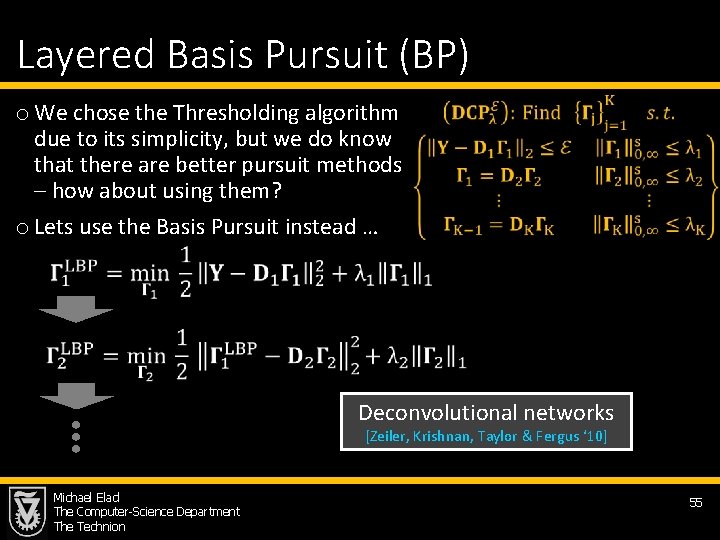
Layered Basis Pursuit (BP) o We chose the Thresholding algorithm due to its simplicity, but we do know that there are better pursuit methods – how about using them? o Lets use the Basis Pursuit instead … Deconvolutional networks [Zeiler, Krishnan, Taylor & Fergus ‘ 10] Michael Elad The Computer-Science Department The Technion 55

Success of the Layered BP Papyan, Romano & Elad (‘ 17) Michael Elad The Computer-Science Department The Technion Problems: 1. Contrast 2. Error growth 3. Error even if no noise 56

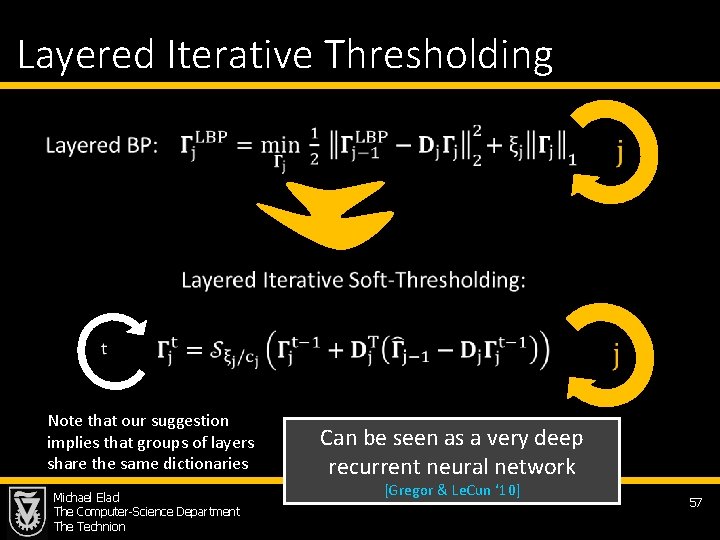
Layered Iterative Thresholding Note that our suggestion implies that groups of layers share the same dictionaries Michael Elad The Computer-Science Department The Technion Can be seen as a very deep recurrent neural network [Gregor & Le. Cun ‘ 10] 57

What About Learning? Sparseland Sparse Representation Theory CSC Convolutional Sparse Coding ML-CSC Multi -Layered Convolutional Sparse Coding o All these models rely on proper Dictionary Learning Algorithms to fulfil their mission: § Sparseland: We have unsupervised and supervised such algorithms, and a beginning of theory to explain how these work § CSC: We have few and only unsupervised methods, and even these are not fully stable/clear § ML-CSC: One algorithm has been proposed (unsupervised) – see Arxi. V Michael Elad The Computer-Science Department The Technion 52

Where are the Labels? Answer 1: M o We do not need labels because everything we show refer to the unsupervised case, in which we operate on signals, not necessarily in the context of recognition We presented the ML-CSC as a machine that produces signals X Michael Elad The Computer-Science Department The Technion 52

Time to Conclude Michael Elad The Computer-Science Department The Technion 58

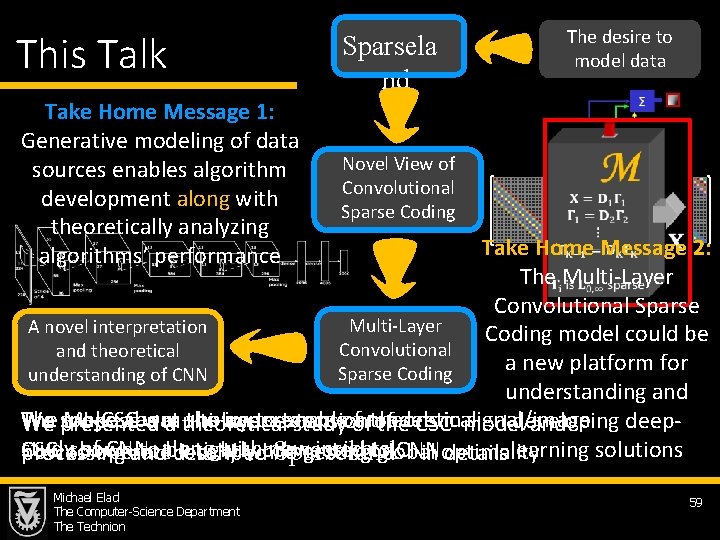
This Talk Take Home Message 1: Generative modeling of data sources enables algorithm development along with theoretically analyzing algorithms’ performance Sparsela nd The desire to model data Novel View of Convolutional Sparse Coding Take Home Message 2: The Multi-Layer Convolutional Sparse Multi-Layer A novel interpretation Coding model could be Convolutional and theoretical a new platform for Sparse Coding understanding of CNN understanding and We spoke The ML-CSC about was the shown importance toextension enable a models theoretical signal/image developing deeppropose a multi-layer of presented a theoretical studyofof the CSCin model and study ofoperate CNN, with new insights CSC, shown to along be tightly connected to CNN how to locally while getting global processing and described Sparseland in optimality details learning solutions Michael Elad The Computer-Science Department The Technion 59

Questions? More on these (including these slides and the relevant papers) can be found in http: //www. cs. technion. ac. il/~elad Michael Elad The Computer-Science Department The Technion