Sparse Matrices and Combinatorial Algorithms in StarP Status

Sparse Matrices and Combinatorial Algorithms in Star-P Status and Plans April 8, 2005

Matlab’s sparse matrix design principles l All operations should give the same results for sparse and full matrices (almost all) l Sparse matrices are never created automatically, but once created they propagate l Performance is important -- but usability, simplicity, completeness, and robustness are more important l Storage for a sparse matrix should be O(nonzeros) l Time for a sparse operation should be O(flops) (as nearly as possible)

Matlab’s sparse matrix design principles l All operations should give the same results for sparse and full matrices (almost all) l Sparse matrices are never created automatically, but once created they propagate l Performance is important -- but usability, simplicity, completeness, and robustness are more important l Storage for a sparse matrix should be O(nonzeros) l Time for a sparse operation should be O(flops) (as nearly as possible) Star-P dsparse matrices: same principles, some different tradeoffs

Sparse matrix operations l dsparse layout, same semantics as ddense l For now, only row distribution l Matrix operators: +, -, max, etc. l Matrix indexing and concatenation A (1: 3, [4 5 2]) = [ B(: , 7) C ] ; l A b by direct methods
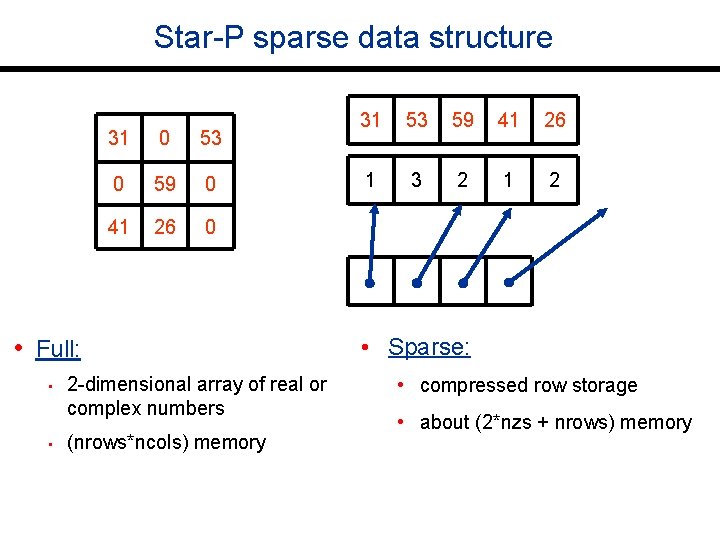
Star-P sparse data structure 31 0 53 0 59 0 41 26 0 • Full: • • 2 -dimensional array of real or complex numbers (nrows*ncols) memory 31 53 59 41 26 1 3 2 1 2 • Sparse: • compressed row storage • about (2*nzs + nrows) memory
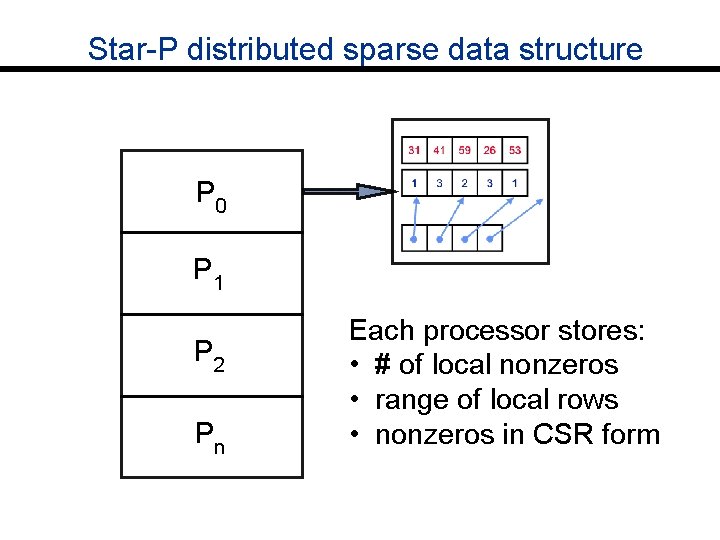
Star-P distributed sparse data structure P 0 P 1 P 2 Pn Each processor stores: • # of local nonzeros • range of local rows • nonzeros in CSR form
![Sorting in Star-P l [V, perm] = sort (V) l Useful primitive for some Sorting in Star-P l [V, perm] = sort (V) l Useful primitive for some](http://slidetodoc.com/presentation_image_h/105cd7fa2d4b8492b9e6d061599441aa/image-7.jpg)
Sorting in Star-P l [V, perm] = sort (V) l Useful primitive for some sparse array algorithms, e. g. the sparse constructor l Star-P uses a parallel sample sort

The sparse( ) constructor l A = sparse (I, J, V, nr, nc) l Input: ddense vectors I, J, V, and dimensions nr, nc l A(I(k), J(k)) = V(k) for each k l Sort triples (i, j, v) by (i, j) l Adjust for desired row distribution l Locally convert to compressed row indices l Sum values with duplicate indices

Sparse matrix times dense vector l y=A*x l The first call to matvec caches a communication schedule for matrix A. Later calls to multiply any vector by A use the cached schedule. l Communication and computation overlap.

Sparse linear systems l x=Ab l Matrix division uses MPI-based direct solvers: 0 Super. LU_dist: nonsymmetric static pivoting 0 MUMPS: nonsymmetric multifrontal 0 PSPASES: Cholesky ppsetoption(’Sparse. Direct. Solver’, ’SUPERLU’) l Iterative solvers implemented in Star-P l Ongoing work on preconditioners
![Sparse eigenvalue solvers l [V, D] = eigs(A); l Implemented via MPI-based PARPACK etc. Sparse eigenvalue solvers l [V, D] = eigs(A); l Implemented via MPI-based PARPACK etc.](http://slidetodoc.com/presentation_image_h/105cd7fa2d4b8492b9e6d061599441aa/image-11.jpg)
Sparse eigenvalue solvers l [V, D] = eigs(A); l Implemented via MPI-based PARPACK etc. [Lehoucq, Maschhoff, Sorensen, Yang] l Work in progress

Combinatorial Scientific Computing l Sparse matrix methods; machine learning; search and information retrieval; adaptive multilevel modeling; geometric meshing; computational biology; . . . l How will combinatorial methods be used by people who don’t understand them in complete detail?

Analogy: Matrix division in Matlab x = A b; l Works for either full or sparse A l Is A square? no => use QR to solve least squares problem l Is A triangular or permuted triangular? yes => sparse triangular solve l Is A symmetric with positive diagonal elements? yes => attempt Cholesky after symmetric minimum degree l Otherwise => use LU on A(: , colamd(A))

Combinatorics in Star-P l A sparse matrix language is a good start on primitives for combinatorial computing. 0 Random-access indexing: A(i, j) 0 Neighbor sequencing: find (A(i, : )) 0 Sparse table construction: sparse (I, J, V) l Other primitives we are building: sorting, searching, pointer-jumping, connectivity and paths, . . .

Matching and depth-first search in Matlab l dmperm: Dulmage-Mendelsohn decomposition l Square, full rank A: l Arbitrary A: 0[p, q, r] = dmperm(A); 0 A(p, q) is block upper triangular with nonzero diagonal 0 also, strongly connected components of a directed graph 0 also, connected components of an undirected graph 0[p, q, r, s] = dmperm(A); 0 maximum-size matching in a bipartite graph 0 minimum-size vertex cover in a bipartite graph 0 decomposition into strong Hall blocks

Connected components (work in progress) l Sequential Matlab uses depth-first search (dmperm), which doesn’t parallelize well l Shiloach-Vishkin algorithm: 0 repeat Link every (super)vertex to a random neighbor u Shrink each tree to a supervertex by pointer jumping 0 until no further change u l Hybrid SV / search method under construction l Other potential graph kernels: 0 Breadth-first search (after Husbands, LBNL) 0 Bipartite matching (after Riedy, UCB) 0 Strongly connected components (after Pinar, LBNL)

SSCA #2 -- Overview SSCA #2: Directed weighted multigraph with no self-loops l l l Randomly sized “cliques” Most intra-clique edges present Random inter-clique edges, gradually 'thinning' with distance Integer and character string edge labels Randomized vertex numbers l l l Scalable data generator Kernel 1 — Graph Construction Kernel 2 — Classify Large Sets (Search) Kernel 3 — Subgraph Extraction Kernel 4 — Graph Clustering / Partitioning MIT Lincoln Laboratory
HPCS Benchmark Spectrum SSCA #2 MIT Lincoln Laboratory

Scalable Data Generator l l l Produce edge tuples containing the start vertex, end vertex, and weight for each directed edge 0 Hierarchical nature, with random-sized cliques connected by edges between some of the cliques 0 Interclique edges are assigned using a random distribution that represents a hierarchical thinning as vertices are further apart 0 Weights are either random integer values or randomly selected character strings 0 Random permutations to avoid induced locality u Vertex numbers — local processor memory locality u Parallel — global memory locality Data sets must be developed in their entirety before graph construction May be parallelized — data tuple vertex naming schemes must be globally consistent Data generator will not be timed Statistics will be saved to be used in later verification stages MIT Lincoln Laboratory

Kernel 1 — Graph Construction l Construct the multigraph in a format usable by all subsequent kernels l No subsequent modifications will be permitted to benefit specific kernels l Graph construction will be timed MIT Lincoln Laboratory

Kernel 2 — Sort on Selected Edge Weights l Sort on edge weights to determine those vertex pairs with 0 The largest integer weights 0 With a desired string weight l The two vertex pair lists will be saved for use in the subsequent kernel 0 Start set SI for integer start sets 0 Start set SC for character start sets l Sorting weights will be timed MIT Lincoln Laboratory

Kernel 3 — Extract Subgraphs l Extract a series of subgraphs formed by following paths of length k from a start set of initial vertices l The set of initial vertices will be determined from the previous kernel l Produce a series of subgraphs consisting of vertices and edges on paths of length k from the vertex pairs start sets SI and SC l A possible computational kernel for graph extraction is Breadth First Search l Extracting graphs will be timed MIT Lincoln Laboratory

Kernel 4 — Partition Graph Using a Clustering Algorithm l Apply a graph clustering algorithm to partition the vertices of the graph into subgraphs no larger than a maximum size so as to minimize the number of edges that need be “cut”, e. g. 0 Kernighan and Lin 0 Sangiovanni-Vincentelli, Chen, and Chua l The output of this kernel will be a description of the clusters and the edges that form the interconnecting “network” l This step should identify the structure in the graph specified in the data generation phase l It is important that the implementation of this kernel does not utilize a priori knowledge of the details in the data generator or the statistics collected in the graph generation process l Identifying the clusters and the interconnecting “network” will be timed MIT Lincoln Laboratory

Concise SSCA#2 l A serial Matlab implementation of SSCA#2 l Coding style is simple and “data parallel” l Our starting point for Star-P implementation l Edge labels are only integers, not strings yet

Data generation l Using Lincoln Labs serial Matlab generator at present l Data-parallel Star-P generator under construction l Generate “edge triples” as distributed dense vectors

Kernel 1: Graph construction l c. SSCA#2 K 1: ~30 lines of executable serial Matlab l Multigraph is a cell array of simple directed graphs l Graphs are dsparse matrices, created by sparse( )

Kernel 2: Search in large sets l c. SSCA#2 K 2: ~12 lines of executable serial Matlab l Uses max( ) and find( ) to locate edges of max weight ng = length(G. edge. Weights); % number of graphs maxwt = 0; for g = 1: ng maxwt = max(maxwt, max(G. edge. Weights{g}))); end intedges = zeros(0, 2); for g = 1: ng [intstart intend] = find(G. edge. Weights{g} == maxwt); intedges = [intedges ; intstart intend]; end;

Kernel 3: Subgraph extraction l c. SSCA#2 K 3: ~25 lines of executable serial Matlab l Returns subgraphs consisting of vertices and edges within specified distance of specified starting vertices l Sparse matrix-vector product for breadth-first search

Kernel 4: Partitioning / clustering l c. SSCA#2 K 4: serial prototype exists, not yet parallel l Different algorithm from Lincoln Labs executable spec, which uses seed-growing breadth-first search l c. SSCA#2 uses spectral methods for clustering, based on eigenvectors (Fiedler vectors) of the graph l One version seeks small balanced edge cuts (graph partitioning); another seeks clusters with low isoperimetric number (clustering)
- Slides: 29