SPARSE DISTANCE METRIC LEARNING IN HIGHDIMENSIONAL SPACE VIA

SPARSE DISTANCE METRIC LEARNING IN HIGH-DIMENSIONAL SPACE VIA L 1 -PERNALIZED LOGDETERMINANT DIVERGENCE Authors: Guo-Jun Qi, Dept. ECE, UIUC Jinhui Tang, Zheng-Jun Zha, Tat-Seng Chua SOC, NUS Hong-Jiang Zhang Microsoft ATC

OUTLINE Motivations Sparse Distance Metric Formulations Optimization Efficient L 1 -Penalized Log-Determinant Solver Consistency by L 1 Experiments Results

OUTLINE Motivations Sparse Distance Metric Formulations Optimization Efficient L 1 -Penalized Log-Determinant Solver Consistency by L 1 Experiments Results

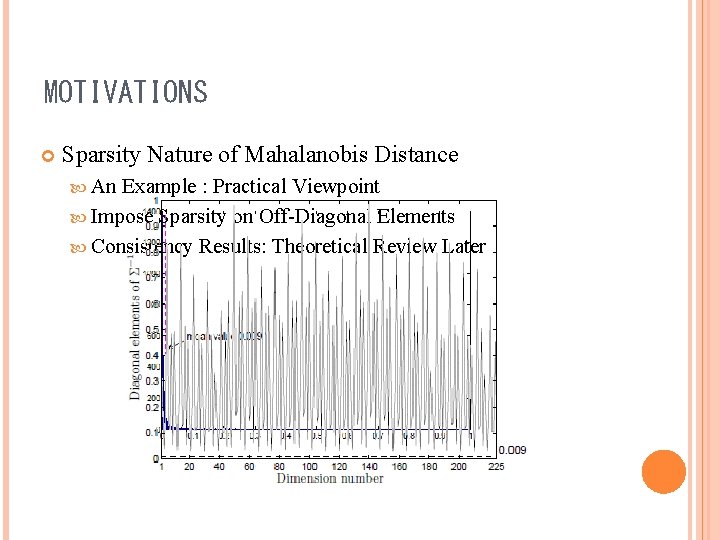
MOTIVATIONS Sparsity Nature of Mahalanobis Distance An Example : Practical Viewpoint Impose Sparsity on Off-Diagonal Elements Consistency Results: Theoretical Review Later

OUTLINE Motivations Sparse Distance Metric Formulations L 1 Optimization Efficient L 1 -Penalized Log-Determinant Solver Consistency Experiments Results

FORMULATION Learn a Mahalanobis Distance Criterion: Given similar pairs S and dissimilar pairs D, the learned d. M has smaller distance on S and larger distance on D

FORMULATION (CON’T) Loss function

FORMULATION (CON’T) ØM 0 is the prior Mahalanobis matrix n Euclidean prior: M 0 is the identity matrix n. Covariance prior: M 0 is the covariance matrix, reflecting the sample distribution

L 1 OPTIMIZATION A Natural Solution: Convert into SDP problem Let Problem: Too expensive computational cost!

OUTLINE Motivations Sparse Distance Metric Formulations Optimization Efficient L 1 -Penalized Log-Determinant Solver Consistency by L 1 Experiments Results

EFFICIENT L 1 -PENALIZED LOG-DETERMINANT SOLVER Block coordinate descent algorithm (Friedman et al. , 2007) Let W be an estimation of M-1 and An efficient Iterative procedure

OUTLINE Motivations Sparse Distance Metric Formulations Optimization Efficient L 1 -Penalized Log-Determinant Solver Consistency by L 1 Experiments Results

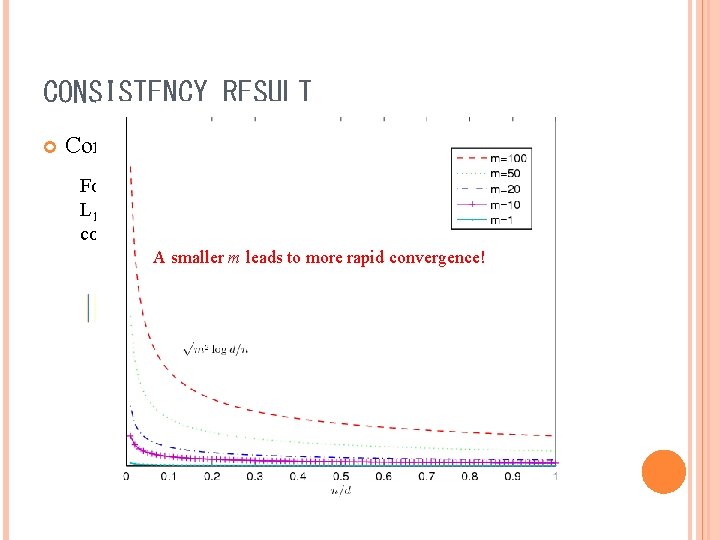
CONSISTENCY RESULT Consistency rate For a target Mahalanobis matrix at most m nonzero per row, L 1 -pernalized log-determinant formulaton leads to the consistency rate A smaller m leads to more rapid convergence!

OUTLINE Motivations Sparse Distance Metric Formulations Optimization Efficient L 1 -Penalized Log-Determinant Solver Consistency by L 1 Experiments Results

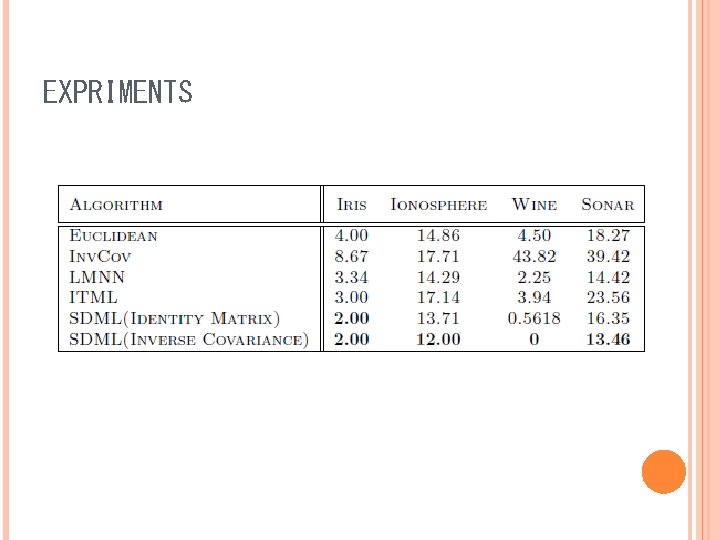
EXPERIMENTS Datasets UCI datasets – IRIS, IONOSPHERE, WINE, SONAR Image datasets – COREL Compared methods EUCLIDEAN INVCOV LMNN ITML

EXPRIMENTS

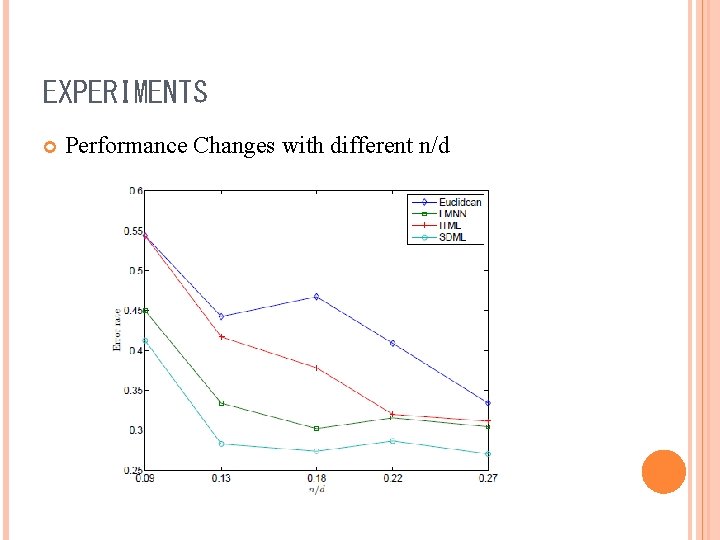
EXPERIMENTS Performance Changes with different n/d

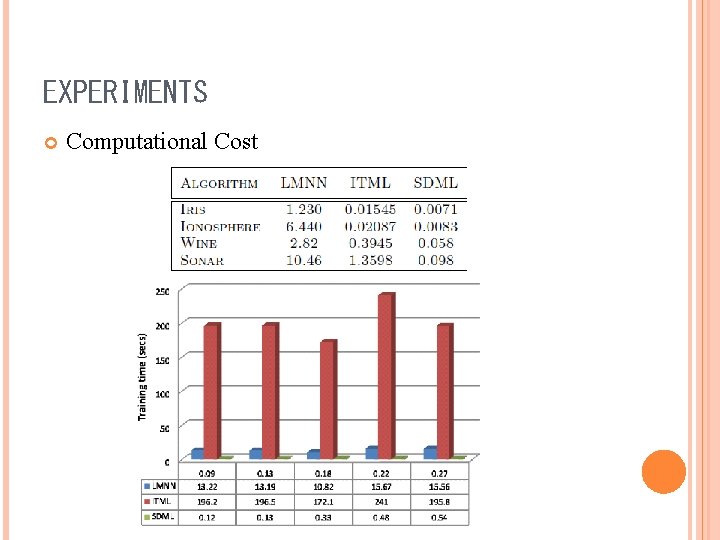
EXPERIMENTS Computational Cost

OUTLINE Motivations Sparse Distance Metric Formulations Optimization Efficient by L 1 -Penalized Log-Determinant Solver Consistency Experiments Conclusion Results

CONCLUSIONS L 1 -penalized log-determinant formulation to learn Mahalanobis distance A consistency rate which prefers a sparsity assumption An efficiently L 1 solver

Thanks for Attention ! Q & A