Space Weather Magnetic Field Origins Helioseismology Dynamo Theory

Space Weather Magnetic Field Origins Helioseismology Dynamo Theory 1

Motivation • Solar magnetic fields are the driver of space weather; without the magnetic field there is no space weather. Can someone tell me why that is? • Magnetic fields originate under the solar surface. • There are short and long term changes in the fields. • How can we predict these changes? 2

Outline • Helioseismology – What is it – What are the measurements – What is the mathematics – What do the results look like • Solar Dynamo – Basic concept What is a dynamo? – Current understanding (pun not intended) 3

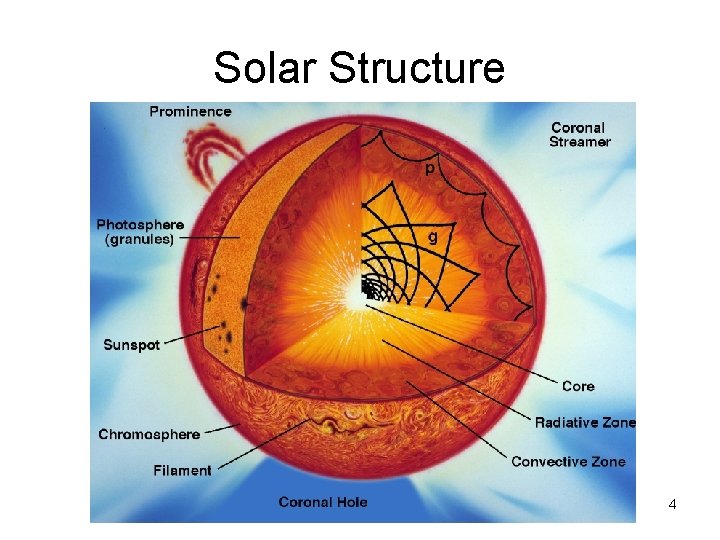
Solar Structure 4

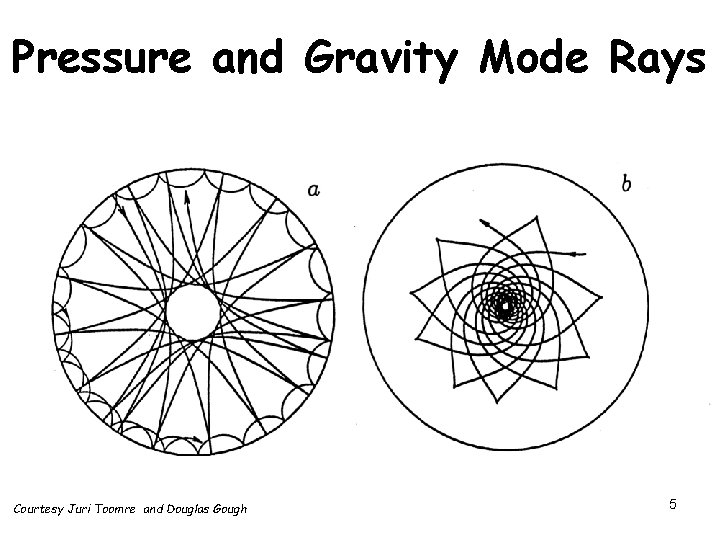
Pressure and Gravity Mode Rays Courtesy Juri Toomre and Douglas Gough 5

Helioseismology • Phenomenon • 5 minute oscillations of the visible surface • Sound waves • resonantly trapped below the surface • excited by convection just below the surface • Methodology • 107 normal modes of varying radial/latitudinal extent • Comparison of frequencies with model calculations • Inverse methods • Local helioseismology and running waves • Results • Physics: GR, neutrinos, Eo. S, opacities, diffusion, • Stellar Structure: temperature, density, abundances, rotation, flows, "turbulence", . . . Implies stellar evolution. • Variability: modes, 3 -D structures • Frontier • Asteroseismology • Gravity Modes 6

The Solar Surface Courtesy of Luc Rouppe van der Voort, Oslo, from the Swedish Solar Telescope, La Palma 7

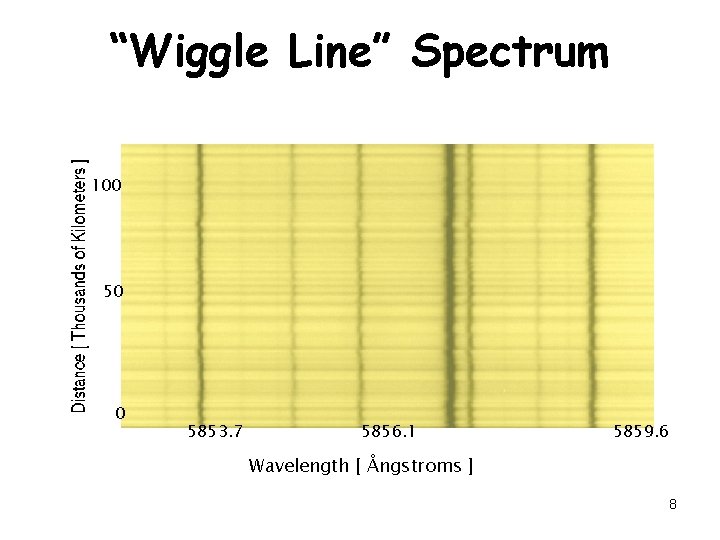
“Wiggle Line” Spectrum 100 50 0 5853. 7 5856. 1 5859. 6 Wavelength [ Ångstroms ] 8

Telescope • Ordinary white light telescope, need not be very large, good enough for 1” resolution • Blocking filter to isolate one desirable spectral line • Tunable interference filter to make measurements in several locations through line to make Doppler line profiles. • CCD detector. • Output is a line profile at each 1” element on the Sun 9

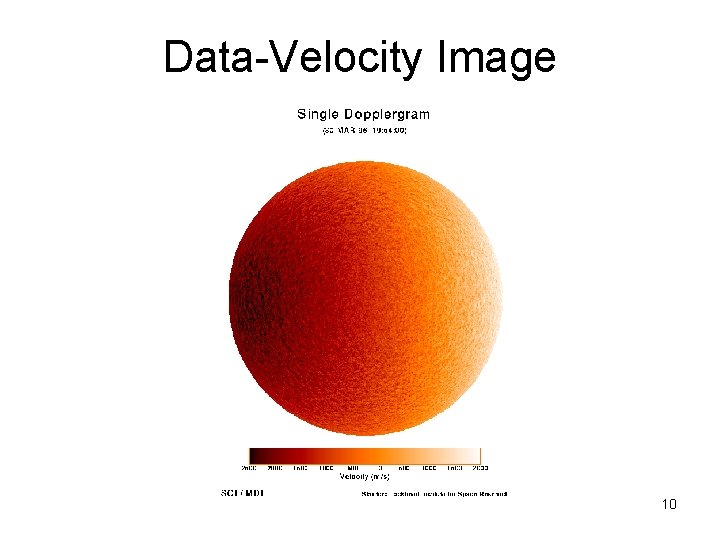
Data-Velocity Image 10

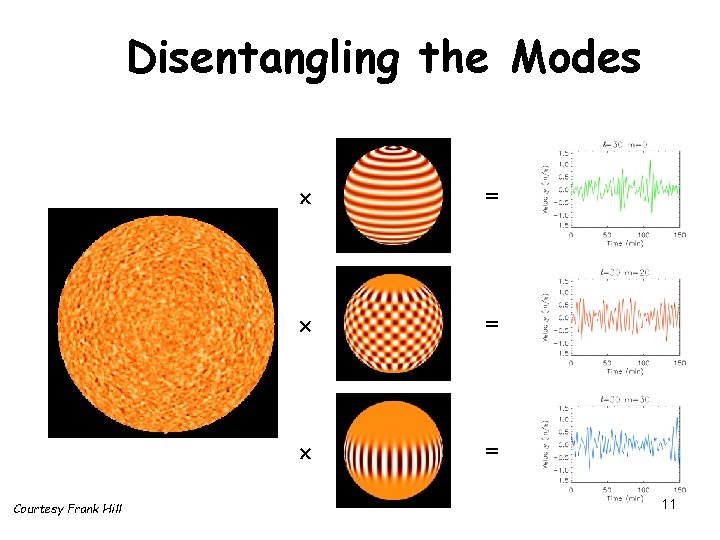
Disentangling the Modes Courtesy Frank Hill = = = 11

Mathematical Form From Annual Reviews of Astronomy and Astrophysics 1984, 22, 593, Deubner and Gough 12

Equation of Motion 13

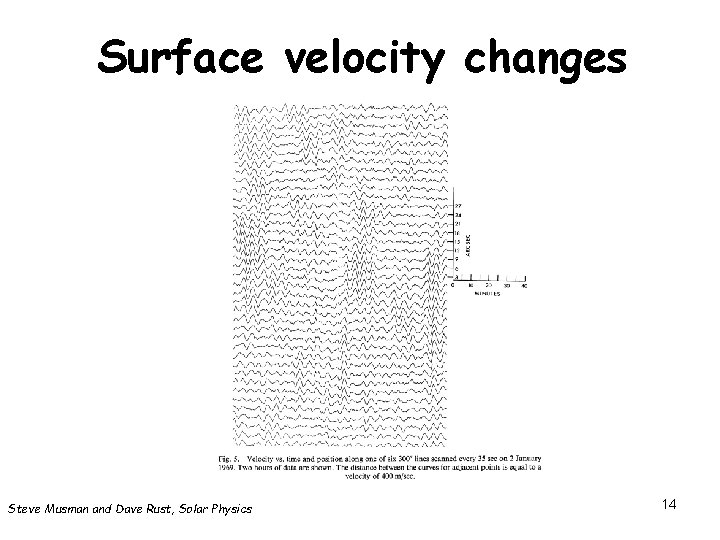
Surface velocity changes Steve Musman and Dave Rust, Solar Physics 14

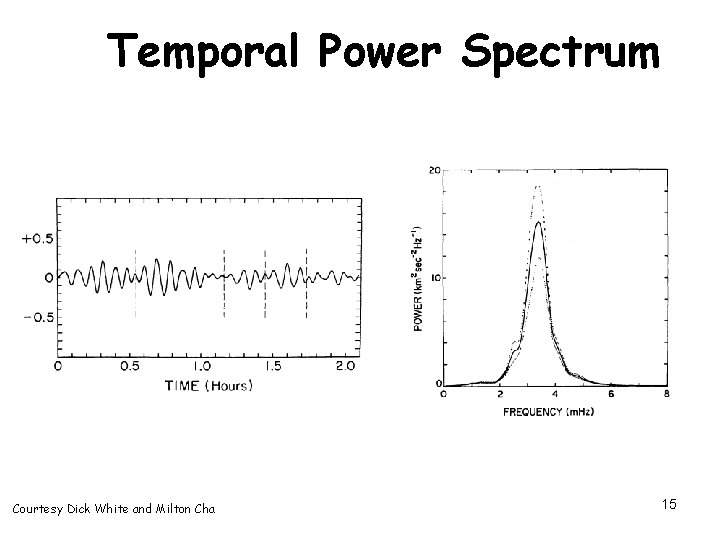
Temporal Power Spectrum Courtesy Dick White and Milton Cha 15

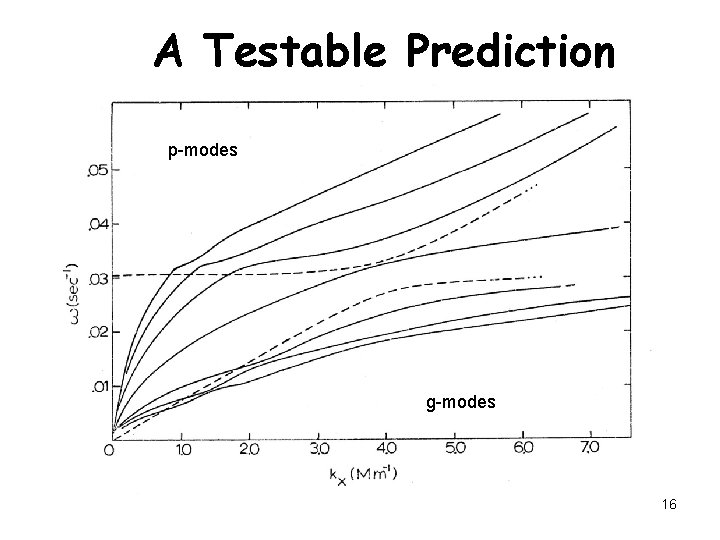
A Testable Prediction p-modes g-modes 16

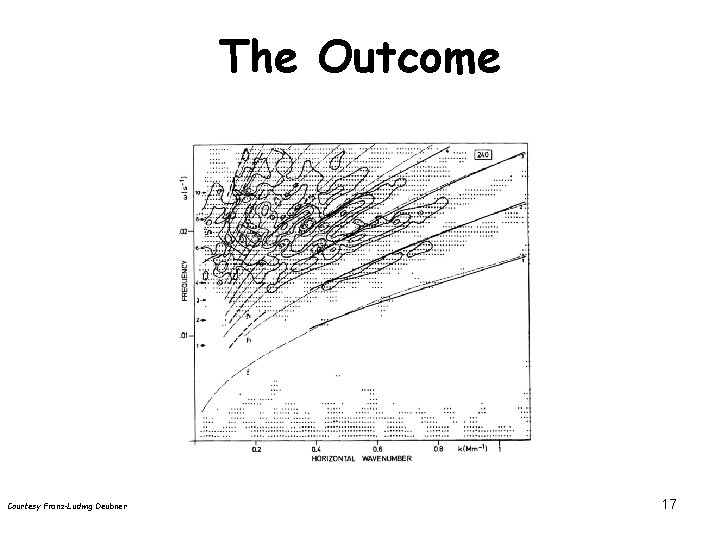
The Outcome Courtesy Franz-Ludwig Deubner 17

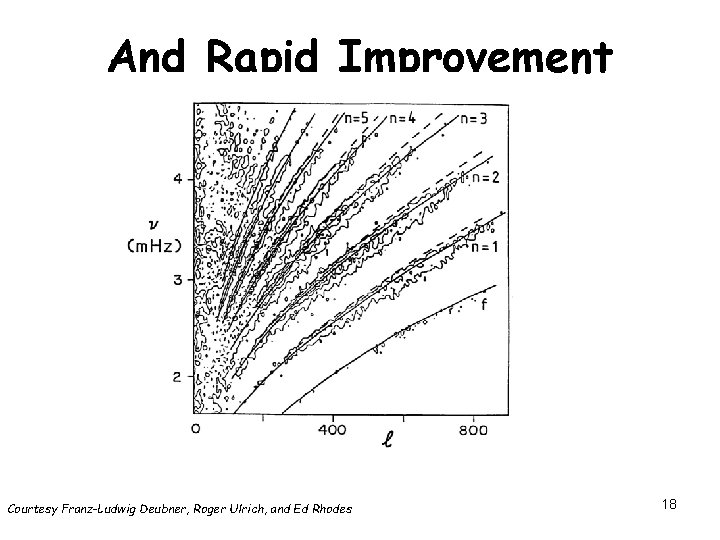
And Rapid Improvement Courtesy Franz-Ludwig Deubner, Roger Ulrich, and Ed Rhodes 18

Caricature of the “Scientific Method” • Serendipitous Discovery • Many Different Descriptions • Testable Prediction of Unobserved Phenomenon • Confirmation • Use Remaining Small Deviations as Tool 19

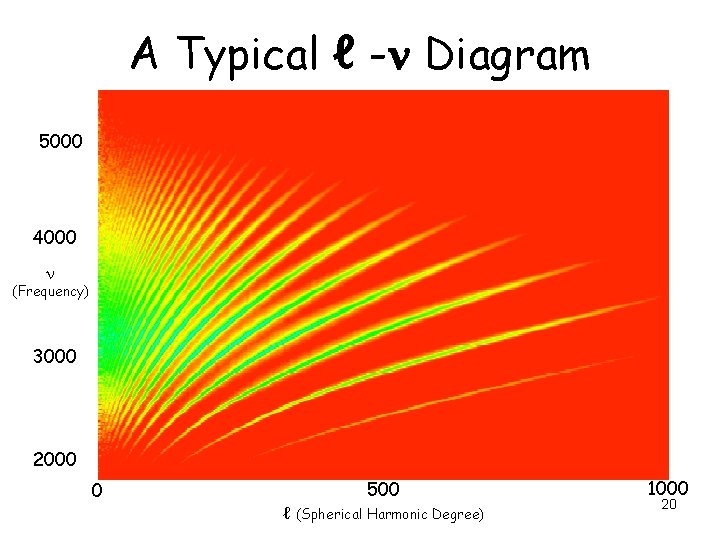
A Typical ℓ - Diagram 5000 4000 (Frequency) 3000 2000 500 ℓ (Spherical Harmonic Degree) 1000 20 0

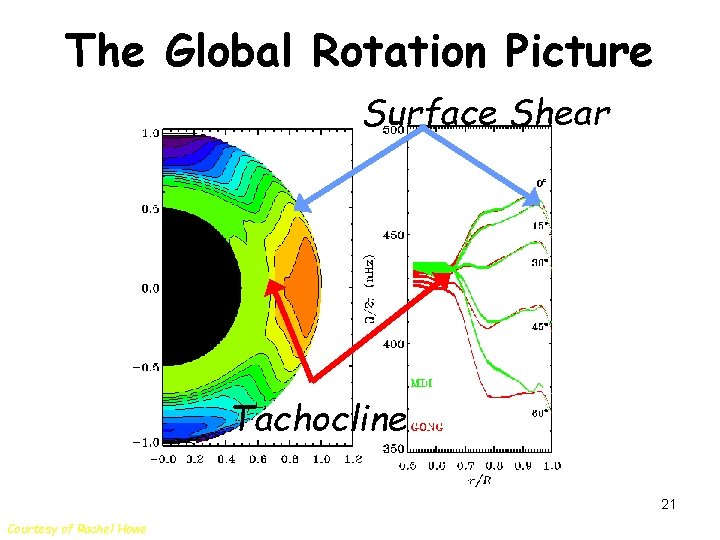
The Global Rotation Picture Surface Shear Tachocline 21 Courtesy of Rachel Howe

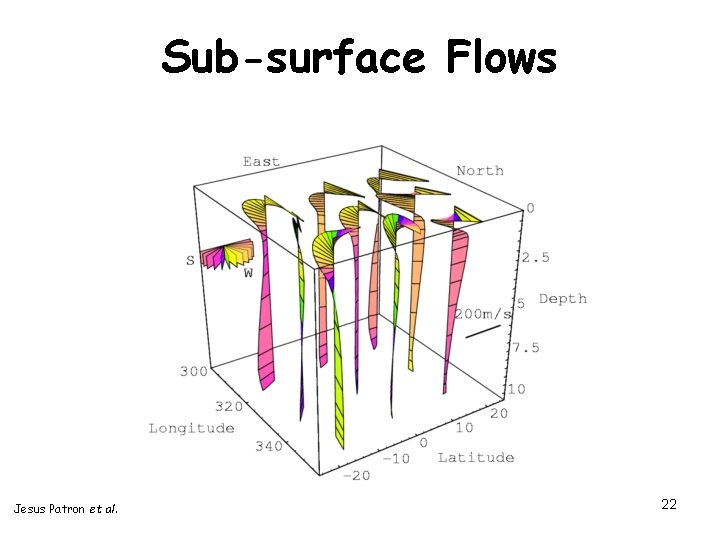
Sub-surface Flows Jesus Patron et al. 22

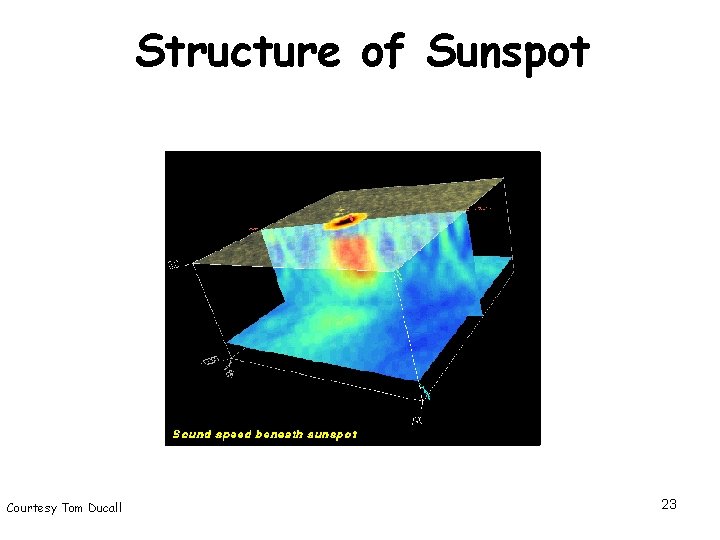
Structure of Sunspot Courtesy Tom Ducall 23

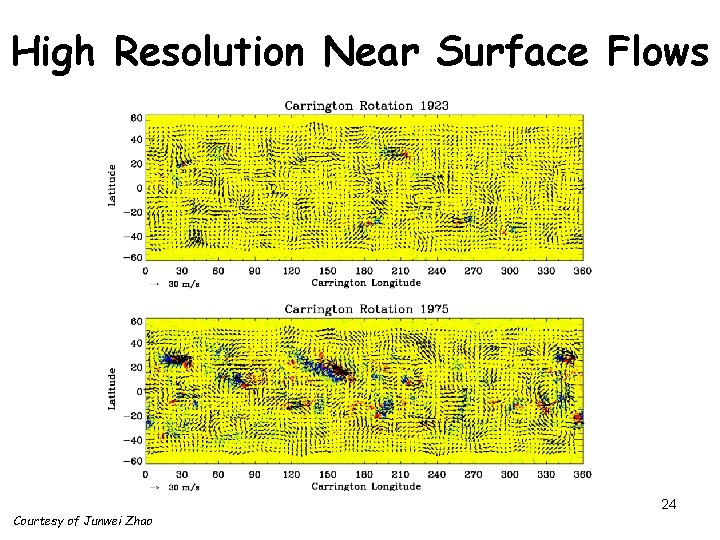
High Resolution Near Surface Flows Courtesy of Junwei Zhao 24

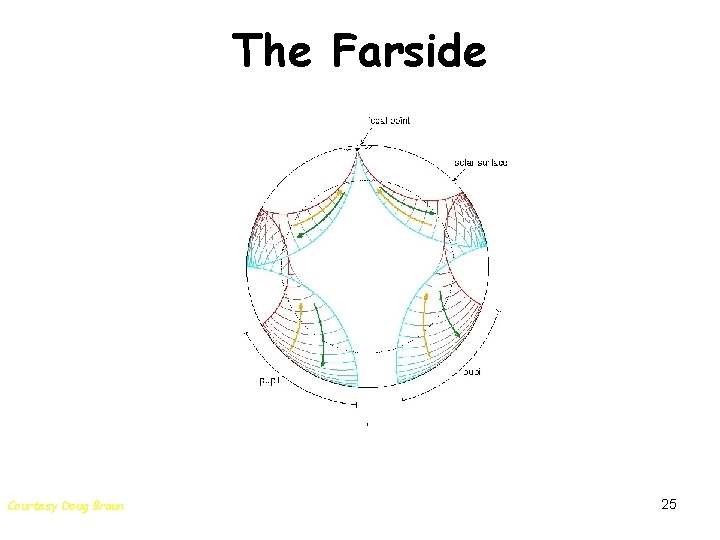
The Farside Courtesy Doug Braun 25

What we have learned, are learning, and hope to learn • Successes – The phenomenon itself, Neutrinos, J 2, Internal Rotation, Helium abundance, Opacities, Depth of Convection Zone, Structures, etc, etc… • Challenges – Origins of solar magnetism – Differential rotation, torsional oscillations, and meridional circulation – Sub-surface inhomogeneities – How all of this should manifest itself in other stars – How these tools can contribute to a predictive understanding of space weather. • Frontiers – Asteroseismology & G-modes 26

• Dynamo 27

Coexistence of magnetic fields consisting of widely different length scales, magnitudes and temporal scales Hierarchy in length scale: Ø Network fields ~ 100 km size Ø Sunspots, ephemeral regions, plage ~ 10000 -30000 km diameter Ø Unipolar regions ~ 100, 000 km extent Hierarchy in flux and/or field strength: Ø Spots, active regions, network fields ~ a few thousand Gauss Ø Plage ~ a few hundred Gauss Ø Large-scale diffuse fields ~ a few tens of Gauss Hierarchy in temporal variations: Ø Persistent, cyclic features: butterfly diagrams, polar reversal, active longitudes Ø Random features: small-scale mixed-polarity turbulent fields 28

What is a dynamo? A dynamo is a process by which the magnetic field in an electrically conducting fluid is maintained against Ohmic dissipation 29

Let’s Build A Homopolar-disc Dynamo A copper disc that can rotate about its axis 30

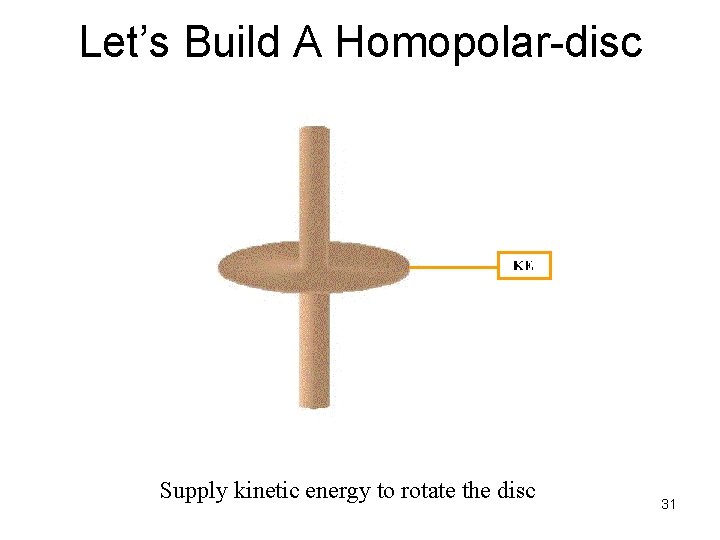
Let’s Build A Homopolar-disc Dynamo Supply kinetic energy to rotate the disc 31

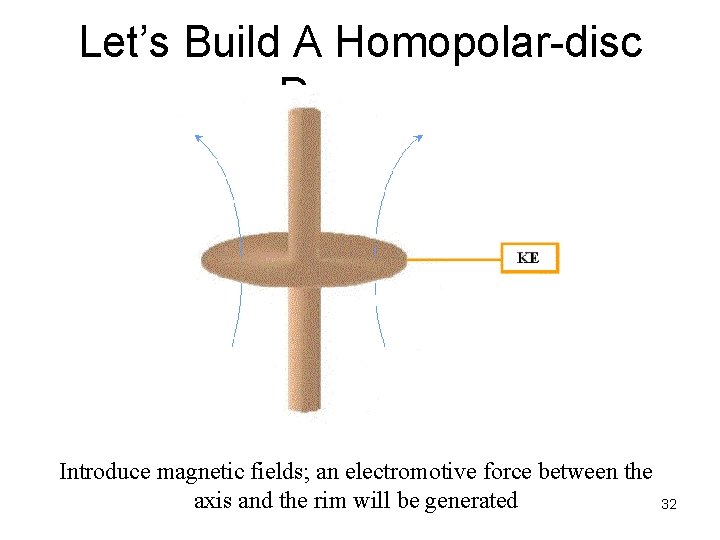
Let’s Build A Homopolar-disc Dynamo Introduce magnetic fields; an electromotive force between the axis and the rim will be generated 32

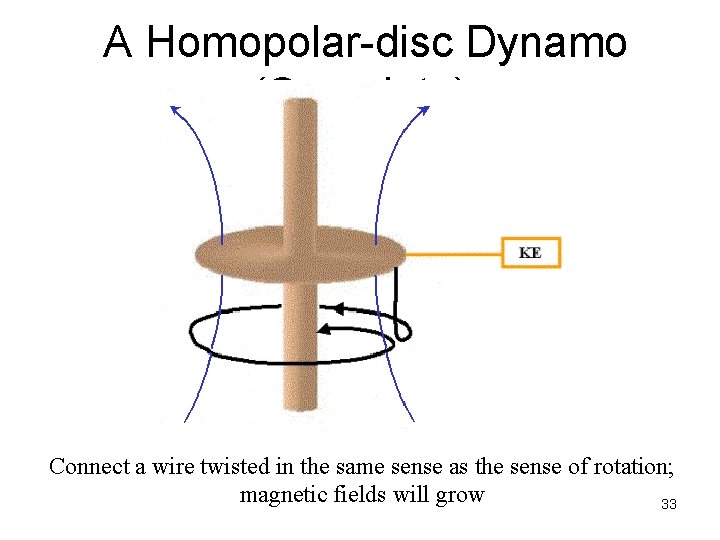
A Homopolar-disc Dynamo (Complete) Connect a wire twisted in the same sense as the sense of rotation; magnetic fields will grow 33

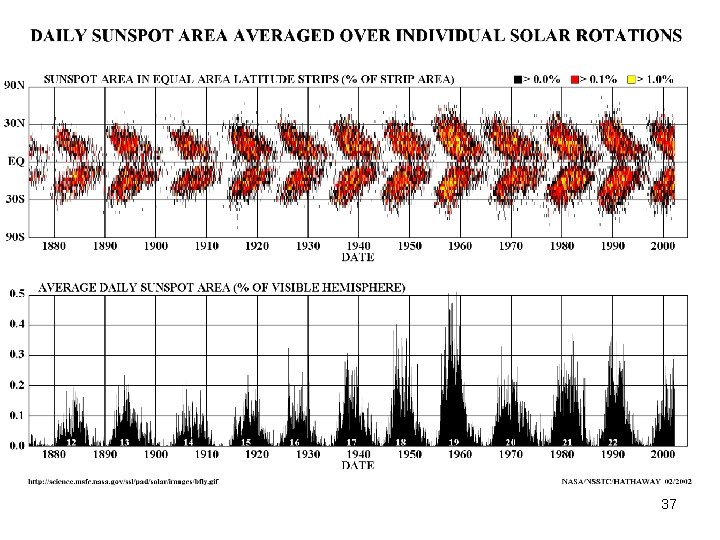
Observational signature for systematic, cyclic evolution of solar magnetic fields Courtesy: D. H. Hathaway Many evidences for coexistence of small-scale and large-scale dynamos 34

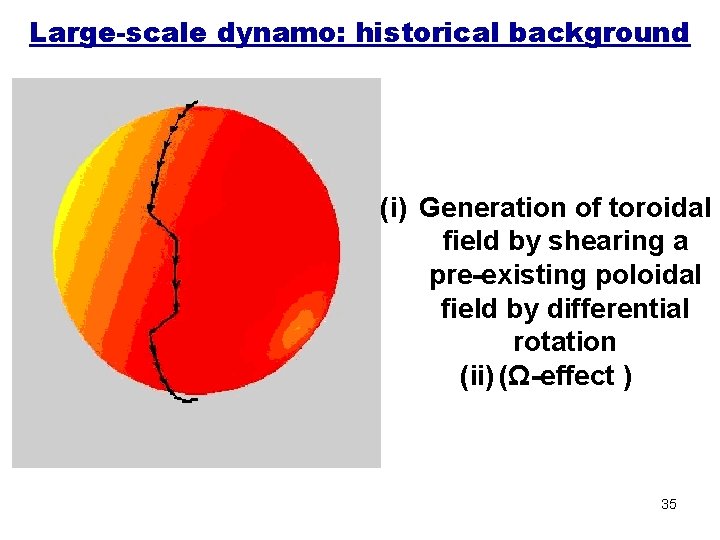
Large-scale dynamo: historical background (i) Generation of toroidal field by shearing a pre-existing poloidal field by differential rotation (ii) (Ω-effect ) 35

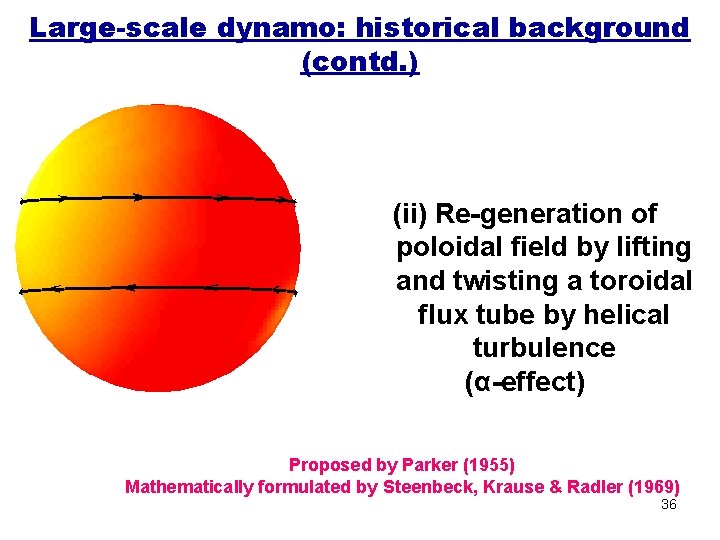
Large-scale dynamo: historical background (contd. ) (ii) Re-generation of poloidal field by lifting and twisting a toroidal flux tube by helical turbulence (α-effect) Proposed by Parker (1955) Mathematically formulated by Steenbeck, Krause & Radler (1969) 36

37

Large-scale dynamo: historical background (contd. ) • In 1960’s and 70’s, equatorward propagating dynamo wave was obtained by assuming a radial differential rotation increasing inward throughout the convection zone. • Sunspots were identified as that formed from strong toroidal flux tubes which rise to the surface due to their magnetic buoyancy • Equatorward migration of sunspot-belt was explained by an equatorward propagating dynamo wave for the subsurface toroidal fields Equatorward propagation of dynamo wave was obtained by satisfying Parker-Yoshimura Sign Rule; α dΩ/dr < 0, In North-hemisphere 38

Historical Background (contd. ) • But, In 1980’s, helioseismic analysis inferred that there is no radial shear in the convection zone, and the strong radial shear at or below the base of the convection zone is decreasing inward at sunspot latitudes. (Courtesy: Thierry Corbard) Therefore, Convection Zone Dynamos Do Not Work With Solar-like Ω 39

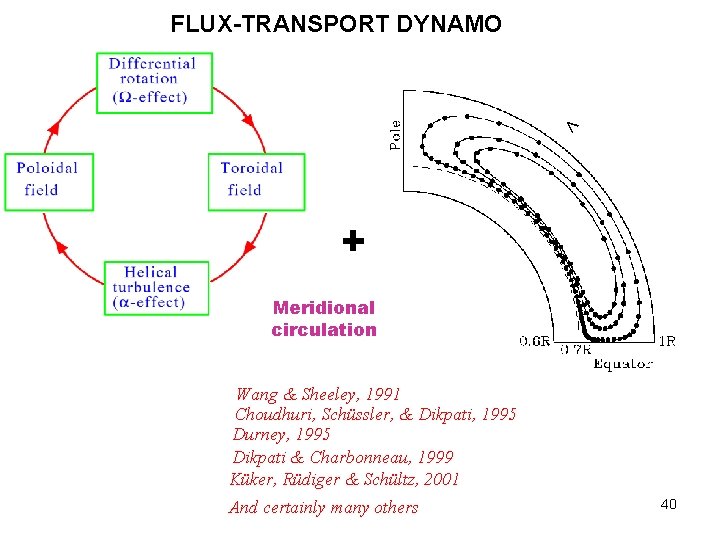
FLUX-TRANSPORT DYNAMO < + Meridional circulation Wang & Sheeley, 1991 Choudhuri, Schüssler, & Dikpati, 1995 Durney, 1995 Dikpati & Charbonneau, 1999 Küker, Rüdiger & Schültz, 2001 And certainly many others 40

Mathematical Formulation r MHD approximation (i. e. electromagnetic variations are nonrelativist xwell’s equations + generalized Ohm’s law lead to induction equation (1) plying mean-field theory to (1), we obtain the dynamo equation as, (2) Differential rotation and meridional circulation Diffusion (turbulent + molecular) Displacing and twisting effect by kinetic helicity 41

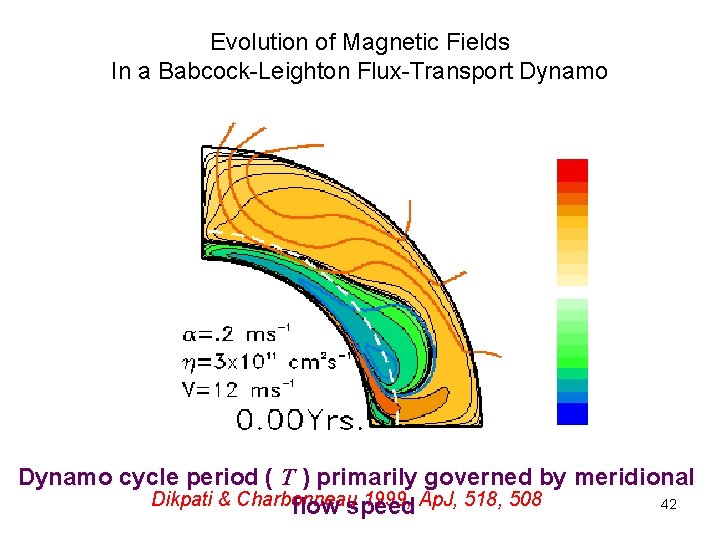
Evolution of Magnetic Fields In a Babcock-Leighton Flux-Transport Dynamo cycle period ( T ) primarily governed by meridional Dikpati & Charbonneau 1999, Ap. J, 518, 508 42 flow speed

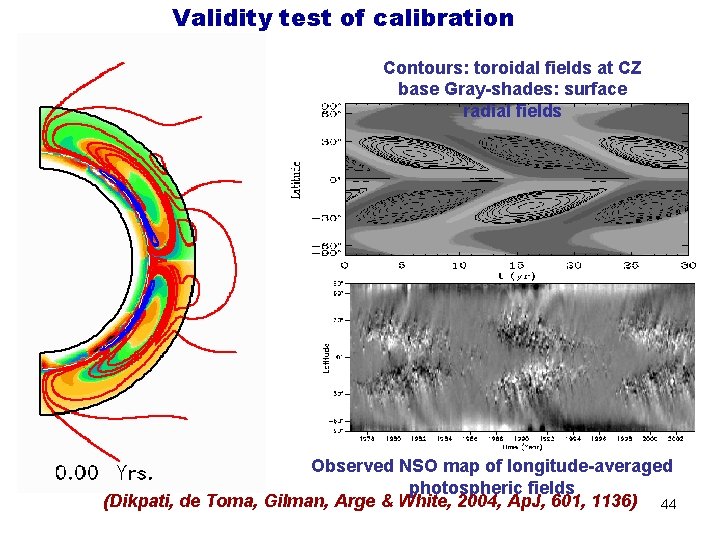
Validity test of calibration Contours: toroidal fields at CZ base Gray-shades: surface radial fields Observed NSO map of longitude-averaged photospheric fields (Dikpati, de Toma, Gilman, Arge & White, 2004, Ap. J, 601, 1136) 44

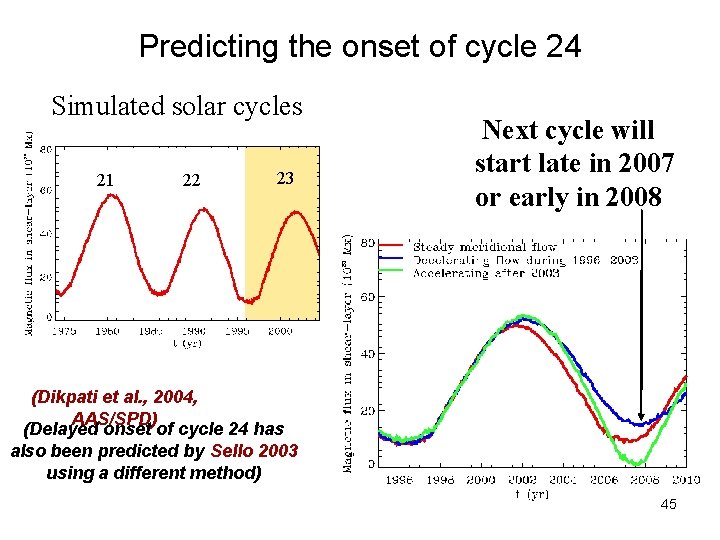
Predicting the onset of cycle 24 Simulated solar cycles 21 22 23 Next cycle will start late in 2007 or early in 2008 (Dikpati et al. , 2004, AAS/SPD) (Delayed onset of cycle 24 has also been predicted by Sello 2003 using a different method) 45

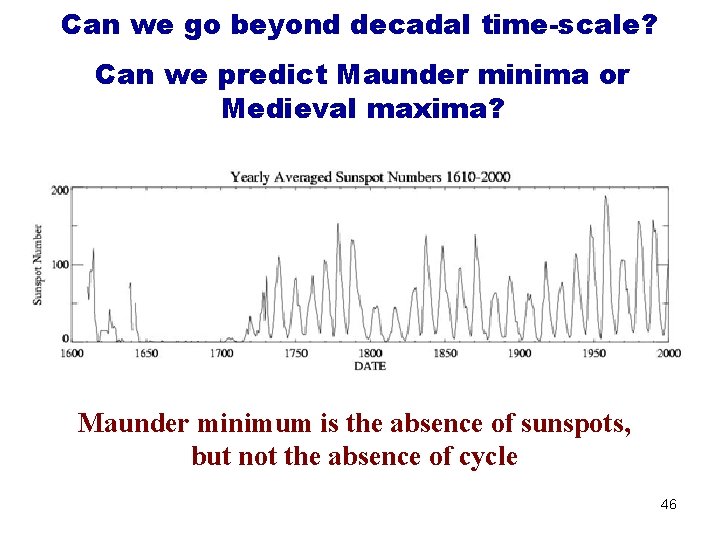
Can we go beyond decadal time-scale? Can we predict Maunder minima or Medieval maxima? Maunder minimum is the absence of sunspots, but not the absence of cycle 46

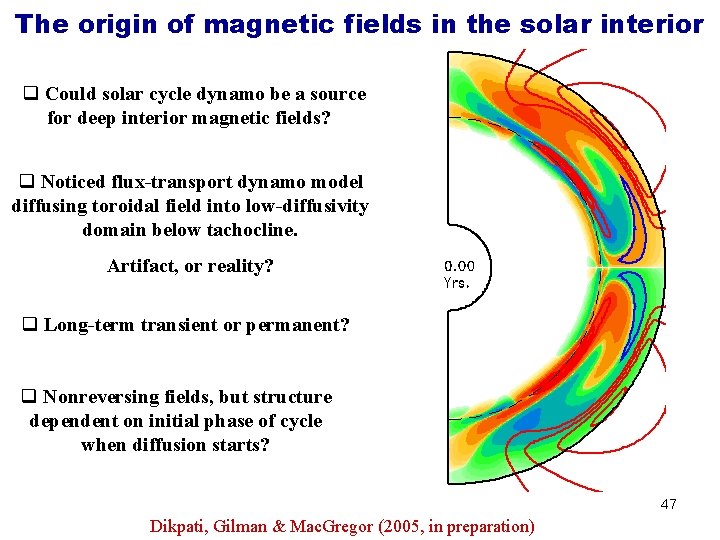
The origin of magnetic fields in the solar interior q Could solar cycle dynamo be a source for deep interior magnetic fields? q Noticed flux-transport dynamo model diffusing toroidal field into low-diffusivity domain below tachocline. Artifact, or reality? q Long-term transient or permanent? q Nonreversing fields, but structure dependent on initial phase of cycle when diffusion starts? 47 Dikpati, Gilman & Mac. Gregor (2005, in preparation)