Space Vector Modulation SVM PWM Voltage Source Inverter

Space Vector Modulation (SVM)

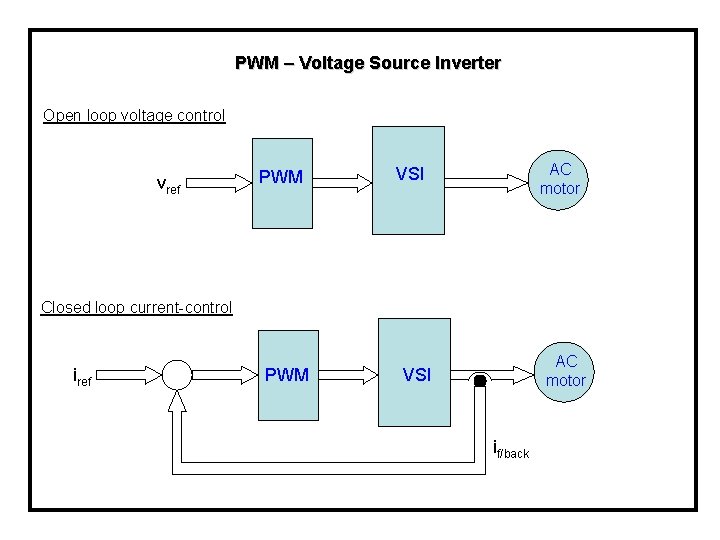
PWM – Voltage Source Inverter Open loop voltage control vref PWM AC motor VSI Closed loop current-control iref PWM AC motor VSI if/back

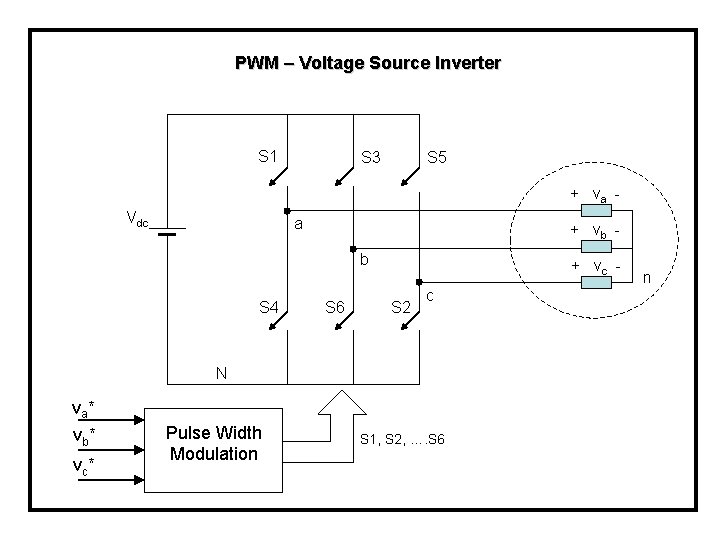
PWM – Voltage Source Inverter S 1 S 3 S 5 + va - Vdc a + vb b S 4 S 6 + vc S 2 c N va* vb* vc* Pulse Width Modulation S 1, S 2, …. S 6 n

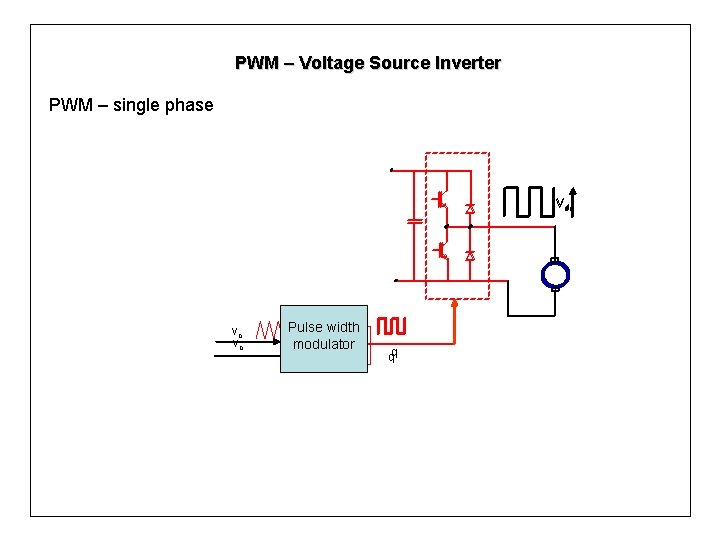
PWM – Voltage Source Inverter PWM – single phase Vdc dc vc vc v. Pulse width tri modulator qq

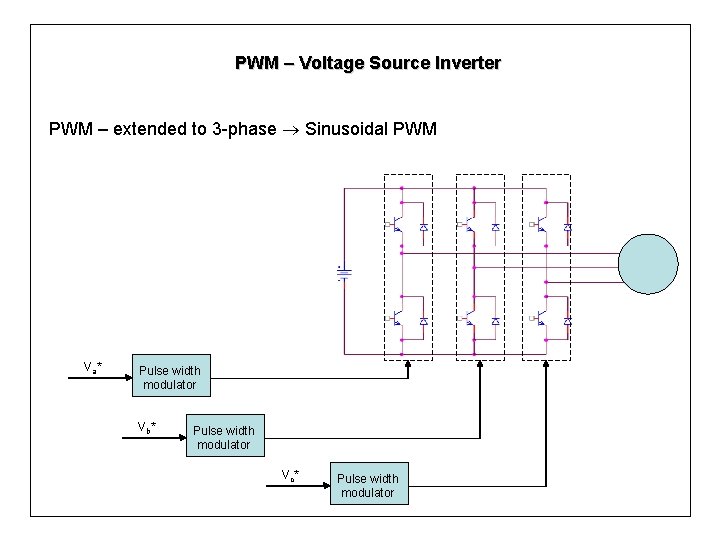
PWM – Voltage Source Inverter PWM – extended to 3 -phase Sinusoidal PWM Va* Pulse width modulator Vb* Pulse width modulator Vc * Pulse width modulator

PWM – Voltage Source Inverter SPWM – covered in undergraduate course or PE system (MEP 1532) In MEP 1422 we’ll look at Space Vector Modulation (SVM) – mostly applied in AC drives

Space Vector Modulation Definition: Space vector representation of a three-phase quantities xa(t), xb(t) and xc(t) with space distribution of 120 o apart is given by: a = ej 2 /3 = cos(2 /3) + jsin(2 /3) a 2 = ej 4 /3 = cos(4 /3) + jsin(4 /3) x – can be a voltage, current or flux and does not necessarily has to be sinusoidal

Space Vector Modulation

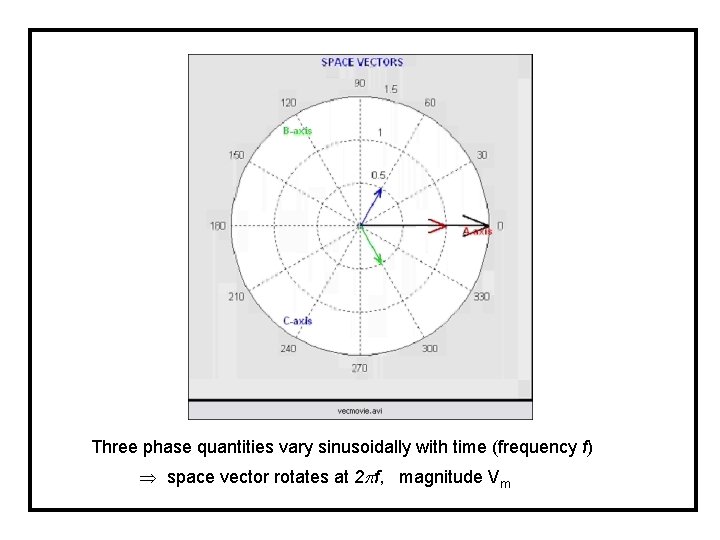
Space Vector Modulation Let’s consider 3 -phase sinusoidal voltage: va(t) = Vmsin( t) vb(t) = Vmsin( t - 120 o) vc(t) = Vmsin( t + 120 o)

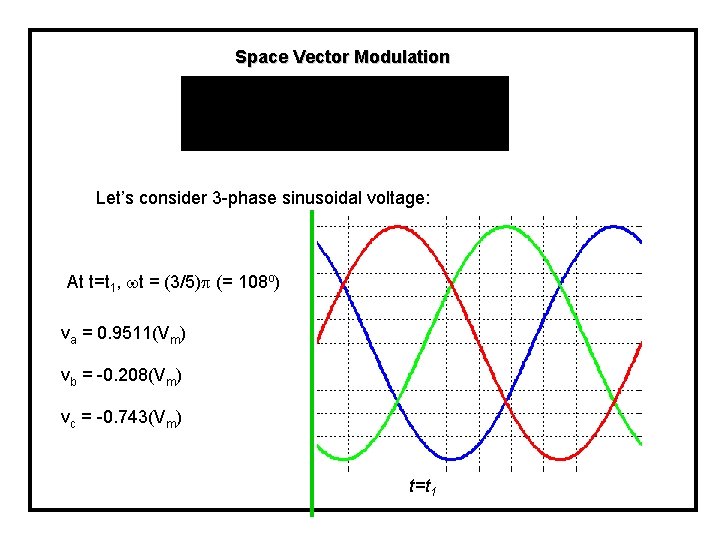
Space Vector Modulation Let’s consider 3 -phase sinusoidal voltage: At t=t 1, t = (3/5) (= 108 o) va = 0. 9511(Vm) vb = -0. 208(Vm) vc = -0. 743(Vm) t=t 1

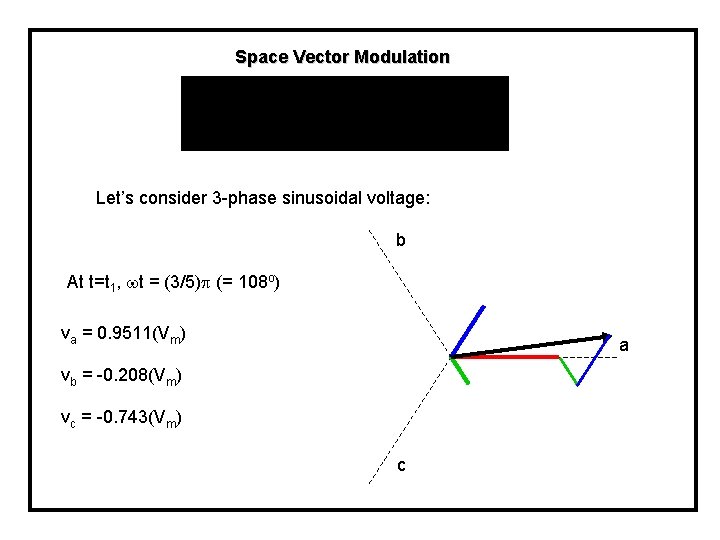
Space Vector Modulation Let’s consider 3 -phase sinusoidal voltage: b At t=t 1, t = (3/5) (= 108 o) va = 0. 9511(Vm) a vb = -0. 208(Vm) vc = -0. 743(Vm) c

Three phase quantities vary sinusoidally with time (frequency f) space vector rotates at 2 f, magnitude Vm

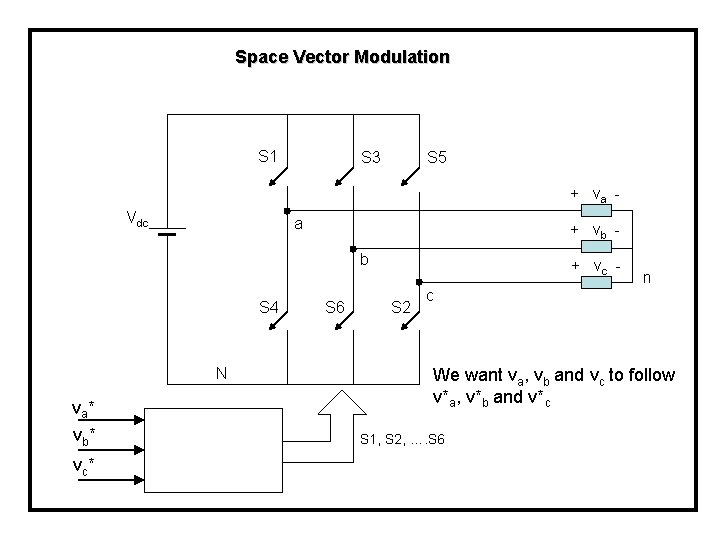
Space Vector Modulation How could we synthesize sinusoidal voltage using VSI ?

Space Vector Modulation S 1 S 3 S 5 + va - Vdc a + vb b S 4 N va* vb* vc* S 6 + vc S 2 n c We want va, vb and vc to follow v*a, v*b and v*c S 1, S 2, …. S 6

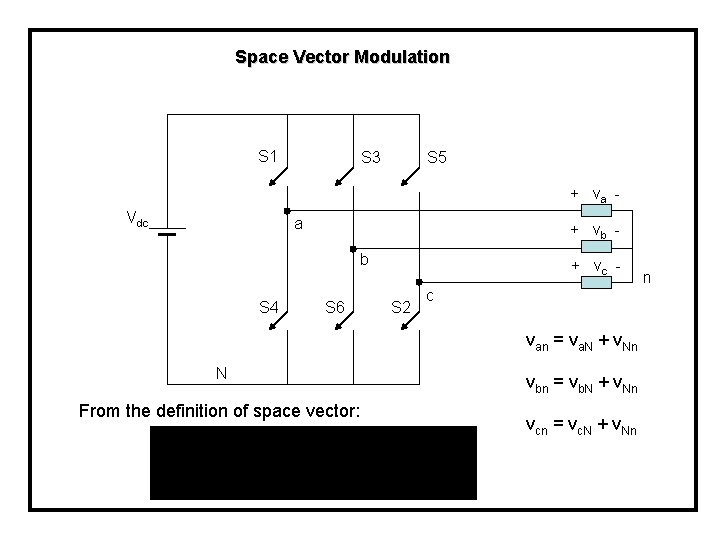
Space Vector Modulation S 1 S 3 S 5 + va - Vdc a + vb b S 4 S 6 + vc S 2 c van = va. N + v. Nn N From the definition of space vector: vbn = vb. N + v. Nn vcn = vc. N + v. Nn n

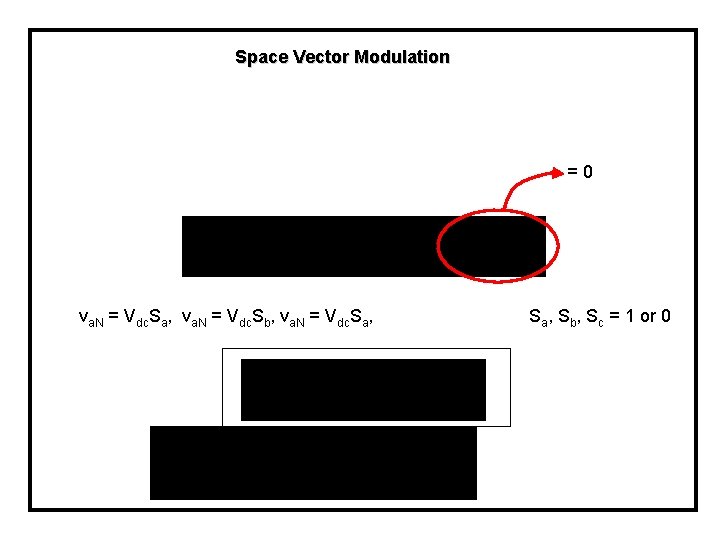
Space Vector Modulation =0 va. N = Vdc. Sa, va. N = Vdc. Sb, va. N = Vdc. Sa, Sb, Sc = 1 or 0

Space Vector Modulation Sector 2 [010] V 3 [110] V 2 (1/ 3)Vdc Sector 3 Sector 1 [100] V 1 [011] V 4 (2/3)Vdc Sector 4 Sector 6 [001] V 5 Sector 5 [101] V 6

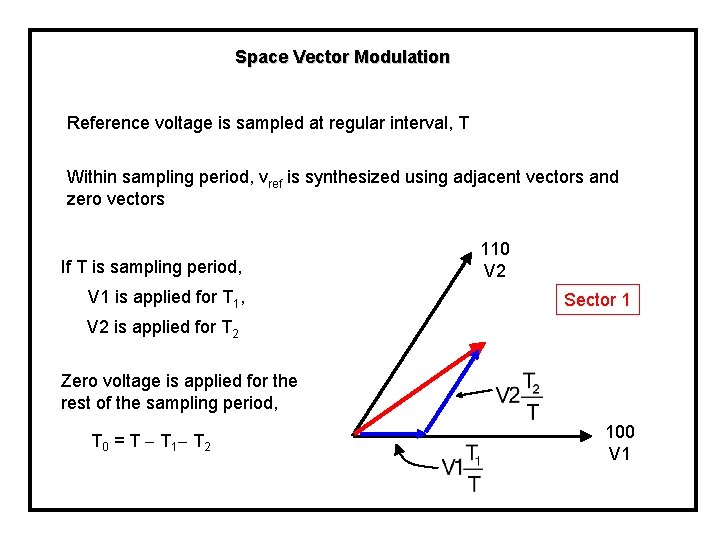
Space Vector Modulation Reference voltage is sampled at regular interval, T Within sampling period, vref is synthesized using adjacent vectors and zero vectors If T is sampling period, V 1 is applied for T 1, 110 V 2 Sector 1 V 2 is applied for T 2 Zero voltage is applied for the rest of the sampling period, T 0 = T T 1 T 2 100 V 1

Space Vector Modulation Reference voltage is sampled at regular interval, T Within sampling period, vref is synthesized using adjacent vectors and zero vectors T 0/2 T 1 V 0 If T is sampling period, V 1 is applied for T 1, T 2 T 0/2 V 1 V 2 V 7 va V 2 is applied for T 2 vb Zero voltage is applied for the rest of the sampling period, T 0 = T T 1 T 2 vc T Vref is sampled T

Space Vector Modulation How do we calculate T 1, T 2, T 0 and T 7? They are calculated based on volt-second integral of vref

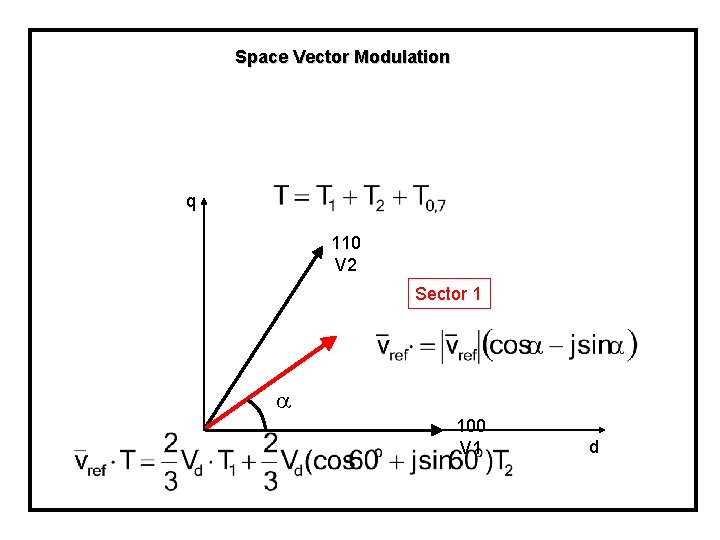
Space Vector Modulation q 110 V 2 Sector 1 100 V 1 d

Space Vector Modulation Solving for T 1, T 2 and T 0, 7 gives: where

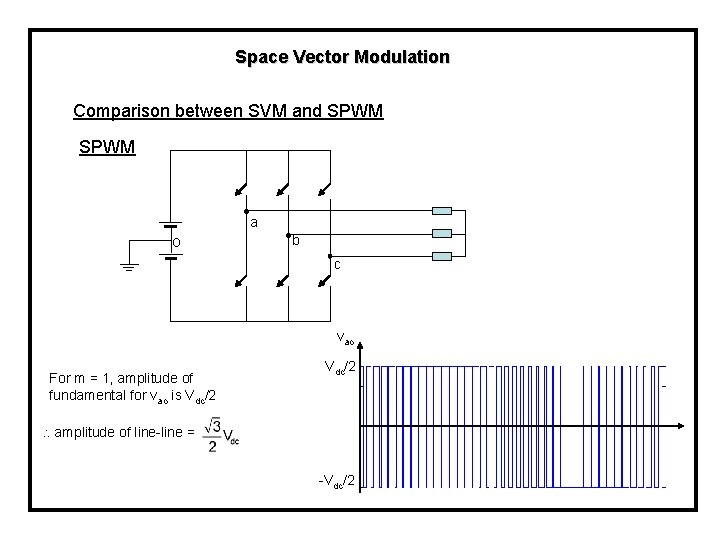
Space Vector Modulation Comparison between SVM and SPWM a o b c vao For m = 1, amplitude of fundamental for vao is Vdc/2 amplitude of line-line = -Vdc/2

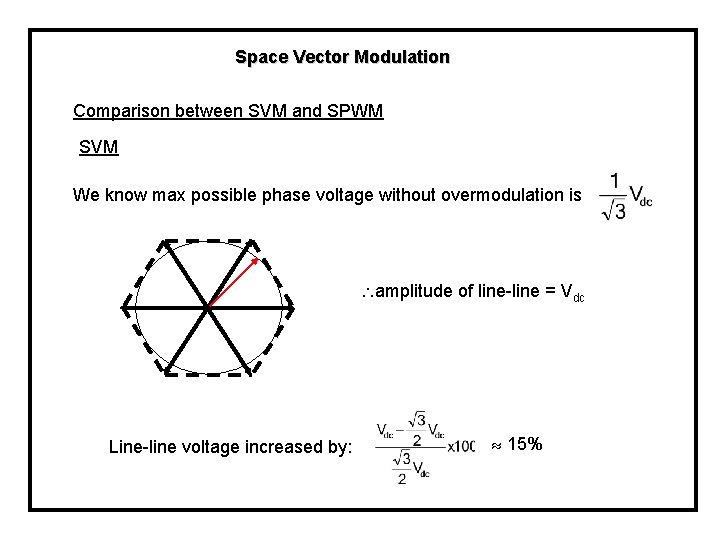
Space Vector Modulation Comparison between SVM and SPWM SVM We know max possible phase voltage without overmodulation is amplitude of line-line = Vdc Line-line voltage increased by: 15%