Space Physics and Space Weather Space empty volume






























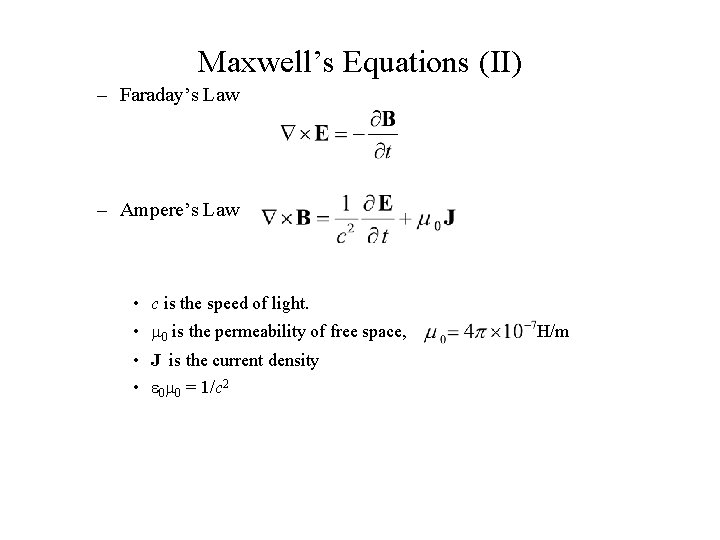
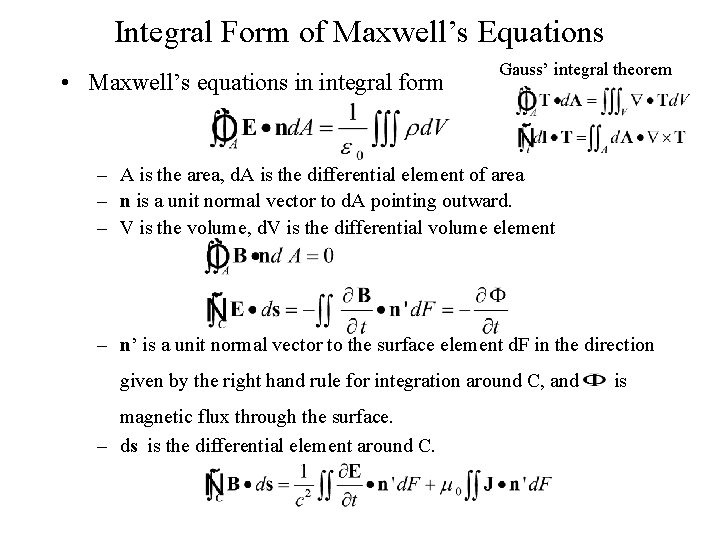















- Slides: 48

Space Physics and Space Weather • Space: “empty” volume between bodies (solid bodies are excluded) • Space physics: space within solar system (astrophysics is not space physics) • Solar-terrestrial relations: space physics focused on solar wind and terrestrial space • Space plasma physics: application of plasma physics to space • Space physics: Coriolis force and gravity not important (unless noted) • Space weather: space physics applications. Space phenomena that endanger space assets and applications and human in space • Space physics: electromagnetic field + charged particles • Require significant math: – Working on but not solving partial differential equations in this class – Vector operations • Require: electromagnetics (additional reading may help)

Regions in Space • Solar wind (sun’s atmosphere, but not bonded by gravity): plasma (ions and electrons in equal number but not attached to each other) stream flows out continuously, but with variations, from the sun with extremely high speeds into the interplanetary space. Note: in space, all ions are positively charged. • Formation of the magnetosphere: the solar wind deflected by the geomagnetic field. • Magnetopause: the boundary separates the magnetosphere from the solar wind (crucial for any solar wind entry). • Bow shock: standing upstream of the magnetopause, because the solar wind is highly supersonic. • Magnetosheath: the region between the bow shock and the magnetopause.


Regions in Space, cont. • Magnetotail: the magnetosphere is stretched by the solar wind on the nightside. • Radiation belts: where most energetic particles are trapped, (major issue for space mission safety). • Plasmasphere: inner part of magnetosphere with higher plasma density of ionospheric origin. • Ionosphere: (80 ~ 1000 km) regions of high density of charged particles of earth origin. • Thermosphere: (> 90 km) neutral component of the same region as the ionosphere. The temperature can be greater than 1000 K.

Space Weather Phenomena • Magnetic storms (hurricanes in space) • Global-scale long-lasting geomagnetic disturbances • Magnetic substorms (tornadoes in space) • Impulsive geomagnetic disturbances • Auroras (rains from space) • Enhanced energetic particle precipitations associated with storms/substorms • Ionospheric plasma density disturbances (fog? ) • Destruction of the layered structure of the ionosphere. • Enhanced extremely high-energy particle fluxes (hails? )

Evidence for Space Processes • Aurora: emissions caused by high energy charged particle precipitation into the upper atmosphere from space. • Geomagnetic field: caused by electric currents below the earth’s surface. • Geomagnetic storm/substorm: period of large geomagnetic disturbances. • Periodicity of magnetic storms: ~ 27 days. • Rotation of the Sun: 26 ~ 27 days.

• Space physics started with observations of the aurora. – Old Testament references to auroras. – Greek literature speaks of “moving accumulations of burning clouds” – Chinese literature has references to auroras prior to 2000 BC

– Galileo theorized that aurora is caused by air rising out of the Earth’s shadow to where it could be illuminated by sunlight. (Note he also coined the name aurora borealis meaning “northern dawn”. ) – Descartes thought they are reflections from ice crystals. – Halley suggested that auroral phenomena are ordered by the Earth’s magnetic field. – In 1731 the French philosopher de Mairan suggested they are connected to the solar atmosphere.

• By the 11 th century the Chinese had learned that a magnetic needle points north-south. • By the 12 th century the European records mention the compass. • That there was a difference between true north and the direction of the compass needle (declination) was known by the 16 th century. • William Gilbert (1600) realized that the field was dipolar. • In 1698 Edmund Halley organized the first scientific expedition to map the field in the Atlantic Ocean.

Plasma • A plasma is an electrically neutral ionized gas. – The Sun is a plasma – Interplanetary medium: the space between the Sun and the Earth is “filled” with a plasma. – The Earth is surrounded by plasmas: magnetosphere, ionosphere. – Planetary magnetospheres, ionospheres – A stroke of lightning forms plasma – Over 99% of the Universe is plasma. • Although neutral a plasma is composed of charged particleselectric and magnetic forces are critical to understand plasmas. • Plasma physics: three descriptions – Single particle theory – Fluid theory – Kinetic theory

Forces on charged particles (single particle theory) – Electric force – Magnetic force – Lorentz force – Neutral forces FE = q. E FB = qvx. B F = q. E + qvx. B Fg =mg,

Single Particle Motion • SI Units –mass (m) - kg –length (l) - m –time (t) - s –electric field (E) - V/m –magnetic field (B) - T –velocity (v) - m/s –Fg stands for non-electromagnetic forces (e. g. gravity) - usually ignorable.

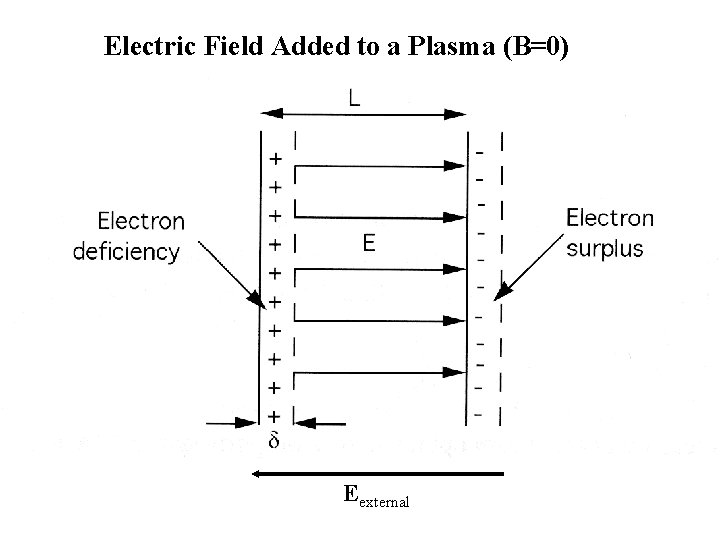
Electric Field Added to a Plasma (B=0) Eexternal

–If q is positive particle gyrates in left handed sense –If q is negative particle gyrates in a right handed sense






• Gyro motion – The gyro radius is a function of energy. – Energy of charged particles is usually given in electron volts (e. V) – Energy that a particle with the charge of an electron gets in falling through a potential drop of 1 Volt- 1 e. V = 1. 6 X 10 -19 Joules (J). • Energies in space plasmas go from electron Volts to kiloelectron Volts (1 ke. V = 103 e. V) to millions of electron Volts (1 me. V = 106 e. V) • Cosmic energies go to gigaelectron Volts ( 1 ge. V = 109 e. V). • The circular motion does no work on a particle Only the electric field can energize particles!




Pitch angle and magnetic moment

Single particle theory: guiding center drift • The electric field can modify the particles motion. – Assume but still uniform and Fg=0. – Frequently in space physics it is ok to set • Only can accelerate particles along • Positive particles go along and negative particles go along • Eventually charge separation wipes out – has a major effect on motion. • As particle gyrates it moves along and gains energy • Later in the circle it losses energy. • This causes different parts of the “circle” to have different radii - it doesn’t close on itself. • Drift velocity is perpendicular to and • No charge dependence, (electrons and ions move in the direction and speed) therefore no currents


Drift Motion: General Form • Any force capable of accelerating and decelerating charged particles can cause them to drift. – If the force is charge independent the drift motion will depend on the sign of the charge and can form perpendicular currents.

Homework • Derive the magnitude of the Ex. B drift with physical understanding of it. • Explain the physical reasons for the displacement current in the Maxwell’s equation according to current conservation, the form of which needs to be derived. • 2. 13, 2. 15 (no (d) for under), 2. 16, 2. 18, 2. 4* • Errors in the book. – – – 2. 4, gamma => 1/gamma 2. 13, page 32, line 2 above the figure, del. B=-3 B/r 2. 15, alpha is a constant, not pitch angle. 2. 18, 10^6 km, not used. 2. 18: assume parallel for curvature drift and perpendicular for gradient drift – 2. 18, Hint: radius of curvature: calculus.

Lecture II

Electric and Magnetic Fields: Simple situations • Single electric charge (monopole): – – Positive charge Negative charge Net charge E field (intensity): + => - • Electric dipole • No magnetic monopole. • Magnetic field (magnetic dipole) – – Magnet: N and S (pointing to), geomagnetic poles: located oppositely, B (mag flux density, including magnetization): N=>S (H: mag field intensity) current loop • E and B are chosen in plasma physics because of the Lorentz force.

Maxwell’s Equations • Maxwell’s equations – Poisson’s Equation (originally from Coulomb's law) • E is the electric field • is the electric charge density • 0 is the electric permittivity (8. 85 X 10 -12 Farad/m) • Positive charge starts electric field line • Negative charge ends the line. – Gauss Law (absence of magnetic monopoles) • B is the magnetic field • Magnetic field line has neither beginning nor end.
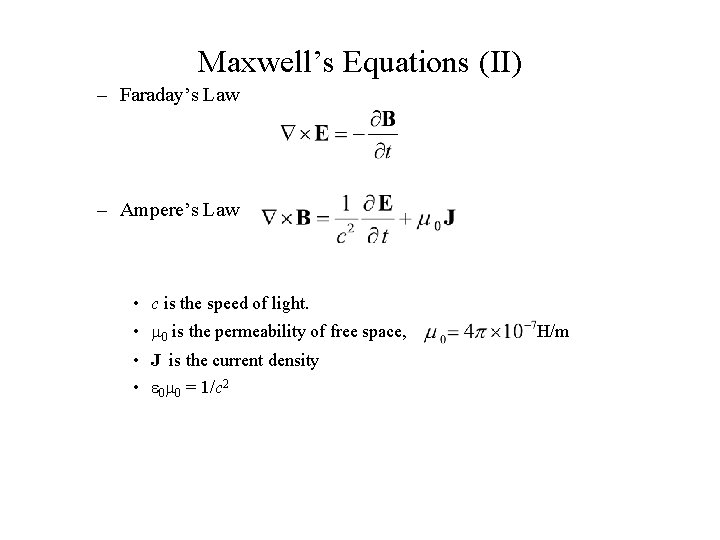
Maxwell’s Equations (II) – Faraday’s Law – Ampere’s Law • c is the speed of light. • 0 is the permeability of free space, • J is the current density • 0 0 = 1/c 2 H/m
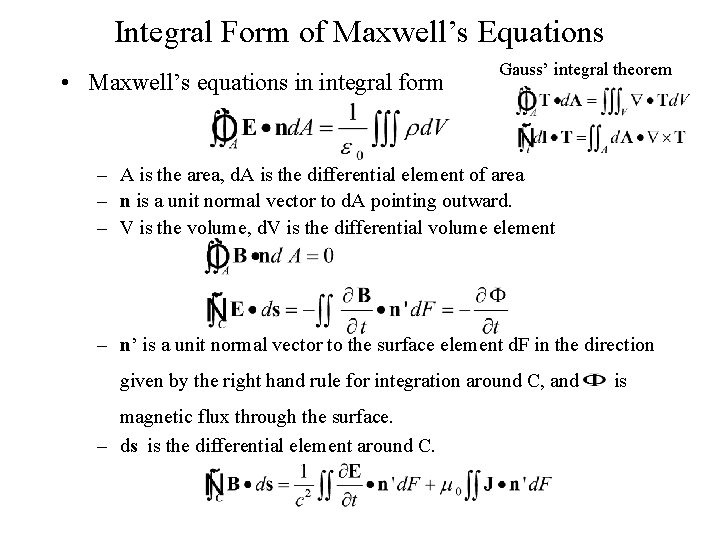
Integral Form of Maxwell’s Equations • Maxwell’s equations in integral form Gauss’ integral theorem – A is the area, d. A is the differential element of area – n is a unit normal vector to d. A pointing outward. – V is the volume, d. V is the differential volume element – n’ is a unit normal vector to the surface element d. F in the direction given by the right hand rule for integration around C, and magnetic flux through the surface. – ds is the differential element around C. is

Nonuniform B Field: Gradient B drift

Centrifugal Force: Curvature drift



Adiabatic Invariants

Magnetic mirrors The two components are related as required by the divergence-free of the magnetic field

On page 39, the magnetic mirror force, the equation 3 lines from (2. 79) misses a negative sign.


• The force is along B and away from the direction of increasing B. • If and kinetic energy must be conserved a decrease in must yield an increase in • Particles will turn around when

Magnetic bottle bounce period

• In general, the second adiabatic invariant – The integral of the parallel momentum over one complete bounce between mirrors is constant (as long as B doesn’t change much in a bounce). – Using conservation of energy and the first adiabatic invariant – If the field is a dipole their trajectories will take them around the planet and close on themselves.

• The third adiabatic invariant – As particles bounce they will drift because of gradient and curvature drift motion. – As long as the magnetic field doesn’t change much in the time required to drift around a planet the magnetic flux inside the orbit must be constant.


• Limitations on the invariants – is constant when there is little change in the field’s strength over a cyclotron path. – All invariants require that the magnetic field not change much in the time required to one cycle of motion where is the orbit period.

• The Concept of the Guiding Center – Separates the motion (v) of a particle into motion perpendicular (v ) and parallel ( v||) to the magnetic field. – To a good approximation the perpendicular motion can consist of a drift (u. D ) and the gyromotion ( v c) – Over long times the gyromotion is averaged out and the particle motion can be described by the guiding center motion consisting of the parallel motion and drift.