SPACE LATTICES Part of MATERIALS SCIENCE A Learners

SPACE LATTICES Part of MATERIALS SCIENCE & A Learner’s Guide ENGINEERING AN INTRODUCTORY E-BOOK Anandh Subramaniam & Kantesh Balani Materials Science and Engineering (MSE) Indian Institute of Technology, Kanpur- 208016 Email: anandh@iitk. ac. in, URL: home. iitk. ac. in/~anandh http: //home. iitk. ac. in/~anandh/E-book. htm

Space Lattice A lattice is also called a Space Lattice (or even Bravais Lattice in some contexts) An array of points in space such that every point has identical surroundings. Note: this is the formal definition of a lattice Whichever point in the lattice you ‘sit’ (position yourself), space should look identical to you. This automatically implies two properties of lattices In Euclidean space lattices are infinite (infinite array) Lattices ‘have translationalorperiodicity’ Translationally periodic arrangement of points in space is called a lattice* u We can have 1 D, 2 D or 3 D arrays (lattices) The motif associated with these lattices can themselves be 1 D, 2 D or 3 D ‘entities’. * this definition arises naturally from the first definition. Note: points are drawn with finite size for clarity in reality they are 0 D (zero dimensional). Auguste Bravais in 1847 showed that there are fourteen 3 D lattices and not fifteen. Moritz Ludwig Frankenheim had earlier listed 15 Lattices (over-counted by one).

1 D Lattices

1 D Lattices Construction of a 1 D lattice Let us construct a 1 D lattice starting with two points These points are shown as ‘finite’ circles for better ‘visibility’! The point on the right has one to the left and hence by the requirement of identical surrounding the one of the left should have one more to the left By a similar argument there should be one more to the left and one to the right This would lead to an infinite number of points The infinity on the sides would often be left out from schematics In 1 D spherical space a lattice can be finite!

1 D Lattices Starting with a point the lattice translation vector (basis vector) can generate the lattice Though this is called a lattice parameter it is better described as the unit cell parameter In 1 D there is only one kind of lattice. This lattice can be described by a single lattice parameter (a). In 1 D the action of a mirror operator is same as that of a 2 -fold or a inversion operator (Mirror 2 -fold Inversion). In 1 D the mirror and the 2 -fold axis reduce to a point. I. e. the mirror in 1 D is no longer a plane, but a point. Similarly, the 2 -fold axis is not a line, but a point. (Shown below for a two line segment object). In the 1 D lattice the mirrors are at lattice point (m 0) and midway between them (m½). Other symmetries (3 -fold, screw axis, etc. ) do not exist in 1 D. 1 To obtain a 1 D crystal this lattice has to be decorated with a motif. The unit cell for this lattice is a line segment of length a. Click here to see how symmetry operators generate the 1 D lattice Note: Basis vector should not be confused with the basis ( the motif)

How can make some 1 -D crystals out of the lattice we have constructed Click here

2 D Lattices

2 D Lattices 2 D lattices can be generated with two basis vectors They are infinite in two dimensions There are five distinct 2 D lattices: 1 Square 2 Rectangle 3 Centered Rectangle 4 120 Rhombus 5 Parallelogram (general) This aspect can be quite confusing Note that in the classification of lattices, we are considering the shape of the unit cell and the disposition of lattice points with respect to that unit cell (i. e. , “are there a lattice points only in the corners? ”, “is there lattice point at the centre also? ”). However, at the heart of the classification is the symmetry of the lattice. To simplify matters: In this set of slides we will NOT consider symmetries with translation built into them (e. g. glide reflection)

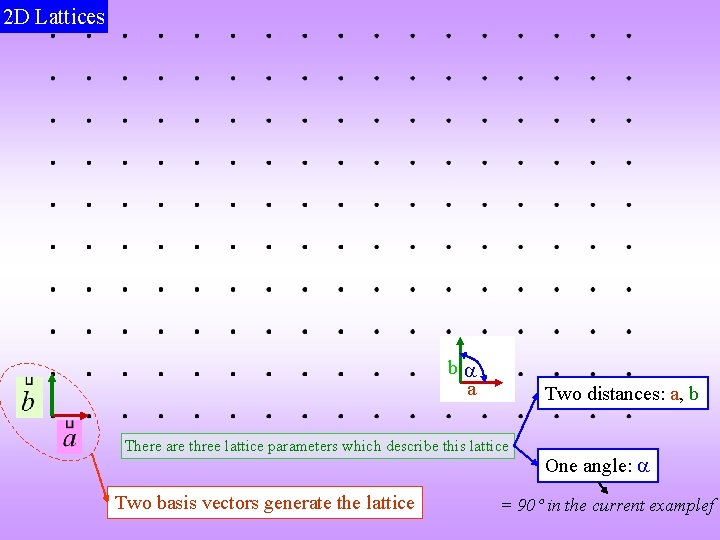
2 D Lattices b a Two distances: a, b There are three lattice parameters which describe this lattice Two basis vectors generate the lattice One angle: = 90 in the current examplef

Four (4) Unit Cell shapes in 2 D can be used for 5 lattices as follows: There are 3 lattice parameters in 2 D (two Square (a = b, = 90 ) distances and one included angle) Rectangle (a, b, = 90 ) 120 Rhombus (a = b, = 120 ) Though these are called lattice parameters it is better described as the unit cell parameters Parallelogram (general) (a, b, ) It is clear some of them require more parameters to describe than others. I. e. might exist constraints (amongst these parameters), which reduces the number of independent lattice parameters. Some of them have special constraints on the angle. Can we put them in some order? The next slide defines a parameter called ‘terseness’ to order them.

Progressive relaxation of the constraints on the lattice parameters amongst the FIVE 2 D lattice shapes Increasing number t • p’ = number of independent parameters = (p e) (discounting the number of =) • c = number of constraints (positive “= some number“) • t = terseness = (p c) (is a measure of the ‘expenditure’ on the parameters Square (p’ = 2, c = 2, t = 1) a=b = 90º Rhombus (p’ = 2, c = 2, t = 1) a=b = 120º Note how the Square and the Rhombus are in the same level Rectangle (p’ = 3, c = 1 , t = 2) a b = 90º Parallelogram (p’ = 3, c = 0 , t = 3) a b E. g. for Square: there are 3 parameters (p) and 1 “=“ amongst them (e) p’ = (p e) = (3 1) = 2

Now let us consider the 5 lattices one by one

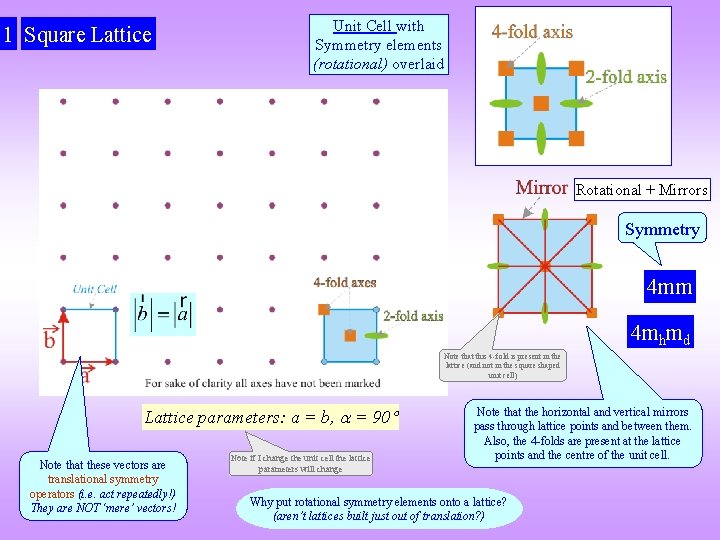
1 Square Lattice Unit Cell with Symmetry elements (rotational) overlaid Rotational + Mirrors Symmetry 4 mm 4 mhmd Note that this 4 -fold is present in the lattice (and not in the square shaped unit cell) Lattice parameters: a = b, = 90 Note that these vectors are translational symmetry operators (i. e. act repeatedly!) They are NOT ‘mere’ vectors! Note if I change the unit cell the lattice parameters will change Note that the horizontal and vertical mirrors pass through lattice points and between them. Also, the 4 -folds are present at the lattice points and the centre of the unit cell. Why put rotational symmetry elements onto a lattice? (aren’t lattices built just out of translation? )

A note on the symmetry Note that the periodicity of the lattice is a & b but the periodicity of the mirrors along x, y are a/2 and b/2 Rotational + Mirrors Symmetry 4 mm This (4 mm) is the symmetry of the square lattice. Crystals based on the square lattice can have lower symmetry than the lattice itself. If the crystal based on the square lattice has 4 mm or 4 symmetry then the crystal will be called a Square Crystal (else not).

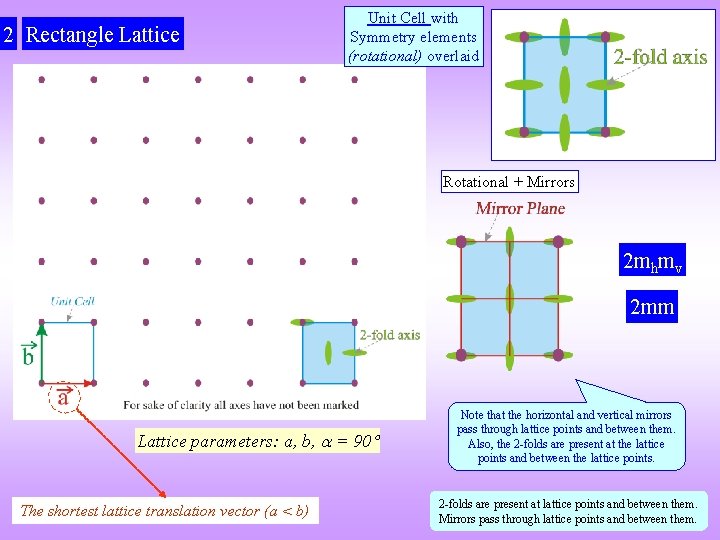
2 Rectangle Lattice Unit Cell with Symmetry elements (rotational) overlaid Rotational + Mirrors 2 mhmv 2 mm Lattice parameters: a, b, = 90 The shortest lattice translation vector (a < b) Note that the horizontal and vertical mirrors pass through lattice points and between them. Also, the 2 -folds are present at the lattice points and between the lattice points. 2 -folds are present at lattice points and between them. Mirrors pass through lattice points and between them.

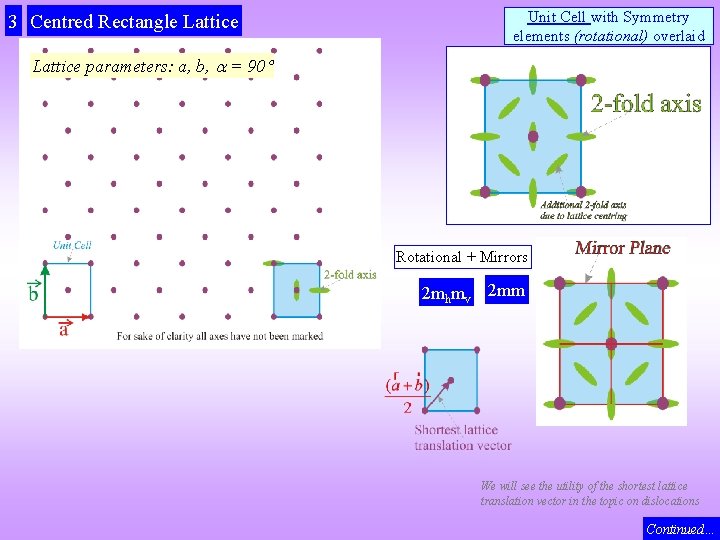
3 Centred Rectangle Lattice Unit Cell with Symmetry elements (rotational) overlaid Lattice parameters: a, b, = 90 Rotational + Mirrors 2 mhmv 2 mm We will see the utility of the shortest lattice translation vector in the topic on dislocations Continued…

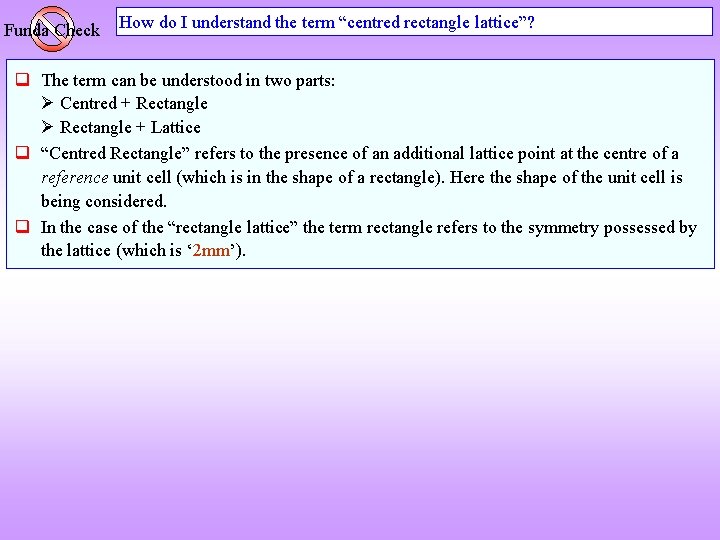
Funda Check How do I understand the term “centred rectangle lattice”? The term can be understood in two parts: Centred + Rectangle + Lattice “Centred Rectangle” refers to the presence of an additional lattice point at the centre of a reference unit cell (which is in the shape of a rectangle). Here the shape of the unit cell is being considered. In the case of the “rectangle lattice” the term rectangle refers to the symmetry possessed by the lattice (which is ‘ 2 mm’).

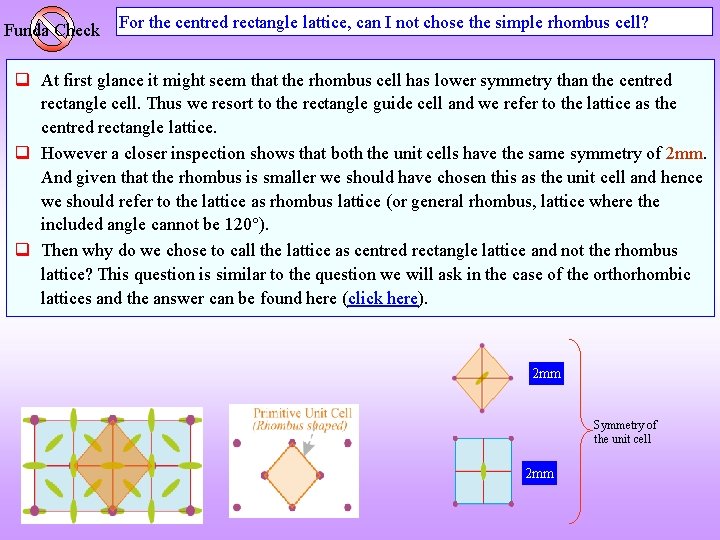
Funda Check For the centred rectangle lattice, can I not chose the simple rhombus cell? At first glance it might seem that the rhombus cell has lower symmetry than the centred rectangle cell. Thus we resort to the rectangle guide cell and we refer to the lattice as the centred rectangle lattice. However a closer inspection shows that both the unit cells have the same symmetry of 2 mm. And given that the rhombus is smaller we should have chosen this as the unit cell and hence we should refer to the lattice as rhombus lattice (or general rhombus, lattice where the included angle cannot be 120 ). Then why do we chose to call the lattice as centred rectangle lattice and not the rhombus lattice? This question is similar to the question we will ask in the case of the orthorhombic lattices and the answer can be found here (click here). 2 mm Symmetry of the unit cell 2 mm

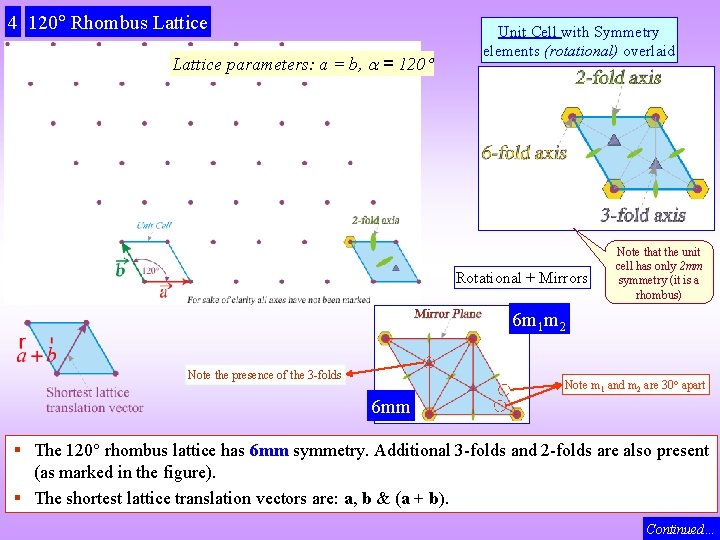
4 120 Rhombus Lattice parameters: a = b, = 120 Unit Cell with Symmetry elements (rotational) overlaid Rotational + Mirrors Note that the unit cell has only 2 mm symmetry (it is a rhombus) 6 m 1 m 2 Note the presence of the 3 -folds Note m 1 and m 2 are 30 apart 6 mm § The 120 rhombus lattice has 6 mm symmetry. Additional 3 -folds and 2 -folds are also present (as marked in the figure). § The shortest lattice translation vectors are: a, b & (a + b). Continued…

§ Note: this 120 rhombus lattice is ‘endowed’ with a very specific angle. § A general rhombus where α 120 will be listed under centred rectangle lattice. Note: the rhombus shaped unit cell itself does not have a 6 -fold symmetry. This implies that the rhombus shaped unit cell has ‘much’ lower symmetry than the lattice. General rhombus centred rectangle Q) Why can’t I use the rectangle unit cell? Like the way I did for the centred rectangle lattice (where again the rhombus unit cell was available). A) In principle one can use this rectangle cell with a lattice centering. A compound hexagonal cell (not a unit cell) can be made with this 120 rhombus cell (as in the next slide), which has 6 -fold symmetry. § Summary: For the lattice with 6 -fold symmetry we use the 120 rhombus UC. For a ‘rhombic’ lattice with a general angle, we use the centred rectangle unit cell. Q: I have seen a different representation of the same unit cell WITHOUT the 6 -folds. How come? Continued…

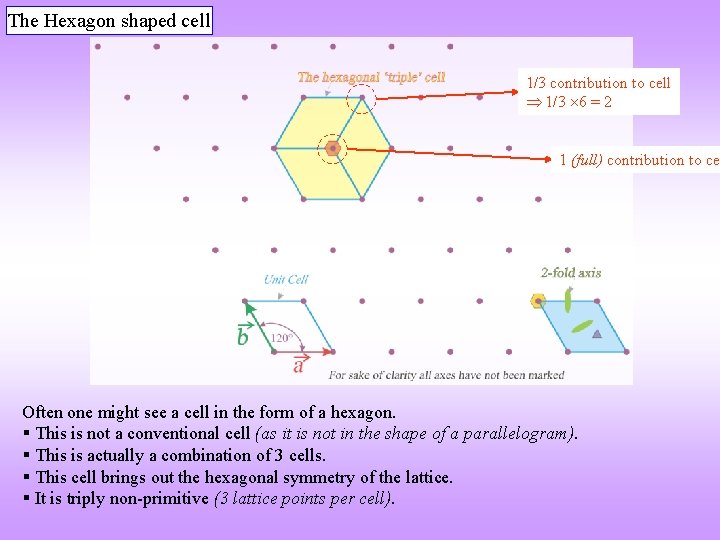
The Hexagon shaped cell 1/3 contribution to cell 1/3 6 = 2 1 (full) contribution to cel Often one might see a cell in the form of a hexagon. § This is not a conventional cell (as it is not in the shape of a parallelogram). § This is actually a combination of 3 cells. § This cell brings out the hexagonal symmetry of the lattice. § It is triply non-primitive (3 lattice points per cell).

5 Parallelogram/Oblique Lattice Unit Cell with Symmetry elements overlaid 2 Lattice parameters: a, b, 90 There are no mirrors in parallelogram lattice § § A general parallelogram (or often called a oblique) lattice has only 2 -fold symmetry elements. The 2 -folds are present at the lattice points and centres of edges and faces of the unit cell. The included angle cannot be 90 (as this will lead to a rectangle lattice). In effect the rectangle lattice and the oblique lattice have the same symmetry but ‘somehow’ 90 is ‘special’ !!!

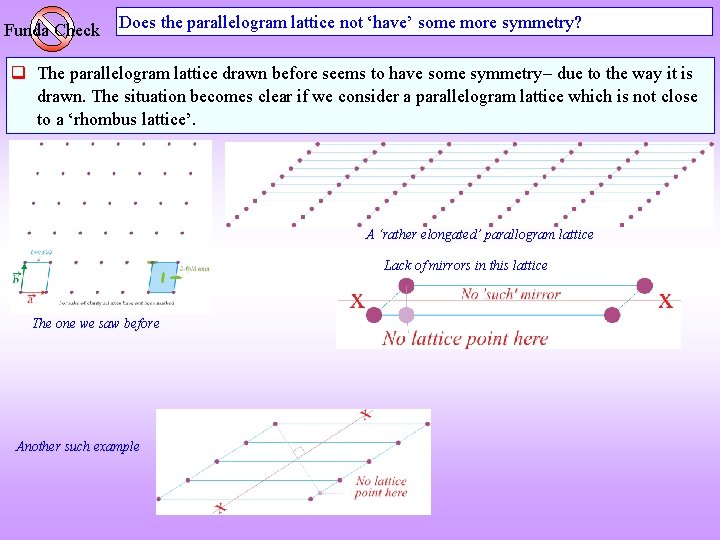
Funda Check Does the parallelogram lattice not ‘have’ some more symmetry? The parallelogram lattice drawn before seems to have some symmetry due to the way it is drawn. The situation becomes clear if we consider a parallelogram lattice which is not close to a ‘rhombus lattice’. A ‘rather elongated’ parallogram lattice Lack of mirrors in this lattice The one we saw before Another such example

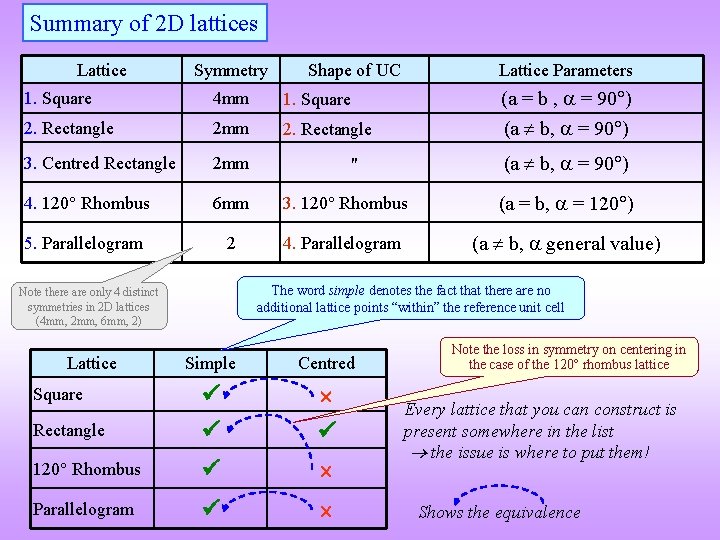
Summary of 2 D lattices Lattice Symmetry Shape of UC Lattice Parameters (a = b , = 90 ) (a b, = 90 ) 1. Square 4 mm 1. Square 2. Rectangle 2 mm 2. Rectangle 3. Centred Rectangle 2 mm 4. 120 Rhombus 6 mm 3. 120 Rhombus (a = b, = 120 ) 5. Parallelogram 2 4. Parallelogram (a b, general value) The word simple denotes the fact that there are no additional lattice points “within” the reference unit cell Note there are only 4 distinct symmetries in 2 D lattices (4 mm, 2 mm, 6 mm, 2) Lattice Simple Centred Rectangle 120 Rhombus Parallelogram Square (a b, = 90 ) " Note the loss in symmetry on centering in the case of the 120 rhombus lattice Every lattice that you can construct is present somewhere in the list the issue is where to put them! Shows the equivalence

Why are some of the possible 2 D lattices missing? We had seen that there is a rectangle lattice and a centred rectangle lattice. The natural question which comes to mind is that why are there no centred square, centred rhombus and centred parallelogram lattices? We have already answered the question regarding the centred square lattice. (However, we will repeat the answer here again). We will also answer the question for the other cases now.

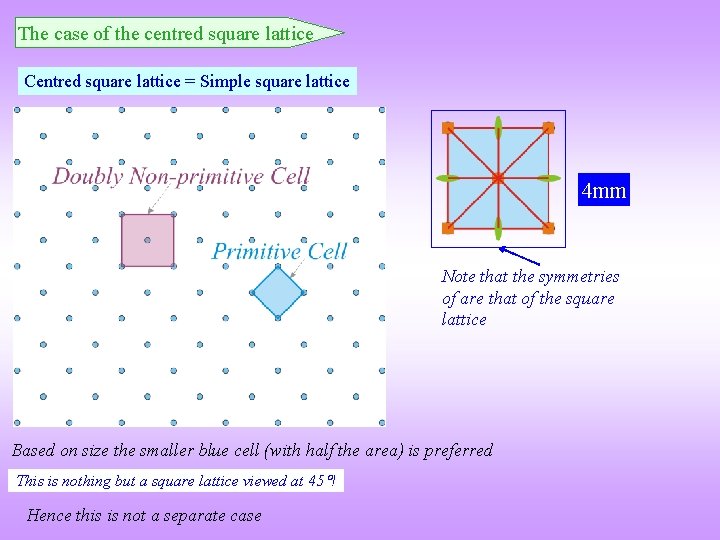
The case of the centred square lattice Centred square lattice = Simple square lattice 4 mm Note that the symmetries of are that of the square lattice Based on size the smaller blue cell (with half the area) is preferred This is nothing but a square lattice viewed at 45 ! Hence this is not a separate case

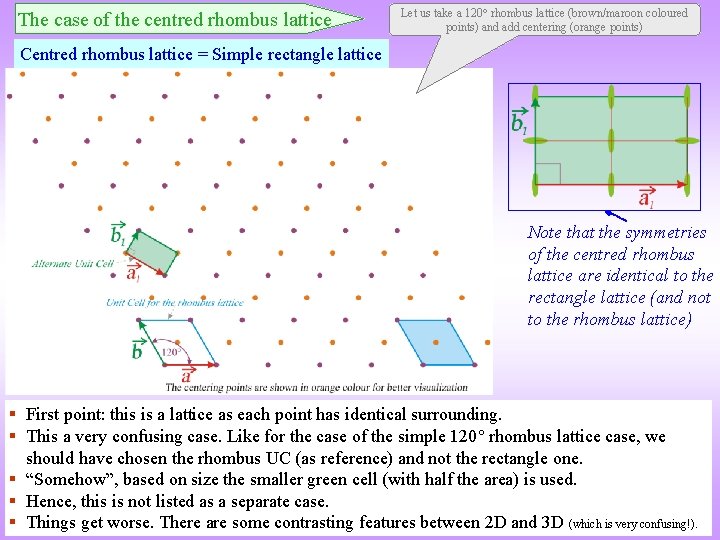
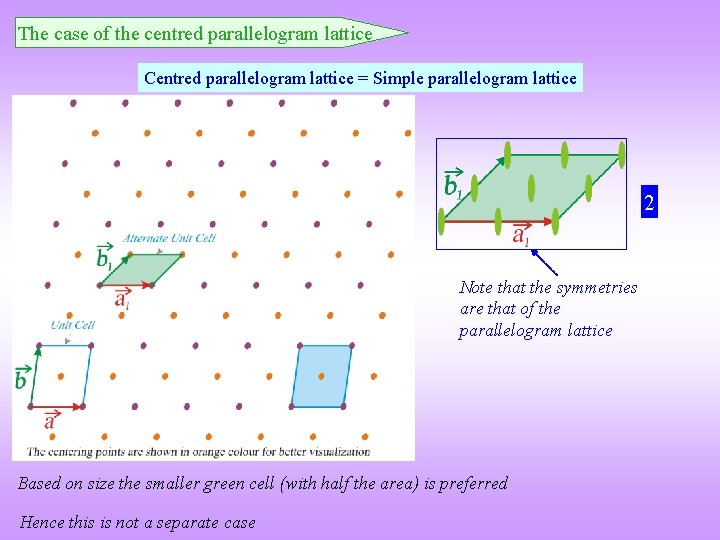
The case of the centred rhombus lattice Let us take a 120 rhombus lattice (brown/maroon coloured points) and add centering (orange points) Centred rhombus lattice = Simple rectangle lattice Note that the symmetries of the centred rhombus lattice are identical to the rectangle lattice (and not to the rhombus lattice) § First point: this is a lattice as each point has identical surrounding. § This a very confusing case. Like for the case of the simple 120 rhombus lattice case, we should have chosen the rhombus UC (as reference) and not the rectangle one. § “Somehow”, based on size the smaller green cell (with half the area) is used. § Hence, this is not listed as a separate case. § Things get worse. There are some contrasting features between 2 D and 3 D (which is very confusing!).

The case of the centred parallelogram lattice Centred parallelogram lattice = Simple parallelogram lattice 2 Note that the symmetries are that of the parallelogram lattice Based on size the smaller green cell (with half the area) is preferred Hence this is not a separate case

How can make some 2 -D crystals out of the lattices we have constructed Click here

3 D Lattices

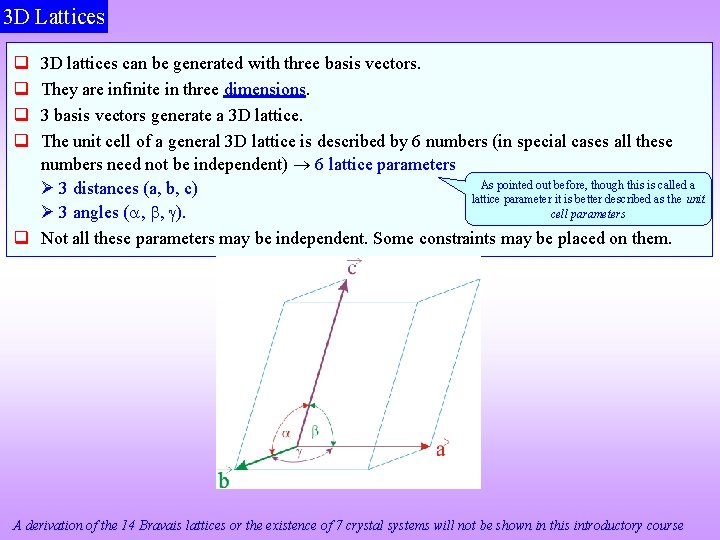
3 D Lattices 3 D lattices can be generated with three basis vectors. They are infinite in three dimensions. 3 basis vectors generate a 3 D lattice. The unit cell of a general 3 D lattice is described by 6 numbers (in special cases all these numbers need not be independent) 6 lattice parameters As pointed out before, though this is called a 3 distances (a, b, c) lattice parameter it is better described as the unit cell parameters 3 angles ( , , ). Not all these parameters may be independent. Some constraints may be placed on them. A derivation of the 14 Bravais lattices or the existence of 7 crystal systems will not be shown in this introductory course

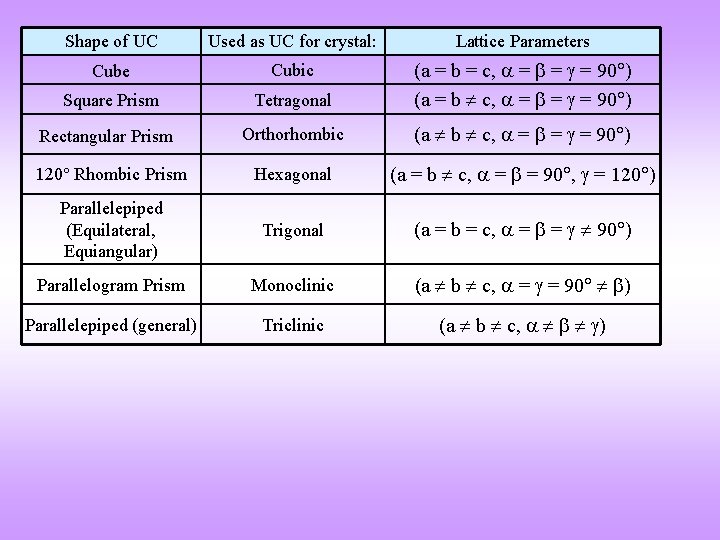
There are 14 distinct 3 D lattices which come under 7 Crystal Systems The BRAVAIS LATTICES (with shapes of unit cells as) : Cube (a = b = c, = = = 90 ) Square Prism (Tetragonal) Rectangular Prism (Orthorhombic) 120 Rhombic Prism (Hexagonal) Parallelepiped (Equilateral, Equiangular) (Trigonal) Parallelogram Prism (Monoclinic) Parallelepiped (general) (Triclinic) (a = b c, = = = 90 ) (a = b c, = = 90 , = 120 ) (a = b = c, = = 90 ) (a b c, ) To restate: the 14 Bravais lattices have 7 different Symmetries (which correspond to the 7 Crystal Systems).

Shape of UC Used as UC for crystal: Lattice Parameters Cube Cubic Square Prism Tetragonal (a = b = c, = = = 90 ) (a = b c, = = = 90 ) Rectangular Prism Orthorhombic (a b c, = = = 90 ) 120 Rhombic Prism Hexagonal (a = b c, = = 90 , = 120 ) Parallelepiped (Equilateral, Equiangular) Trigonal (a = b = c, = = 90 ) Parallelogram Prism Monoclinic (a b c, = = 90 ) Parallelepiped (general) Triclinic (a b c, )

Important Note: Do NOT confuse the shape of the unit cell with the definition of crystal systems (crystal systems are defined based on symmetry). (as we have already seen we can always choose a different unit cell for a given crystal)

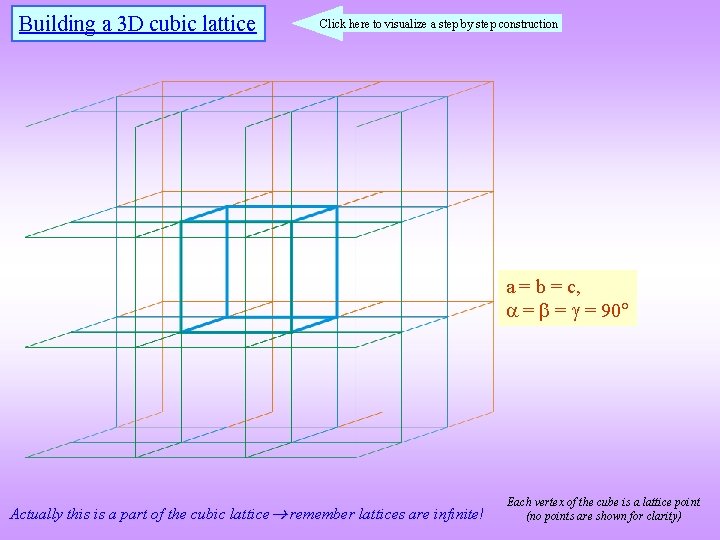
Building a 3 D cubic lattice Click here to visualize a step by step construction a = b = c, = = = 90 Actually this is a part of the cubic lattice remember lattices are infinite! Each vertex of the cube is a lattice point (no points are shown for clarity)

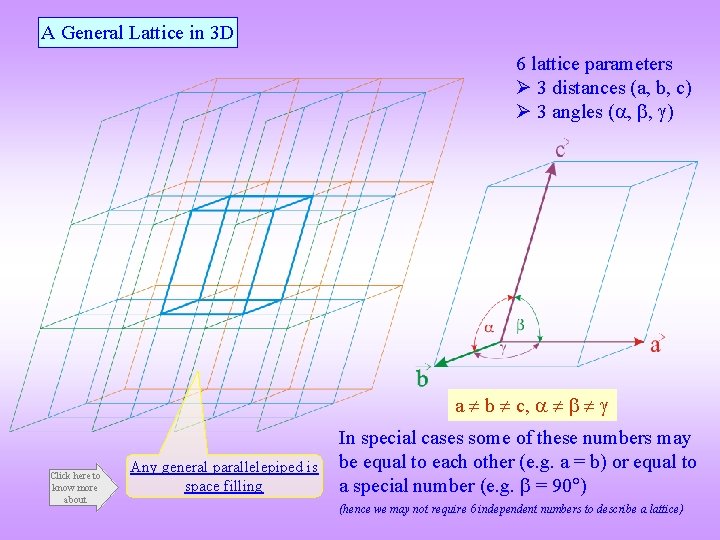
A General Lattice in 3 D 6 lattice parameters 3 distances (a, b, c) 3 angles ( , , ) a b c, Click here to know more about Any general parallelepiped is space filling In special cases some of these numbers may be equal to each other (e. g. a = b) or equal to a special number (e. g. = 90 ) (hence we may not require 6 independent numbers to describe a lattice)

Bravais Lattice: various viewpoints A lattice is a set of points constructed by translating a single point in discrete steps by a set of basis vectors. In three dimensions, there are 14 unique Bravais lattices (distinct from one another in that they have different space groups) in three dimensions. All crystalline materials recognized till now fit in one of these arrangements. In geometry and crystallography, a Bravais lattice is an infinite set of points generated by a set of discrete translation operations. A Bravais lattice looks exactly the same no matter from which point in the lattice one views it. An important property of a lattice Bravais concluded that there are only 14 possible Space Lattices (with Unit Cells to represent them). These belong to 7 Crystal systems. There are 14 Bravais Lattices which are the Space Group symmetries of lattices A derivation of the 14 Bravais lattices or the existence of 7 crystal systems will not be shown in this introductory course

Time to fasten you seat-belts the next few slides will take you on a 10 g-force dive

IMPORTANT Crystals and Crystal Systems are defined based on Symmetry & NOT Based on the Geometry of the Unit Cell Example Cubic Crystal Does NOT imply a = b = c & = = It implies the existence of two 3 -fold axis in the structure Intrigued! Want to Know More?

IMPORTANT If lattices are based on just translation (Translational Symmetry (t)) A ns w then how come other Symmetries (especially rotational) come into the picture while choosing the Ex Crystal System & Unit Cell for a lattice? am pl e Why do we say that End Centred Cubic Lattice does not exist? Isn’t it sufficient that a = b = c & = = to call something cubic? (why do we put End Centred Cubic in Simple Tetragonal? ) er The issue comes because we want to put 14 Bravais lattices into 7 boxes (the 7 Crystal Systems; the Bravais lattices have 7 distinct symmetries) and further assign Unit Cells to them The Crystal Systems are defined based on Symmetries (Rotational, Mirror, Inversion etc. forming the Point Groups) and NOT on the geometry of the Unit Cell The Choice of Unit Cell is based on Symmetry & Size (& Convention) (in practice the choice of unit cell is left to us! but what we call the crystal is not!!) Continued…

ONCE MORE: When we say End Centred Cubic End Centred is a type of Lattice (based on translation) & Cubic is a type of Crystal (based on other symmetries) & Cubic also refers to a shape of Unit Cell (based on lattice parameters) AND: To confuse things further Cubic crystals can have lower symmetry than the cubic lattice (e. g. Cubic lattices always have 4 -fold axis while Cubic Crystals may not have 4 -fold axes) Feeling lost!? ! hang on! some up-coming examples will make things CRYSTAL clear

To emphasize: The word Cubic (e. g. in a cubic crystal) refers to 3 things A type of Lattice (based on translation) & A type of Crystal (based on other symmetries) & A shape of Unit Cell (based on lattice parameters) Hence the confusion!!

Another IMPORTANT point Lattices have the highest symmetry (Which is allowed for it) Crystals based on the lattice can have lower symmetry Click here to know more

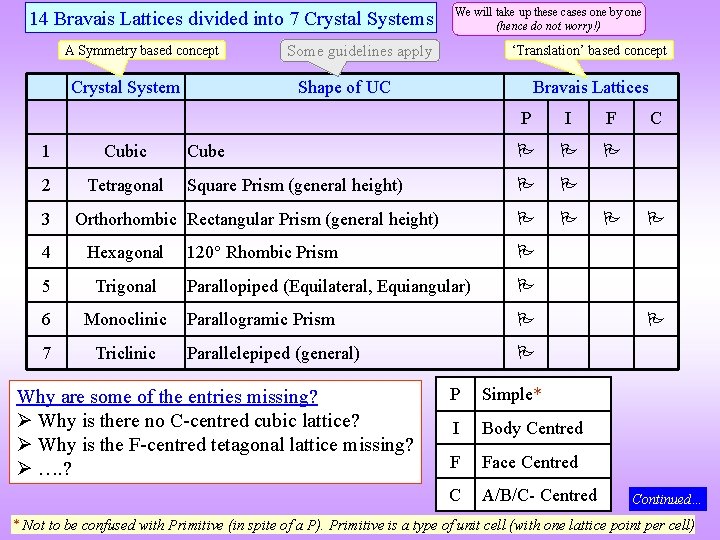
14 Bravais Lattices divided into 7 Crystal Systems A Symmetry based concept Crystal System 1 Cubic 2 Tetragonal 3 We will take up these cases one by one (hence do not worry!) ‘Translation’ based concept Some guidelines apply Shape of UC Bravais Lattices P I F Cube Square Prism (general height) Orthorhombic Rectangular Prism (general height) 4 Hexagonal 5 Trigonal 6 Monoclinic 7 Triclinic 120 Rhombic Prism Parallopiped (Equilateral, Equiangular) Parallogramic Prism Parallelepiped (general) Why are some of the entries missing? Why is there no C-centred cubic lattice? Why is the F-centred tetagonal lattice missing? …. ? P Simple* I Body Centred F Face Centred C A/B/C- Centred C Continued… * Not to be confused with Primitive (in spite of a P). Primitive is a type of unit cell (with one lattice point per cell)

Arrangement of lattice points in the Unit Cell & No. of Lattice points / Cell Position of lattice points Effective number of Lattice points / cell P 8 Corners = [8 (1/8)] = 1 I 8 Corners + 1 body centre = [1 (for corners)] + [1 (BC)] = 2 3 F 8 Corners + 6 face centres = [1 (for corners)] + [6 (1/2)] =1+3=4 4 A/ B/ C 8 corners + 2 centres of opposite faces = [1 (for corners)] + [2 (1/2)] = 2 1 2

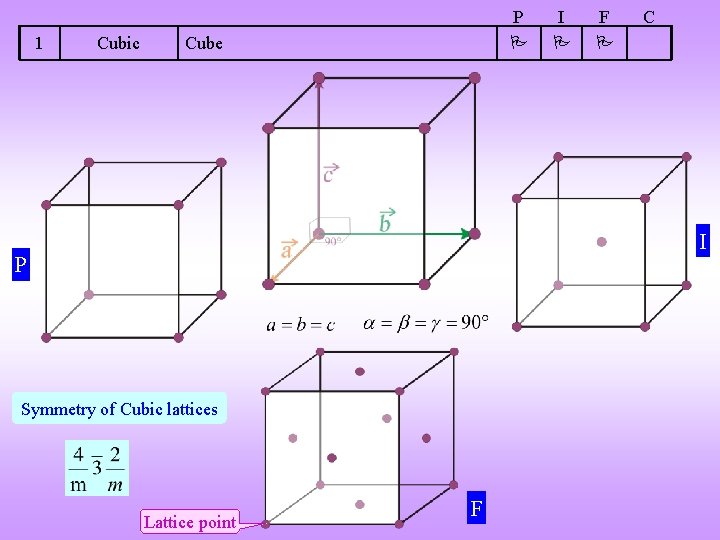
1 Cubic P Cube I F C I P Symmetry of Cubic lattices Lattice point F

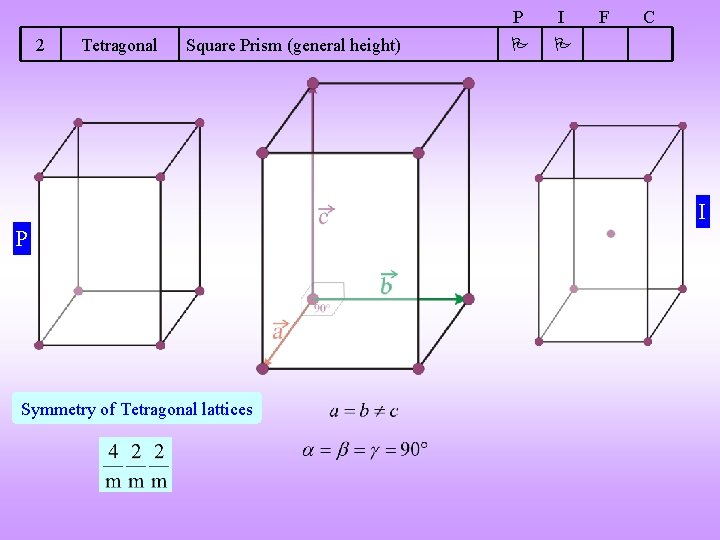
2 Tetragonal Square Prism (general height) P I F C I P Symmetry of Tetragonal lattices

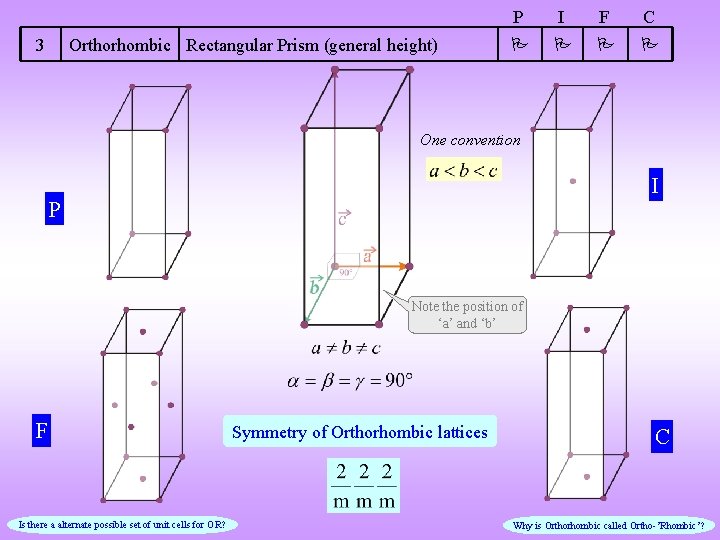
3 Orthorhombic Rectangular Prism (general height) P I F C One convention I P Note the position of ‘a’ and ‘b’ F Is there a alternate possible set of unit cells for OR? Symmetry of Orthorhombic lattices C Why is Orthorhombic called Ortho-’Rhombic’?

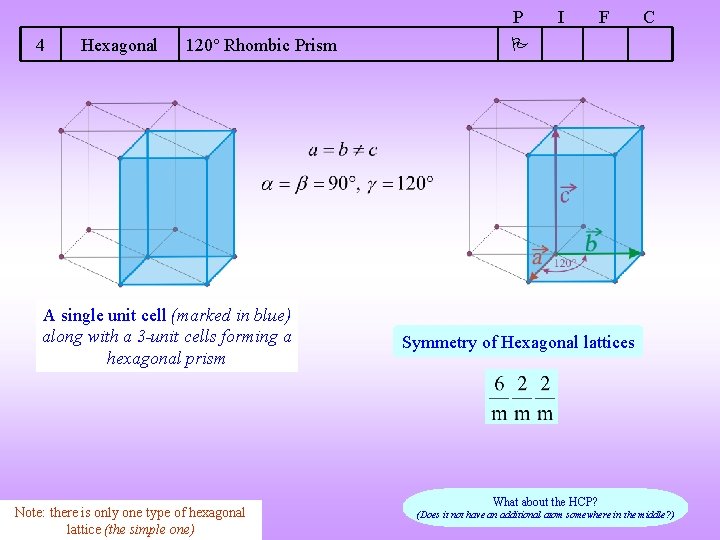
P 4 Hexagonal 120 Rhombic Prism A single unit cell (marked in blue) along with a 3 -unit cells forming a hexagonal prism Note: there is only one type of hexagonal lattice (the simple one) I F C Symmetry of Hexagonal lattices What about the HCP? (Does it not have an additional atom somewhere in the middle? )

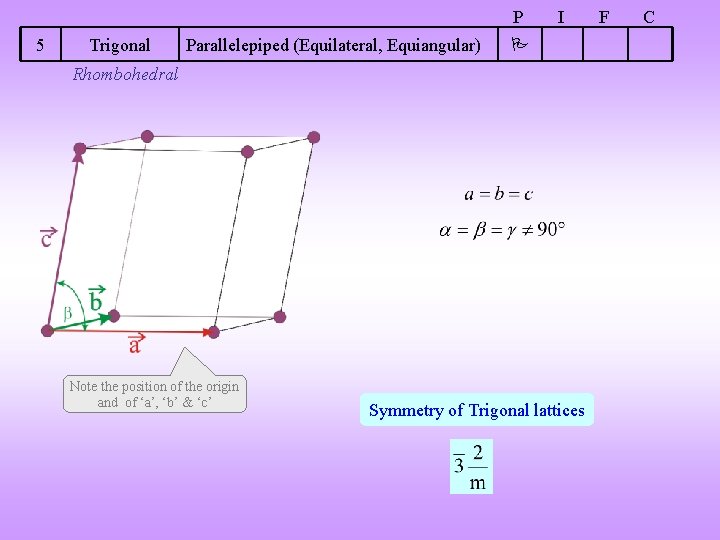
P 5 Trigonal Parallelepiped (Equilateral, Equiangular) I Rhombohedral Note the position of the origin and of ‘a’, ‘b’ & ‘c’ Symmetry of Trigonal lattices F C

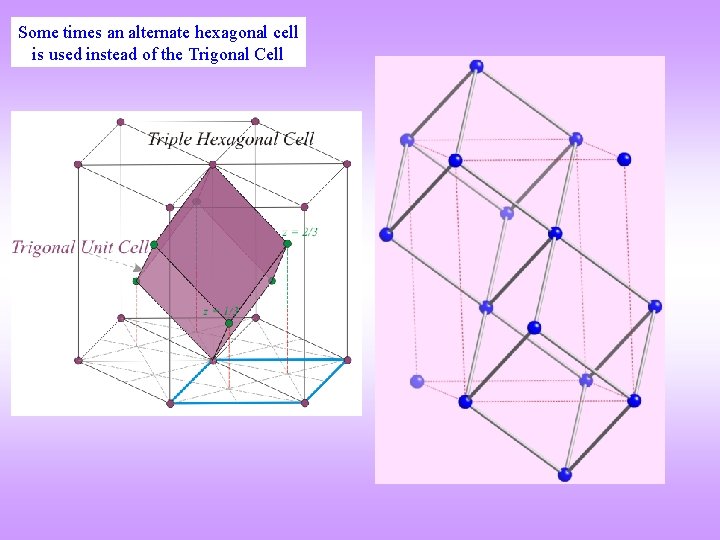
Some times an alternate hexagonal cell is used instead of the Trigonal Cell

A trigonal cell can be produced from a cubic cell by pulling along [111] (the body diagonal) (keeping the edge length of the cube constant) Video: Cubic to Trigonal UC

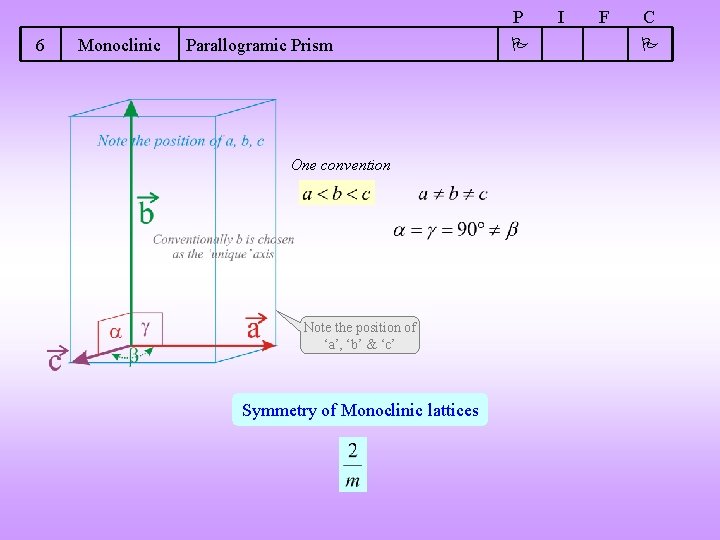
P 6 Monoclinic Parallogramic Prism One convention Note the position of ‘a’, ‘b’ & ‘c’ Symmetry of Monoclinic lattices I F C

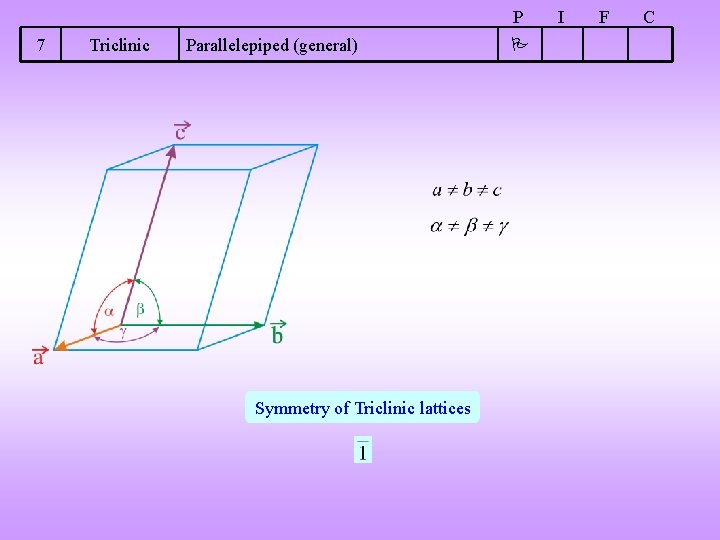
P 7 Triclinic Parallelepiped (general) Symmetry of Triclinic lattices I F C

Let us make some 3 -D crystals Click here

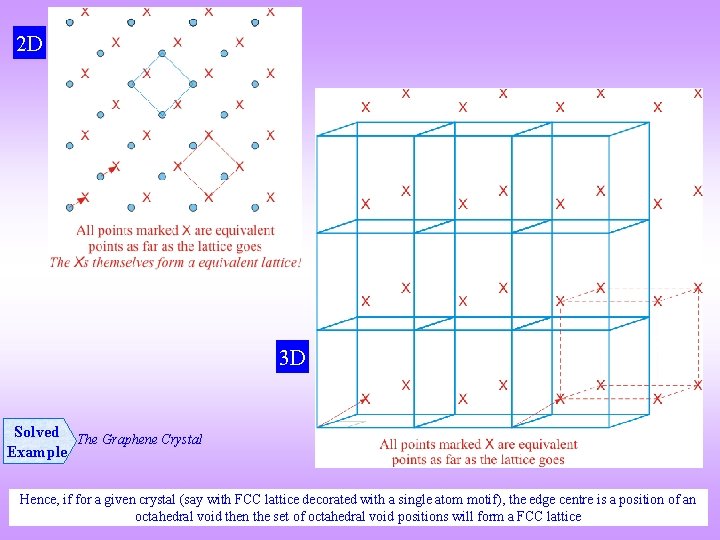
An important property of a lattices This aspect might seem trivial here but is very useful to remember! If one sits at any lattice point the space around looks identical to the person Hence we can chart out a set of equivalent points in space (Which may or may not coincide with the lattice points) 1 D The Xs themselves form an equivalent lattice

2 D 3 D Solved The Graphene Crystal Example Hence, if for a given crystal (say with FCC lattice decorated with a single atom motif), the edge centre is a position of an octahedral void then the set of octahedral void positions will form a FCC lattice

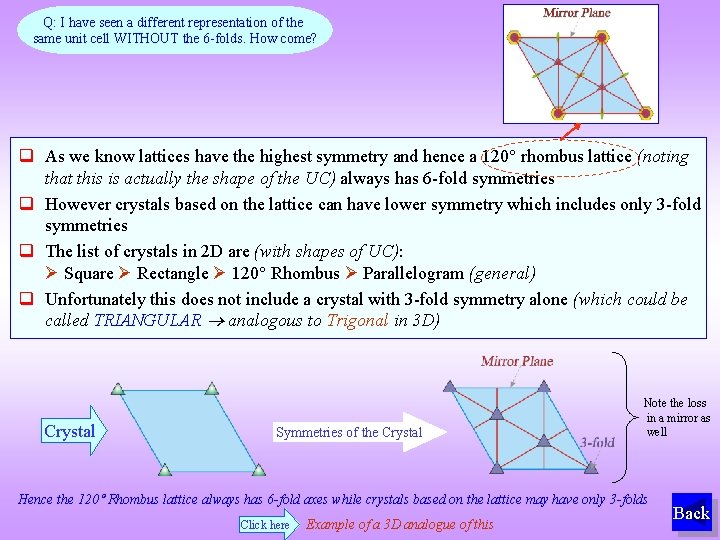
Q: I have seen a different representation of the same unit cell WITHOUT the 6 -folds. How come? As we know lattices have the highest symmetry and hence a 120 rhombus lattice (noting that this is actually the shape of the UC) always has 6 -fold symmetries However crystals based on the lattice can have lower symmetry which includes only 3 -fold symmetries The list of crystals in 2 D are (with shapes of UC): Square Rectangle 120 Rhombus Parallelogram (general) Unfortunately this does not include a crystal with 3 -fold symmetry alone (which could be called TRIANGULAR analogous to Trigonal in 3 D) Crystal Symmetries of the Crystal Note the loss in a mirror as well Hence the 120 Rhombus lattice always has 6 -fold axes while crystals based on the lattice may have only 3 -folds Click here Example of a 3 D analogue of this Back

Funda Check Is there a edge centred square lattice? No. Every point does not have identical surroundings (as shown in figure below).