Space Efficient Linear Time Construction of Suffix Arrays

Space Efficient Linear Time Construction of Suffix Arrays Pang Ko and Srinivas Aluru Dept. Electrical and Computer Engineering Laurence H. Baker Center for Bioinformatics and Biological Statistics Iowa State University Ames, Iowa 50011, USA {kopang, aluru}@iastate. edu 06/18/2003 Iowa State University

Suffix Array n n Sorted order of suffixes of a string T. Represented by the starting position of the suffix. Text M I S S I P P I Index 1 3 4 5 6 7 8 9 10 11 12 Suffix Array 12 11 8 5 2 1 10 9 7 4 2 6 $ 3 2

Brief History n n n Introduced by Manber and Myers in 1989. Takes O(n log n) time, and 8 n bytes. Many other nonlinear time algorithms. Authors Time Space (bytes) Manber & Myers n log n 8 n Sadakane n log n 9 n String-sorting n 2 log n 5 n Radix-sorting n 2 5 n 3

Our Result 1. 2. 3. 4. Among the first linear-time direct suffix array construction algorithms. Solves an important open problem. For constant size alphabet, only uses 8 n bytes. Easily implementable. Can also be used as a space efficient suffix tree construction algorithm. 4

Notation n n String T = t 1…tn. Over the alphabet Σ = {1…n}. tn = ‘$’, ‘$’ is a unique character. Ti = ti…tn, denotes the i-th suffix of T. For strings and , < denotes is lexicographically smaller than . 5

Overview n Divide all suffixes of T into two types. n n n Type S suffixes = {Ti | Ti < Ti+1} Type L suffixes = {Tj | Tj > Tj+1} The last suffix is both type S and L. Sort all suffixes of one of the types. Obtain lexicographical order of all suffixes from the sorted ones. 6

Identify Suffix Types Type L S L Text M I L S L S S I M > II < SS=>S, I ÞT 1 > ÞT 2 so Þ <check TT 33> Tnext 4 > T 5 character ÞT 1 is Þtype T 2 Þ is TLtype S T 4 are type L 3 and L L P P I L/S $ The type of each suffix in T can be determined in one scan of the string. 7

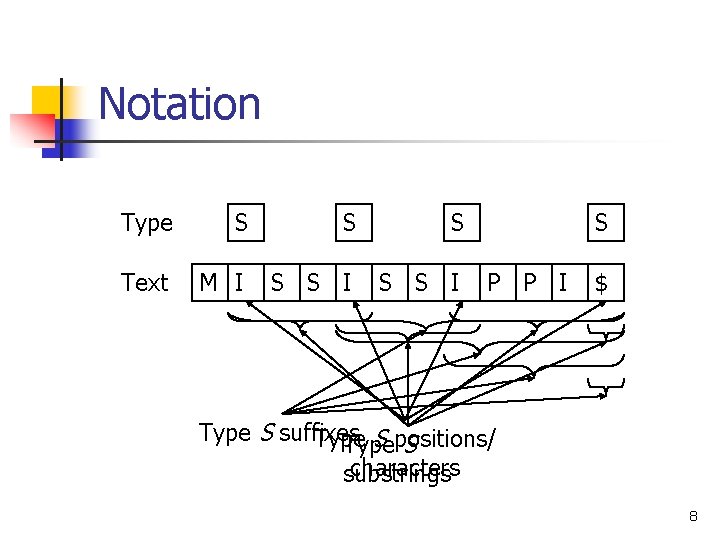
Notation Type S S S Text M I S S I S P P I $ Type S suffixes Type S positions/ Type S characters substrings 8

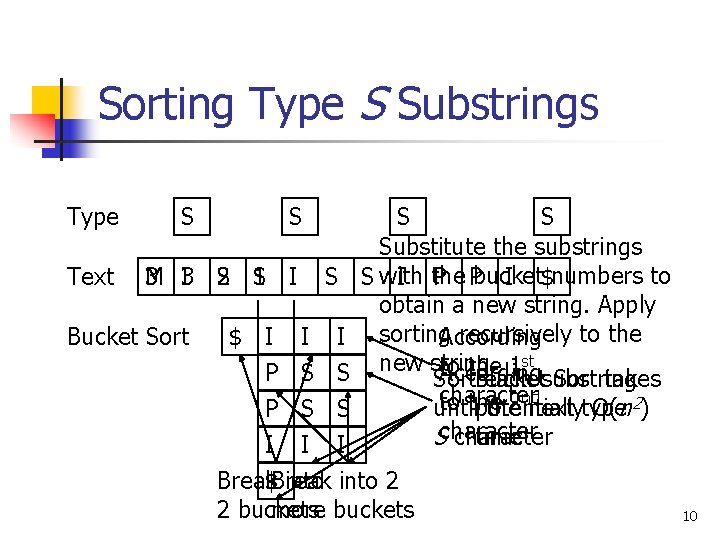
Sorting Type S Suffixes n n Sort all type S substrings. Replace each type S substrings by its bucket number. New string is the sequence of bucket numbers. Sorting all type S suffixes = Sorting all suffixes of the new string. 9

Sorting Type S Substrings Type Text S S M 3 3 I 2 S 1 S I Bucket Sort S Substitute the substrings S with I the P Pbucket I $numbers to obtain a new string. Apply sorting recursively to the According st new string. to the 1 According Sort Bucket each substring Sort takes nd character to the 2 untilpotentially the next type O(n 2) Scharacter time $ I I I P S S I I I Break$Break into 2 2 buckets more buckets 10

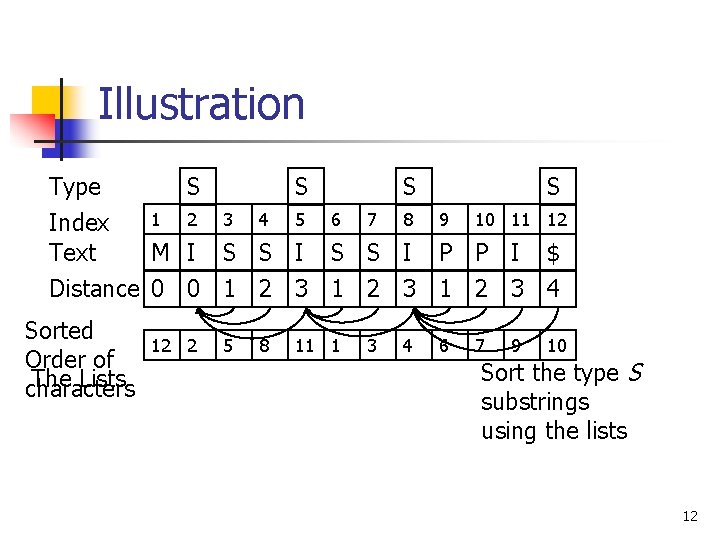
Solution n Observation: Each character participates in the bucket sort at most twice. n n Type L characters only participate in the bucket sort once. Solution: n n Sort all the characters once. Construct m lists according the distance to the closest type S character to the left 11

Illustration Type S S 1 2 3 4 5 6 7 8 9 10 11 12 Index Text M I S S I P P I $ Distance 0 0 1 2 3 4 Sorted Order of The Lists characters 12 2 5 8 11 1 3 4 6 7 9 10 Sort the type S substrings using the lists 12

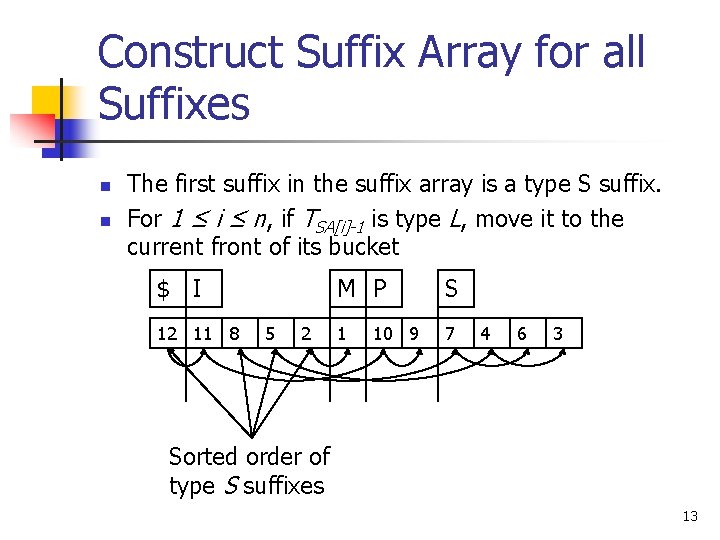
Construct Suffix Array for all Suffixes n n The first suffix in the suffix array is a type S suffix. For 1 ≤ i ≤ n, if TSA[i]-1 is type L, move it to the current front of its bucket $ I 12 11 8 5 2 M P S 1 7 10 9 4 6 3 Sorted order of type S suffixes 13

Run-Time Analysis n n Identify types of suffixes -- O(n) time. Bucket sort type S (or L) substrings -O(n) time. Construct suffix array from sorted type S (or L) suffixes -- O(n) time. T(n) = T(n/2) + O(n) = O(n) 14

Space Requirement n n For each element in an array use 2 integers to mark the beginning and the end of their bucket. Use Boolean array to mark the boundary of each bucket. This takes 12 n bytes for |Σ|~n. At most 3 n bits is needed for the Boolean arrays. 15

Constant size Alphabet n n n No need to create the m lists. Because bucket sort takes O(n) time. Reducing the space needed to 4 n bytes for the 1 st recursion step. Maximum space used at anytime is 8 n bytes (and maximum of 3 Boolean arrays). 16

Suffix Trees n n Most suffix tree construction algorithms take O(n|Σ|) time. (Ukkonen, Weiner, Mc. Creight) Farach’s algorithm takes O(n) time for large integer alphabet. n n n Hard to implement. Uses a lot of space. Our algorithm can be used to build the suffix array then convert it into the suffix tree. (By using linear time LCP computation algorithm by Kasai et. al. ) 17

Conclusion n n Among the first suffix array construction algorithm takes O(n) time. The algorithm can be easily implemented in 8 n bytes (plus a few Boolean arrays). Equal or less space than most non-linear time algorithm. Can be used as a space efficient suffix tree construction algorithm. 18