Space Complexity Reminder P NP classes P NP

Space Complexity

Reminder: P, NP classes • P • NP is the class of problems for which: – Guessing phase: A polynomial time algorithm generates a plausible solution S – Checking phase: A polynomial time algorithm certifies that if S is correct • A problem npc is NP-complete if: – npc is in NP – For every other problem np in NP, there is a polynomial time algorithm that transforms np into npc (polynomial reduction)

P is a subset of NP • If a problem p is in P, there is an algorithm A solving p and A runs in polynomial time • How do we show that it is in NP? Ø Make A the generation phase ØConstruct an algorithm that always returns “true” as the checking phase: check(P, S) return true

A new Problem • WIN: Generate a winning strategy for a 2 -person, turnbased, perfect information, deterministic game. Example? –For example: Chess –Winning strategy: “policy” on Ju. Ke. CB • Suppose that the game is finite. Example? – Chess, we assume that if it reaches 100 moves then the game ends with a tide • The “n” for making complexity analysis is: The number of moves made during a game

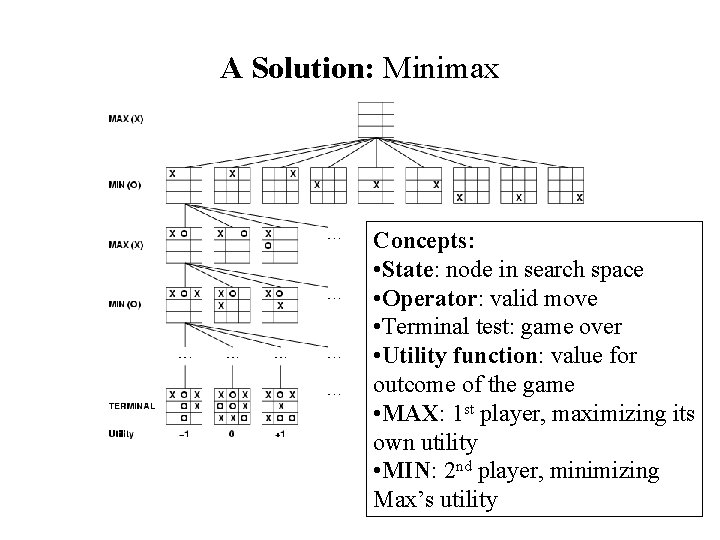
A Solution: Minimax Concepts: • State: node in search space • Operator: valid move • Terminal test: game over • Utility function: value for outcome of the game • MAX: 1 st player, maximizing its own utility • MIN: 2 nd player, minimizing Max’s utility

Let us examine the complexity • Is minimax polynomial? No. This requires exploring exponential many branches • Can we show that it is in NP? (think certification phase) No. The minimax tree itself is exponential. So certifying it by using the minimax tree will require exponential time • So is WIN not in NP? We do not know. Likely it is not in NP ØNo one has been able to proof that is in NP (or P) ØNo one has been able to proof that it is not in NP (or P)

PSPACE • PSPACE is the class of all problems that can be solved with algorithms that use a polynomial amount of memory (regardless of the time they take to run) • Examples: ØSAT. §((x y) ¬x) y §We systematically try every combination: q 0010, 0111, 1000, 1101 q 2 n possible combinations q But only O(n) space used Ø Same trick is use to show that NP is a subset of PSPACE: q. Systematically generate each potential solution (need polynomial space only to keep track) q. Check if it is a solution

PSPACE-complete • A problem psc is PSPACE-complete if: Øpsc is in PSPACE ØFor every other problem ps in PSPACE, there is a polynomial time algorithm that transforms ps into psc (polynomial reduction) • Example: ØQBF: Satisfaction of quantified Boolean formulas: x y((x y) ¬x) y

QBF: Quantified Boolean Formulas • Qx 1 Qx 2 Qx 3 …Qxn f(x 1, x 2, …, xn) • Where – Each xi is a variable – f(x 1, x 2, …, xn) is a Boolean formula without quantifiers – x 1, x 2, …, xn are the only variables in f – Qxi can be either xi or xi • (QSAT) Decision problem: Given a QBF, is it true? false? • Observation 1: Seems difficult to prove that QSAT is in NP • Observation 2: It is easy to prove that QSAT is in PSPACE

Transforming WIN into QSAT (Example illustrating QSAT PSPACE-completeness) • QBF Formula for indicating if a winning formula exists: – Suppose x 1, x 2, x 3, … xn are variables for 1 st, 2 nd, 3 rd, . . moves by Player 1 – Suppose y 1, y 2, y 3, … yn are variables for 1 st, 2 nd, 3 rd, . . moves by Player 2 – Suppose that win. Player 1(x 1, y 1, x 2, y 2, …, yn) indicates that Player 1 wins when the game sequence is x 1, y 1, x 2, y 2, …, yn – Under this circumstances a winning strategy for Player 1 can be represented as the QBF Formula: x 1 y 1 x 2 y 2 … yn win(x 1, y 1, …, yn)

EXP-Classes • EXPTIME is the class of problems that can be solved with algorithms that runs in exponential time – Usual definition for EXPTIME-complete – Example: Go • EXPSPACE is the class of all problems that can be solved with algorithms that use an exponential amount of memory – Usual definition for ESPSPACE-complete – Example: HTN Planning with “regularity” • We know: P NP PSPACE EXPTIME EXPSPACE