Space complexity AB 4 InputWorkOutput TM Input Tape

Space complexity [AB 4]

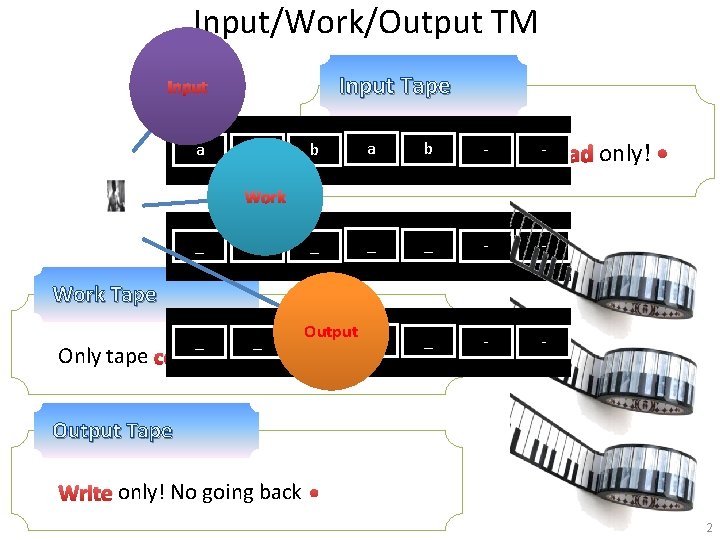
Input/Work/Output TM Input Tape Input a a b - -Read only! _ _ _ - - Output _ _ _ - - • Work _ _ Work Tape Only tape counted • Output Tape Write only! No going back • 2

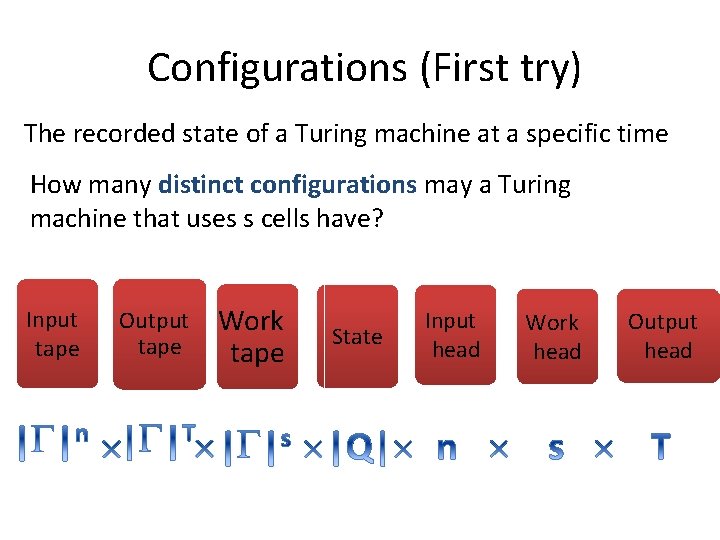
Configurations (First try) The recorded state of a Turing machine at a specific time How many distinct configurations may a Turing machine that uses s cells have? Input tape Output tape Work tape State Input head Work head Output head

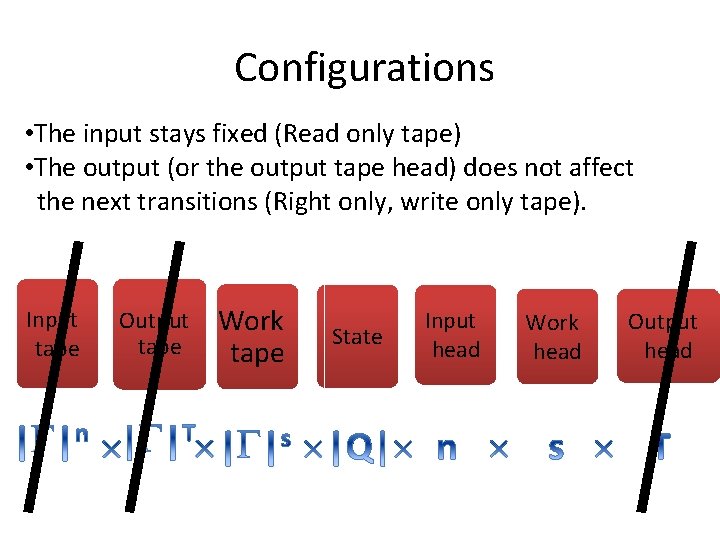
Configurations • The input stays fixed (Read only tape) • The output (or the output tape head) does not affect the next transitions (Right only, write only tape). Input tape Output tape Work tape State Input head Work head Output head

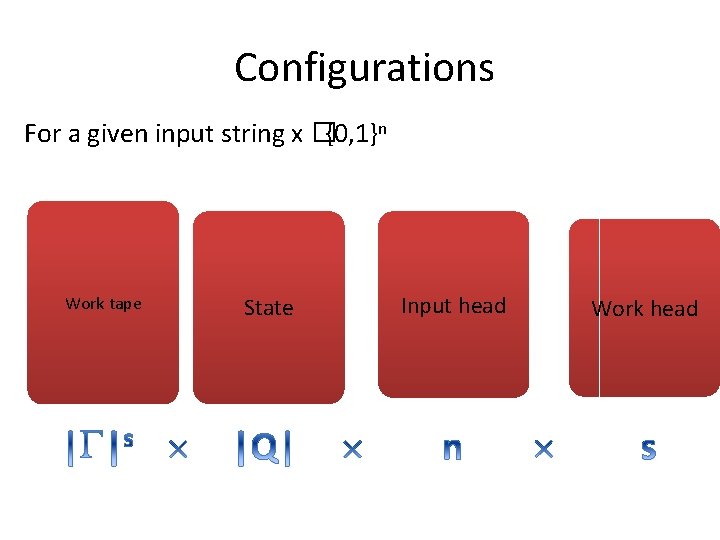
Configurations For a given input string x �{0, 1}n Work tape State Input head Work head

Space complexity Def: The space complexity of a Turing Machine T on input x is the maximal number of tape cells used throughout the computation.

Definition: Space-Complexity • Let t: N N be a complexity function Deterministic space: Det. Log space: PS PA C E L Det polynomial space: 7

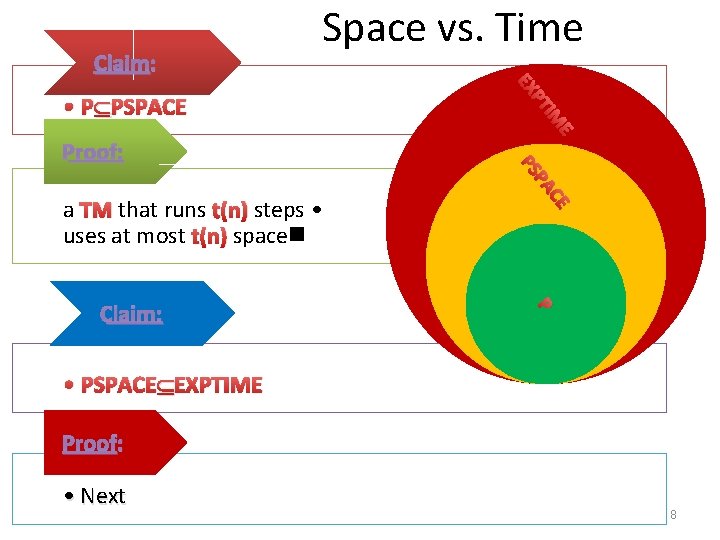
Claim: Space vs. Time CE PA P Claim: E TIM a TM that runs t(n) steps • uses at most t(n) space PS Proof: P EX • P PSPACE • PSPACE EXPTIME Proof: • Next 8

The Configuration graph for a given input x. Gx=(V, E) V – All possible configurations for the given input x. E – An edge between configurations c and c’, if there exists a legal �step from c to c’.

PSPACE �EXP Proof: A deterministic run that halts must avoid repeating a configuration its running time is bounded from above by the number of configurations the machine has, which, for a PSPACE machine, is at most exponential

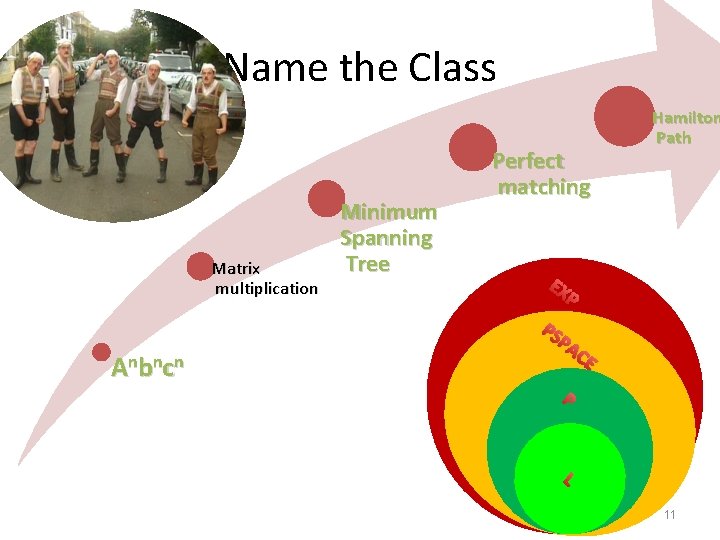
Name the Class Matrix multiplication A nb ncn Minimum Spanning Tree Perfect matching Hamilton Path EX P PS PA CE P L 11