Sound wave longitudinal wave of compressions and rarefactions

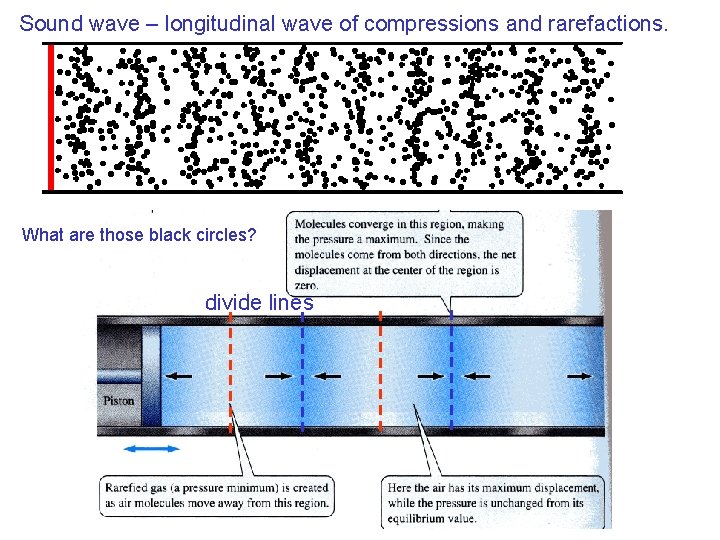
Sound wave – longitudinal wave of compressions and rarefactions. What are those black circles? divide lines

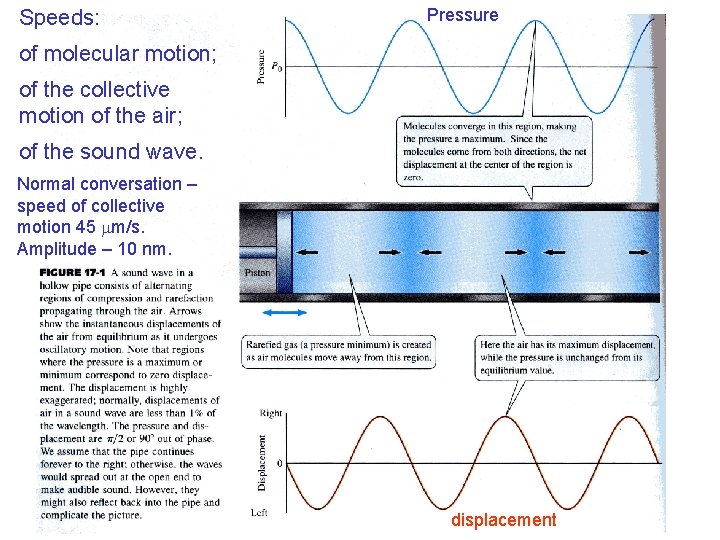
Speeds: Pressure of molecular motion; of the collective motion of the air; of the sound wave. Normal conversation – speed of collective motion 45 mm/s. Amplitude – 10 nm. displacement

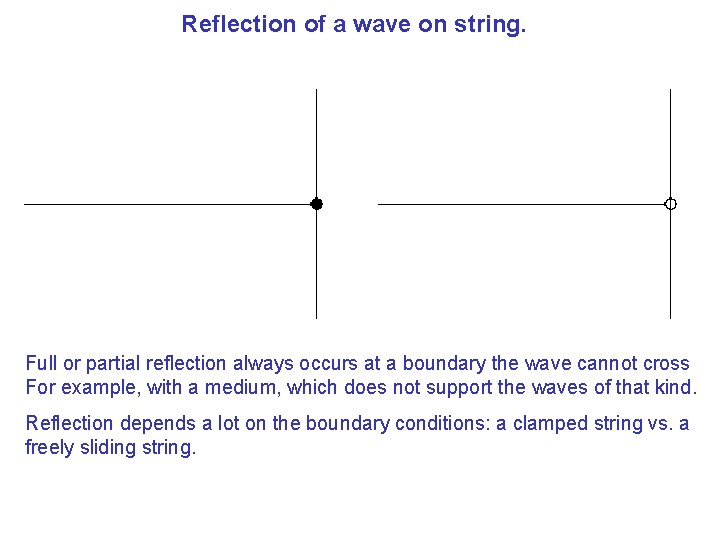
Reflection of a wave on string. Full or partial reflection always occurs at a boundary the wave cannot cross For example, with a medium, which does not support the waves of that kind. Reflection depends a lot on the boundary conditions: a clamped string vs. a freely sliding string.

Reflection of a wave on string. A partial reflection always occurs if properties of the medium change abruptly. Abruptly compared to what? Examples: reflection of sound off a rock, light off a glass window… Two connected strings. What is different between them, F ? M ? How do the wave speed in them compare? What about the amplitudes?

Refraction of waver waves… Refraction – change in the direction of wave propagation at a boundary. Waves change direction, or refract, as they enter shallow water, because the waves slow down.

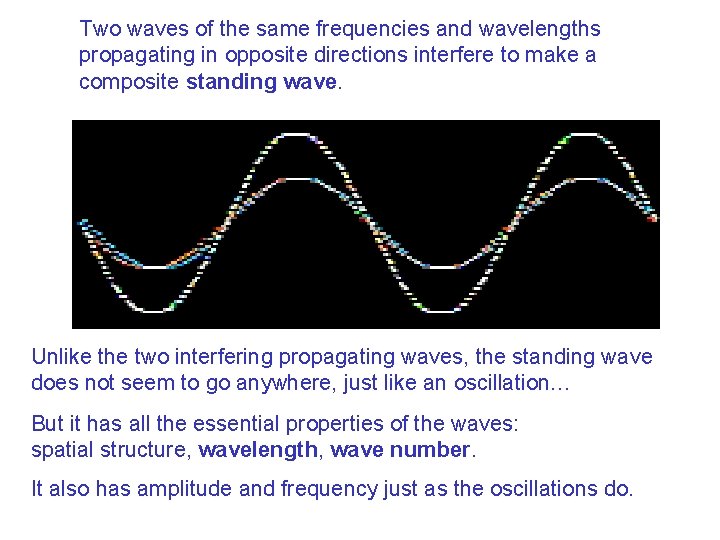
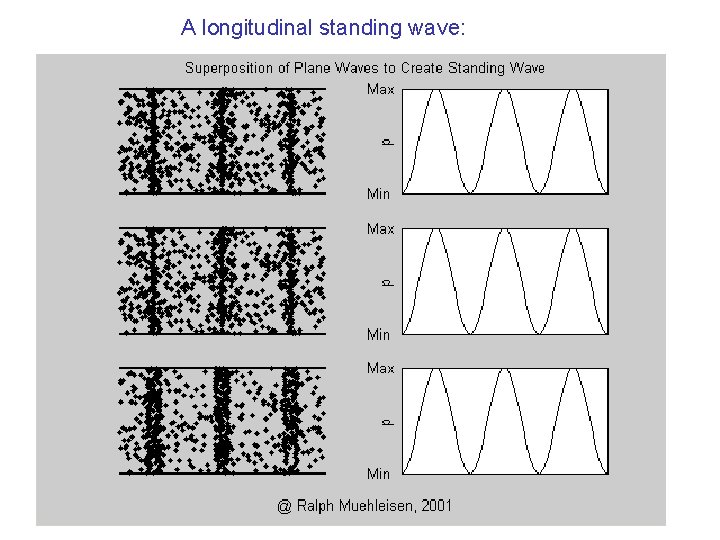
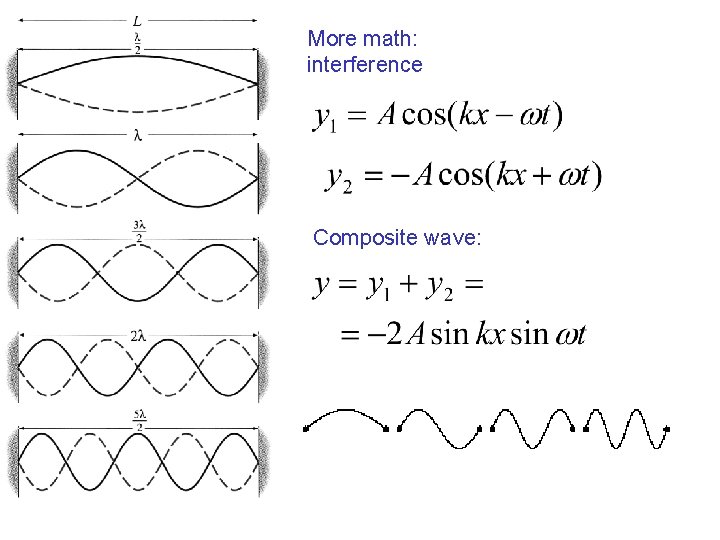
Two waves of the same frequencies and wavelengths propagating in opposite directions interfere to make a composite standing wave. Unlike the two interfering propagating waves, the standing wave does not seem to go anywhere, just like an oscillation… But it has all the essential properties of the waves: spatial structure, wavelength, wave number. It also has amplitude and frequency just as the oscillations do.

A longitudinal standing wave:

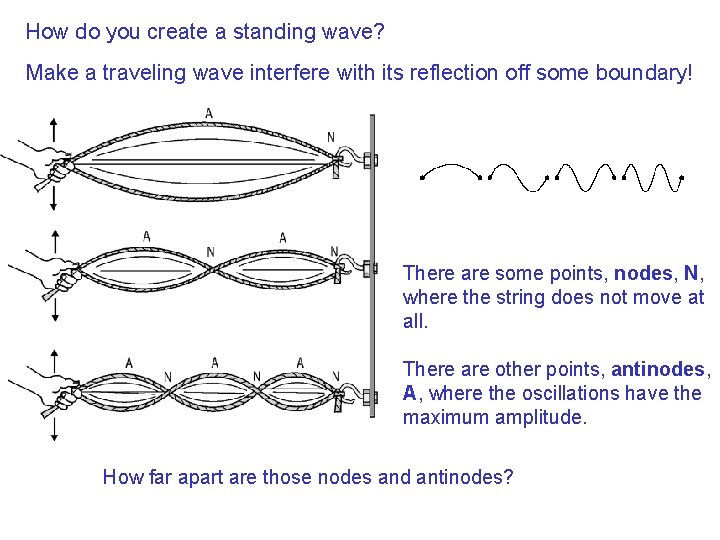
How do you create a standing wave? Make a traveling wave interfere with its reflection off some boundary! There are some points, nodes, N, where the string does not move at all. There are other points, antinodes, A, where the oscillations have the maximum amplitude. How far apart are those nodes and antinodes?

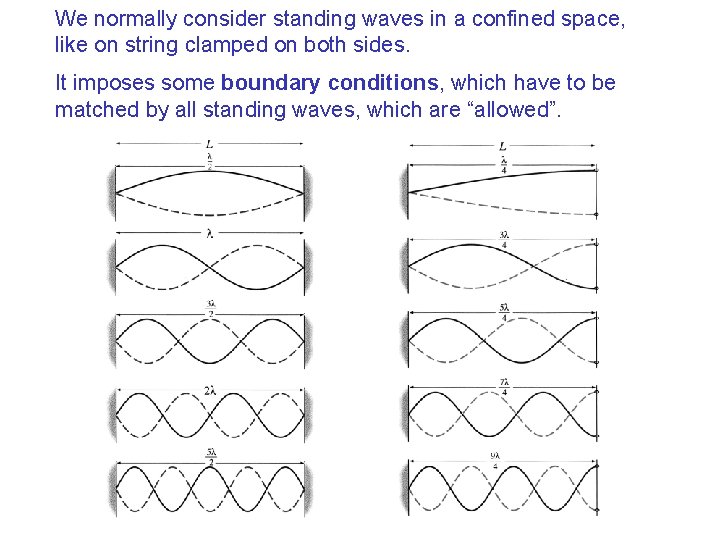
We normally consider standing waves in a confined space, like on string clamped on both sides. It imposes some boundary conditions, which have to be matched by all standing waves, which are “allowed”.

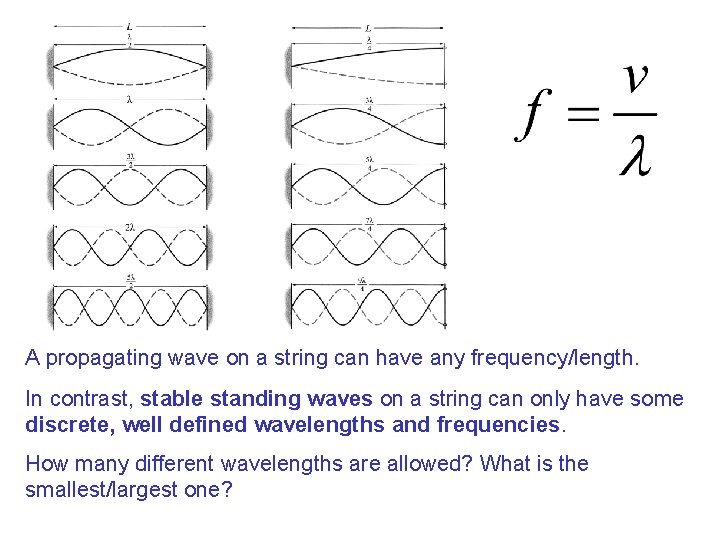
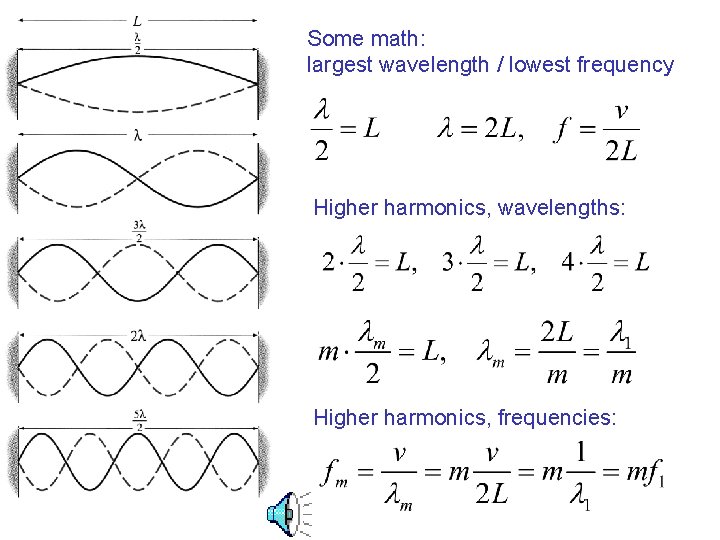
A propagating wave on a string can have any frequency/length. In contrast, stable standing waves on a string can only have some discrete, well defined wavelengths and frequencies. How many different wavelengths are allowed? What is the smallest/largest one?

Some math: largest wavelength / lowest frequency Higher harmonics, wavelengths: Higher harmonics, frequencies:

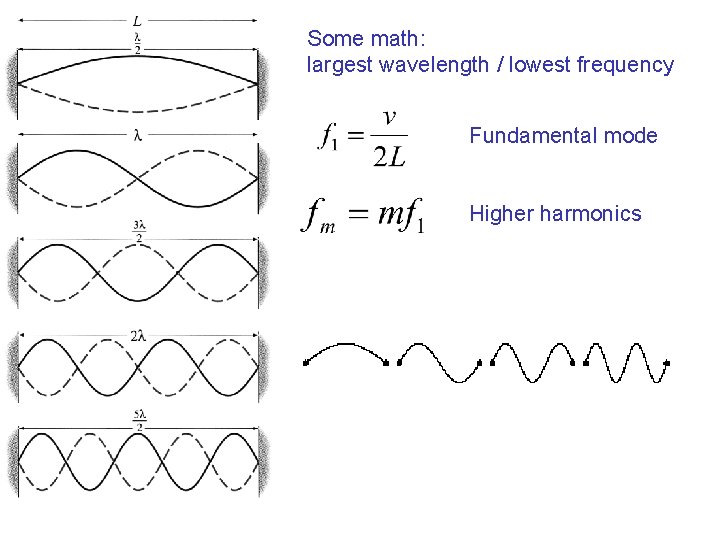
Some math: largest wavelength / lowest frequency Fundamental mode Higher harmonics

More math: interference Composite wave:

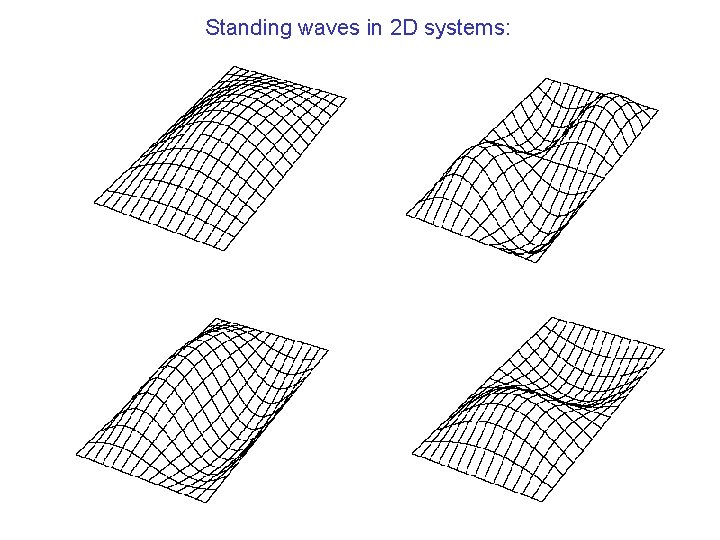
Standing waves in 2 D systems:

Resonance - a vibration of large amplitude in a mechanical or electrical system caused by a relatively small periodic stimulus of the same or nearly the same period as the natural vibration period of the system. Requires: a system capable to vibrate with a reasonable small damping; an external driving force with a frequency close to that of the system. http: //www. youtube. com/w atch? v=YLBt_07 -Vek

Question: why are we discussing resonance now and have not discussed it while talking about propagating waves? Propagating waves do not have any special natural wavelengths and frequencies. Both wavelengths and frequencies can vary continuously. Standing waves have a particular set of allowed frequencies, which are characteristic for the system. Fundamental mode Higher harmonics