Sound Production of sound Sound waves are longitudinal

Sound

Production of sound • Sound waves are longitudinal – Air molecules vibrate in SHM producing compressed areas (high density) and expanded or rarefacted areas (low density) • Crest – high density • Trough – low density

Characteristics • Frequencies that the human ear can respond to are called “audible”. – Range from 20 to 20 000 Hz • Infrasonic – frequencies below 20 Hz • Ultrasonic – frequencies above 20 000 Hz The “pitch” of a sound is determined by its frequency.

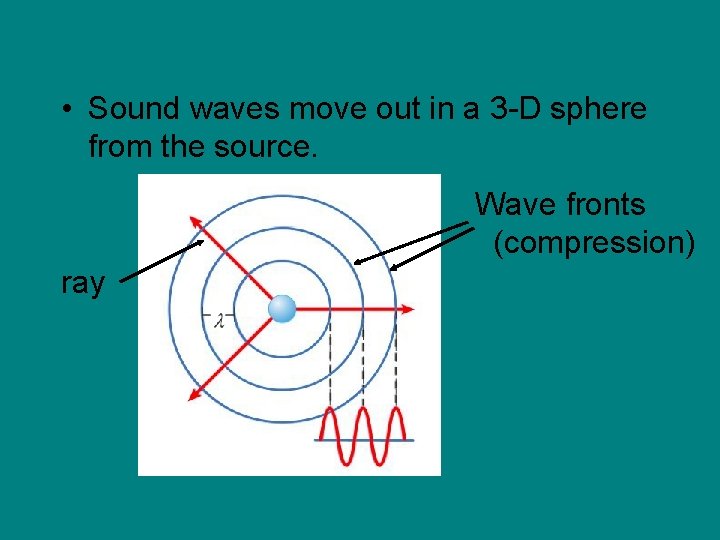
• Sound waves move out in a 3 -D sphere from the source. Wave fronts (compression) ray

• The speed of a sound wave depends on the medium through which it moves. The frequency is set by the source of the sound. If the speed changes due to a change in medium it is the wavelength (λ) that will change.

Speed of Sound • The speed of sound depends on the medium. – As density of the medium increases, speed increases. – As temperature of the medium increases, speed increases • And will decrease as the temp decreases • The speed at 0 o. C is 331 m/s for dry air pre. AP -- the speed of sound changes by 0. 6 m/s for each degree from 0 o C

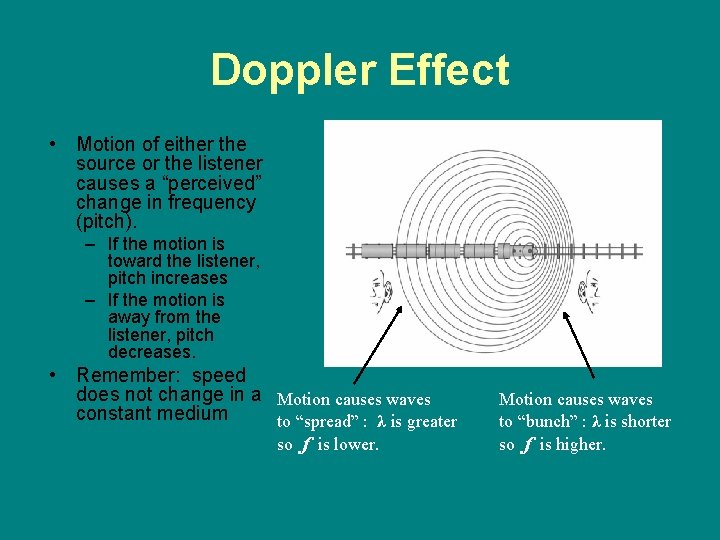
Doppler Effect • Motion of either the source or the listener causes a “perceived” change in frequency (pitch). – If the motion is toward the listener, pitch increases – If the motion is away from the listener, pitch decreases. • Remember: speed does not change in a Motion causes waves constant medium to “spread” : λ is greater so f is lower. Motion causes waves to “bunch” : λ is shorter so f is higher.

pre. AP only - Doppler Calculation • • • v = velocity of sound in air vs = velocity of source vo = velocity of observer or detector f = frequency of source (emitted freq) f ' = apparent frequency (detected freq)) Upper signs = moving toward Lower signs = away

A truck’s horn blows at a frequency of 500 Hz. A boy on a bicycle moves toward the truck at 10 m/s. What is the apparent frequency heard by the boy? Assume sound travels at 340 m/s. f ’ = 500 Hz (340 m/s + 10 m/s) (340 m/s – 0 m/s) f ’ = 500 Hz ( 350/340) = 515 Hz Notice = the objects are moving toward each other so the wave fronts are “bunched” together and the pitch (perceived frequency) goes up.

Sound Intensity Sound intensity is the power of a sound wave per unit area. • Sound waves move out in a 3 -D sphere from the source so area is 4 pr 2. • Intensity is an inverse square relationship. • I = intensity (W/m 2) • P = Power of source (watts) • r = distance from source (m)

pre. AP only - Relative Intensity a ratio of the sound intensity to threshold of hearing I = intensity (W/m 2) Io = 10 -12 W/m 2 (threshold of hearing) = decibels (d. B)

Comparison of Sound Intensities The inverse square relationship means a sound that is twice as far away is one-fourth as intense, and one that is three times as far away is oneninth as intense. Comparing intensity of a sound at two distances: The comparison reduces to the intensities and the radii since the power is constant (from the same source) and 4π is also constant.

A horn blows with constant power. A child 8 m away hears a sound of intensity 0. 600 W/m 2. What is the intensity heard by his mother 20 m away? What is the power of the source? Given: I 1 = 0. 60 W/m 2; r 1 = 8 m, I 1 r 12 = I 2 r 22 I 2 = 0. 096 W/m 2 r 2 = 20 m

From the previous example: What is the power of the source? Given: I 1 = 0. 60 W/m 2; r 1 = 8 m I 2 = 0. 0960 W/m 2 ; r 2 = 20 m P = 7. 54 W

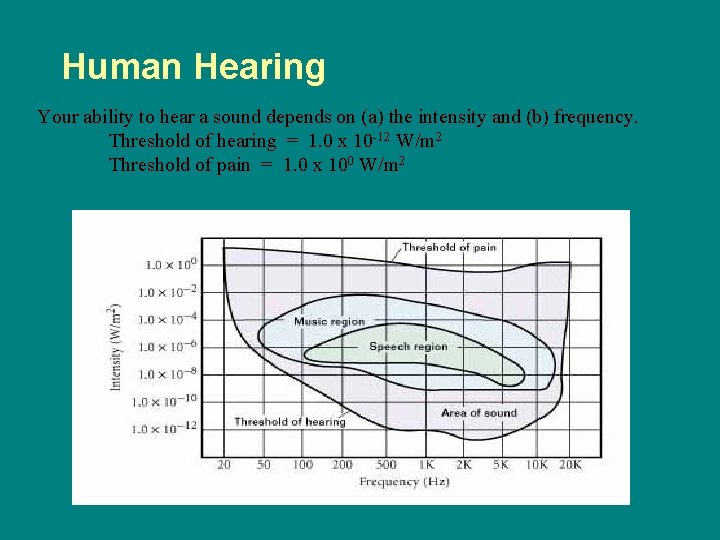
Human Hearing Your ability to hear a sound depends on (a) the intensity and (b) frequency. Threshold of hearing = 1. 0 x 10 -12 W/m 2 Threshold of pain = 1. 0 x 100 W/m 2

Relative Intensity • When a sound is given a “decibel” rating, the intensity of that sound is being compared to the threshold of hearing.

Concepts (log scale) • A 10 d. B increase = 10 times the intensity – 10 x the pressure on your ear • A 10 d. B increase = twice the loudness – double the volume to your hearing Example: One sound is at 40 d. B and the other at 60 d. B. This is a difference of 20 or 2 x 10. The intensity is 102 greater (100 x) and the loudness is 2 x greater (twice as loud).

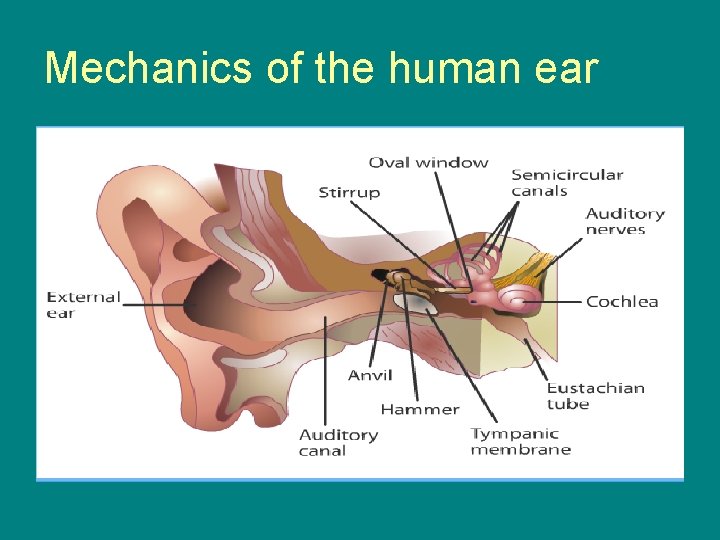
Mechanics of the human ear

Comparing your perception of the sound with the physical measurements Sensory effects Physical property Loudness Intensity Pitch Frequency Quality Waveform

Remember units! • • • Frequency -- Hertz (cycles/sec) Period -- seconds Wavelength -- meters Wave speed -- m/s Sound Intensity -- W/m 2 Relative sound intensity -decibels (d. B)

Resonance • Every system has a natural frequency at which it will oscillate. • If a force causes vibration at that frequency, the object will respond by vibrating. This is called resonance or resonance matching

Standing waves on strings • • When a string of a set length vibrates at its lowest frequency (fundamental) a standing wave is produced with nodes at each end. As the frequency increases, more waveforms are produced 1 st harmonic or fundamental frequency: L = (1/2) What frequency will produce this wave? f 1 = (v/2 L) 2 nd harmonic (1 st overtone): L =(2/2) f 2 = 2(v/2 L) or 2 (f 1) 3 rd harmonic (2 nd overtone): L = (3/2) f 3 = 3(v/2 L) or 3 ( f 1)

Resonance and Fundamental Frequency in air columns (tubes) • Open ends have an antinode • Closed or fixed ends have a node • fundamental frequency is lowest frequency possible (called the 1 st harmonic) • use length of pipe (or string) to calculate wavelength or vice versa • use speed of sound = 343 m/s, if not given

Resonance in Open Pipes General equation for frequency: fn = n(v/2 L) n = all integers Note: open pipes have the same frequency pattern as strings. The lowest frequency is ½ of a full wave but with antinodes at each open end. Stringed instruments act as fixed ends with nodes at each end.

Resonance in closed-end pipes 1 st harmonic or fundamental frequency: L = (1/4) What frequency will produce this wave? f 1 = (v/4 L) • 3 rd harmonic (1 st overtone): L =(3/4) f 3 = 3(v/4 L) or 3 x f 1 • 5 th harmonic (2 nd overtone): L = (5/4) f 5 = 5(v/4 L) or 5 x f 1 General equation for frequency: fn n = odd integers = n(v/4 L)

Beats • Beats occur due to interference patterns between sound waves of slightly different frequencies. Hear alternating loud and soft sounds. • Sounds with frequencies separated by 7 Hertz or less will produce beats that can be detected by the human ear.