Sound Production of sound Sound waves are longitudinal

Sound

Production of sound • Sound waves are longitudinal – Air molecules vibrate in SHM producing compressed areas (high density) and expanded or rarefacted areas (low density) • Crest – high density • Trough – low density

Characteristics • Frequencies that the human ear can respond to are called “audible”. – Range from 20 to 20 000 Hz • Infrasonic – frequencies below 20 Hz • Ultrasonic – frequencies above 20 000 Hz The “pitch” of a sound is determined by its frequency.

• The speed of a sound wave depends on the medium through which it moves. The frequency is set by the source of the sound. If the speed changes due to a change in medium it is the wavelength (λ) that will change.

Speed of Sound: • The speed of sound depends only on the properties of the medium it’s travelling through. • In general, sound travels fastest through solids. This is because molecules in a solid medium are much closer together than those in a liquid or gas. • The speed of sound through a gas depends on the temperature. – Speed increases as temperature increases.

Sound Intensity Sound intensity is the power of a sound wave per unit area. • Sound waves move out in a 3 -D sphere from the source so area is 4 pr 2. • Intensity is an inverse square relationship. • I = intensity (W/m 2) • P = Power of source (watts) • r = distance from source (m)

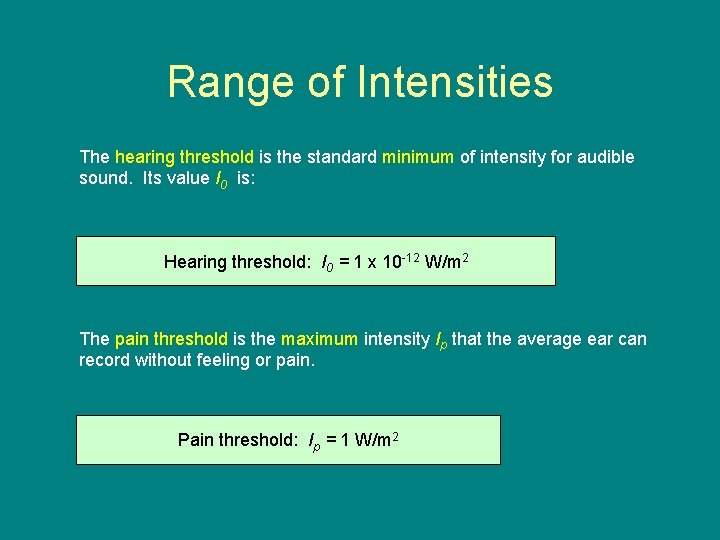
Range of Intensities The hearing threshold is the standard minimum of intensity for audible sound. Its value I 0 is: Hearing threshold: I 0 = 1 x 10 -12 W/m 2 The pain threshold is the maximum intensity Ip that the average ear can record without feeling or pain. Pain threshold: Ip = 1 W/m 2

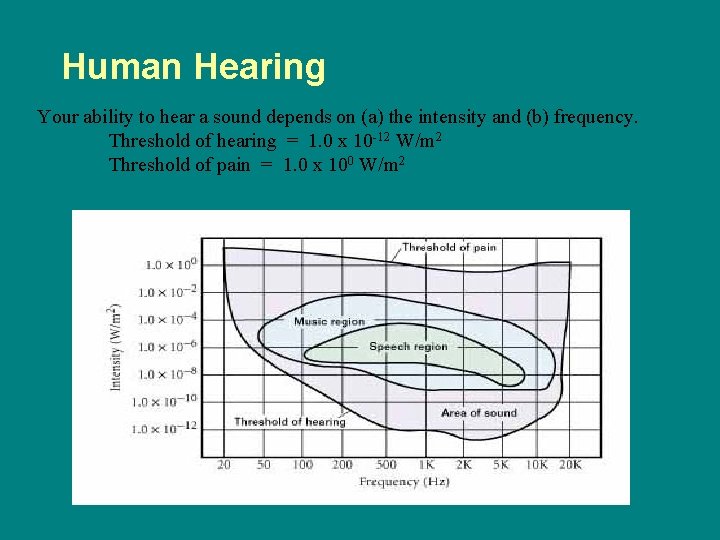
Human Hearing Your ability to hear a sound depends on (a) the intensity and (b) frequency. Threshold of hearing = 1. 0 x 10 -12 W/m 2 Threshold of pain = 1. 0 x 100 W/m 2

Relative Intensity • When a sound is given a “decibel” rating, the intensity of that sound is being compared to the threshold of hearing.

Concepts (log scale) • A 10 d. B increase = 10 times the intensity – 10 x the pressure on your ear • A 10 d. B increase = twice the loudness – double the volume to your hearing Example: One sound is at 40 d. B and the other at 60 d. B. This is a difference of 20 or 2 x 10. The intensity is 102 greater (100 x) and the loudness is 2 x greater (twice as loud).

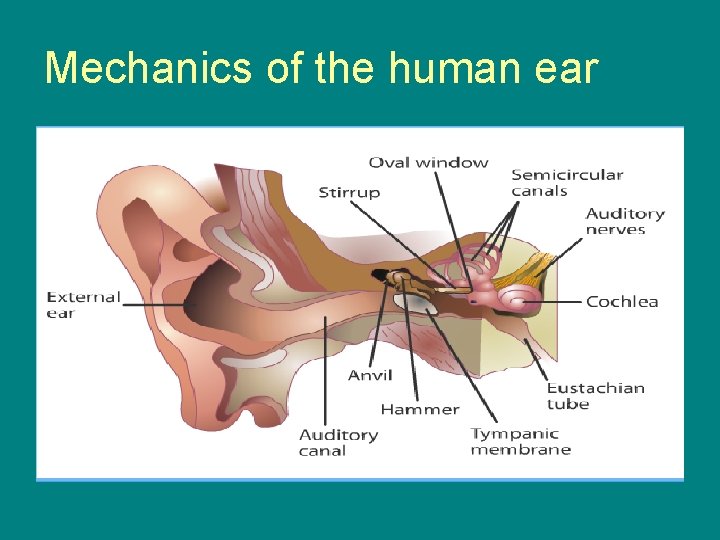
Mechanics of the human ear

Comparing your perception of the sound with the physical measurements Sensory effects Physical property Loudness Intensity Pitch Frequency Quality Waveform

Remember units! • • • Frequency -- Hertz (cycles/sec) Period -- seconds Wavelength -- meters Wave speed -- m/s Sound Intensity -- W/m 2 Relative sound intensity -decibels (d. B)

Resonance • Every system has a natural frequency at which it will oscillate. • If a force causes vibration at that frequency, the object will respond by vibrating. This is called resonance or resonance matching

Standing Waves and Harmonics

Standing Waves on a string (like a guitar) A guitar string is held in tension at each end. When it is plucked there is a wave on the string. This is called a standing wave. It is produced by interference (constructive and destructive) happening on the string. What about wind instruments? For wind instruments what is vibrating is not a string but the air inside the instrument. A note is produced when the air vibrates in a “standing wave”. This is interference in the pressure wave produced when the sound is made.

Here is a photo of a standing wave on a guitar string. It is the string at the far right – notice how the string is vibrating sideways.

Standing waves on strings • When a standing wave is produced, at the ends of the string there is no movement – points of no movement are called nodes. – These nodes are created by complete destructive interference • The place with the greatest movement is called an antinode. – These antinodes are caused by complete constructive interference.

Here is a picture of a physics demo producing a standing wave on a string that has two antinodes and three nodes. Antinodes Nodes

When a wave vibrates at a faster rate (a higher frequency) then more and more antinodes are produced. We count the antinodes to determine the number of waves produced. (It takes two antinodes to form one complete wavelength. ) When the string vibrates at its slowest rate (lowest frequency) only one antinode is produced. This is called the “fundamental frequency” (also called the First harmonic)

Standing waves on strings • • The fundamental frequency is the lowest frequency value. As the string vibrates faster, only certain frequencies will produce these wave patterns. These are called the “harmonic” frequencies. 1 st harmonic or fundamental frequency One antinode 2 nd harmonic (1 st overtone): Two antinodes 3 rd harmonic (2 nd overtone): Three antinodes

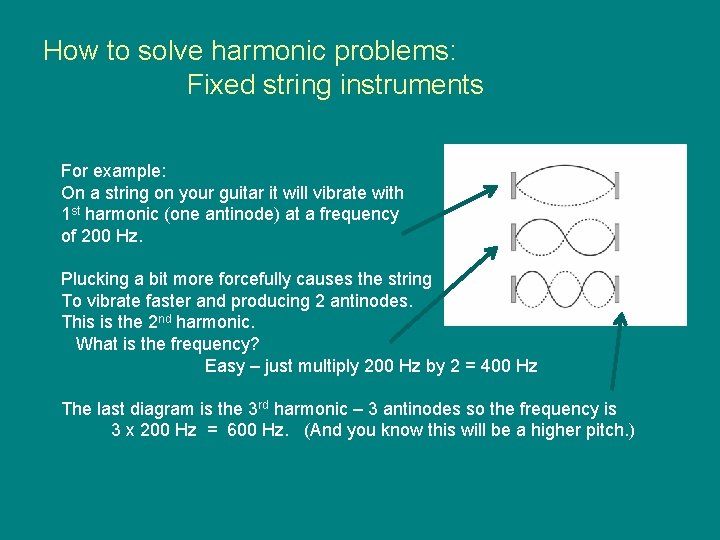
How to solve harmonic problems: Fixed string instruments For example: On a string on your guitar it will vibrate with 1 st harmonic (one antinode) at a frequency of 200 Hz. Plucking a bit more forcefully causes the string To vibrate faster and producing 2 antinodes. This is the 2 nd harmonic. What is the frequency? Easy – just multiply 200 Hz by 2 = 400 Hz The last diagram is the 3 rd harmonic – 3 antinodes so the frequency is 3 x 200 Hz = 600 Hz. (And you know this will be a higher pitch. )

Standing “pressure” waves in air (wind instruments) • There are two types: open end and closed end – Open end: like a flute • Has the same pattern as a string instrument • Produces all possible harmonics – Closed end: like a clarinet or trumpet • Produces only the odd harmonics

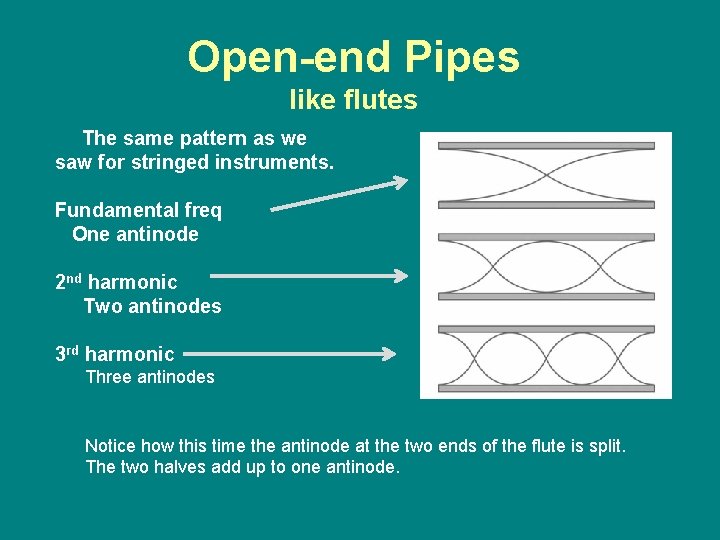
Open-end Pipes like flutes The same pattern as we saw for stringed instruments. Fundamental freq One antinode 2 nd harmonic Two antinodes 3 rd harmonic Three antinodes Notice how this time the antinode at the two ends of the flute is split. The two halves add up to one antinode.

Harmonics for open pipes • Same pattern as string instruments • The fundamental frequency (1 st harmonic) is the lowest pitch. • Each harmonic level (2 nd, 3 rd, 4 th, etc) is a multiple of the fundamental. • All harmonics are produced.

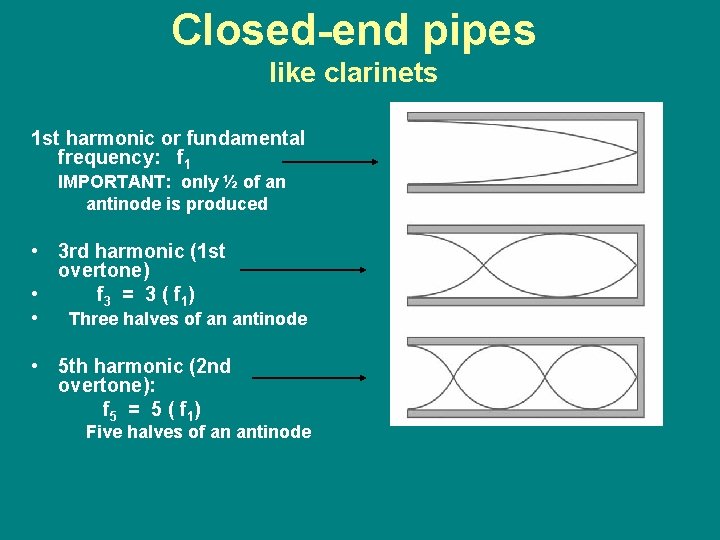
Closed-end pipes like clarinets 1 st harmonic or fundamental frequency: f 1 IMPORTANT: only ½ of an antinode is produced • 3 rd harmonic (1 st overtone) • f 3 = 3 ( f 1) • Three halves of an antinode • 5 th harmonic (2 nd overtone): f 5 = 5 ( f 1 ) Five halves of an antinode

Harmonics for closed pipes (closed only at one end) • A node forms at the closed end • An antinode forms at the open end – Only ½ of the antinode is produced • Count “½ antinodes” for this pattern – Only the odd harmonics are produced – 3 rd, 5 th, 7 th, etc. – Even harmonics are NOT formed

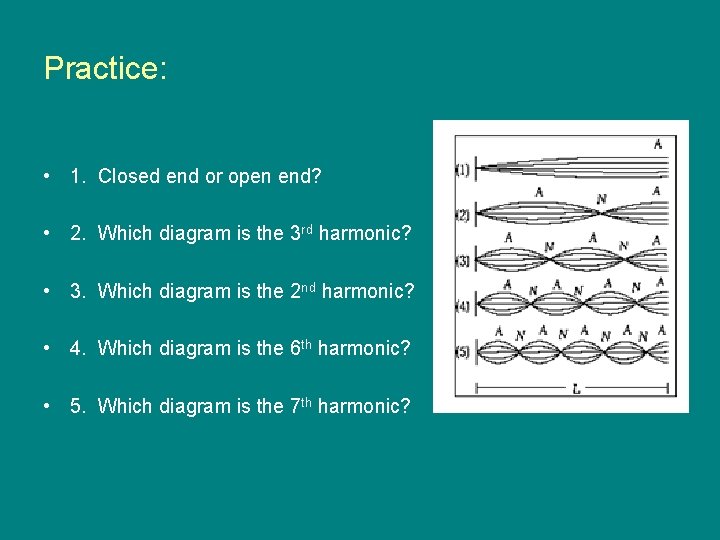
Practice: • 1. Closed end or open end? • 2. Which diagram is the 3 rd harmonic? • 3. Which diagram is the 2 nd harmonic? • 4. Which diagram is the 6 th harmonic? • 5. Which diagram is the 7 th harmonic?

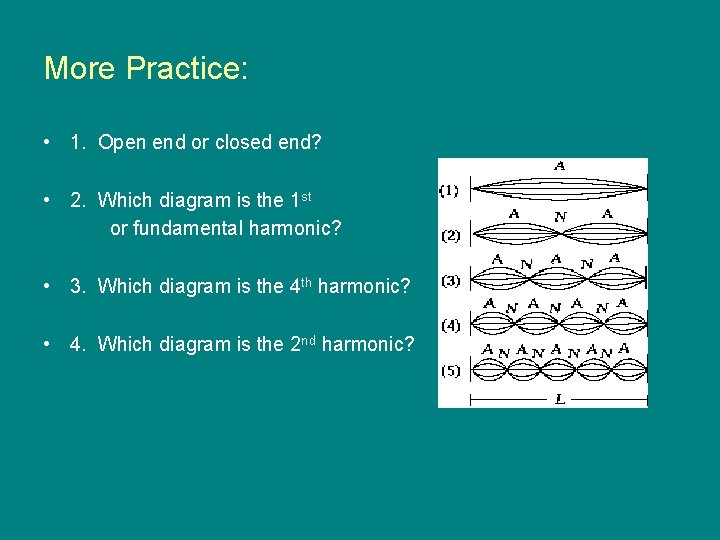
More Practice: • 1. Open end or closed end? • 2. Which diagram is the 1 st or fundamental harmonic? • 3. Which diagram is the 4 th harmonic? • 4. Which diagram is the 2 nd harmonic?

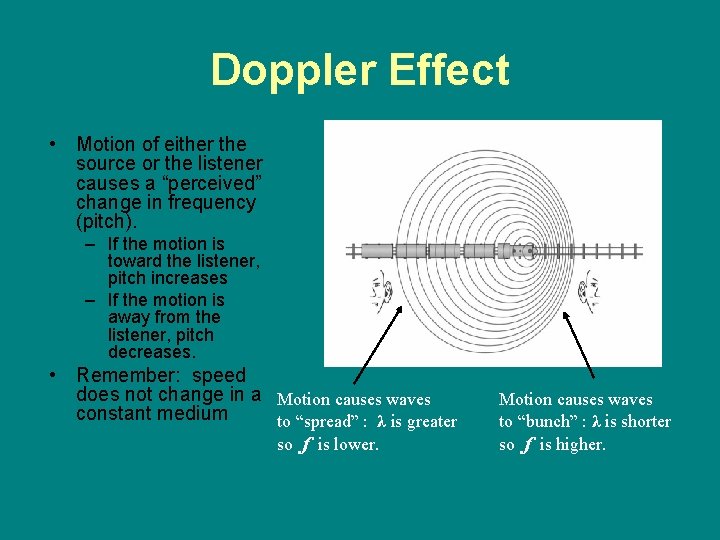
Doppler Effect • Motion of either the source or the listener causes a “perceived” change in frequency (pitch). – If the motion is toward the listener, pitch increases – If the motion is away from the listener, pitch decreases. • Remember: speed does not change in a Motion causes waves constant medium to “spread” : λ is greater so f is lower. Motion causes waves to “bunch” : λ is shorter so f is higher.

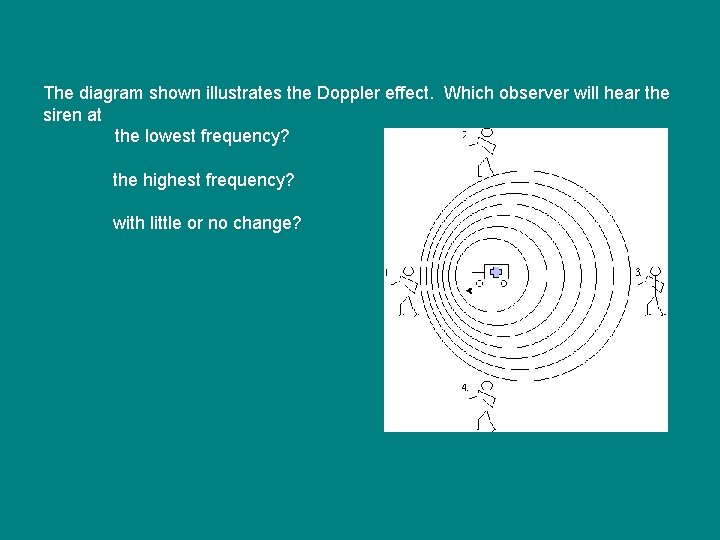
The diagram shown illustrates the Doppler effect. Which observer will hear the siren at the lowest frequency? the highest frequency? with little or no change?

Sound wave Behavior: Reflection An echo is a reflected sound wave.

Echoes: sound reflection You’re standing at the bottom of a canyon, and wondering how far away the other side is. To figure out the distance across the canyon, you could yell, and clock the time until you heard your echo. Let's say this took exactly 3. 0 seconds. Since you took physics, you know that sound travels at about 0. 2 miles per second. How far away is the other wall of the canyon? D = V x T = (0. 2 mi/sec)(1. 5 sec) D = 0. 3 miles Why was the time divided in half?

Another echo: A ship on the surface of the water sends a SONAR signal, and it bounces off a submarine in the water. If the ship is 5000 m from the sub, how long will it take for the sound engineer on the ship to hear the return echo? (The speed of sound in water is 1450 meters/sec). T = (2 x D) / V = (10 000 m) / (1450 m/s) T = 6. 9 s Why was the distance doubled?

Practice: • The speed of sound in air on a mild day is 343 m/s. A cliff is 650 m away so you clap your hand to hear the echo. How long does it take before you hear it?

More Practice: • On a really warm day sound travels at 348 m/s. If it takes 3. 2 sec to hear the echo of your voice from a far building, how far away is the building?

Sound Wave Behavior: Diffraction involves a change in direction of waves as they pass through an opening or around a barrier in their path.

Sound Wave Behavior: Diffraction Sound waves diffract better than light. The reason for the difference is that sound waves are much, much larger than light waves. The amount of diffraction increases with increasing wavelength and decreases with decreasing wavelength.