Sorting Why Sorting Sorting things is a classic

Sorting

Why Sorting? • Sorting things is a classic problem that many of us may take for granted. Understanding how sorting algorithms work and are implemented will make you a better programmer and problem solver. • Can you think of real life examples of when you use sorting? Sort clothes, sort food in fridge, sort dishes after washing,

Why Sorting? • Just how often are sorting algorithms actually discussed? • Shouldn’t this be a solved problem? • Well… • The following polls stackoverflow for sorting functions runs them until it returns the correct answer https: //gkoberger. github. io/stacksort/ • New sorting algorithms were discovered even in the early 2000 s such as Timsort and library sort

How many? • Just how many sorting algorithms can there be? Here is a small incomplete list: bubble, shell, comb, bucket, radix, insertion, selection, merge, heap, quick, Bogo, Tim, and library.

Lets sort • We will look at a few sorts and their complexities • Bubble • Insertion • Selection • Quick • Heap

Sorting Situations • Are some sorts better than others? • Yes, in some cases • There also more factors to think about than just computational complexity • overhead of initialization? • space complexity? • To see some common sorts in action with different sizes of data and conditions of the data see the animations here http: //www. sorting-algorithms. com/

Bubble Sort • Bubble Sort sorts by repeatedly comparing adjacent elements and swapping them if need be. It makes passes through the dataset until no swaps are needed. • It’s named Bubble because the data slowly ‘bubbles’ to its correct location.

Bubble Sort public void bubble. Sort(int[] arr) { boolean sorted = false; int j = 0; int temp; while (!sorted) { sorted = true; j++; for (int i = 0; i < arr. length - j; i++){ if (arr[i] > arr[i + 1]) { temp = arr[i]; arr[i] = arr[i + 1]; arr[i + 1] = temp; sorted= false; } }

Cost analysis Worst case n times through the main loop n + (n-1) + (n-2) +. . . = O(n^2) comparisons and swaps Best case the array is already sorted O(n) comparisons and swaps

Bubble Sort • Because Bubble Sort is so inefficient it is not used very often. It is however very simple to implement and can be fine for nearly sorted datasets as well as very small datasets.

Animation of Bubble Sort Notice the swaps. First we swap 6 and 5 because. Then we move forward and swap 6 and 3, followed by 6 and 1. This pattern continues till the end of the list. The list is then revisited and we continue looking for swaps until no swaps are performed in a pass and we know we have finished.

Insertion Sort • Insertion sort works by inserting an element into the already sorted subset of the data until there are no more elements left to sort. • Let’s take a look

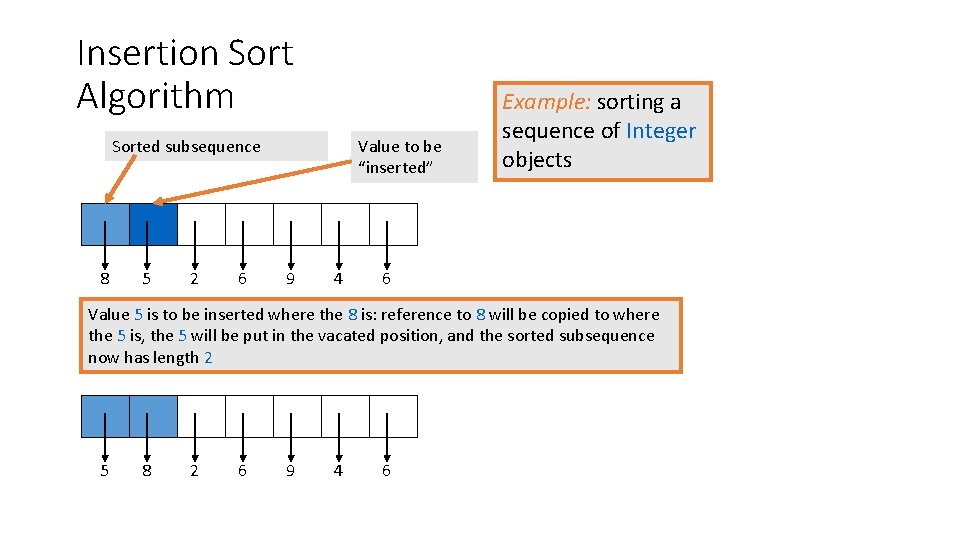
Insertion Sort Algorithm Sorted subsequence 8 5 2 6 Value to be “inserted” 9 4 Example: sorting a sequence of Integer objects 6 Value 5 is to be inserted where the 8 is: reference to 8 will be copied to where the 5 is, the 5 will be put in the vacated position, and the sorted subsequence now has length 2 5 8 2 6 9 4 6

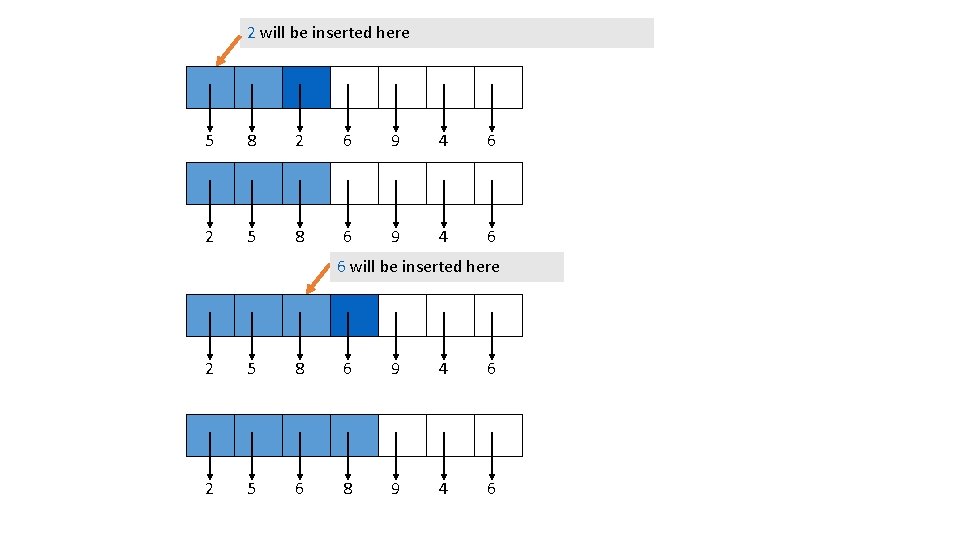
2 will be inserted here 5 8 2 6 9 4 6 2 5 8 6 9 4 6 6 will be inserted here 2 5 8 6 9 4 6 2 5 6 8 9 4 6

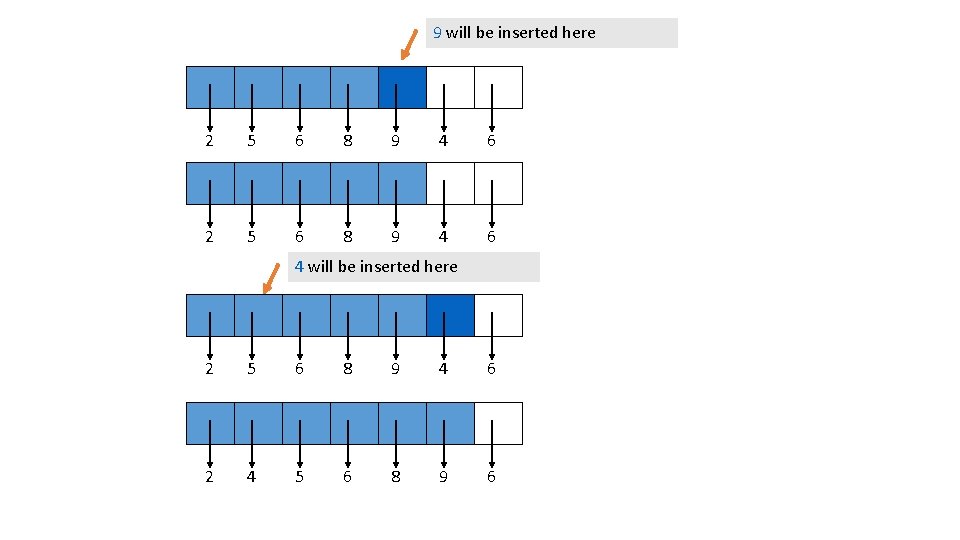
9 will be inserted here 2 5 6 8 9 4 6 4 will be inserted here 2 5 6 8 9 4 6 2 4 5 6 8 9 6

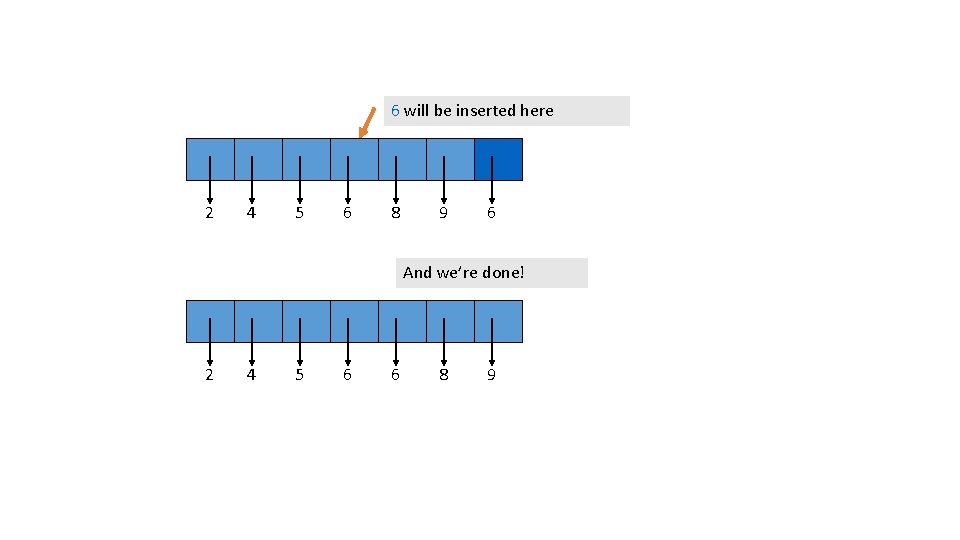
6 will be inserted here 2 4 5 6 8 9 6 And we’re done! 2 4 5 6 6 8 9

Insertion Sort • We will take a look at two ways of doing Insertion Sort • With stacks • With arrays

Insertion Sort using Stacks Approach to the problem: • Use two temporary stacks sorted and temp, both of which are originally empty • The contents of sorted will always be in order, with the smallest item on the top of the stack • This will be the “sorted subsequence” • temp will temporarily hold items that need to be “shifted” out in order to insert the new item in the proper place in sorted

Insertion Sort Using Stacks Algorithm • While the list is not empty • Remove the first item from the list • While sorted is not empty and the top of sorted is smaller than this item, pop the top of sorted and push it onto temp • push the current item onto sorted • While temp is not empty, pop its top item and push it onto sorted • The list is now empty, and sorted contains the items in ascending order from top to bottom • To restore the list, pop the items one at a time from sorted, and add to the rear of the list

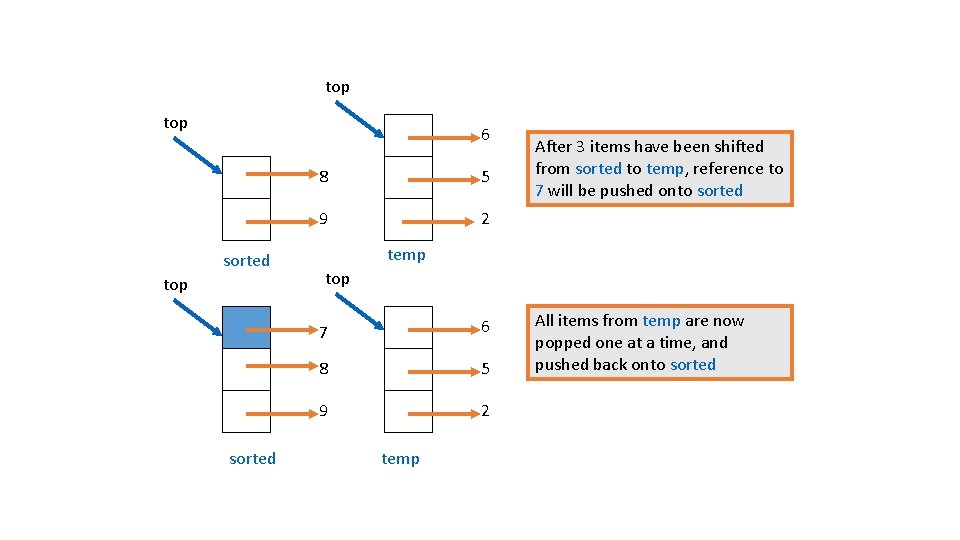
Insertion Sort Using Stacks top 7 2 5 A typical step in the sorting algorithm: 6 To add reference to 7 to sorted: pop items from sorted and push onto temp until sorted is empty, or top of sorted refers to a value >7 8 9 sorted temp <empty>

top 6 sorted top sorted 8 5 9 2 After 3 items have been shifted from sorted to temp, reference to 7 will be pushed onto sorted temp top 7 6 8 5 9 2 temp All items from temp are now popped one at a time, and pushed back onto sorted

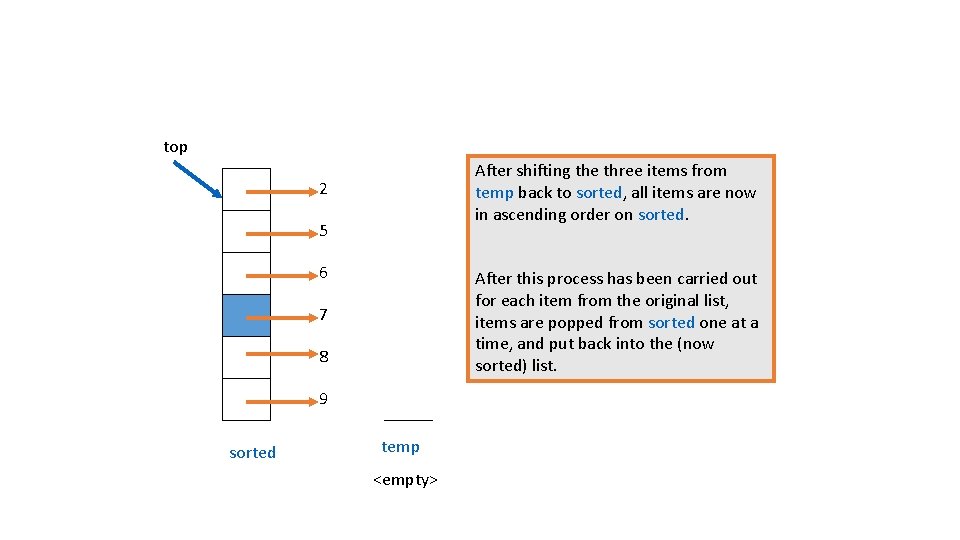
top After shifting the three items from temp back to sorted, all items are now in ascending order on sorted. 2 5 6 After this process has been carried out for each item from the original list, items are popped from sorted one at a time, and put back into the (now sorted) list. 7 8 9 sorted temp <empty>

Analysis of Insertion Sort Using Stacks • Roughly: nested loops on n items • So, what do you think the time complexity might be? • In more detail: analyze it in terms of the number of stack and list operations push, pop, remove. First, add. To. Rear

• Each time through the outer while loop, one more item is removed from the list and put into place on sorted: • Assume that there are k items in sorted. Worst case: every item has to be popped from sorted and pushed onto temp, so k pops and k pushes • New item is pushed onto sorted • Items in temp are popped and pushed onto sorted, so k pops and k pushes • So, total number of stack operations is 4*k + 1

• The outer while loop is executed n times, but each time the number of elements in sorted increases by 1, from 0 to (n-1) • So, the total number of stack operations in the outer while loop, in the worst case, is (4*0 + 1) + (4*1 + 1) + … + (4*(n-1) + 1) = 2 * n 2 – n • Then there are n additional pops to move the sorted items back onto the list (adding at the rear of the list) • So, the total number of stack operations is 2 * n 2

• Total number of stack operations is 2 * n 2 • Total number of list operations is 2 * n • In the outer while loop, remove. First is done n times • At the end, add. To. Rear is done n times to get the items back on the list • Total number of stack and list operations is 2 * n 2 + 2 *n • So, insertion sort using stacks is an O(n 2 ) algorithm

Complexity of Insertion Sort • When is the best case of our stack Insertion Sort? • When the list is already sorted but backwards! Insertion Sort in that case is O(n). • NOTE this is not the case for a general insertion sort • What is the worst case? • If the items are already sorted; why is the worst case for our stack Insertion Sort? • NOTE this is not the case for a general insertion sort

Animation of insertion sort

Insertion sort with arrays public static void insert. Sort(int[] A){ //loop through array for(int i = 1; i < A. length; i++){ // value we are current considering int value = A[i]; //index setting so we don’t check in non sorted portion of array int j = i - 1; } } while(j >= 0 && A[j] > value){ A[j + 1] = A[j]; j = j - 1; } A[j + 1] = value;

Complexity of Insertion Sort with arrays • When is the best case of the array Insertion sort? • When the array is already sorted! • When is the worst case? • When the array is sorted backwards! • NOTE: this is the complexity for insertion sort you should remember as it applies to the GENERAL insertion sort NOT just the stack version

Selection Sort • Selection Sort orders a sequence of values by repetitively putting a particular value into its final position • More specifically: • Find the smallest value in the sequence • Switch it with the value in the first position • Find the next smallest value in the sequence • Which will be the smallest if excluding the one in the first position • Switch it with the value in the second position • Repeat until all values are in their proper places

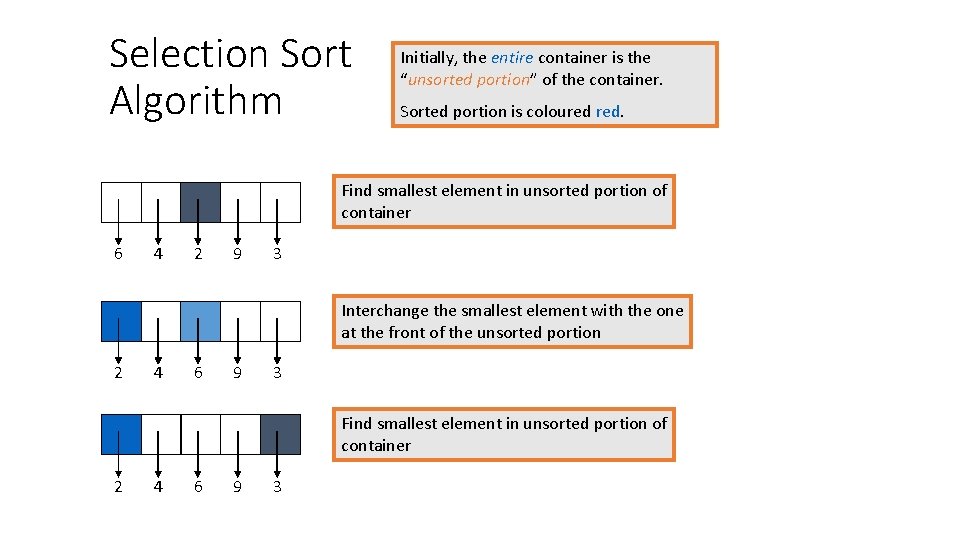
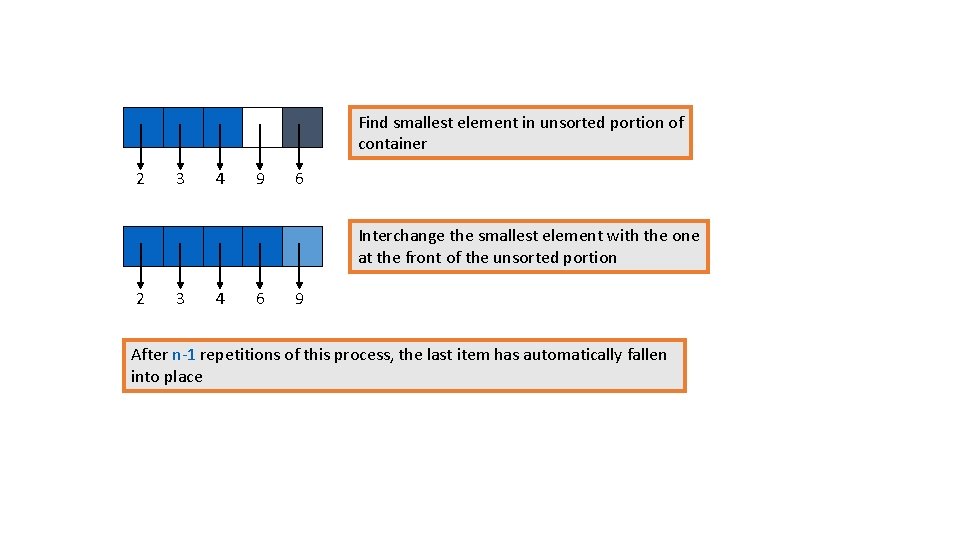
Selection Sort Algorithm Initially, the entire container is the “unsorted portion” of the container. Sorted portion is coloured red. Find smallest element in unsorted portion of container 6 4 2 9 3 Interchange the smallest element with the one at the front of the unsorted portion 2 4 6 9 3 Find smallest element in unsorted portion of container 2 4 6 9 3

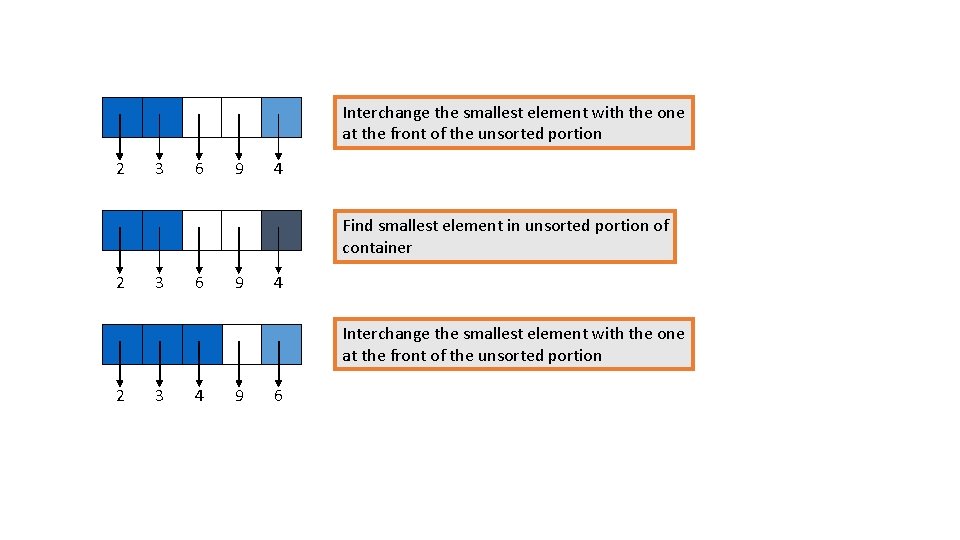
Interchange the smallest element with the one at the front of the unsorted portion 2 3 6 9 4 Find smallest element in unsorted portion of container 2 3 6 9 4 Interchange the smallest element with the one at the front of the unsorted portion 2 3 4 9 6

Find smallest element in unsorted portion of container 2 3 4 9 6 Interchange the smallest element with the one at the front of the unsorted portion 2 3 4 6 9 After n-1 repetitions of this process, the last item has automatically fallen into place

Animation of Selection Sort In this animation red is the current minimum, yellow is the sorted list and blue is the current item.

Selection Sort Using a Queue Approach to the problem: • Create a queue sorted, originally empty, to hold the items that have been sorted so far • The contents of sorted will always be in order, with new items added at the end of the queue

Selection Sort Using Queue Algorithm • While the unordered list is not empty: • remove the smallest item from list and enqueue it to the end of sorted • The list is now empty, and sorted contains the items in ascending order, from front to rear • To restore the original list, dequeue the items one at a time from sorted, and add them to the rear of list

• Now we will refine the step remove the smallest item from list and enqueue it to the end of sorted • We will call this step move. Smallest • It will use a second queue temp for temporary storage

move. Smallest smallest. So. Far = first item in list (remove. First) While list is not empty { remove. First item from list If item is less than smallest. So. Far { enqueue smallest. So. Far to end of temp smallest. So. Far = item } Else enqueue item to temp }

move. Smallest • list will now be empty, smallest. So. Far contains the smallest item, and temp contains all the other items • enqueue smallest. So. Far to the end of sorted • dequeue the items one at a time from temp, and add them to the rear of list (a while loop)

Analysis of Selection Sort Using Queue • Analyze it in terms of the number of queue and list operations enqueue, dequeue, remove. First, add. To. Rear • Each time move. Smallest is called, one more item is moved out of the original list and put into place in the queue sorted • Assume there are k items in the list; inside move. Smallest we have: • • • remove. First before the first while loop k-1 remove. Firsts and k-1 enqueues inside 1 st while loop 1 enqueue (of smallest. So. Far) k-1 dequeues and k-1 add. To. Rears inside 2 nd while loop So, total number of queue and list operations is 4*k -2

• Now let’s look at the whole algorithm: • It calls move. Smallest n times, and the number of elements in list ranges from n down to 1 • So, the number of list and queue operations in the first loop is (4*n– 2) + (4*(n-1)– 2) + … + (4*2– 2) + (4*1– 2) = 4*(n*(n + 1) / 2) – 2*n = 2*n 2 • Number of list and queue operations in the second loop is 2*n • Total number of list and queue operations is 2*n 2 + 2*n • So, Selection Sort is an O(n 2) algorithm

Discussion • Is there a best case? • No, we have to step through the entire remainder of the list looking for the next smallest item, no matter what the ordering • Is there a worst case? • No

Selection sort with arrays public static void sort(int[] nums){ for(int current. Place = 0; current. Place<nums. length-1; current. Place++){ int smallest = Integer. MAX_VALUE; int smallest. At = current. Place+1; for(int check = current. Place; check<nums. length; check++){ if(nums[check]<smallest){ smallest. At = check; smallest = nums[check]; } } int temp = nums[current. Place]; nums[current. Place] = nums[smallest. At]; nums[smallest. At] = temp; } }

Quick Sort • Quick Sort orders a sequence of values by partitioning the list around one element (called the pivot or partition element), then sorting each partition • More specifically: • Choose one element in the sequence to be the pivot • Organize the remaining elements into two groups (partitions): those greater than the pivot and those less than the pivot • Then sort each of the partitions (recursively)

Quick Sort • partition element or pivot: • The choice of the pivot is arbitrary • For efficiency, it would be nice if the pivot divided the sequence roughly in half • However, the algorithm will work in any case • But…. . More on this later

Quick Sort Approach to the problem: • We put all the items to be sorted into a container (e. g. an array, a collection) • We will call the container operations get and put • We choose the pivot (partition element) at random from the container • We use a container smaller to hold the items that are smaller than the pivot, and a container bigger to hold the items that are larger than the pivot • We then recursively sort the items in the containers smaller and bigger

Quick Sort Algorithm • Remove the items to be sorted from the list and put them into an empty container • If the container is not empty • pivot = one item from the container, chosen at random (get) • Create containers smaller and bigger, originally empty • While the container is not empty • Get an item from the container • If pivot < item, put item into bigger otherwise put item into smaller • Sort smaller • Add pivot at rear of list • Sort bigger

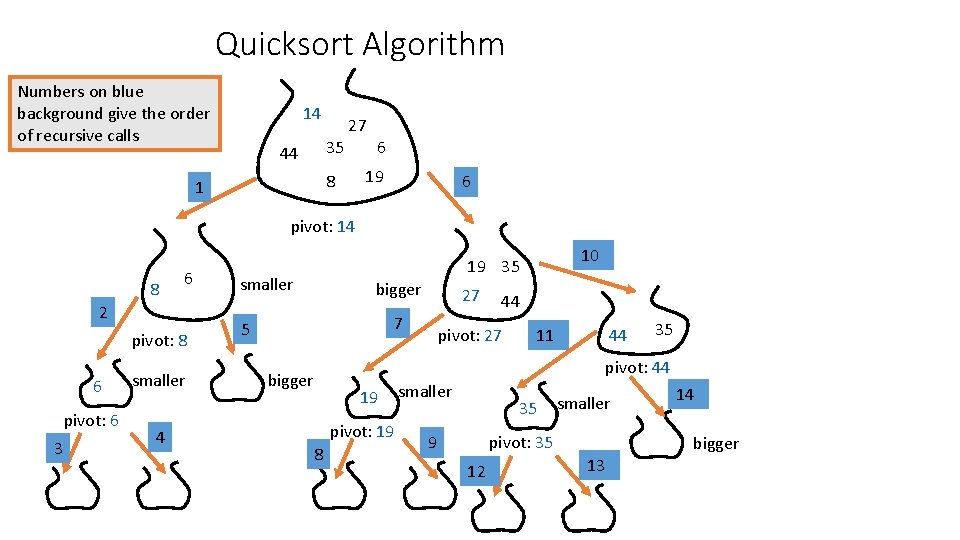
Quicksort Algorithm Numbers on blue background give the order of recursive calls 14 27 35 44 8 1 6 19 6 pivot: 14 8 6 2 pivot: 8 6 pivot: 6 3 smaller 4 10 19 35 smaller bigger 27 7 5 44 pivot: 27 11 44 35 pivot: 44 bigger 19 pivot: 19 8 smaller 35 smaller pivot: 35 9 12 13 14 bigger

Analysis of Quick Sort • We will look at two cases for Quick Sort : • Worst case • When the pivot element is the largest or smallest item in the container • why is the worst case? • Best case • When the pivot element is the middle item • why is the best case?

• To simplify things, we will do the analysis only in terms of the number of get operations needed to sort an initial container of n items, T(n) • We could also include the put operations – but why can we leave them out? • In the interest of fairness of comparison with the other sorting methods, we should also consider that the unsorted items started in a list and should end in the list - we will discuss this later

Worst Case Analysis: • Assume that the pivot is the largest item in the bag • If n is 0, there are no operations, so T(0)=0 • If n > 0, the pivot is removed from the container (get) and the remaining n-1 items are redistributed (get, put) into two containers: • smaller is of size n-1 • bigger is of size 0 • So, the number of get operations for this step is 1 + (n-1)

• Then we have two recursive calls: • Sort smaller, which is of size n-1 • Sort bigger, which is of size 0 • So, T(n) = 1 + (n-1) + T(0) • But, the number of get operations required to sort a container of size 0 is 0 • And, the number of get operations required to sort a container of size k in general is T(k) = 1 + (k-1) + (the number of get operations needed to sort a container of size k-1) = k + T(k-1)

• So, the total number of get operations T(n) for the sort is T(n) = n + T(n-1) = n + (n-1) + T(n-2) = n + (n-1) + (n-2) + … + 2 + 1 + T(0) = n*(n+1)/2 = n 2 / 2 + n / 2 • So, the worst case time complexity of Quick Sort is O(n 2)

Discussion • Let’s now also consider the operations needed to get the n items from the original list into the container: n remove. First operations, n put operations • We also have the operations needed to get the n items from the container at the end, and add them at the rear of the list • Will considering these operations change the time complexity of our Quick Sort?

Best Case Analysis • The best case occurs when the pivot element is chosen so that the two new containers are as close as possible to having the same size • Again, we would consider only the get operations • For a container of size n there are 1 + (n-1) = n get operations before the recursive calls are encountered • Each of the two recursive calls will sort a container that contains at most n/2 items

• It is beyond the scope of this course to do the analysis, but it turns out that the best case time complexity for Quick Sort is O(n log 2 n) • And it turns out that the average time complexity for Quick Sort is the same

Quick sort using arrays Left will start as 0 right as the last element in array This version sets the pivot to be half way in the array. public static int partition(int arr[], int left, int right) { int i = left, j = right; int tmp; int pivot = arr[(left + right) / 2]; while (i <= j) { while (arr[i] < pivot) i++; while (arr[j] > pivot) j--; if (i <= j) { tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; i++; j--; } }; public static void quick. Sort(int arr[], int left, int right) { int index = partition(arr, left, right); if (left < index - 1) quick. Sort(arr, left, index - 1); if (index < right) quick. Sort(arr, index, right); } } return i;

Animation of quick sort

Heap sort •

Example The heap with 9 nodes

The heap property When storing comparable's in a heap, ensure that: the value of the element at a node is greater than, or equal to, the value of the elements at its two children the value at a node is less than, or equal to, the value at its parent.

Building a heap •

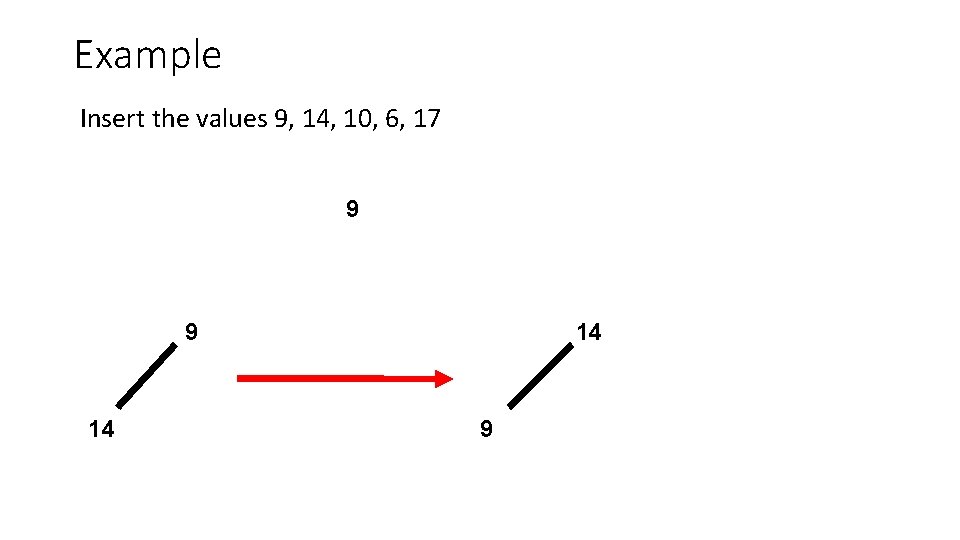
Example Insert the values 9, 14, 10, 6, 17 9 9 14 14 9

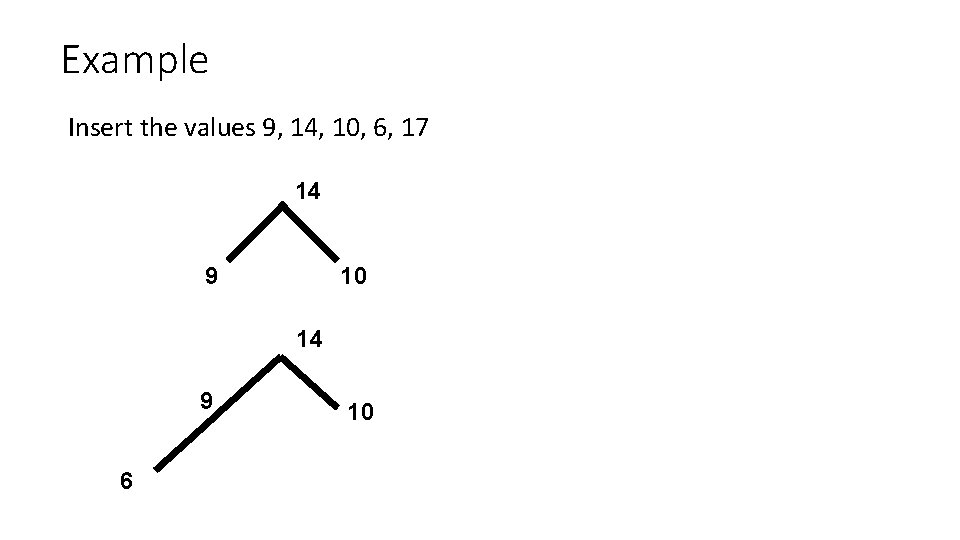
Example Insert the values 9, 14, 10, 6, 17 14 9 10 14 9 6 10

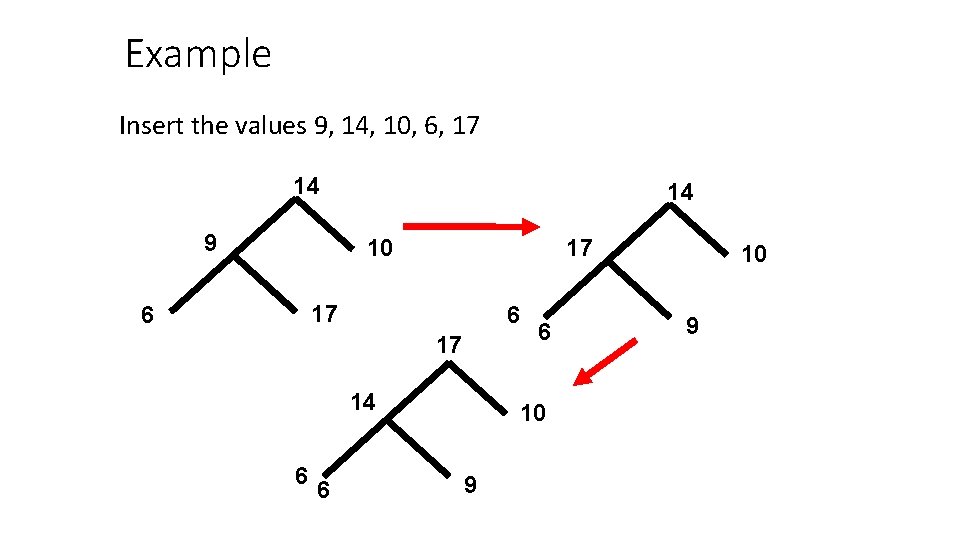
Example Insert the values 9, 14, 10, 6, 17 14 9 14 10 17 17 6 6 17 14 6 6 6 10 9

Removing the largest element remove the root place the smallest element at the root and bubble it down: In other words: if not a heap, swap it with the largest of its children continue until you get a heap

Cost for a heap with n elements: the height of the tree is O(log(n)) insert and remove an element on a path from the root to a leaf so both take O(log(n)) operations

Data representation The most common implementation uses an array For a heap with n element, indices range from 0 to n-1 Easy access to parent and children: left child(i) = 2 i+1 right child(i) = 2 i+2 parent(i) = (i-1)/2

Heap sort Simple algorithm: create an empty heap insert all elements Repeat remove the largest until the heap is empty Cost for n elements (best case AND worst case): O(n log(n))

Heap Sort with arrays public static void heap. Sort(int[] a){ int count = a. length; //first place a in max-heap order heapify(a, count); int end = count - 1; while(end > 0){ //swap the root(maximum value) of the heap with the //last element of the heap int tmp = a[end]; a[end] = a[0]; a[0] = tmp; //put the heap back in max-heap order sift. Down(a, 0, end - 1); //decrement the size of the heap so that the previous //max value will stay in its proper place end--; }

Heap Sort with arrays cont. public static void heapify(int[] a, int count){ //start is assigned the index in a of the last parent node int start = (count - 2) / 2; //binary heap } while(start >= 0){ //sift down the node at index start to the proper place //such that all nodes below the start index are in heap //order sift. Down(a, start, count - 1); start--; } //after sifting down the root all nodes/elements are in heap order

Heap Sort with arrays cont. public static void sift. Down(int[] a, int start, int end){ //end represents the limit of how far down the heap to sift int root = start; } while((root * 2 + 1) <= end){ //While the root has at least one child int child = root * 2 + 1; //root*2+1 points to the left child //if the child has a sibling and the child's value is less than its sibling's. . . if(child + 1 <= end && a[child] < a[child + 1]) child = child + 1; //. . . then point to the right child instead if(a[root] < a[child]){ //out of max-heap order int tmp = a[root]; a[root] = a[child]; a[child] = tmp; root = child; //repeat to continue sifting down the child now }else return; }

Animation of Heap Sort

Summary • Insertion Sort is O(n 2) • Selection Sort is O(n 2) • Quick Sort is (if we do it right!) O(nlog 2 n) • Heap Sort is O(nlog 2 n) • Which one would you choose? When and why?