Sorting Types of Sorting Internal Sort Main Memory

Types of Sorting �Internal Sort Main Memory �E. g. Bubble sort �Selection exchange �Shell

Sorting Stability �Repetitive records should sort properly and in same order. �E. G. Employee

Efficiency �Compare Various Techniques with respect to Time Complexity. �Compare No. of Passes required

�Sorting takes an unordered collection and makes it an ordered one. 1 2 3

"Bubbling Up" the Largest Element �Traverse a collection of elements �Move from the front

2. Flag=0 Loop: j=1 To E 1. 2. 3. 4. If A(j)>A(j+1) Then Swap

LB No, Swap isn’t built in. Procedure Swap(a, b) t isoftype Num t <-

items of Interest �Notice that only the largest value is correctly placed �All other

Repeat “Bubble Up” How Many Times? �If we have N elements… �And if each

N-1 “Bubbling” All the Elements 1 42 2 35 3 12 4 77 5

Reducing the Number of Comparisons 1 77 1 42 2 35 3 12 4

Reducing the Number of Comparisons �On the Nth “bubble up”, we only need to

N is … // Size of Array Arr_Type definesa Array[1. . N] of Num

Outer loop exitif(to_do = 0) index <- 1 loop exitif(index > to_do) if(A[index] >

Already Sorted Collections? �What if the collection was already sorted? �What if only a

Using a Boolean “Flag” �We can use a boolean variable to deteriteme if any

did_swap isoftype Boolean did_swap <- true loop exitif ((to_do = 0) OR NOT(did_swap)) index

An Animated Example N 8 to_do 7 did_swap true index 98 23 45 14

An Animated Example N 8 to_do 7 index 1 did_swap false 98 23 45

An Animated Example N 8 to_do 7 index 1 did_swap false Swap 98 23

An Animated Example N 8 to_do 7 index 1 did_swap true Swap 23 98

An Animated Example N 8 to_do 7 index 2 did_swap 23 98 45 14

An Animated Example N 8 to_do 7 index 2 did_swap true Swap 23 98

An Animated Example N 8 to_do 7 index 2 did_swap true Swap 23 45

An Animated Example N 8 to_do 7 index 3 did_swap 23 45 98 14

An Animated Example N 8 to_do 7 index 3 did_swap true Swap 23 45

An Animated Example N 8 to_do 7 index 4 did_swap 23 45 14 98

An Animated Example N 8 to_do 7 index 4 did_swap true Swap 23 45

An Animated Example N 8 to_do 7 index 5 did_swap 23 45 14 6

An Animated Example N 8 to_do 7 index 5 did_swap true Swap 23 45

An Animated Example N 8 to_do 7 index 6 did_swap 23 45 14 6

An Animated Example N 8 to_do 7 index 6 did_swap true Swap 23 45

An Animated Example N 8 to_do 7 index 7 did_swap 23 45 14 6

An Animated Example N 8 to_do 7 index 7 did_swap true Swap 23 45

After First Pass of Outer Loop N 8 to_do 7 index 8 did_swap Finished

The Second “Bubble Up” N 8 to_do 6 index 1 did_swap false 23 45

The Second “Bubble Up” N 8 to_do 6 index 1 did_swap false No Swap

The Second “Bubble Up” N 8 to_do 6 index 2 did_swap false 23 45

The Second “Bubble Up” N 8 to_do 6 index 2 did_swap false Swap 23

The Second “Bubble Up” N 8 to_do 6 index 2 did_swap true Swap 23

The Second “Bubble Up” N 8 to_do 6 index 3 did_swap 23 14 45

The Second “Bubble Up” N 8 to_do 6 index 3 did_swap true Swap 23

The Second “Bubble Up” N 8 to_do 6 index 4 did_swap 23 14 6

The Second “Bubble Up” N 8 to_do 6 index 4 did_swap true No Swap

The Second “Bubble Up” N 8 to_do 6 index 5 did_swap 23 14 6

The Second “Bubble Up” N 8 to_do 6 index 5 did_swap true Swap 23

The Second “Bubble Up” N 8 to_do 6 index 6 did_swap 23 14 6

The Second “Bubble Up” N 8 to_do 6 index 6 did_swap true Swap 23

After Second Pass of Outer Loop N 8 to_do 6 index 7 did_swap Finished

The Third “Bubble Up” N 8 to_do 5 index 1 did_swap false 23 14

The Third “Bubble Up” N 8 to_do 5 index 1 did_swap false Swap 23

The Third “Bubble Up” N 8 to_do 5 index 1 did_swap true Swap 14

The Third “Bubble Up” N 8 to_do 5 index 2 did_swap 14 23 6

The Third “Bubble Up” N 8 to_do 5 index 2 did_swap true Swap 14

The Third “Bubble Up” N 8 to_do 5 index 3 did_swap 14 6 1

The Third “Bubble Up” N 8 to_do 5 index 3 did_swap true No Swap

The Third “Bubble Up” N 8 to_do 5 index 4 did_swap 14 6 1

The Third “Bubble Up” N 8 to_do 5 index 4 did_swap true Swap 14

The Third “Bubble Up” N 8 to_do 5 index 5 did_swap 14 6 1

The Third “Bubble Up” N 8 to_do 5 index 5 did_swap true Swap 14

After Third Pass of Outer Loop N 8 to_do 5 index 6 did_swap Finished

The Fourth “Bubble Up” N 8 to_do 4 index 1 did_swap false 14 6

The Fourth “Bubble Up” N 8 to_do 4 index 1 did_swap false Swap 14

The Fourth “Bubble Up” N 8 to_do 4 index 1 did_swap true Swap 6

The Fourth “Bubble Up” N 8 to_do 4 index 2 6 1 did_swap true

The Fourth “Bubble Up” N 8 to_do 4 index 2 did_swap true No Swap

The Fourth “Bubble Up” N 8 to_do 4 index 3 6 1 did_swap true

The Fourth “Bubble Up” N 8 to_do 4 index 3 did_swap true No Swap

The Fourth “Bubble Up” N 8 to_do 4 index 4 6 1 did_swap true

The Fourth “Bubble Up” N 8 to_do 4 index 4 did_swap true No Swap

After Fourth Pass of Outer Loop N 8 to_do 4 index 5 6 1

The Fifth “Bubble Up” N 8 to_do 3 index 1 6 1 did_swap false

The Fifth “Bubble Up” N 8 to_do 3 index 1 did_swap false No Swap

The Fifth “Bubble Up” N 8 to_do 3 index 2 6 1 did_swap false

The Fifth “Bubble Up” N 8 to_do 3 index 2 did_swap false No Swap

The Fifth “Bubble Up” N 8 to_do 3 index 3 6 1 did_swap false

The Fifth “Bubble Up” N 8 to_do 3 index 3 did_swap false No Swap

After Fifth Pass of Outer Loop N 8 to_do 3 index 4 6 1

Finished “Early” N 8 to_do 3 index 4 did_swap false We didn’t do any

Time Complexity �Best Case n � Average Case n 2 �Worst Case n 2

Insertion Sort �while some elements unsorted: �Using linear search, find the location in the

Insertion Sort 45 38 45 60 60 66 45 66 79 47 13 74

40 60 30 20 item = 60 40 60 30 i j 20 item

Pseudo-code Procedure_Insertion sort(a, n) start 1. Loop: j=1 To n 1. 2. 3. item=a[j]

Time complexity �Best case: n – Linear �Average Case n 2 �Worst case n(n+1)/2

At start min=a[0]=40 40 60 30 20 min= 30 40 60 30 20 min

Pseudo-code Procedure_selection sort(a, n) start 1. Loop: i=0 To n-1 min =i; Loop: j=1

Time Complexity_ Selection �Best Case n 2 �Average Case n 2 �Worst Case n

Divide and Conquer �Divide and Conquer cuts the problem in half each time, but

Merging �The key to Merge Sort is merging two sorted lists into one, such

Merging X: Resul t: 3 10 (cont. ) 23 54 Y: 1 5 25

Merging X: Resul t: 3 10 1 (cont. ) 23 54 Y: 5 25

Merging X: Resul t: (cont. ) 10 1 23 3 54 Y: 5 25

Merging X: Resul t: (cont. ) 10 1 54 Y: 23 3 5 25

Merging (cont. ) X: Resul t: 54 Y: 23 1 3 5 10 25

Merging (cont. ) X: Resul t: 54 Y: 1 3 5 10 25 23

Merging (cont. ) X: Resul t: 54 Y: 1 3 5 10 75 23

Merging (cont. ) X: Resul t: Y: 1 3 5 10 75 23 25

Merging (cont. ) X: Resul t: Y: 1 3 5 10 23 25 54

Merge sort -A divide-and-conquer algorithm: �Divide the unsorted array into 2 halves until the

98 23 45 14 98 23 Merge 45 14 6 67 33 42

98 23 45 14 98 23 23 Merge 45 14 6 67 33 42

98 23 45 14 98 23 23 98 Merge 45 14 6 67 33

98 23 45 14 98 23 23 98 45 14 6 67 33 42

98 23 45 14 98 23 23 98 45 14 14 Merge 6 67

98 23 45 14 98 23 23 98 45 14 14 45 Merge 6

98 23 45 14 98 23 23 98 45 14 14 45 14 Merge

98 23 45 14 98 23 23 98 45 14 14 45 14 23

98 23 45 14 98 23 23 98 45 14 14 45 6 67

98 23 45 14 6 67 33 42 98 23 45 14 98 23

Algorithm Mergesort(Passed an array) if array size > 1 Divide array in half Call

Pseudo code Mergesort(A, low, high) If (low<high)then { Mid: = (low+high)/2 //split list in

Merge(A[0…n-1], low, mid, high) k=low i=low j= mid+1 Loop: while(i<=mid &&j<=high) do if(A[i]<=A[j]) then

//copy remaining elements of left part(sublist 1) while(i<=mid)d 0 temp[k]=A[i] increment i Increment k

Summary �Divide the unsorted collection into two �Until the sub-arrays only contain one element

Slides: 169

Download presentation

Sorting

Types of Sorting �Internal Sort Main Memory �E. g. Bubble sort �Selection exchange �Shell Sort �Insertion Sort �Quick Sort etc. �External Sort Disk

Sorting Stability �Repetitive records should sort properly and in same order. �E. G. Employee database (Bob, Manager) (Bob, Team Leader) �(Bob, Manager) (John, Worker) �(John, Worker) (Mery, P. A) �(Bob, Team Leader) �(Mery, P. A)

Efficiency �Compare Various Techniques with respect to Time Complexity. �Compare No. of Passes required for sorting

Bubble Sort

�Sorting takes an unordered collection and makes it an ordered one. 1 2 3 4 5 6 77 42 35 12 101 5 1 2 3 4 5 6 5 12 35 42 77 101

"Bubbling Up" the Largest Element �Traverse a collection of elements �Move from the front to the end �“Bubble” the largest value to the end using pairwise comparisons and swapping 1 2 3 4 5 6 77 42 35 12 101 5

2. Flag=0 Loop: j=1 To E 1. 2. 3. 4. If A(j)>A(j+1) Then Swap A(j), A(j+1) Flag=1 Loop end j E=E-1 While End 4. Exit Outer loop 1. Inner loop bubble sort 1. Flag=1 2. E=N-1 3. While Flag=1

LB No, Swap isn’t built in. Procedure Swap(a, b) t isoftype Num t <- a a <- b b <- t endprocedure // Swap

items of Interest �Notice that only the largest value is correctly placed �All other values are still out of order �So we need to repeat this process 1 2 3 4 5 6 42 35 12 77 5 101 Largest value correctly placed

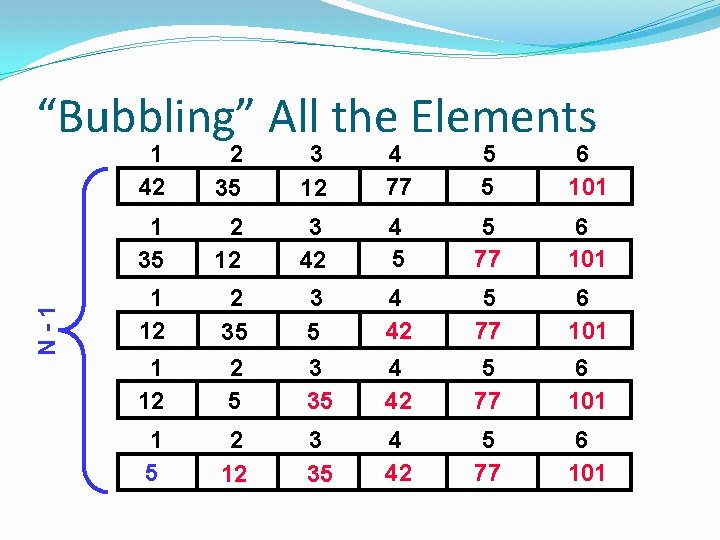
Repeat “Bubble Up” How Many Times? �If we have N elements… �And if each time we bubble an element, we place it in its correct location… �Then we repeat the “bubble up” process N – 1 times. �This guarantees we’ll correctly place all N elements.

N-1 “Bubbling” All the Elements 1 42 2 35 3 12 4 77 5 5 6 101 1 35 2 12 3 42 4 5 5 77 6 101 1 12 3 5 3 35 4 42 5 77 6 101 1 12 2 35 2 5 4 42 5 77 6 101 1 5 2 12 3 35 4 42 5 77 6 101

Reducing the Number of Comparisons 1 77 1 42 2 35 3 12 4 77 5 101 5 5 6 101 1 35 2 12 3 42 4 5 5 77 6 101 1 12 2 35 2 5 3 35 4 42 5 77 6 101 1 12

Reducing the Number of Comparisons �On the Nth “bubble up”, we only need to do MAX-N comparisons. �For example: �This is the 4 th “bubble up” �MAX is 6 �Thus we have 2 comparisons to do 1 12 2 35 3 5 4 42 5 77 6 101

Putting It All Together

N is … // Size of Array Arr_Type definesa Array[1. . N] of Num Procedure Swap(n 1, n 2 isoftype in/out Num) temp isoftype Num temp <- n 1 <- n 2 <- temp endprocedure // Swap

Outer loop exitif(to_do = 0) index <- 1 loop exitif(index > to_do) if(A[index] > A[index + 1]) then Swap(A[index], A[index + 1]) endif index <- index + 1 endloop to_do <- to_do - 1 endloop endprocedure // Bubblesort Inner loop procedure Bubblesort(A isoftype in/out Arr_Type) to_do, index isoftype Num to_do <- N – 1

Already Sorted Collections? �What if the collection was already sorted? �What if only a few elements were out of place and after a couple of “bubble ups, ” the collection was sorted? �We want to be able to detect this and “stop early”! 1 2 3 4 5 42 77 5 12 35 6 101

Using a Boolean “Flag” �We can use a boolean variable to deteriteme if any swapping occurred during the “bubble up. ” �If no swapping occurred, then we know that the collection is already sorted! �This boolean “flag” needs to be reset after each “bubble up. ”

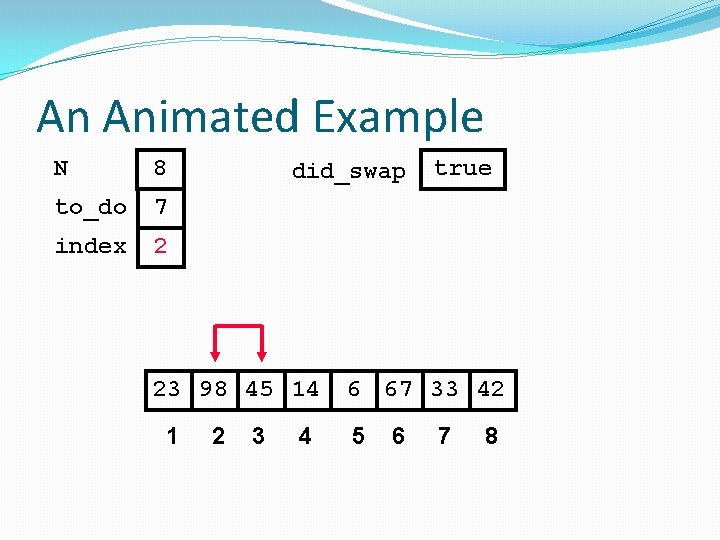
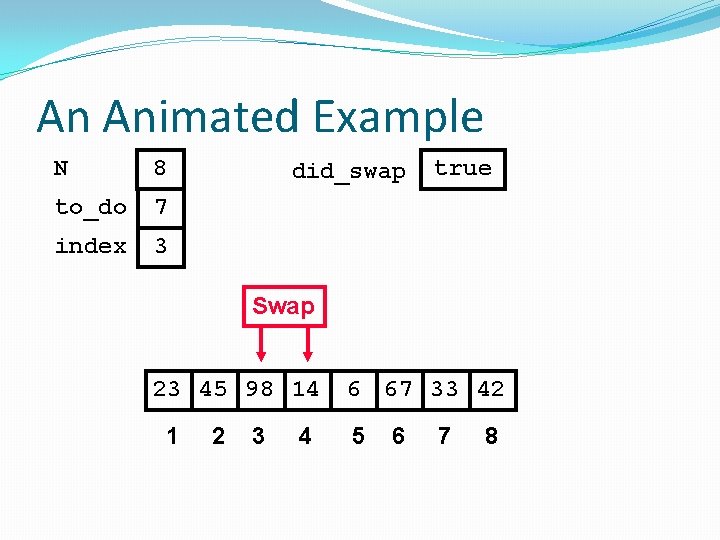
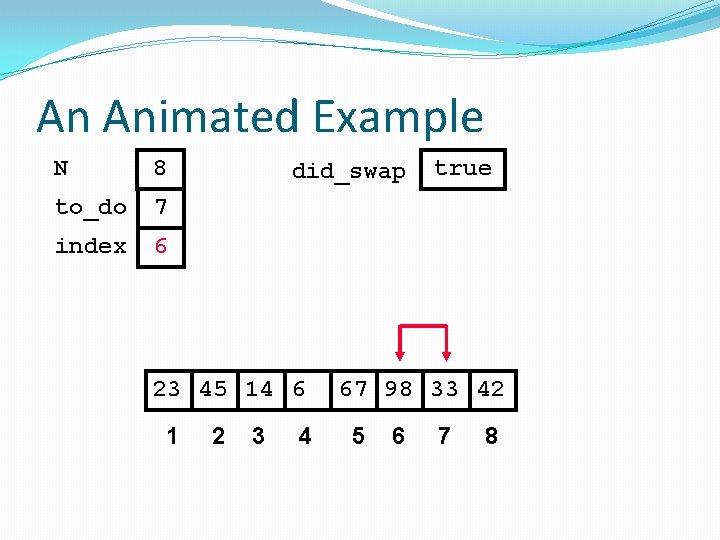
did_swap isoftype Boolean did_swap <- true loop exitif ((to_do = 0) OR NOT(did_swap)) index <- 1 did_swap <- false loop exitif(index > to_do) if(A[index] > A[index + 1]) then Swap(A[index], A[index + 1]) did_swap <- true endif index <- index + 1 endloop to_do <- to_do - 1 endloop

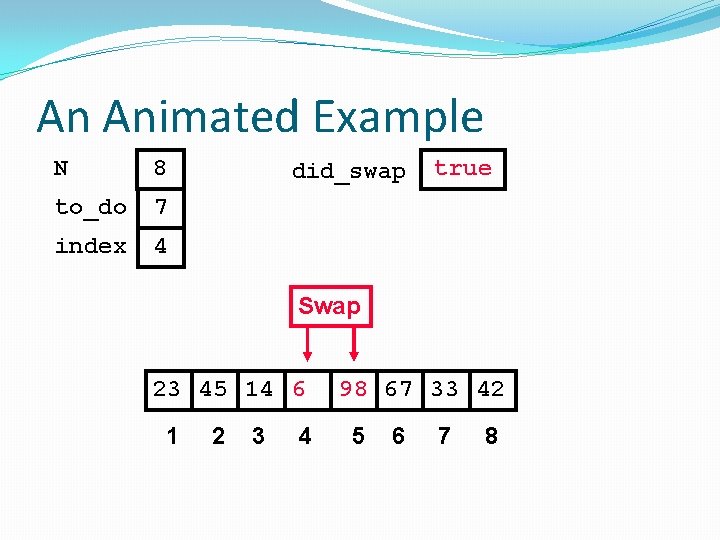
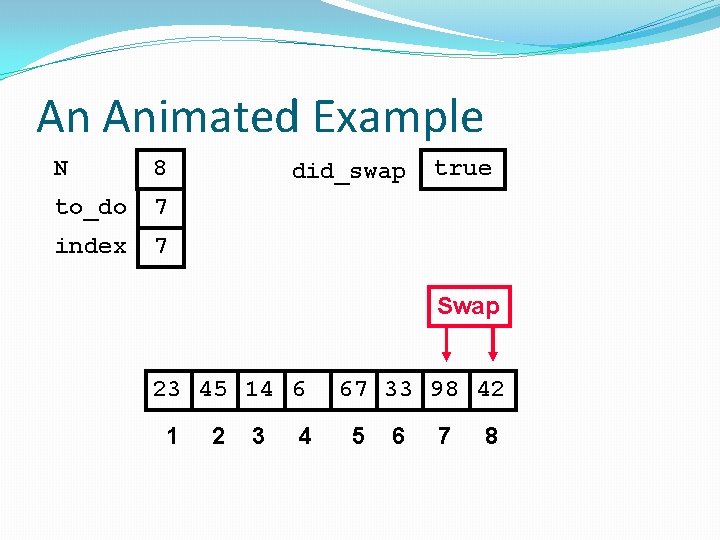
An Animated Example N 8 to_do 7 did_swap true index 98 23 45 14 1 2 3 4 6 67 33 42 5 6 7 8

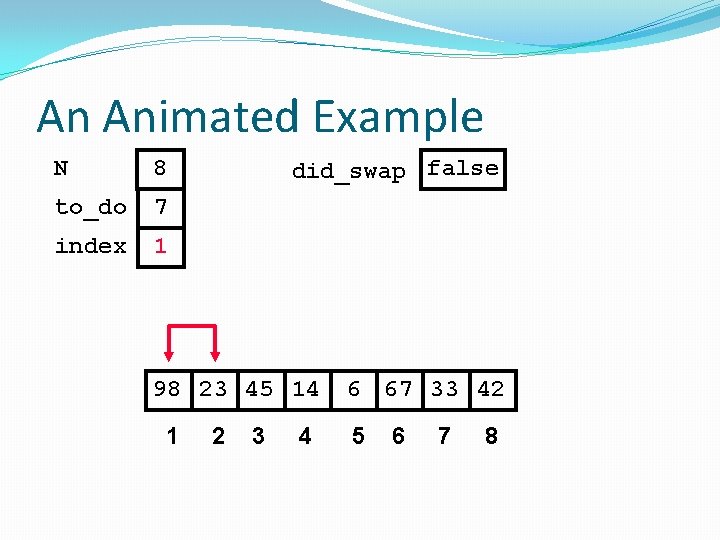
An Animated Example N 8 to_do 7 index 1 did_swap false 98 23 45 14 1 2 3 4 6 67 33 42 5 6 7 8

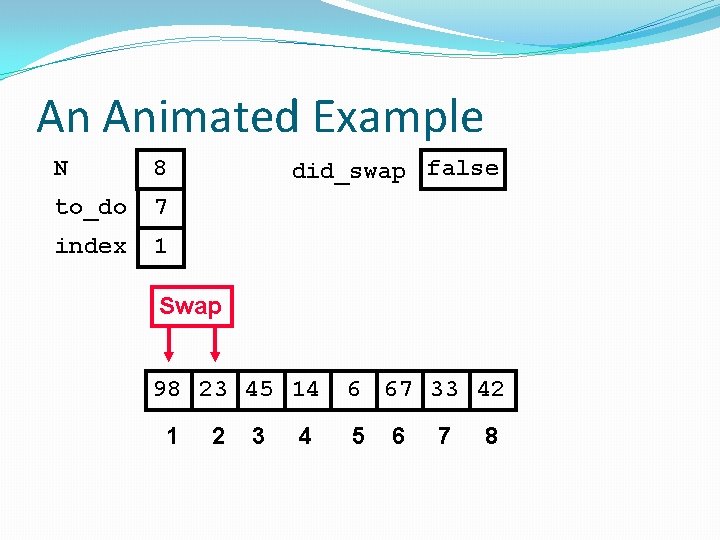
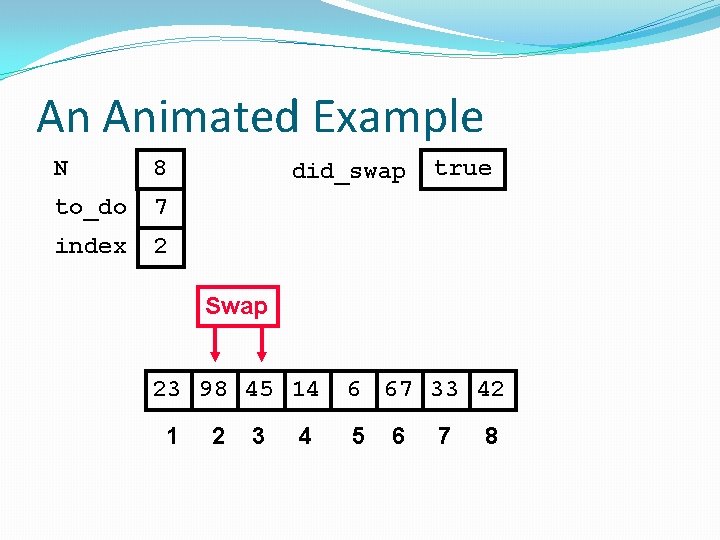
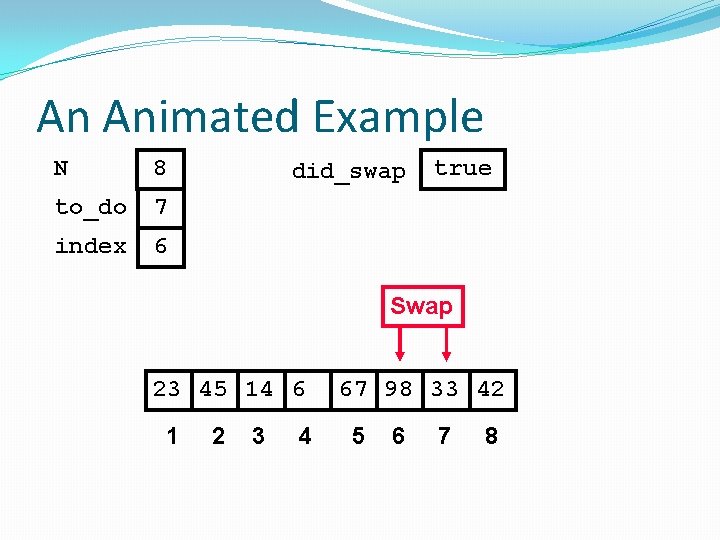
An Animated Example N 8 to_do 7 index 1 did_swap false Swap 98 23 45 14 1 2 3 4 6 67 33 42 5 6 7 8

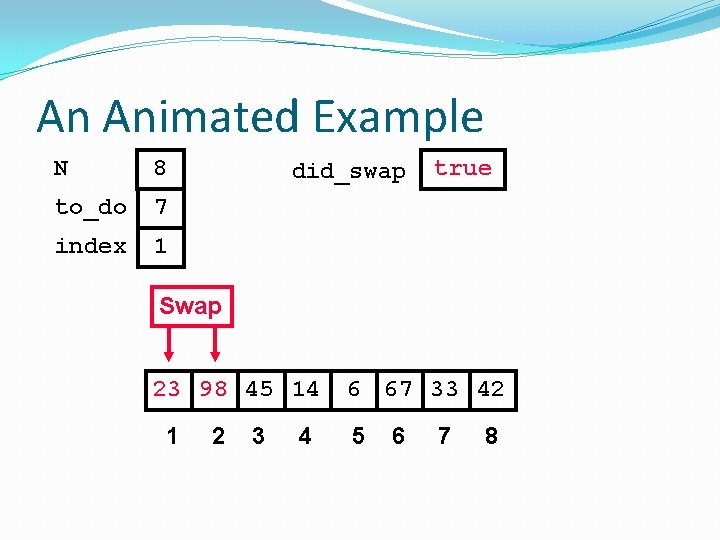
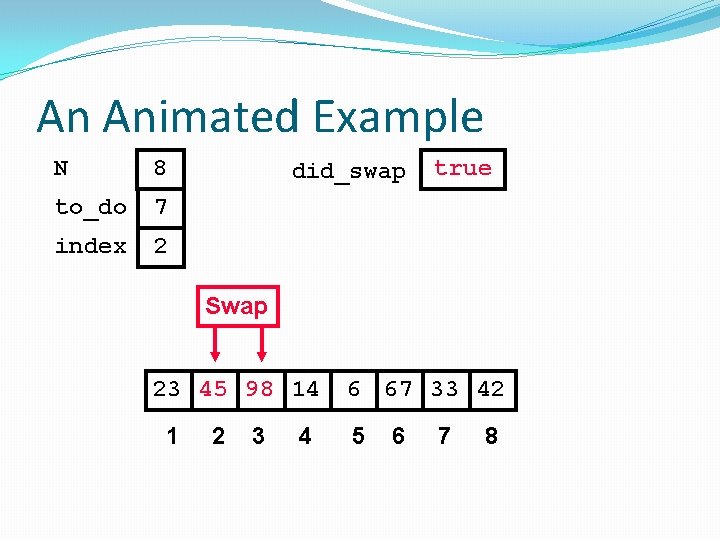
An Animated Example N 8 to_do 7 index 1 did_swap true Swap 23 98 45 14 1 2 3 4 6 67 33 42 5 6 7 8

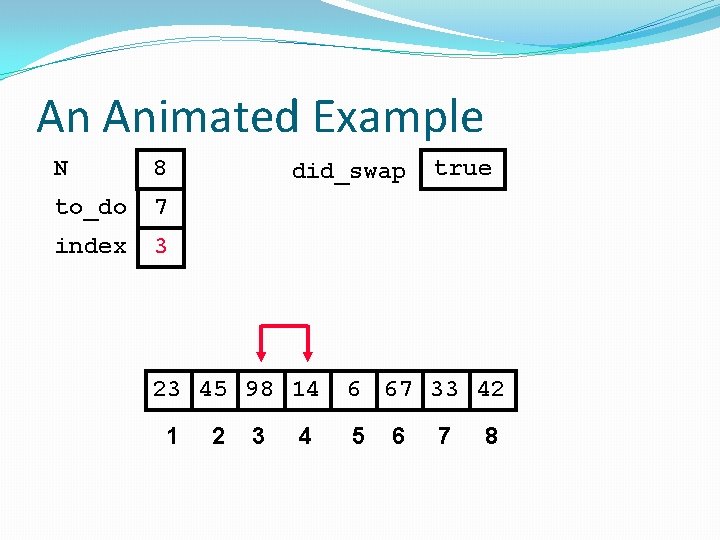
An Animated Example N 8 to_do 7 index 2 did_swap 23 98 45 14 1 2 3 4 true 6 67 33 42 5 6 7 8

An Animated Example N 8 to_do 7 index 2 did_swap true Swap 23 98 45 14 1 2 3 4 6 67 33 42 5 6 7 8

An Animated Example N 8 to_do 7 index 2 did_swap true Swap 23 45 98 14 1 2 3 4 6 67 33 42 5 6 7 8

An Animated Example N 8 to_do 7 index 3 did_swap 23 45 98 14 1 2 3 4 true 6 67 33 42 5 6 7 8

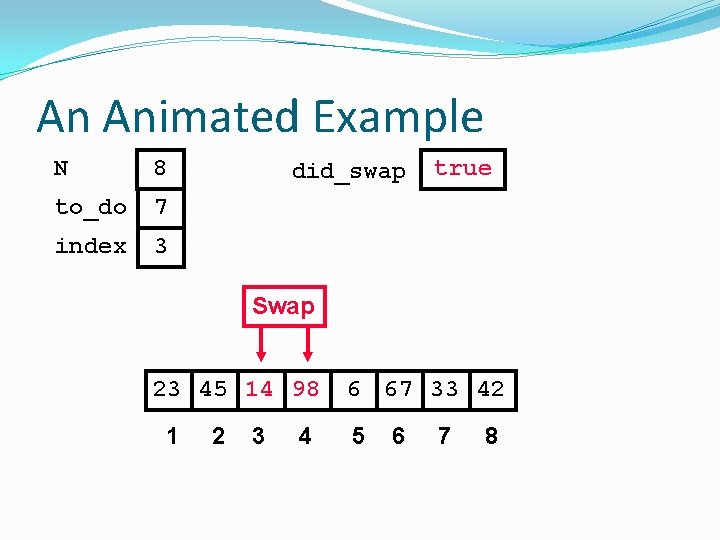
An Animated Example N 8 to_do 7 index 3 did_swap true Swap 23 45 98 14 1 2 3 4 6 67 33 42 5 6 7 8

An Animated Example N 8 to_do 7 index 3 did_swap true Swap 23 45 14 98 1 2 3 4 6 67 33 42 5 6 7 8

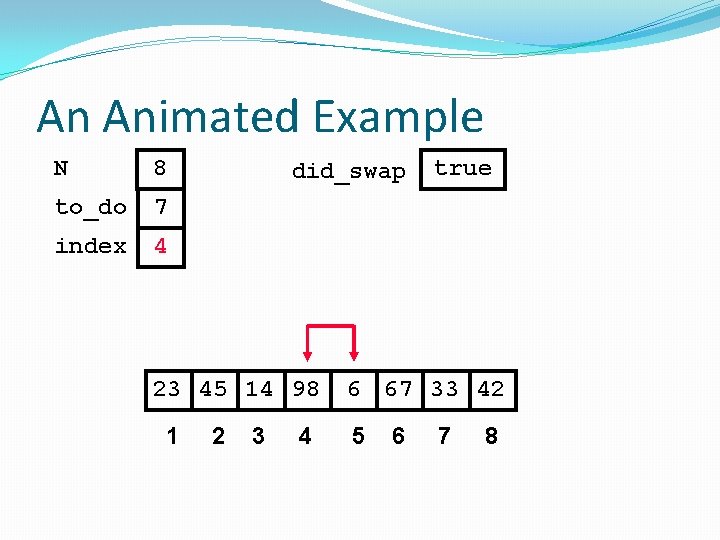
An Animated Example N 8 to_do 7 index 4 did_swap 23 45 14 98 1 2 3 4 true 6 67 33 42 5 6 7 8

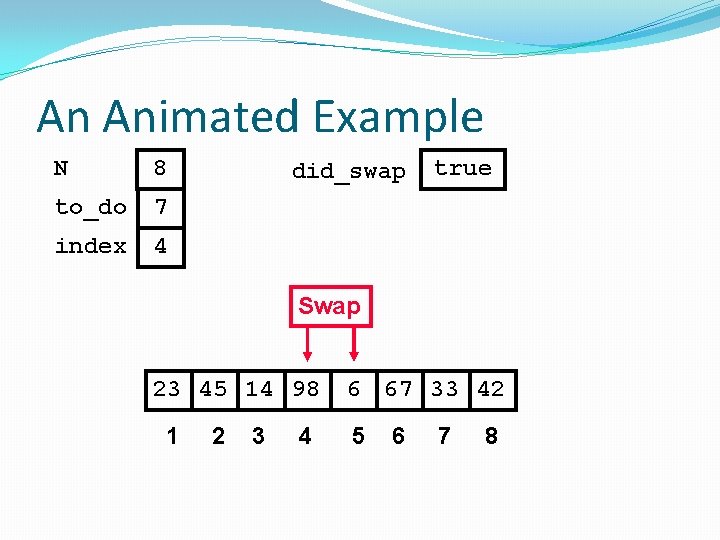
An Animated Example N 8 to_do 7 index 4 did_swap true Swap 23 45 14 98 1 2 3 4 6 67 33 42 5 6 7 8

An Animated Example N 8 to_do 7 index 4 did_swap true Swap 23 45 14 6 1 2 3 4 98 67 33 42 5 6 7 8

An Animated Example N 8 to_do 7 index 5 did_swap 23 45 14 6 1 2 3 4 true 98 67 33 42 5 6 7 8

An Animated Example N 8 to_do 7 index 5 did_swap true Swap 23 45 14 6 1 2 3 4 98 67 33 42 5 6 7 8

An Animated Example N 8 to_do 7 index 5 did_swap true Swap 23 45 14 6 1 2 3 4 67 98 33 42 5 6 7 8

An Animated Example N 8 to_do 7 index 6 did_swap 23 45 14 6 1 2 3 4 true 67 98 33 42 5 6 7 8

An Animated Example N 8 to_do 7 index 6 did_swap true Swap 23 45 14 6 1 2 3 4 67 98 33 42 5 6 7 8

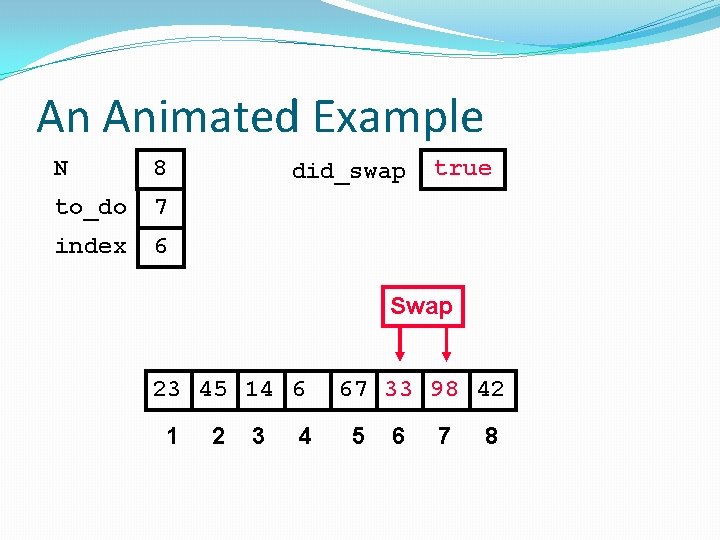
An Animated Example N 8 to_do 7 index 6 did_swap true Swap 23 45 14 6 1 2 3 4 67 33 98 42 5 6 7 8

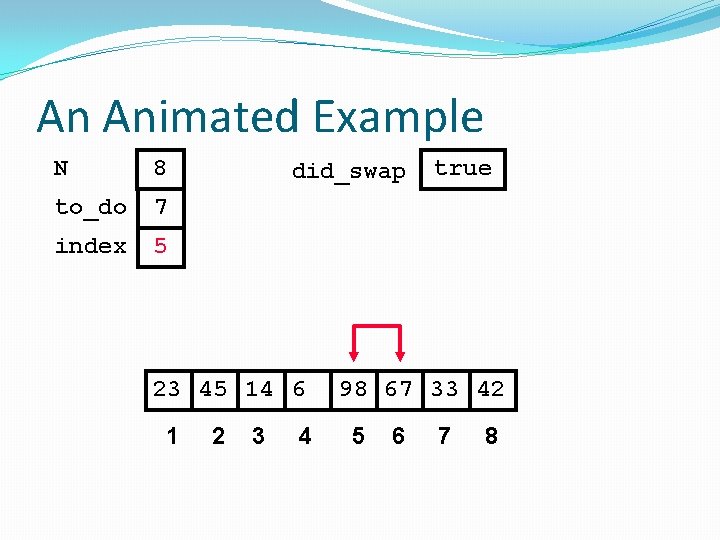
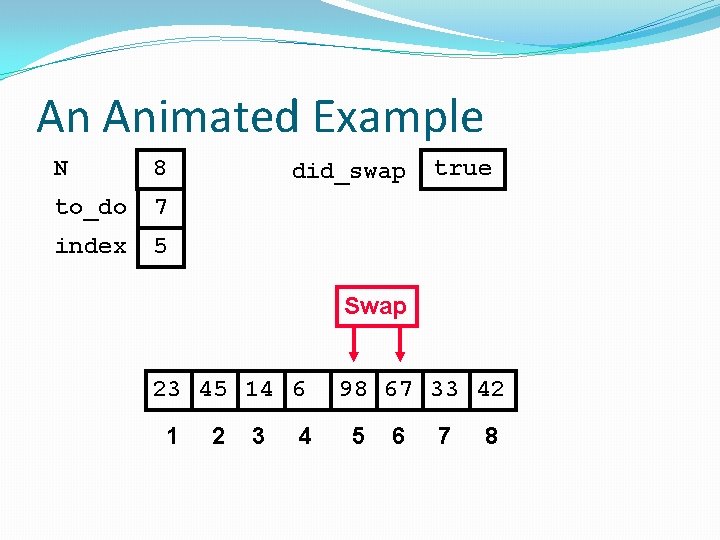
An Animated Example N 8 to_do 7 index 7 did_swap 23 45 14 6 1 2 3 4 true 67 33 98 42 5 6 7 8

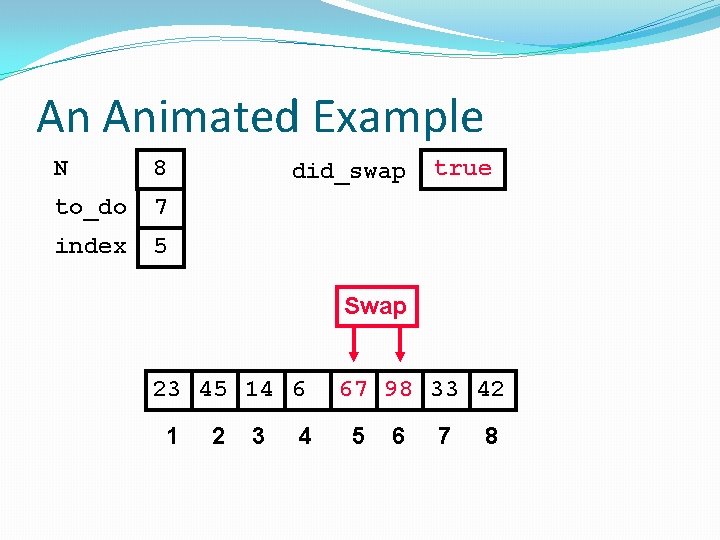
An Animated Example N 8 to_do 7 index 7 did_swap true Swap 23 45 14 6 1 2 3 4 67 33 98 42 5 6 7 8

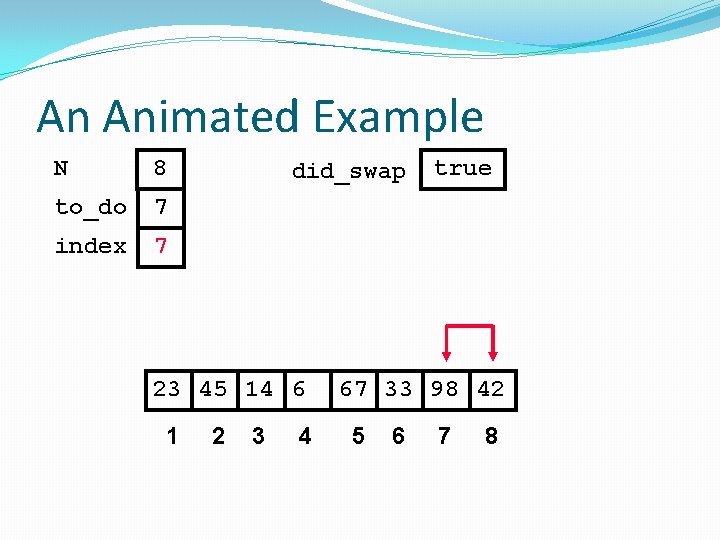
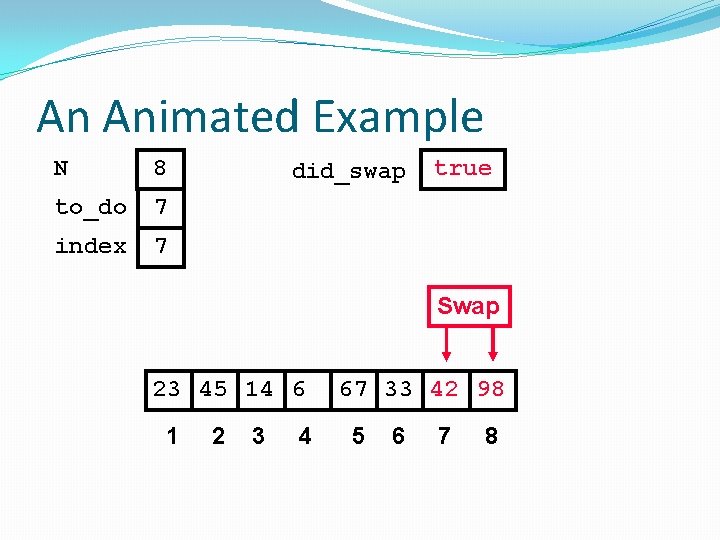
An Animated Example N 8 to_do 7 index 7 did_swap true Swap 23 45 14 6 1 2 3 4 67 33 42 98 5 6 7 8

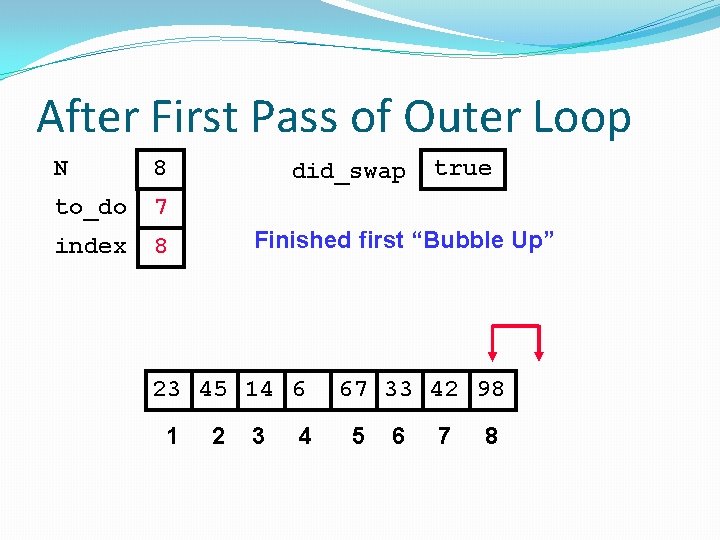
After First Pass of Outer Loop N 8 to_do 7 index 8 did_swap Finished first “Bubble Up” 23 45 14 6 1 true 2 3 4 67 33 42 98 5 6 7 8

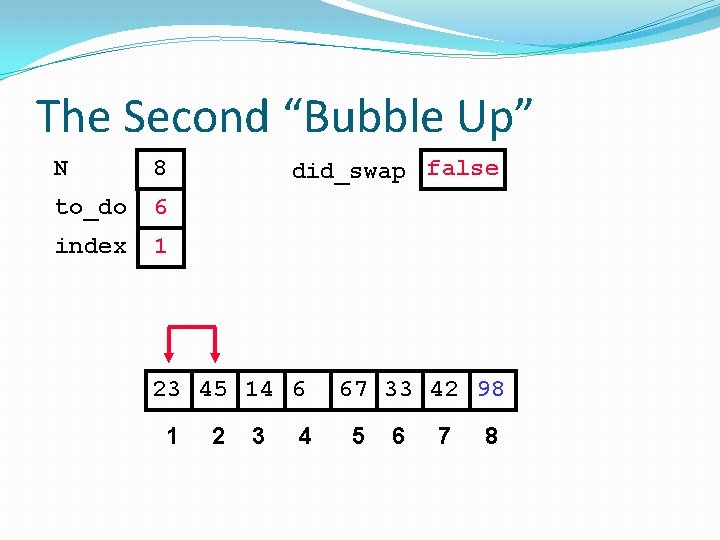
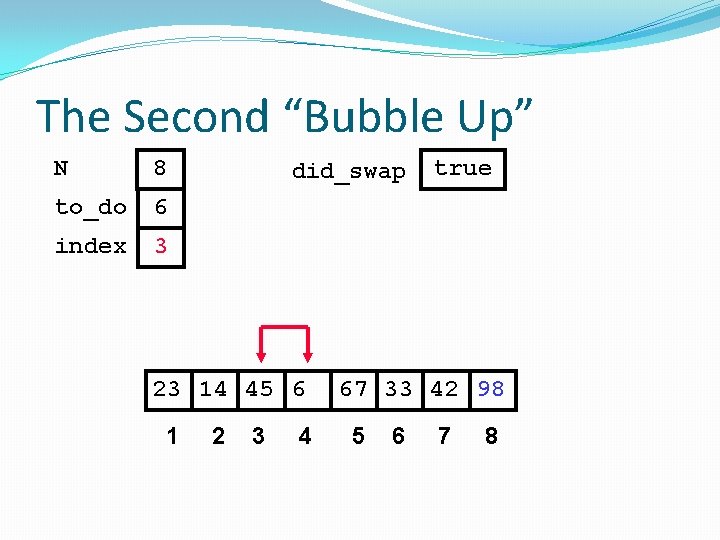
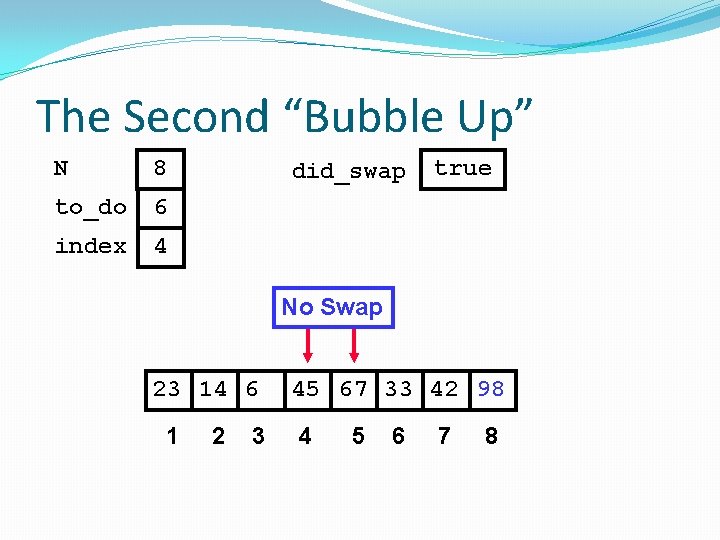
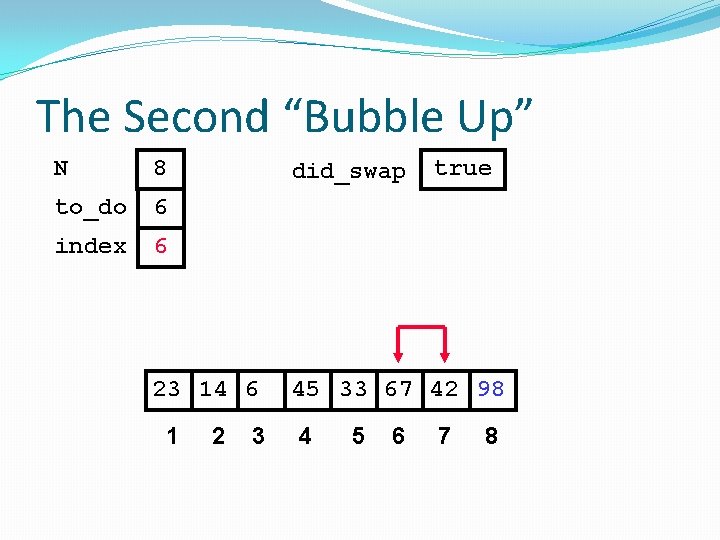
The Second “Bubble Up” N 8 to_do 6 index 1 did_swap false 23 45 14 6 1 2 3 4 67 33 42 98 5 6 7 8

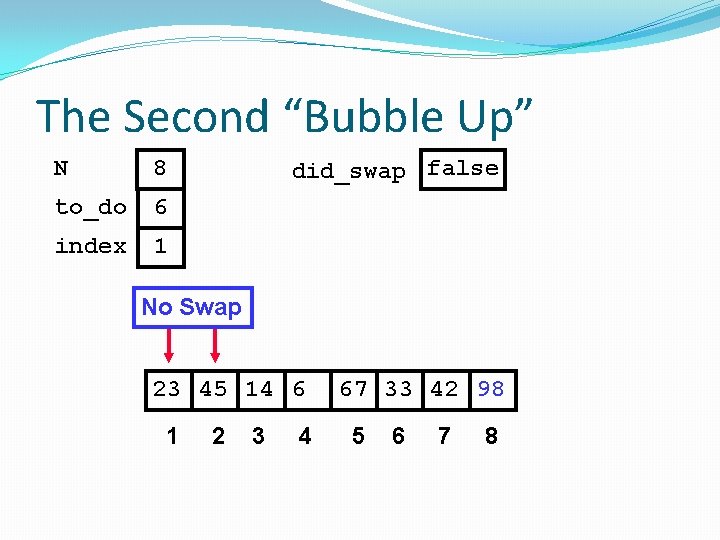
The Second “Bubble Up” N 8 to_do 6 index 1 did_swap false No Swap 23 45 14 6 1 2 3 4 67 33 42 98 5 6 7 8

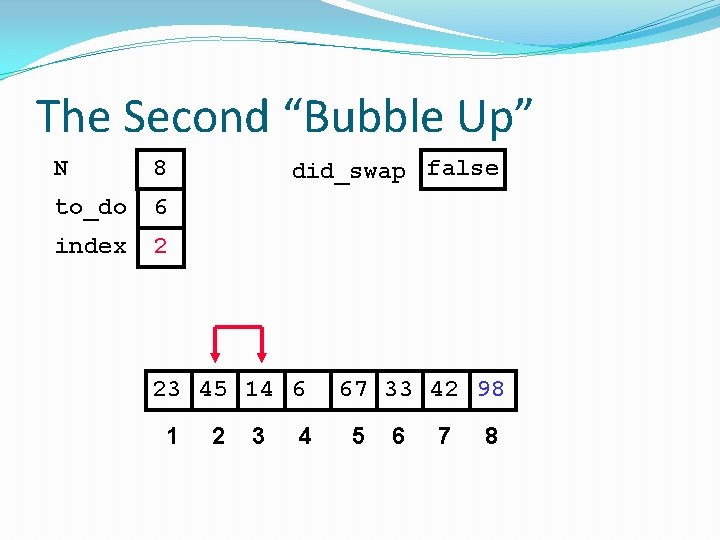
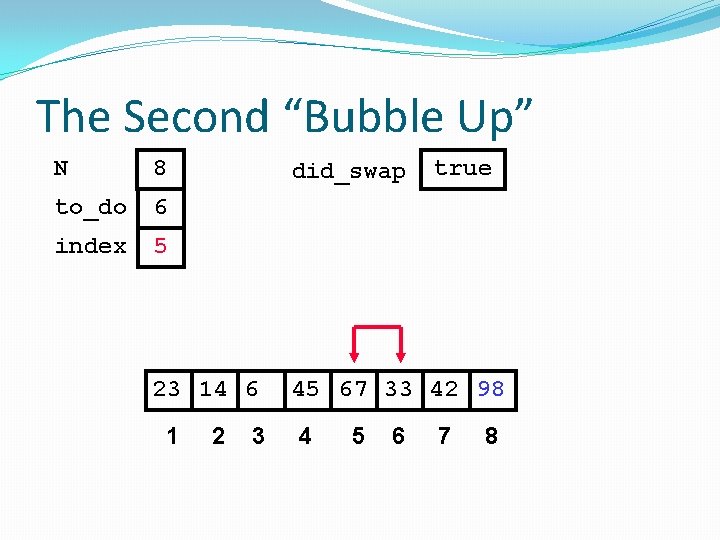
The Second “Bubble Up” N 8 to_do 6 index 2 did_swap false 23 45 14 6 1 2 3 4 67 33 42 98 5 6 7 8

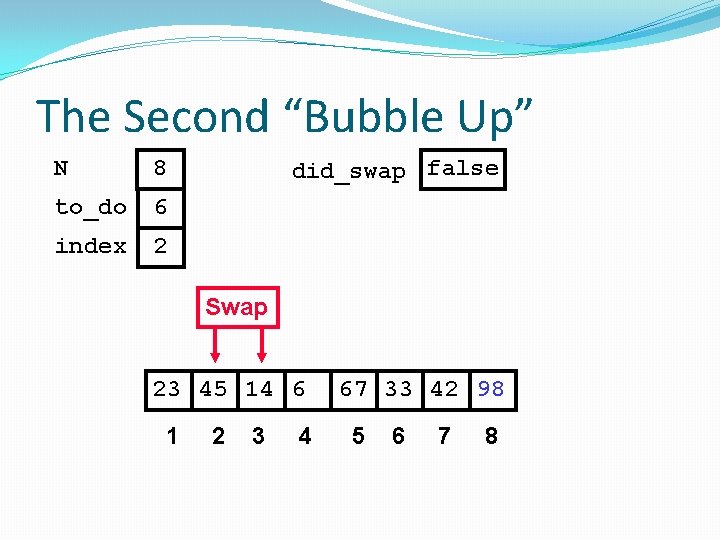
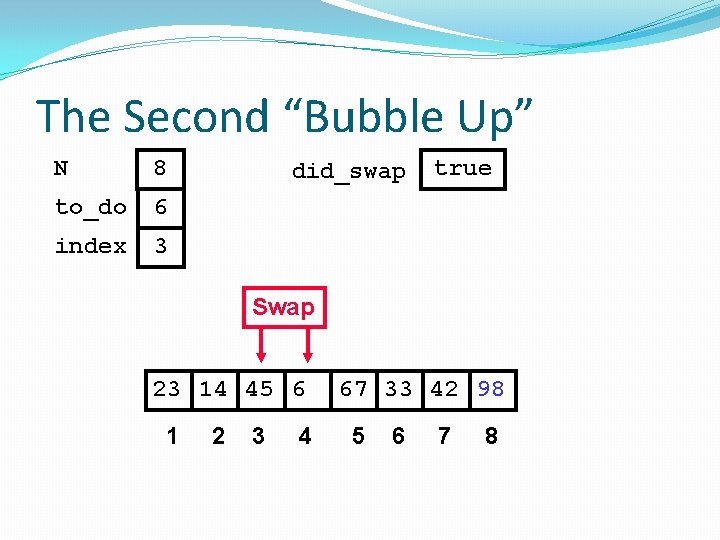
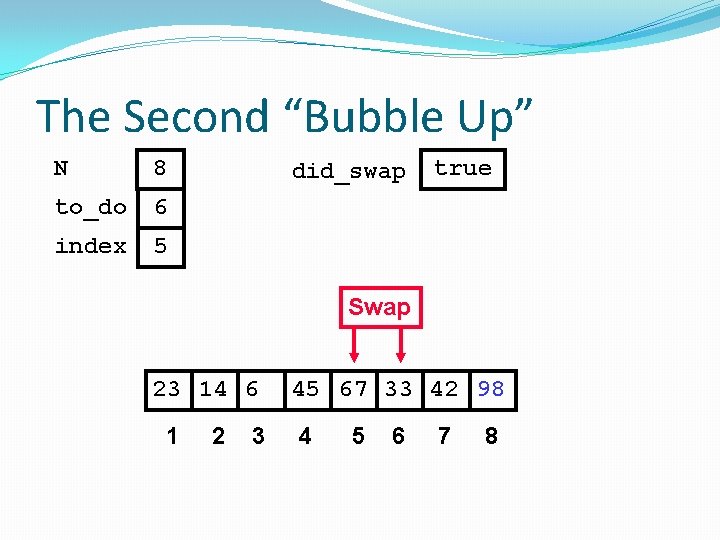
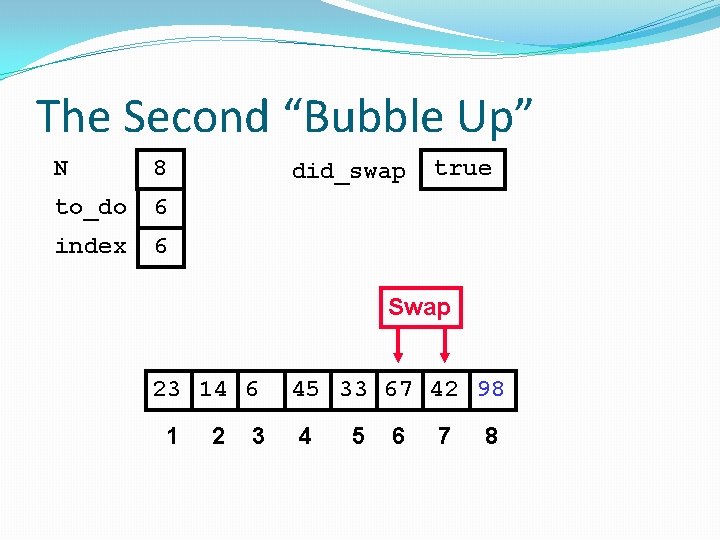
The Second “Bubble Up” N 8 to_do 6 index 2 did_swap false Swap 23 45 14 6 1 2 3 4 67 33 42 98 5 6 7 8

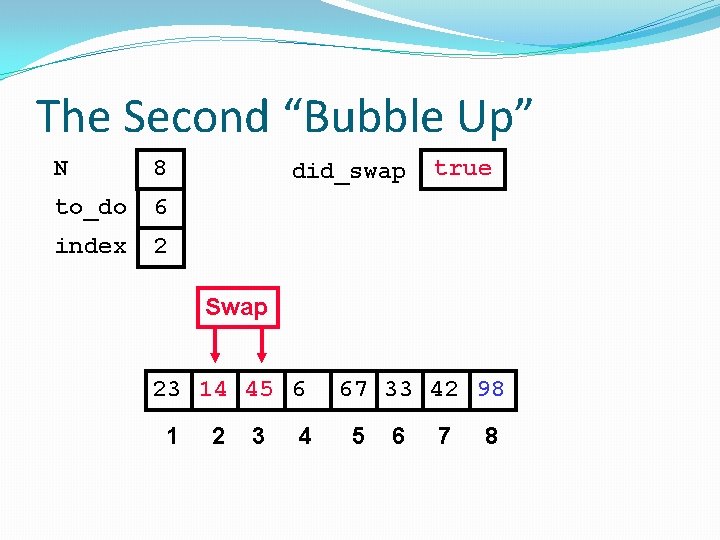
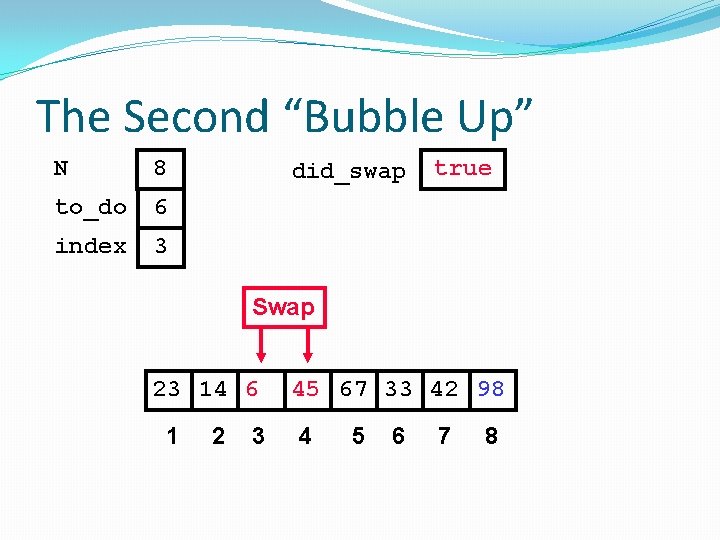
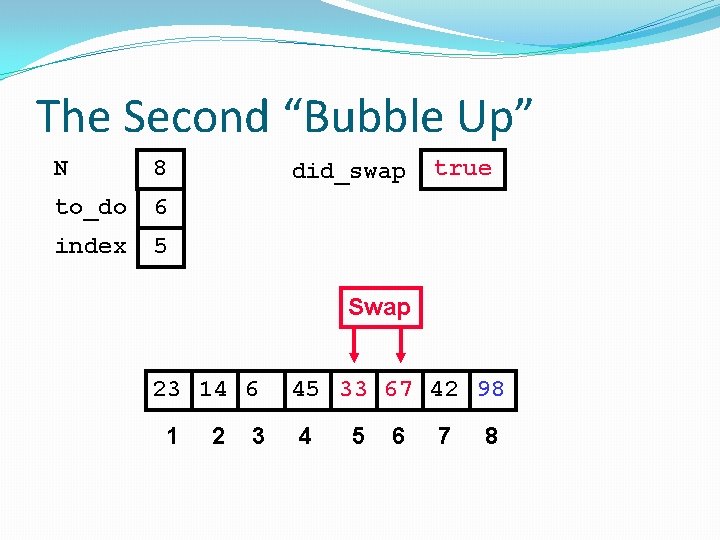
The Second “Bubble Up” N 8 to_do 6 index 2 did_swap true Swap 23 14 45 6 1 2 3 4 67 33 42 98 5 6 7 8

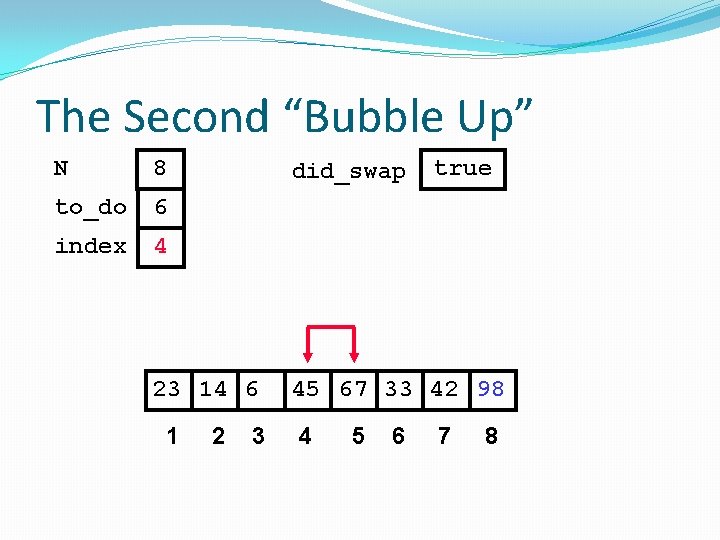
The Second “Bubble Up” N 8 to_do 6 index 3 did_swap 23 14 45 6 1 2 3 4 true 67 33 42 98 5 6 7 8

The Second “Bubble Up” N 8 to_do 6 index 3 did_swap true Swap 23 14 45 6 1 2 3 4 67 33 42 98 5 6 7 8

The Second “Bubble Up” N 8 to_do 6 index 3 did_swap true Swap 23 14 6 1 2 3 45 67 33 42 98 4 5 6 7 8

The Second “Bubble Up” N 8 to_do 6 index 4 did_swap 23 14 6 1 2 3 true 45 67 33 42 98 4 5 6 7 8

The Second “Bubble Up” N 8 to_do 6 index 4 did_swap true No Swap 23 14 6 1 2 3 45 67 33 42 98 4 5 6 7 8

The Second “Bubble Up” N 8 to_do 6 index 5 did_swap 23 14 6 1 2 3 true 45 67 33 42 98 4 5 6 7 8

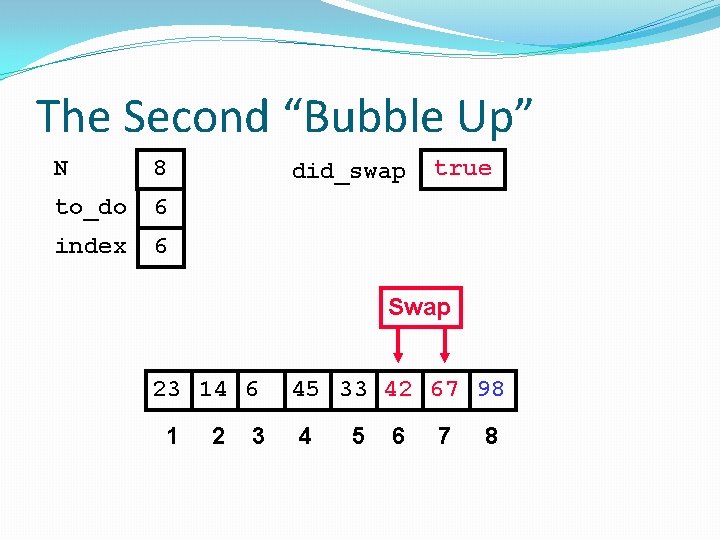
The Second “Bubble Up” N 8 to_do 6 index 5 did_swap true Swap 23 14 6 1 2 3 45 67 33 42 98 4 5 6 7 8

The Second “Bubble Up” N 8 to_do 6 index 5 did_swap true Swap 23 14 6 1 2 3 45 33 67 42 98 4 5 6 7 8

The Second “Bubble Up” N 8 to_do 6 index 6 did_swap 23 14 6 1 2 3 true 45 33 67 42 98 4 5 6 7 8

The Second “Bubble Up” N 8 to_do 6 index 6 did_swap true Swap 23 14 6 1 2 3 45 33 67 42 98 4 5 6 7 8

The Second “Bubble Up” N 8 to_do 6 index 6 did_swap true Swap 23 14 6 1 2 3 45 33 42 67 98 4 5 6 7 8

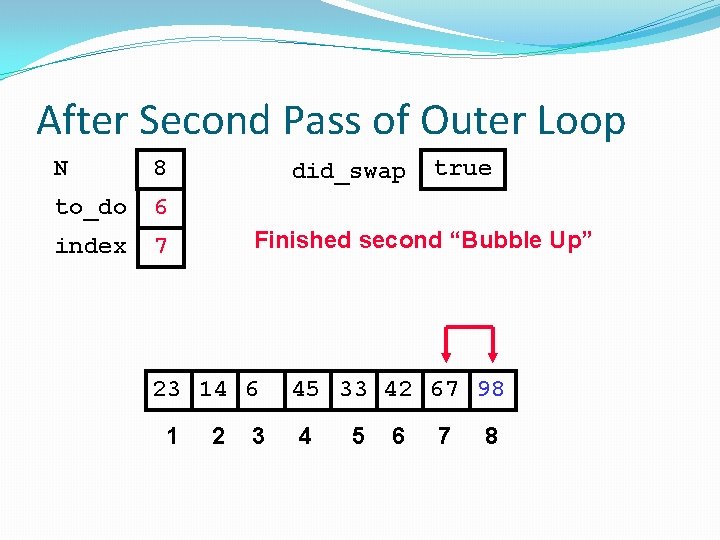
After Second Pass of Outer Loop N 8 to_do 6 index 7 did_swap Finished second “Bubble Up” 23 14 6 1 true 2 3 45 33 42 67 98 4 5 6 7 8

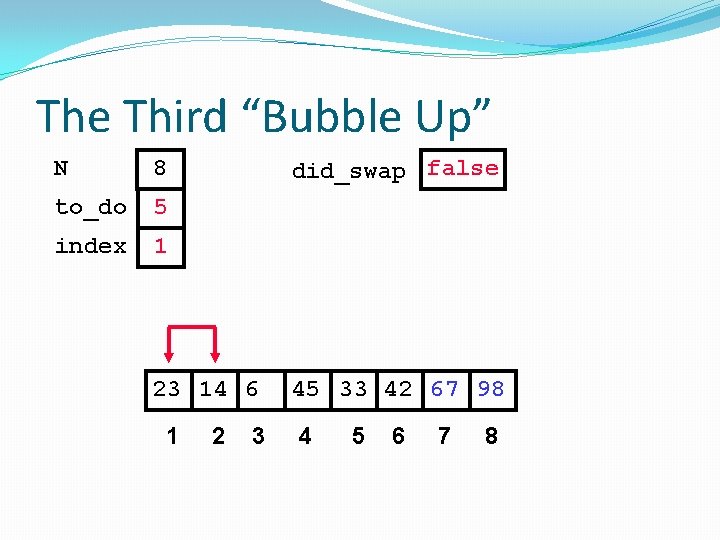
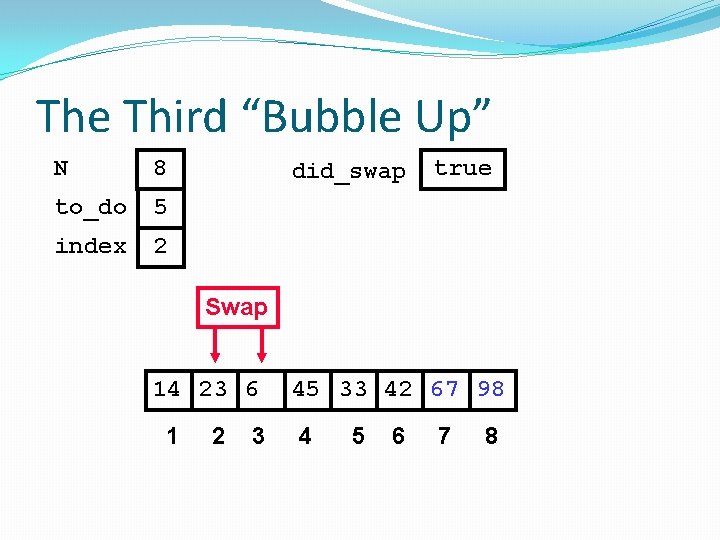
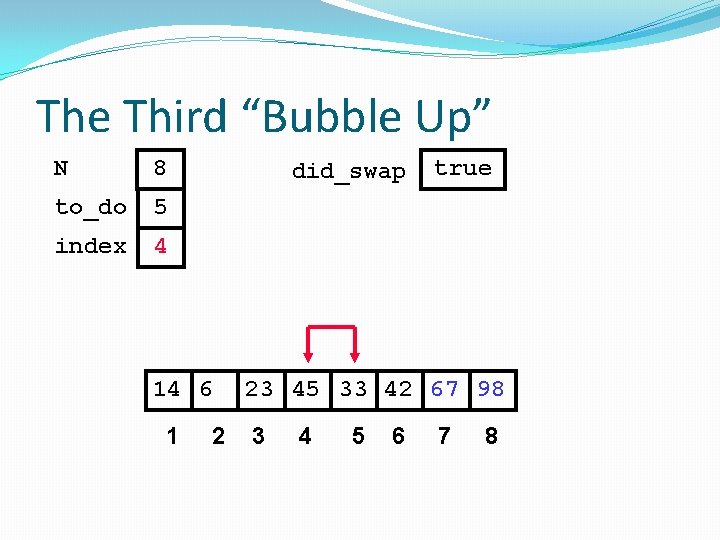
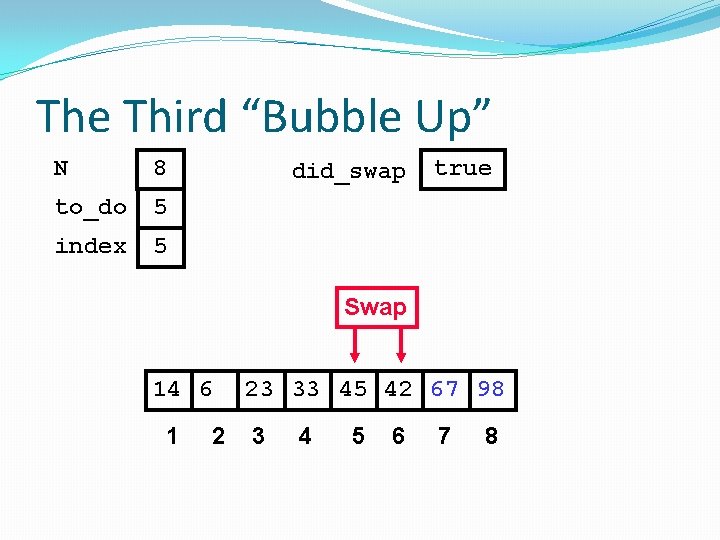
The Third “Bubble Up” N 8 to_do 5 index 1 did_swap false 23 14 6 1 2 3 45 33 42 67 98 4 5 6 7 8

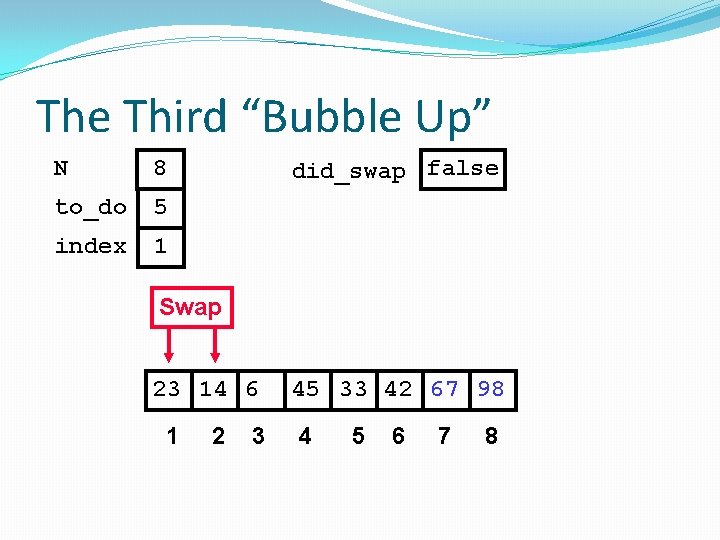
The Third “Bubble Up” N 8 to_do 5 index 1 did_swap false Swap 23 14 6 1 2 3 45 33 42 67 98 4 5 6 7 8

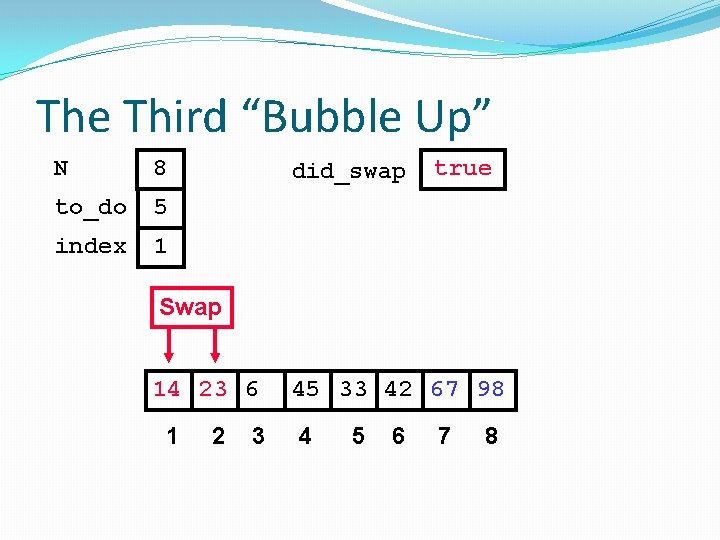
The Third “Bubble Up” N 8 to_do 5 index 1 did_swap true Swap 14 23 6 1 2 3 45 33 42 67 98 4 5 6 7 8

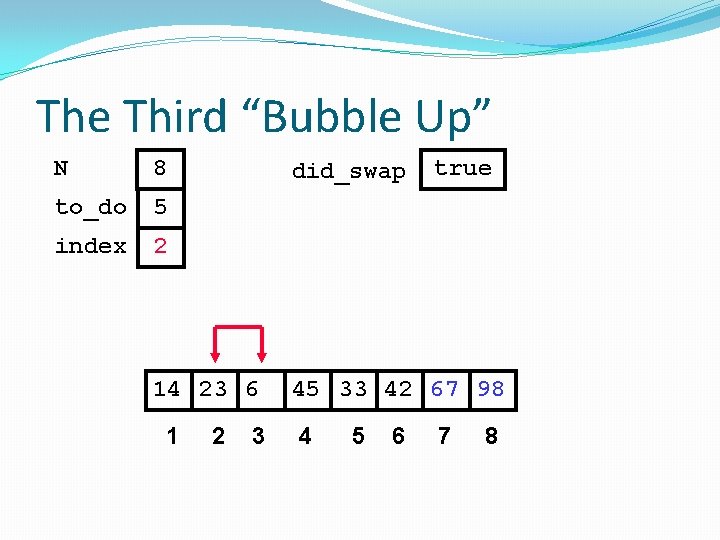
The Third “Bubble Up” N 8 to_do 5 index 2 did_swap 14 23 6 1 2 3 true 45 33 42 67 98 4 5 6 7 8

The Third “Bubble Up” N 8 to_do 5 index 2 did_swap true Swap 14 23 6 1 2 3 45 33 42 67 98 4 5 6 7 8

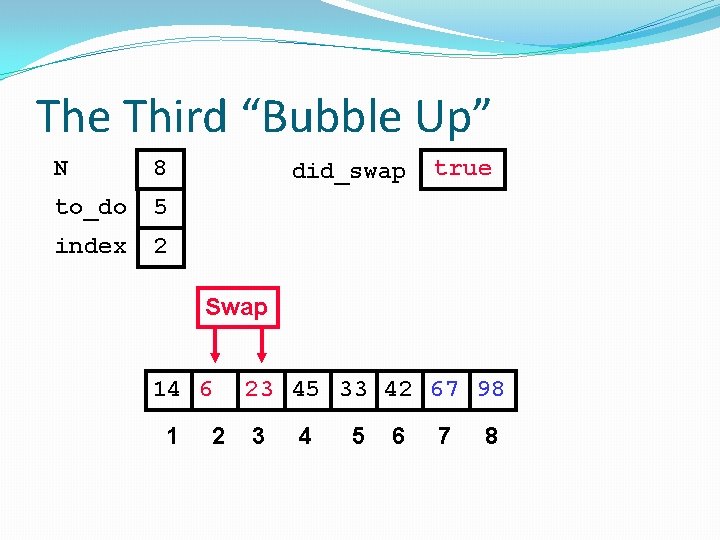
The Third “Bubble Up” N 8 to_do 5 index 2 did_swap true Swap 14 6 1 2 23 45 33 42 67 98 3 4 5 6 7 8

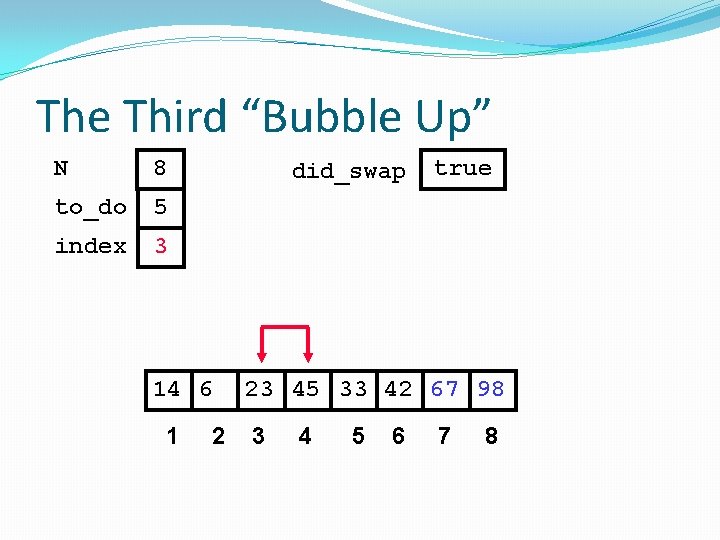
The Third “Bubble Up” N 8 to_do 5 index 3 did_swap 14 6 1 2 true 23 45 33 42 67 98 3 4 5 6 7 8

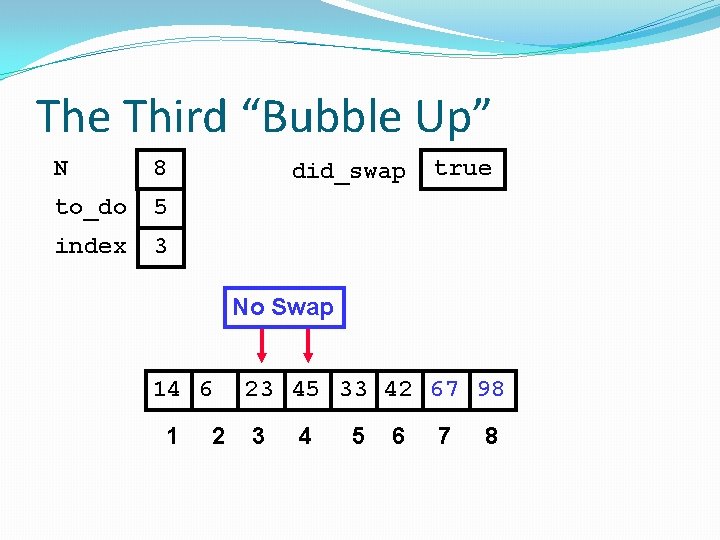
The Third “Bubble Up” N 8 to_do 5 index 3 did_swap true No Swap 14 6 1 2 23 45 33 42 67 98 3 4 5 6 7 8

The Third “Bubble Up” N 8 to_do 5 index 4 did_swap 14 6 1 2 true 23 45 33 42 67 98 3 4 5 6 7 8

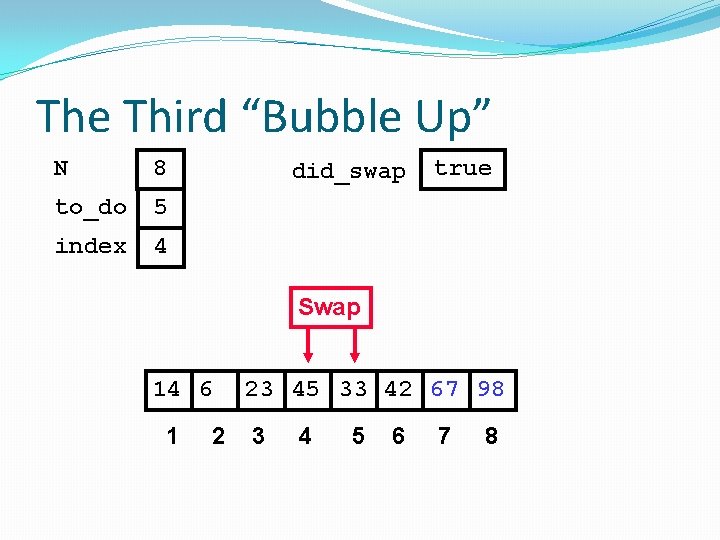
The Third “Bubble Up” N 8 to_do 5 index 4 did_swap true Swap 14 6 1 2 23 45 33 42 67 98 3 4 5 6 7 8

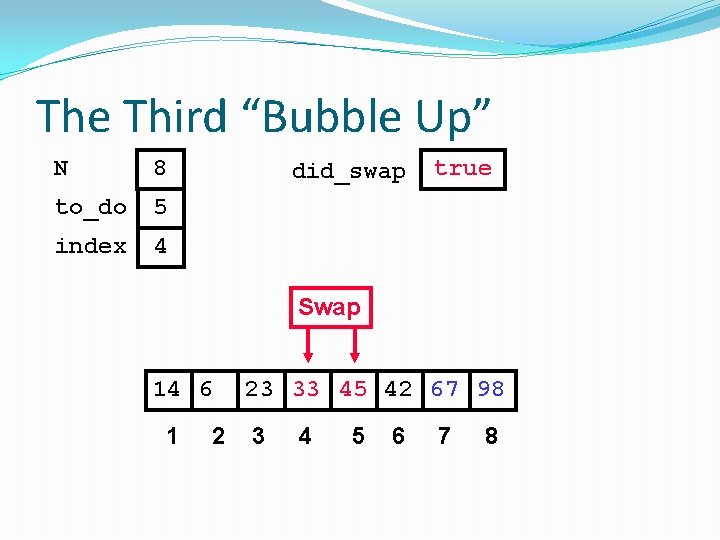
The Third “Bubble Up” N 8 to_do 5 index 4 did_swap true Swap 14 6 1 2 23 33 45 42 67 98 3 4 5 6 7 8

The Third “Bubble Up” N 8 to_do 5 index 5 did_swap 14 6 1 2 true 23 33 45 42 67 98 3 4 5 6 7 8

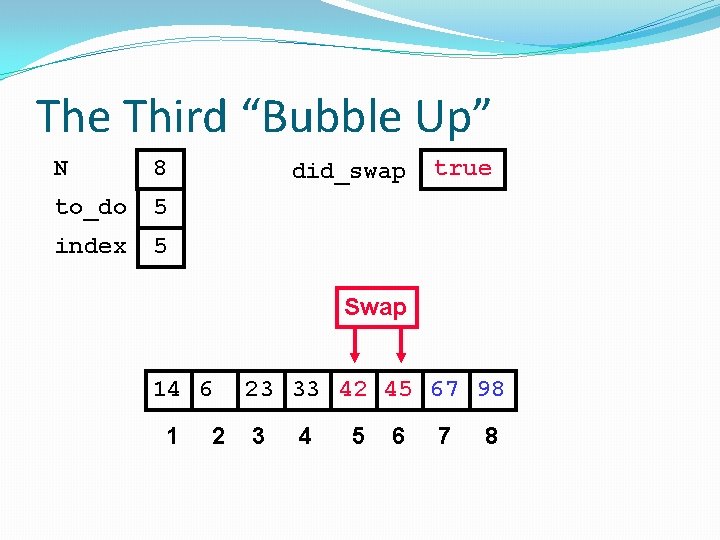
The Third “Bubble Up” N 8 to_do 5 index 5 did_swap true Swap 14 6 1 2 23 33 45 42 67 98 3 4 5 6 7 8

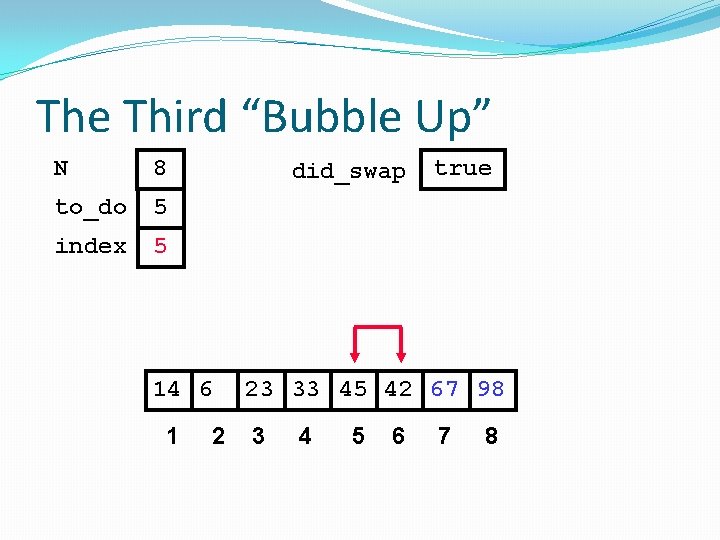
The Third “Bubble Up” N 8 to_do 5 index 5 did_swap true Swap 14 6 1 2 23 33 42 45 67 98 3 4 5 6 7 8

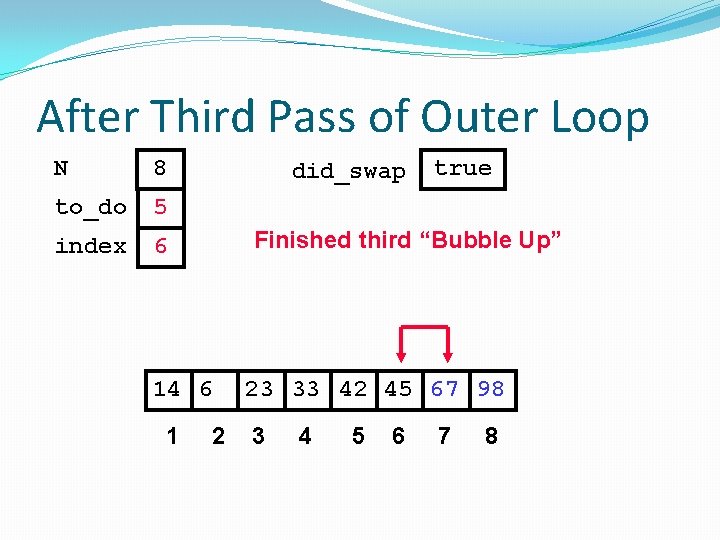
After Third Pass of Outer Loop N 8 to_do 5 index 6 did_swap Finished third “Bubble Up” 14 6 1 true 2 23 33 42 45 67 98 3 4 5 6 7 8

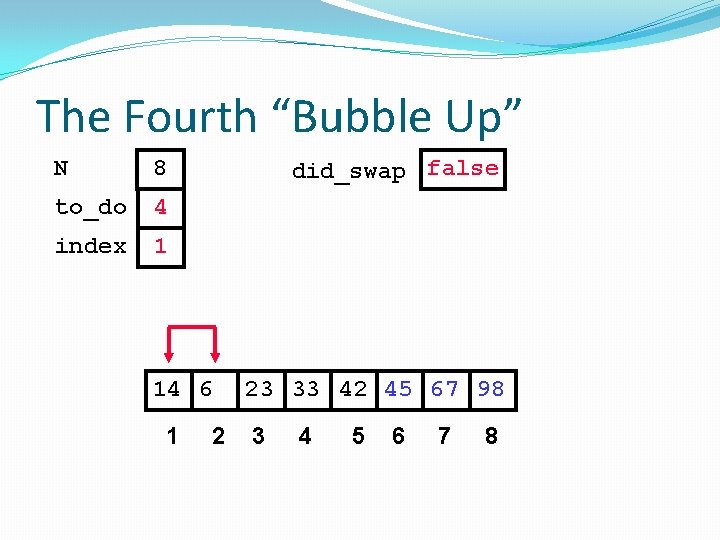
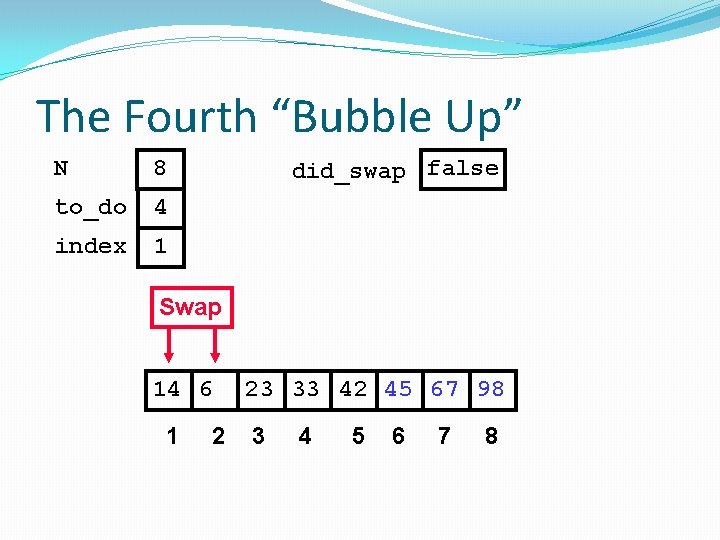
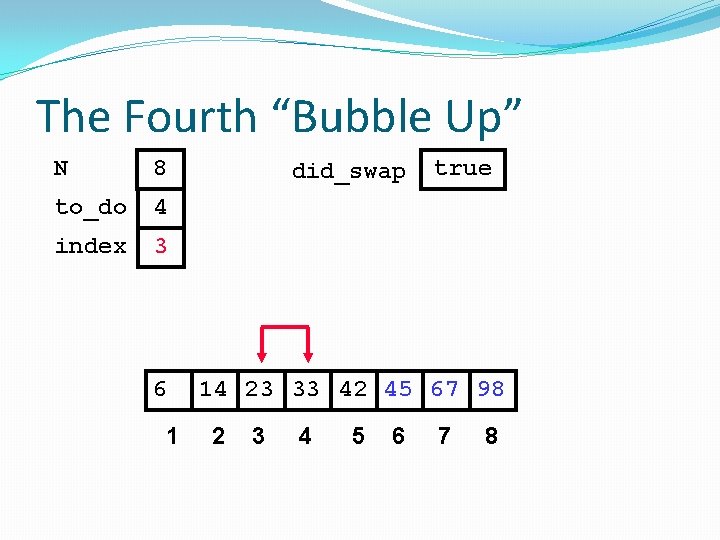
The Fourth “Bubble Up” N 8 to_do 4 index 1 did_swap false 14 6 1 2 23 33 42 45 67 98 3 4 5 6 7 8

The Fourth “Bubble Up” N 8 to_do 4 index 1 did_swap false Swap 14 6 1 2 23 33 42 45 67 98 3 4 5 6 7 8

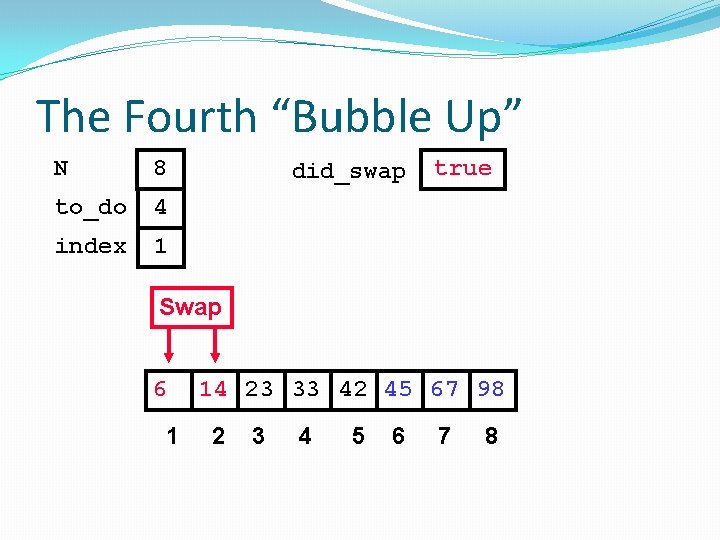
The Fourth “Bubble Up” N 8 to_do 4 index 1 did_swap true Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

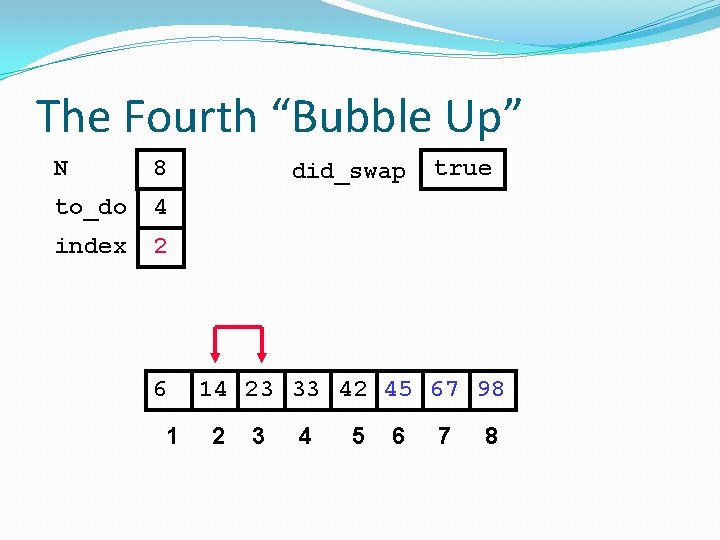
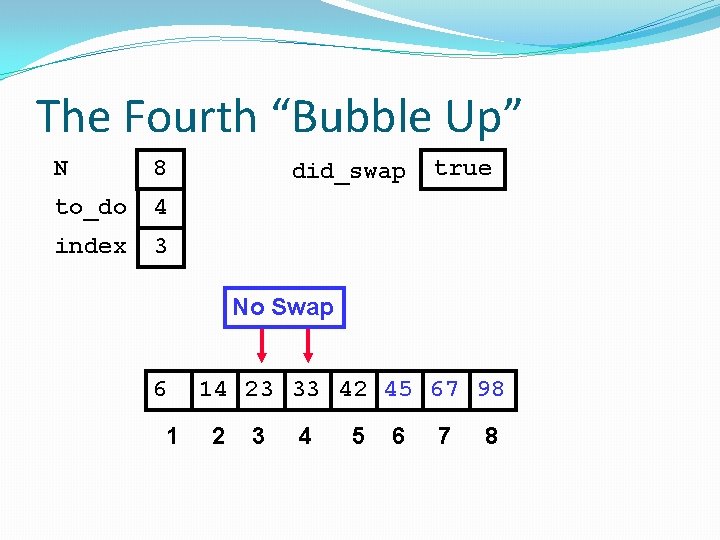
The Fourth “Bubble Up” N 8 to_do 4 index 2 6 1 did_swap true 14 23 33 42 45 67 98 2 3 4 5 6 7 8

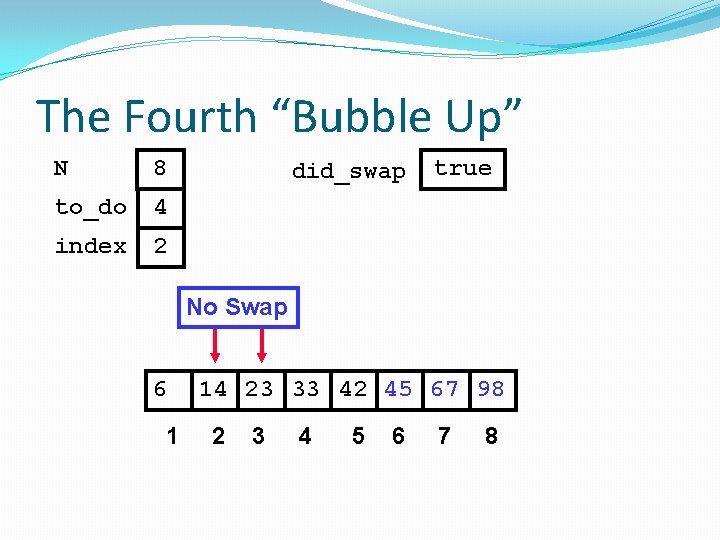
The Fourth “Bubble Up” N 8 to_do 4 index 2 did_swap true No Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

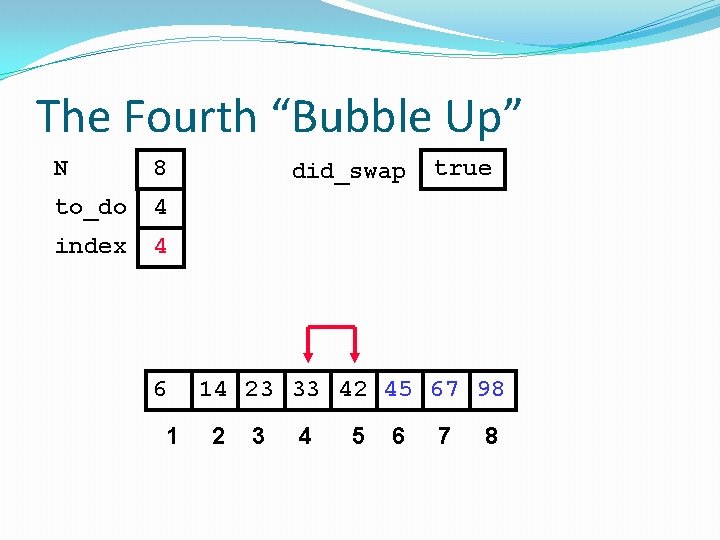
The Fourth “Bubble Up” N 8 to_do 4 index 3 6 1 did_swap true 14 23 33 42 45 67 98 2 3 4 5 6 7 8

The Fourth “Bubble Up” N 8 to_do 4 index 3 did_swap true No Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

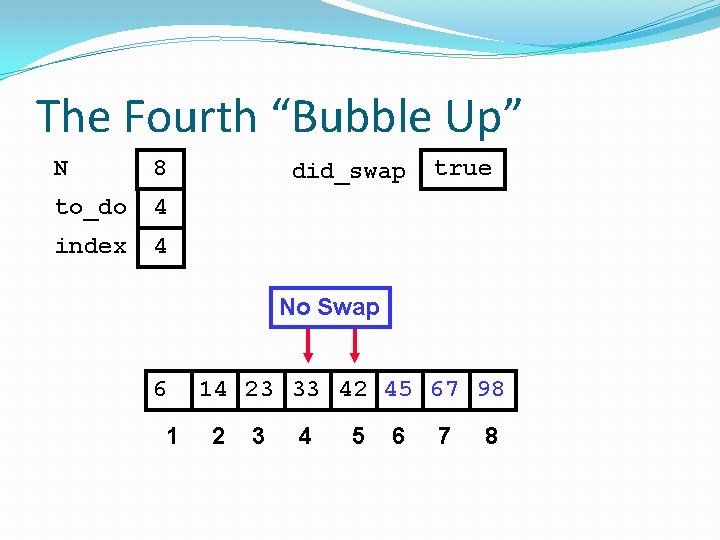
The Fourth “Bubble Up” N 8 to_do 4 index 4 6 1 did_swap true 14 23 33 42 45 67 98 2 3 4 5 6 7 8

The Fourth “Bubble Up” N 8 to_do 4 index 4 did_swap true No Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

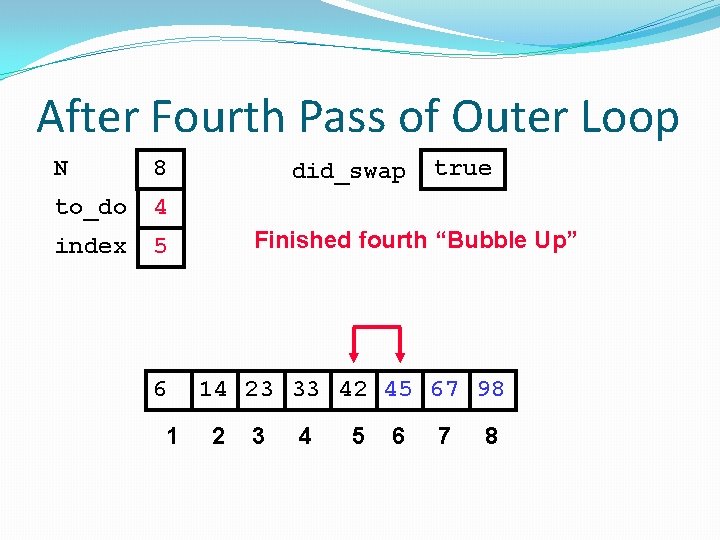
After Fourth Pass of Outer Loop N 8 to_do 4 index 5 6 1 did_swap true Finished fourth “Bubble Up” 14 23 33 42 45 67 98 2 3 4 5 6 7 8

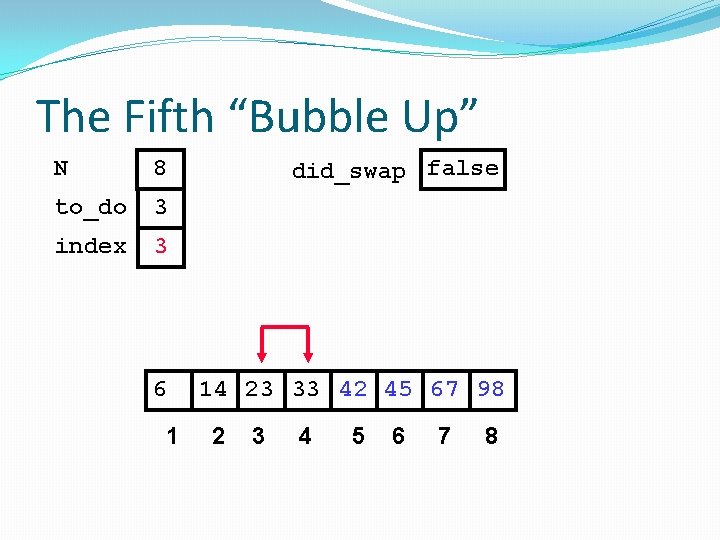
The Fifth “Bubble Up” N 8 to_do 3 index 1 6 1 did_swap false 14 23 33 42 45 67 98 2 3 4 5 6 7 8

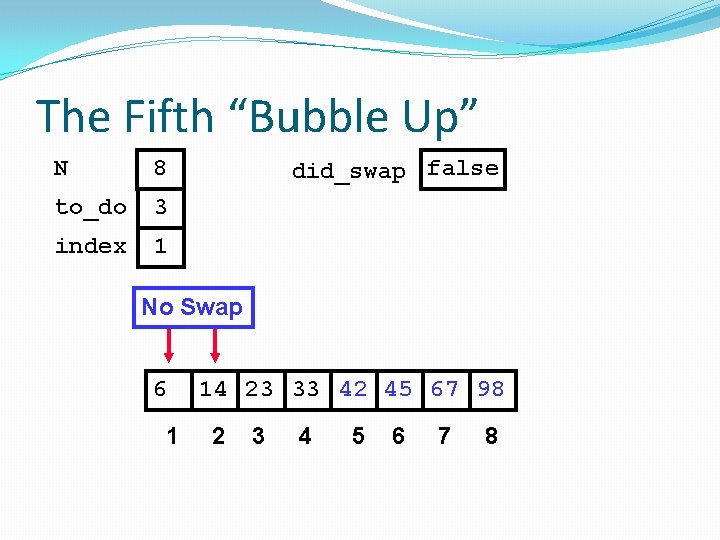
The Fifth “Bubble Up” N 8 to_do 3 index 1 did_swap false No Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

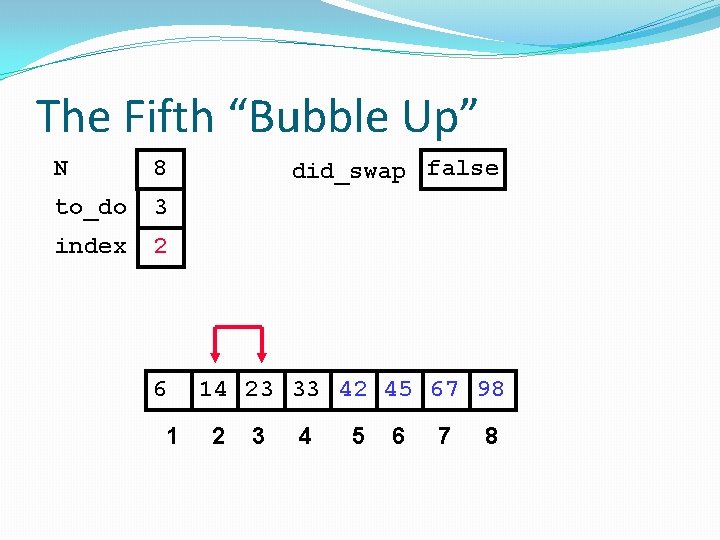
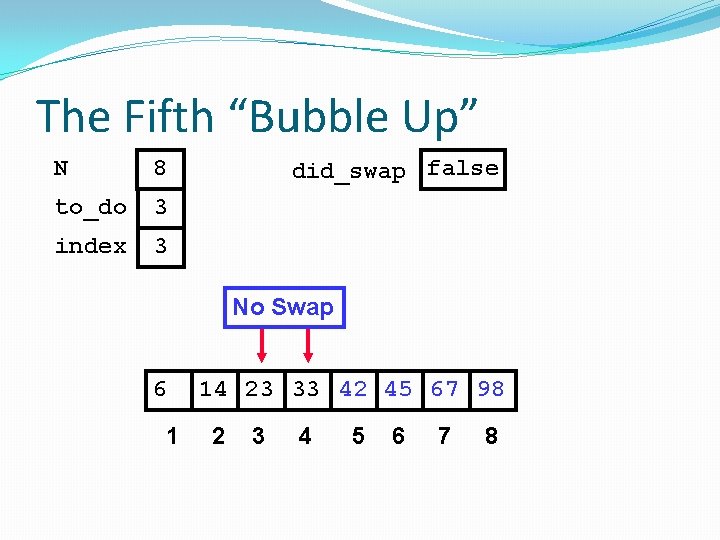
The Fifth “Bubble Up” N 8 to_do 3 index 2 6 1 did_swap false 14 23 33 42 45 67 98 2 3 4 5 6 7 8

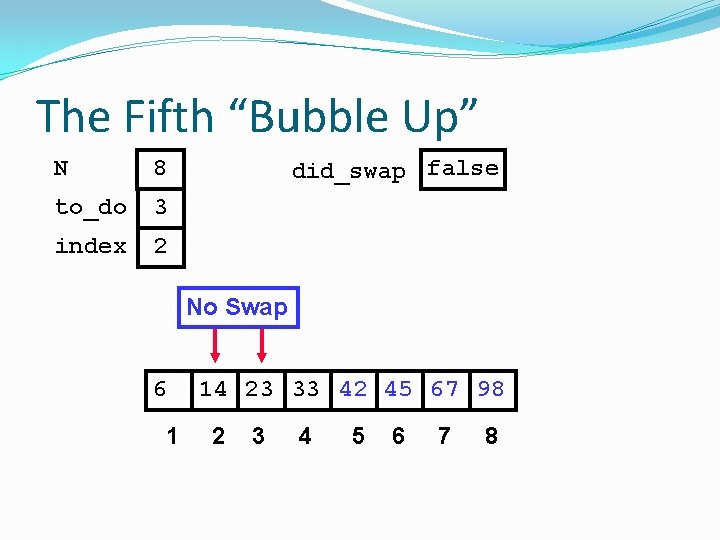
The Fifth “Bubble Up” N 8 to_do 3 index 2 did_swap false No Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

The Fifth “Bubble Up” N 8 to_do 3 index 3 6 1 did_swap false 14 23 33 42 45 67 98 2 3 4 5 6 7 8

The Fifth “Bubble Up” N 8 to_do 3 index 3 did_swap false No Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

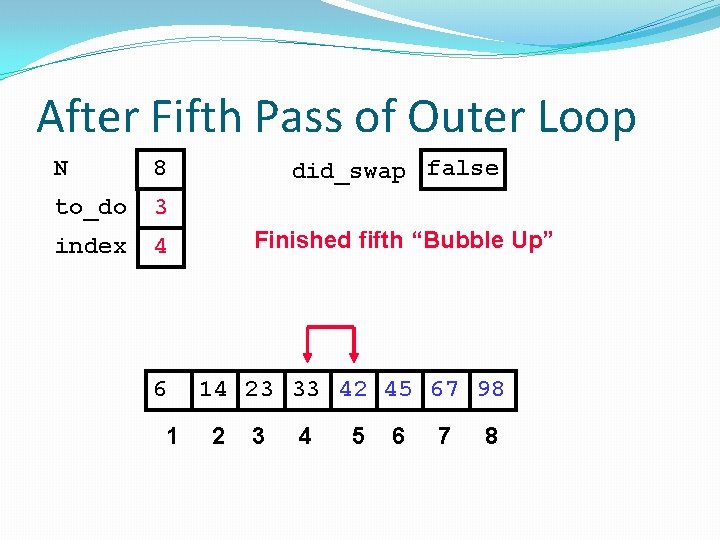
After Fifth Pass of Outer Loop N 8 to_do 3 index 4 6 1 did_swap false Finished fifth “Bubble Up” 14 23 33 42 45 67 98 2 3 4 5 6 7 8

Finished “Early” N 8 to_do 3 index 4 did_swap false We didn’t do any swapping, so all of the other elements must be correctly placed. We can “skip” the last two passes of the outer loop. 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

Time Complexity �Best Case n � Average Case n 2 �Worst Case n 2

Insertion Sort

Insertion Sort �while some elements unsorted: �Using linear search, find the location in the sorted portion where the 1 st element of the unsorted portion should be inserted �Move all the elements after the insertion location up one position to make space for the new element

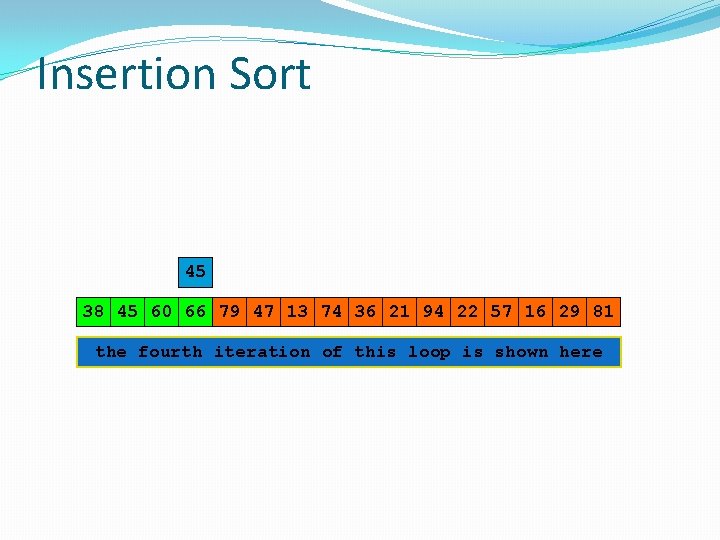
Insertion Sort 45 38 45 60 60 66 45 66 79 47 13 74 36 21 94 22 57 16 29 81 the fourth iteration of this loop is shown here

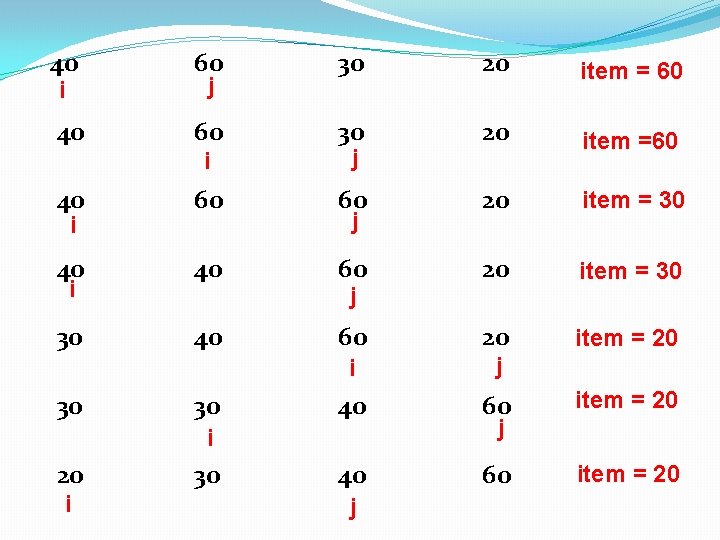
40 60 30 20 item = 60 40 60 30 i j 20 item =60 40 60 60 20 item = 30 40 40 60 20 item = 30 30 40 60 20 item = 20 i j 40 60 item = 20 i i i 30 j j i 20 i 30 j j

Pseudo-code Procedure_Insertion sort(a, n) start 1. Loop: j=1 To n 1. 2. 3. item=a[j] i=j-1 while((i>=0)&& (item<a[i]) 1. 2. 3. 4. a[i+1]=a[i] i=i-1 End while loop a[i+1]=item 2. Loop End Exit

Time complexity �Best case: n – Linear �Average Case n 2 �Worst case n(n+1)/2 n 2 - Quadratic

Selection Sort

At start min=a[0]=40 40 60 30 20 min= 30 40 60 30 20 min = 20 60 30 40 min = 60 i j i 20 i j j 20 60 30 40 min = 30 20 30 60 40 min = 60 i j 60 40 min = 40 60 min = 40 20 i 30 j i 20 30 40 i j j

Pseudo-code Procedure_selection sort(a, n) start 1. Loop: i=0 To n-1 min =i; Loop: j=1 To n 1. 2. 3. If a[min]>a[j] Then min=j Inner loop of j End if a[i]>a[min] then 3. 1. Swap(a[i], a[min]) 2. Outer Loop of I End Exit

Time Complexity_ Selection �Best Case n 2 �Average Case n 2 �Worst Case n 2

Mergesort

Divide and Conquer �Divide and Conquer cuts the problem in half each time, but uses the result of both halves: �cut the problem in half until the problem is trivial �solve for both halves �combine the solutions

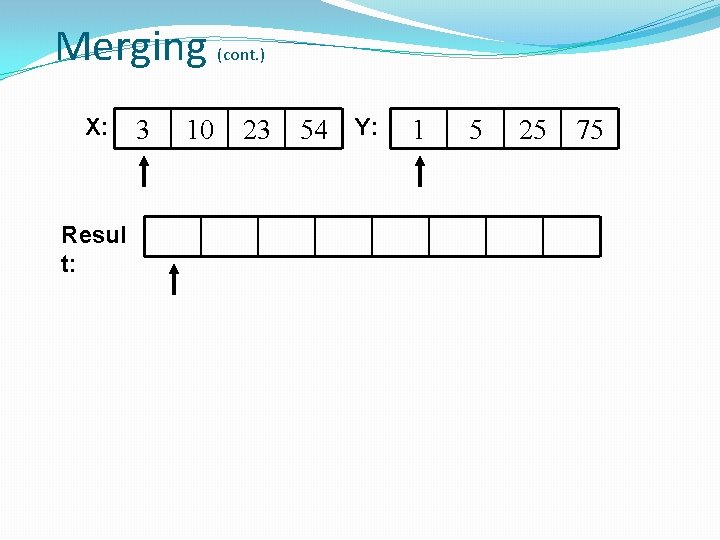
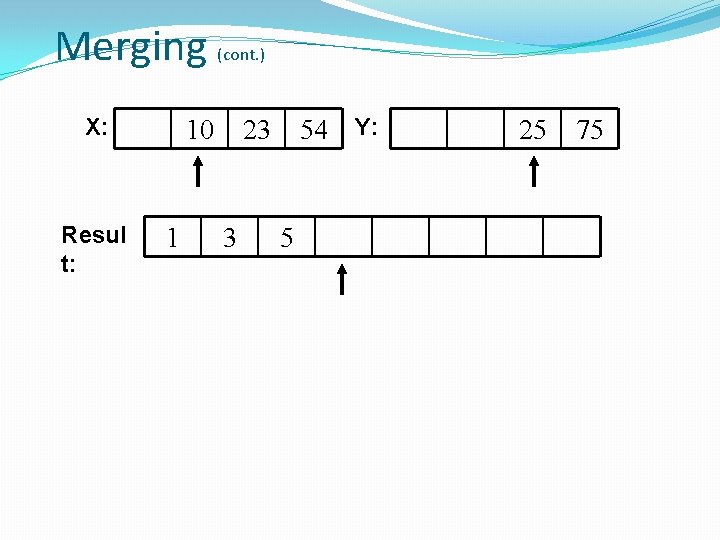
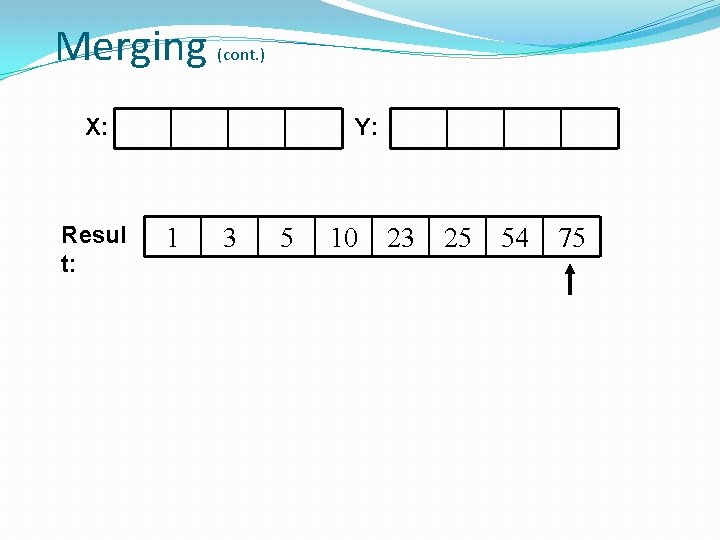
Merging �The key to Merge Sort is merging two sorted lists into one, such that if you have two lists �X (x 1 x 2 … xm) and Y(y 1 y 2 … yn) the resulting list is Z(z 1 z 2 … zm+n) �Example: L 1 = { 3 8 9 } L 2 = { 1 5 7 } merge(L 1, L 2) = { 1 3 5 7 8 9 }………………Donald E. Knuth (page 160).

Merging X: Resul t: 3 10 (cont. ) 23 54 Y: 1 5 25 75

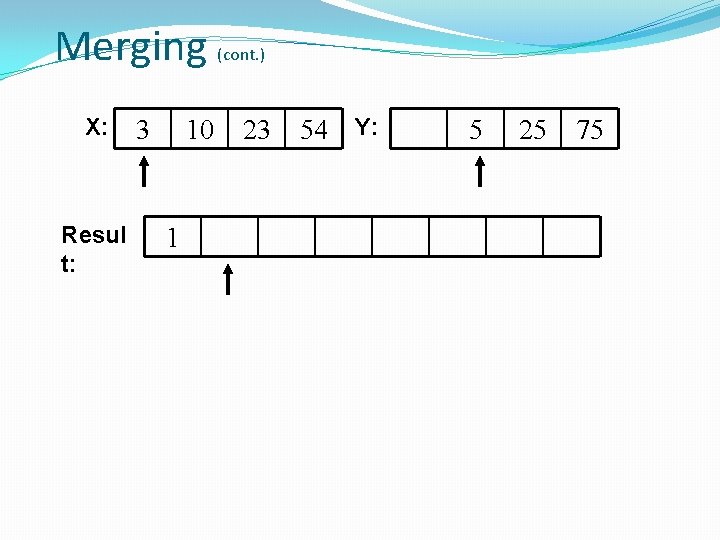
Merging X: Resul t: 3 10 1 (cont. ) 23 54 Y: 5 25 75

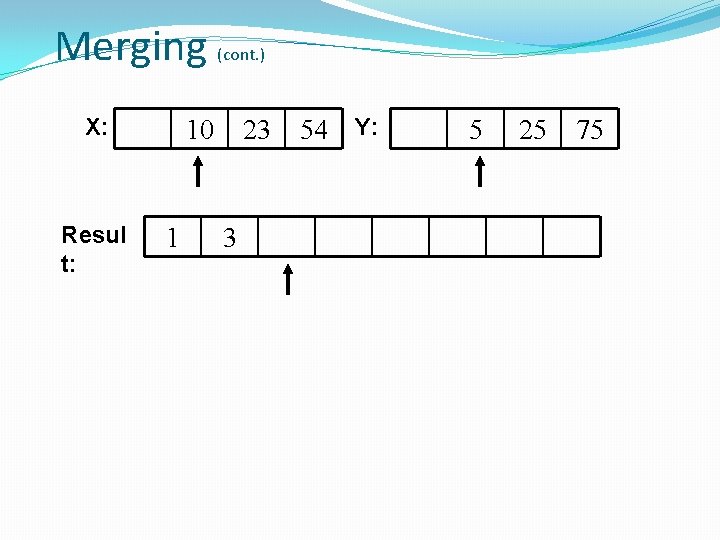
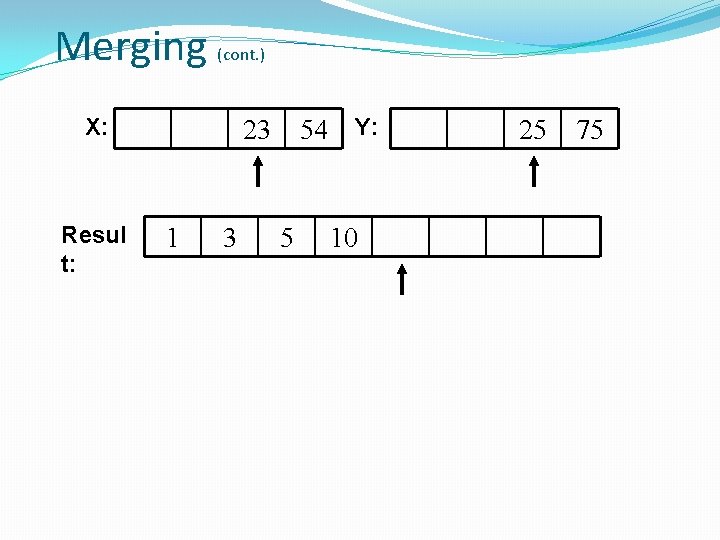
Merging X: Resul t: (cont. ) 10 1 23 3 54 Y: 5 25 75

Merging X: Resul t: (cont. ) 10 1 54 Y: 23 3 5 25 75

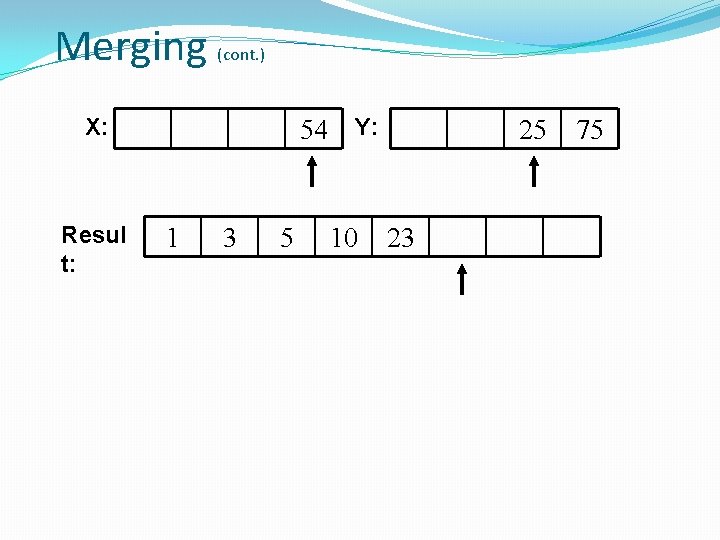
Merging (cont. ) X: Resul t: 54 Y: 23 1 3 5 10 25 75

Merging (cont. ) X: Resul t: 54 Y: 1 3 5 10 25 23 75

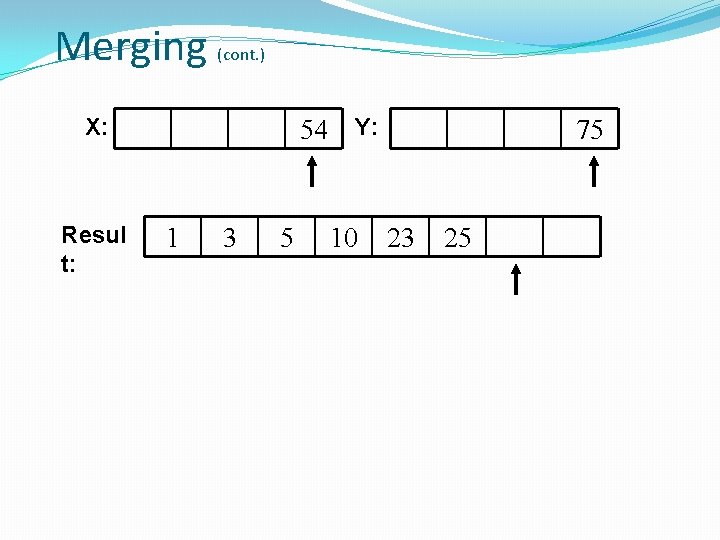
Merging (cont. ) X: Resul t: 54 Y: 1 3 5 10 75 23 25

Merging (cont. ) X: Resul t: Y: 1 3 5 10 75 23 25 54

Merging (cont. ) X: Resul t: Y: 1 3 5 10 23 25 54 75

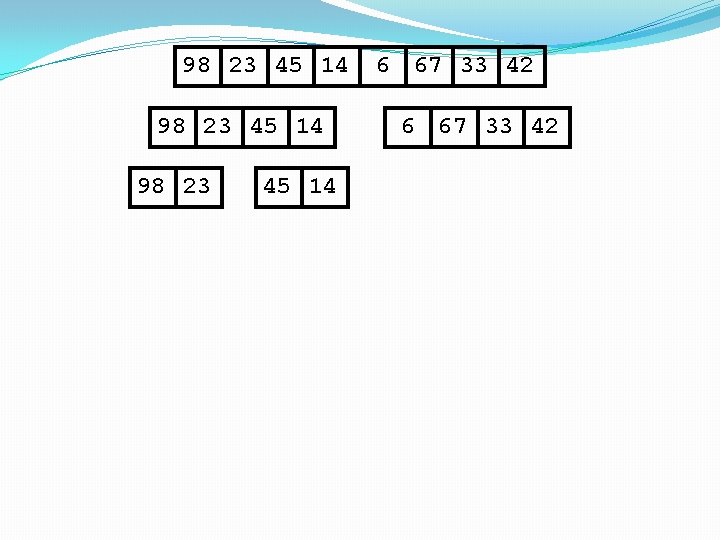
Merge sort -A divide-and-conquer algorithm: �Divide the unsorted array into 2 halves until the sub-arrays only contain one element �Merge the sub-problem solutions together: �Compare the sub-array’s first elements �Remove the smallest element and put it into the result array �Continue the process until all elements have been put into the result array

98 23 45 14 6 67 33 42

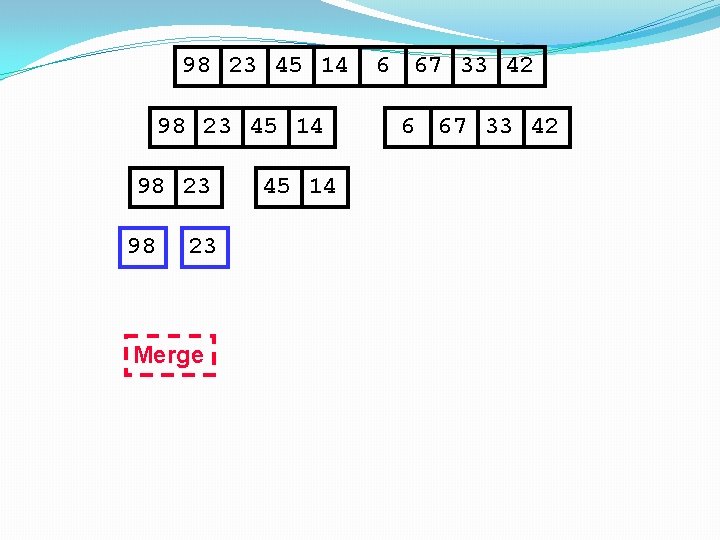
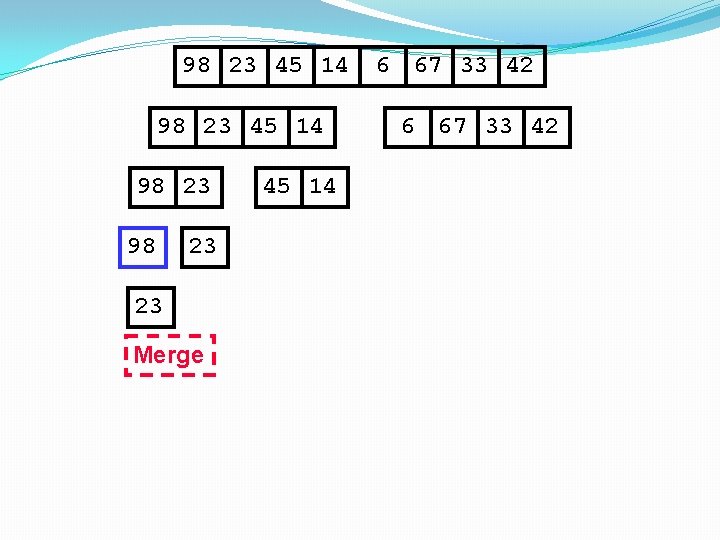
98 23 45 14 98 23 Merge 45 14 6 67 33 42

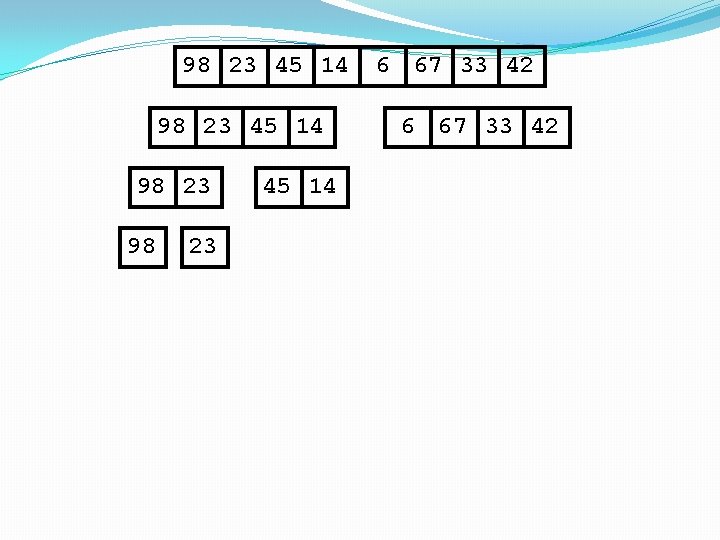
98 23 45 14 98 23 23 Merge 45 14 6 67 33 42

98 23 45 14 98 23 23 98 Merge 45 14 6 67 33 42

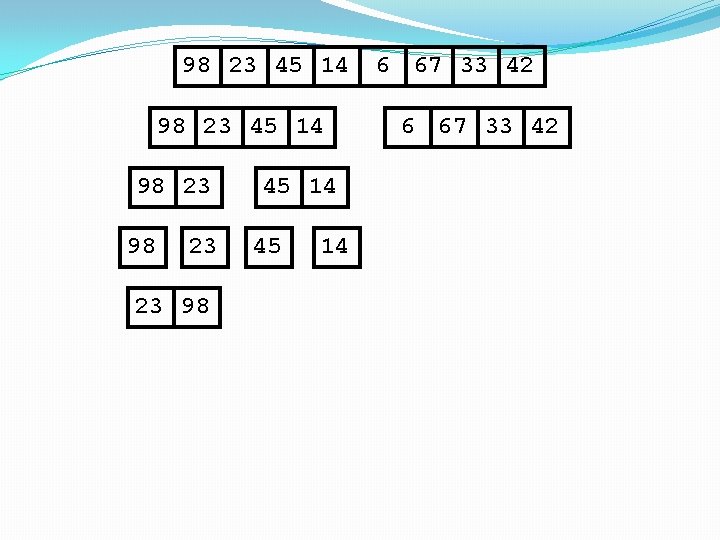
98 23 45 14 98 23 23 98 45 14 6 67 33 42

98 23 45 14 23 98 Merge 6 67 33 42

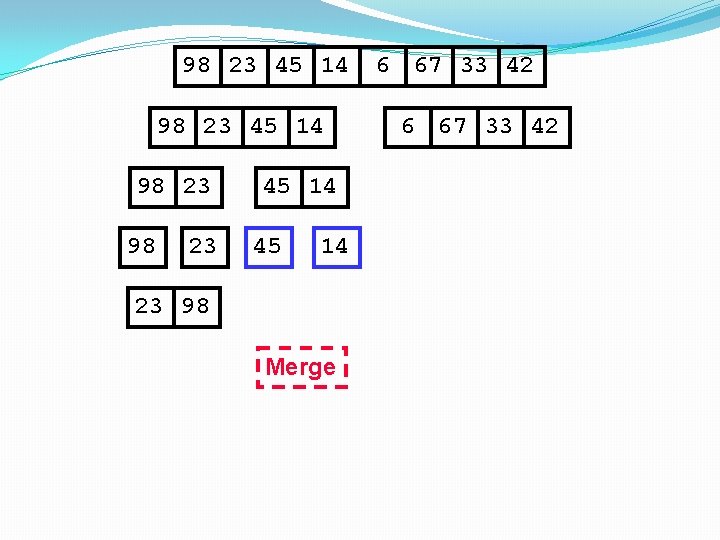
98 23 45 14 98 23 23 98 45 14 14 Merge 6 67 33 42

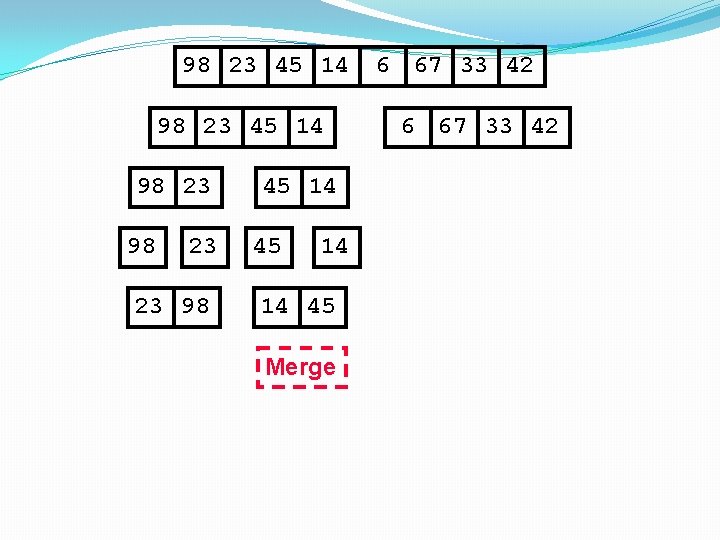
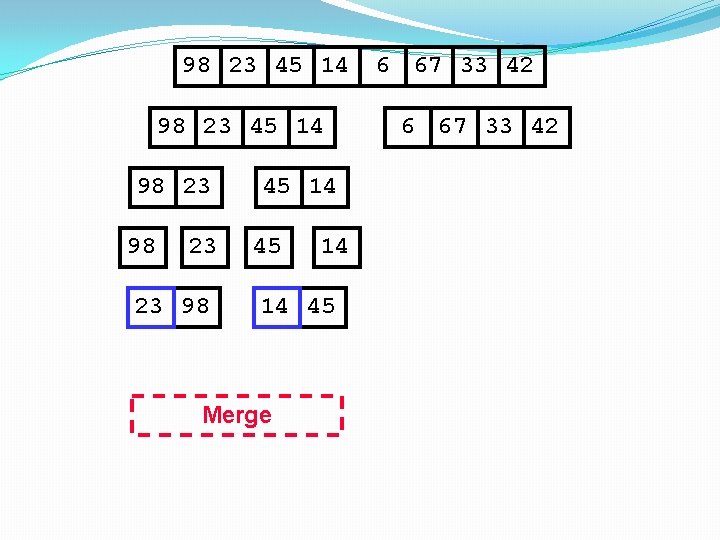
98 23 45 14 98 23 23 98 45 14 14 45 Merge 6 67 33 42

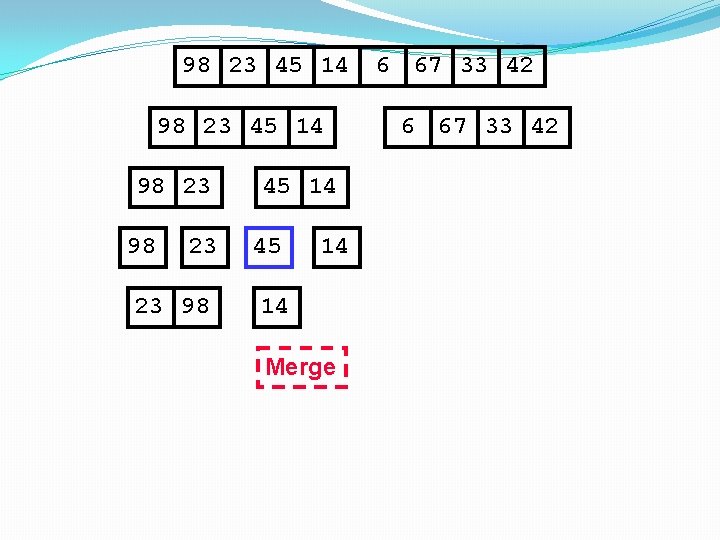
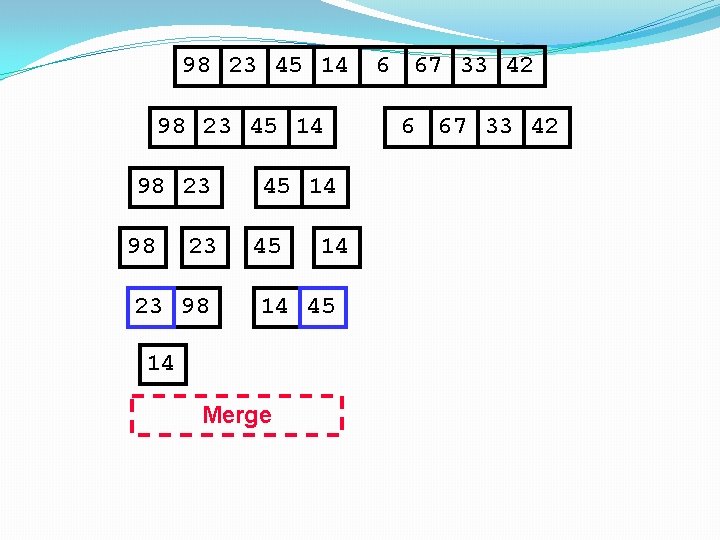
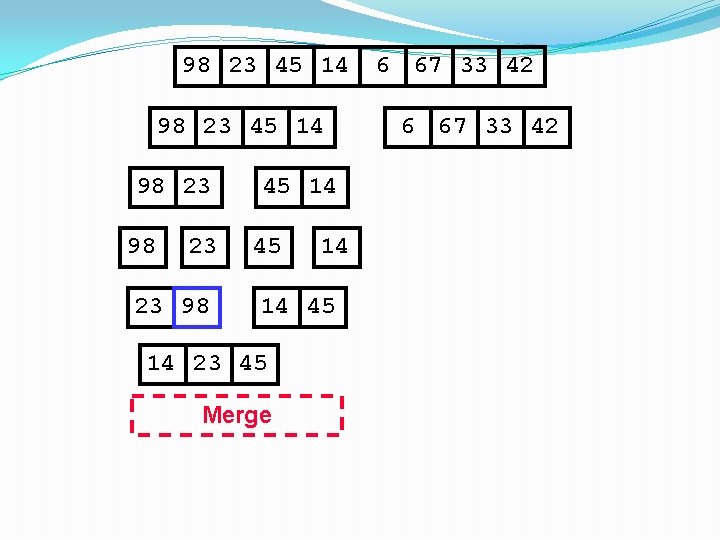
98 23 45 14 98 23 23 98 45 14 14 45 14 Merge 6 67 33 42

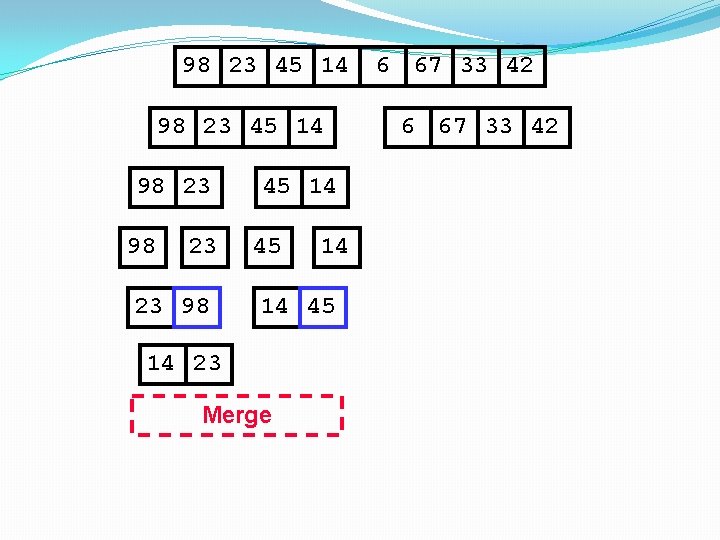
98 23 45 14 98 23 23 98 45 14 14 45 14 23 Merge 6 67 33 42

98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 Merge 6 67 33 42

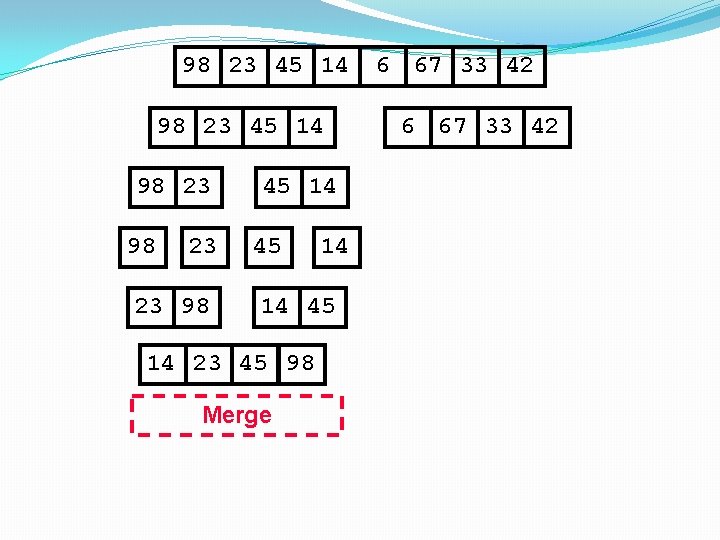
98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 Merge 6 67 33 42

98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 6 67 33 42

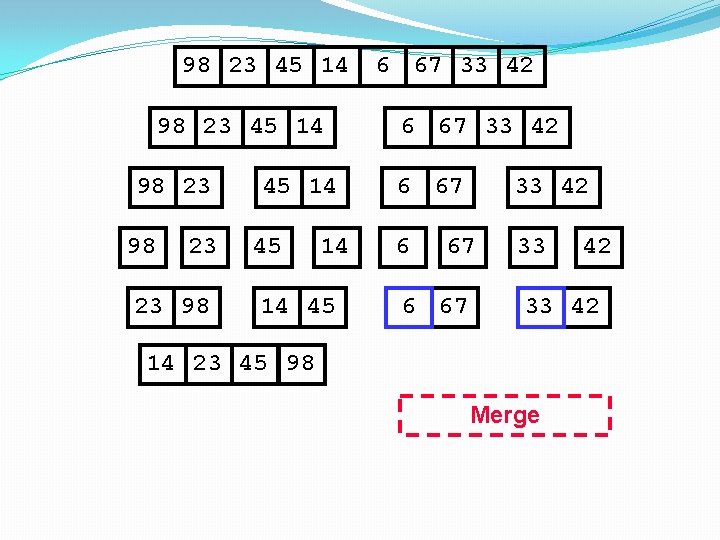
98 23 45 14 98 23 23 98 45 14 6 67 33 42 6 67 14 45 14 23 45 98 Merge 33 42

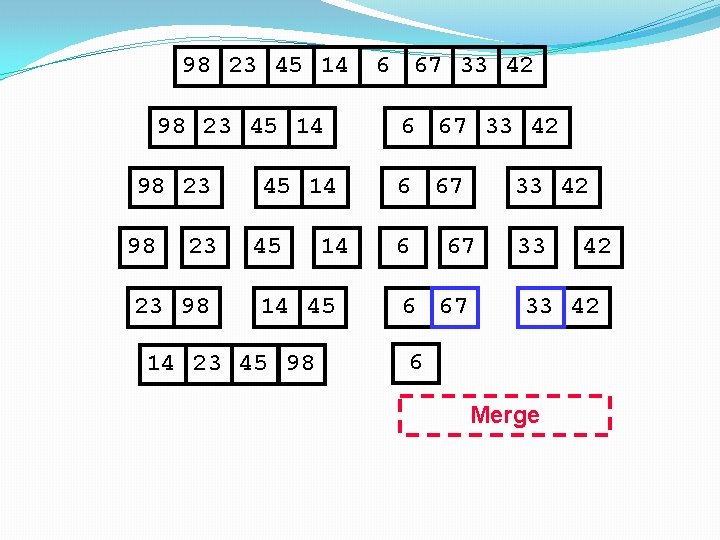
98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 6 67 33 42 6 67 6 Merge 33 42

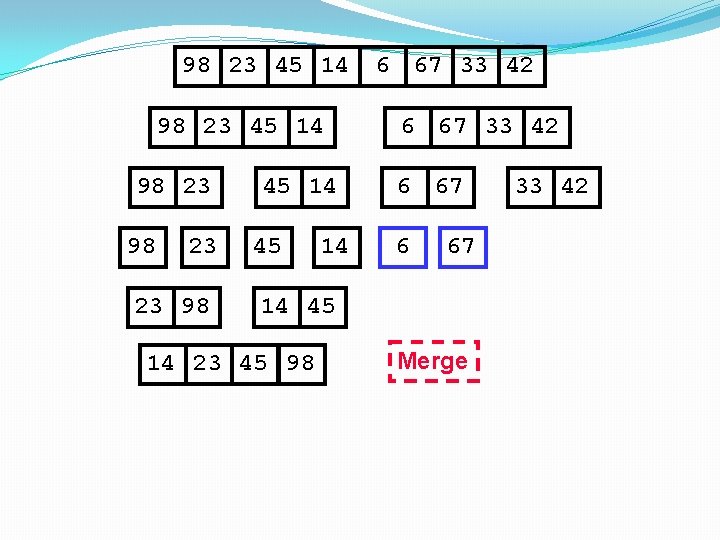
98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 6 67 33 42 6 67 Merge 33 42

98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 6 67 33 42 6 33 67 6 67 42

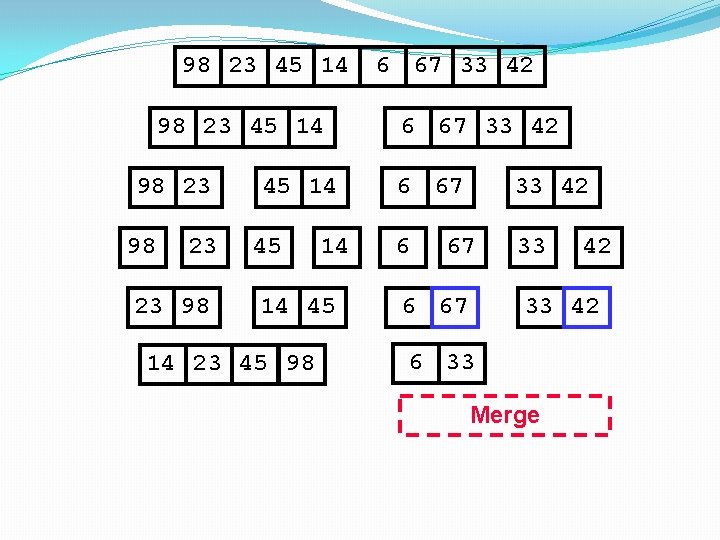
98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 6 67 33 42 6 33 67 42 6 67 Merge

98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 6 67 33 42 6 33 67 6 67 42 33 Merge

98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 6 67 33 42 6 33 67 6 67 42 33 42 Merge

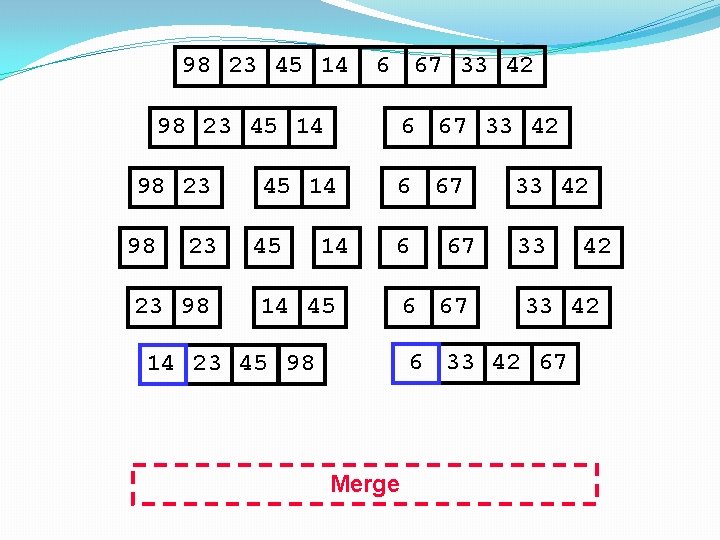
98 23 45 14 98 23 23 98 45 14 14 45 6 67 33 42 6 33 67 6 67 42 33 42 14 23 45 98 Merge

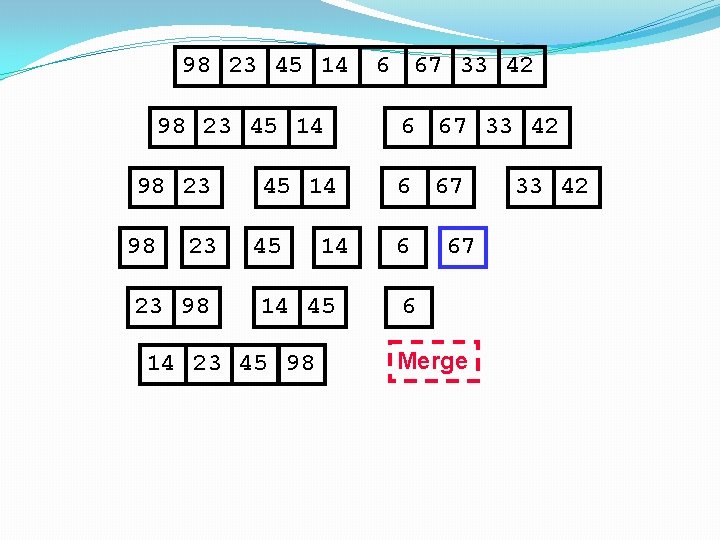
98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 6 67 33 42 6 33 67 6 67 42 33 42 6 Merge

98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 6 67 33 42 6 33 67 6 67 42 33 42 6 33 Merge

98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 6 67 33 42 6 33 67 6 67 42 33 42 6 33 42 Merge

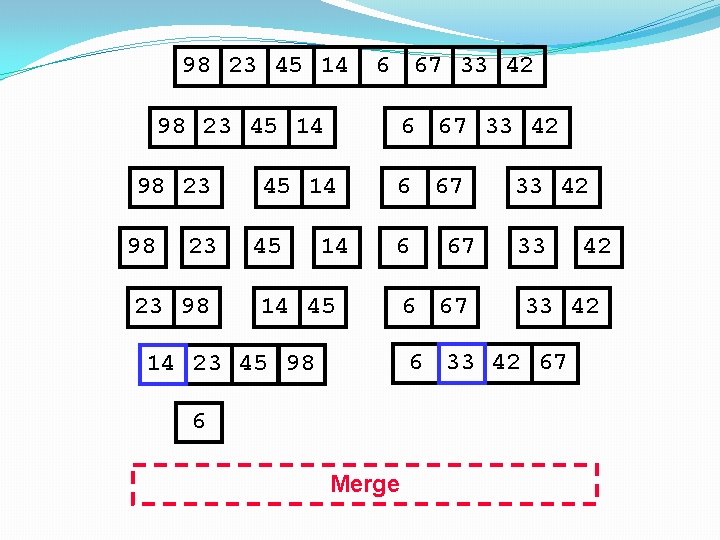
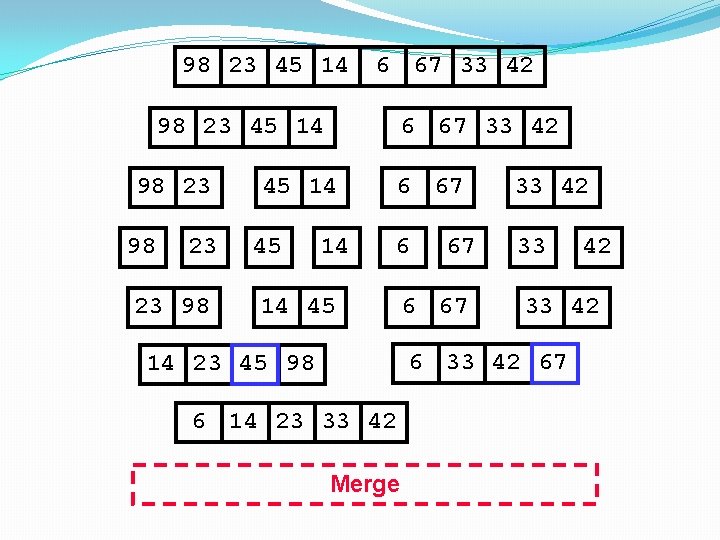
98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 6 67 33 42 6 33 67 6 67 42 33 42 67 Merge

98 23 45 14 6 67 33 42 98 23 45 14 98 23 23 98 6 67 33 42 45 14 6 67 33 42 6 33 14 45 67 6 67 33 42 67 14 23 45 98 Merge 42

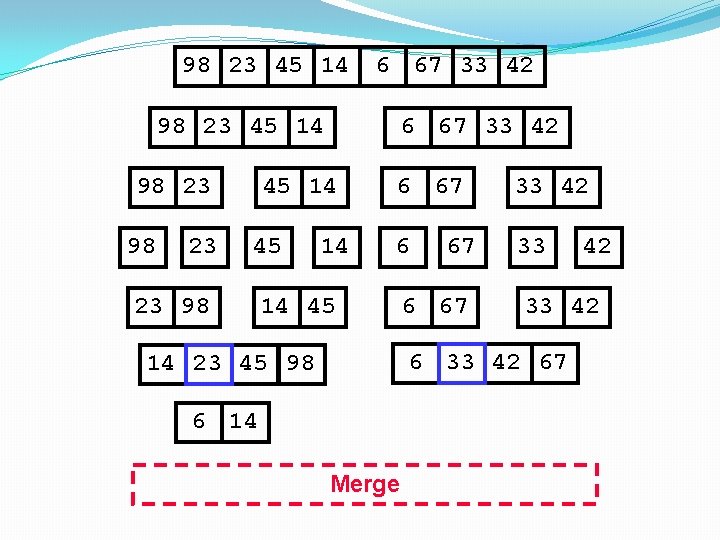
98 23 45 14 6 67 33 42 98 23 45 14 98 23 23 98 6 67 33 42 45 14 6 67 33 42 6 33 14 45 67 6 67 33 42 67 14 23 45 98 6 Merge 42

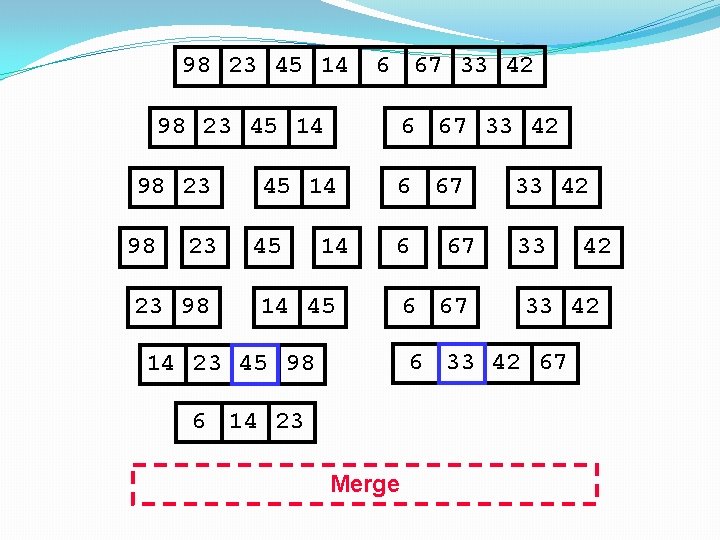
98 23 45 14 6 67 33 42 98 23 45 14 98 23 6 67 33 42 45 14 45 23 98 14 6 67 33 42 6 33 14 45 67 6 67 33 42 67 14 23 45 98 6 14 Merge 42

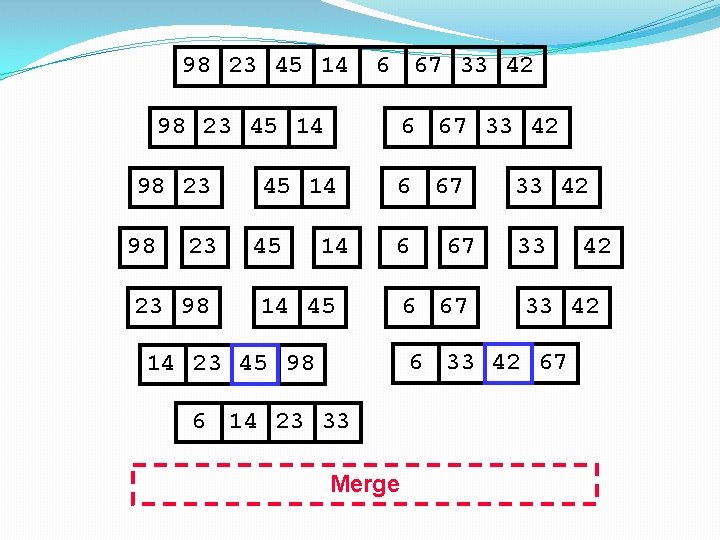
98 23 45 14 6 67 33 42 98 23 45 14 98 23 23 98 6 67 33 42 45 14 6 67 33 42 6 33 14 45 67 6 67 33 42 67 14 23 45 98 6 14 23 Merge 42

98 23 45 14 6 67 33 42 98 23 45 14 98 23 23 98 6 67 33 42 45 14 6 67 33 42 6 33 14 45 67 6 67 33 42 67 14 23 45 98 6 14 23 33 Merge 42

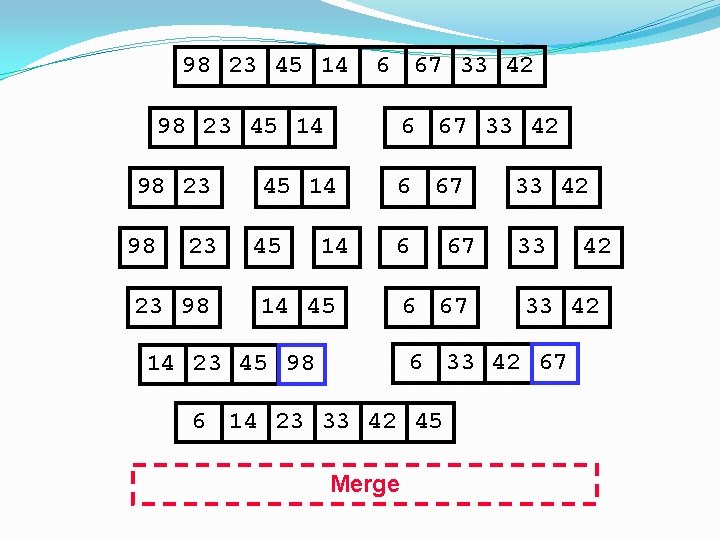
98 23 45 14 6 67 33 42 98 23 45 14 98 23 23 98 6 67 33 42 45 14 6 67 33 42 6 33 14 45 67 6 67 33 42 67 14 23 45 98 6 14 23 33 42 Merge 42

98 23 45 14 6 67 33 42 98 23 45 14 98 23 23 98 6 67 33 42 45 14 6 67 33 42 6 33 14 45 67 6 67 33 42 67 14 23 45 98 6 14 23 33 42 45 Merge 42

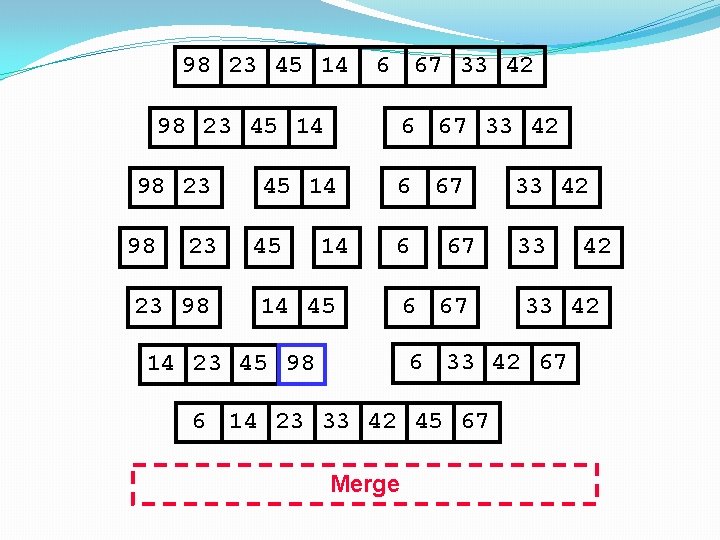
98 23 45 14 6 67 33 42 98 23 45 14 98 23 23 98 6 67 33 42 45 14 6 67 33 42 6 33 14 45 67 6 67 33 42 67 14 23 45 98 6 14 23 33 42 45 67 Merge 42

98 23 45 14 6 67 33 42 98 23 45 14 98 23 23 98 6 67 33 42 45 14 6 67 33 42 6 33 14 45 67 6 67 33 42 67 14 23 45 98 6 14 23 33 42 45 67 98 Merge 42

98 23 45 14 98 23 23 98 45 14 14 45 14 23 45 98 6 67 33 42 6 33 67 6 67 42 33 42 67 6 14 23 33 42 45 67 98

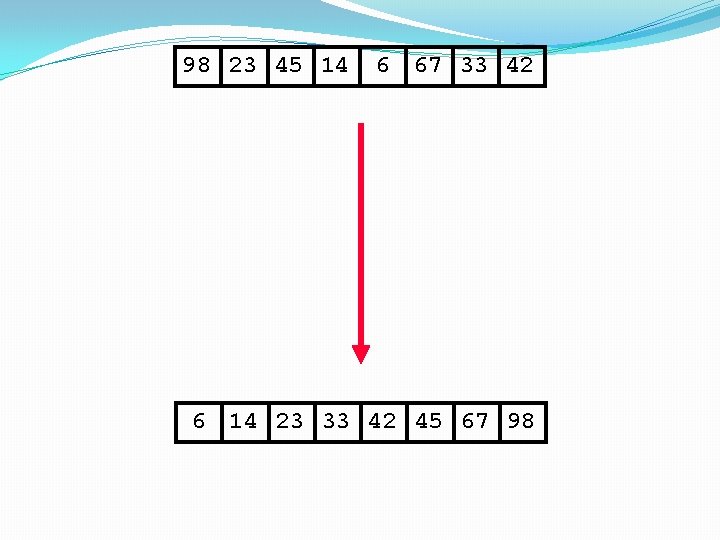
98 23 45 14 6 67 33 42 6 14 23 33 42 45 67 98

Algorithm Mergesort(Passed an array) if array size > 1 Divide array in half Call Mergesort on first half. Call Mergesort on second half. Merge two halves. Merge(Passed two arrays) Compare leading element in each array Select lower and place in new array. (If one input array is empty then place remainder of other array in output array)

Pseudo code Mergesort(A, low, high) If (low<high)then { Mid: = (low+high)/2 //split list in 2 Mergesort(A, low, mid) //1 st sublist Mergesort(A, mid+1, high) //2 nd sublist Merge(A, low, mid, high) } // merging of 2 list

Merge(A[0…n-1], low, mid, high) k=low i=low j= mid+1 Loop: while(i<=mid &&j<=high) do if(A[i]<=A[j]) then temp[k]=A[i] increment i increment k else temp[k]=A[j] increment j increment k while loop ends

//copy remaining elements of left part(sublist 1) while(i<=mid)d 0 temp[k]=A[i] increment i Increment k Loop ends //copy remaining elements of right part(sublist 2) while(j<=high)do temp[k]=A[j] increment j increment k Loop ends

Summary �Divide the unsorted collection into two �Until the sub-arrays only contain one element �Then merge the sub-problem solutions together �Best Case, Average Case, and Worst Case = O(N log. N)