Sorting Sorting Sorting is important Things that would

Sorting

Sorting • Sorting is important! • Things that would be much more difficult without sorting: – finding a telephone number – looking up a word in the dictionary – finding a book in the library – buying a cd – renting a movie – reading a book – reading new email

How to sort? • Think about sorting a hand of cards

Comparison-based sorting • Sort by making comparisons • Ordering decision based on comparison of elements • Requires that elements are comparable – have a natural order • numerical – numbers • lexicographic (alphabetical) – characters • chronological – dates

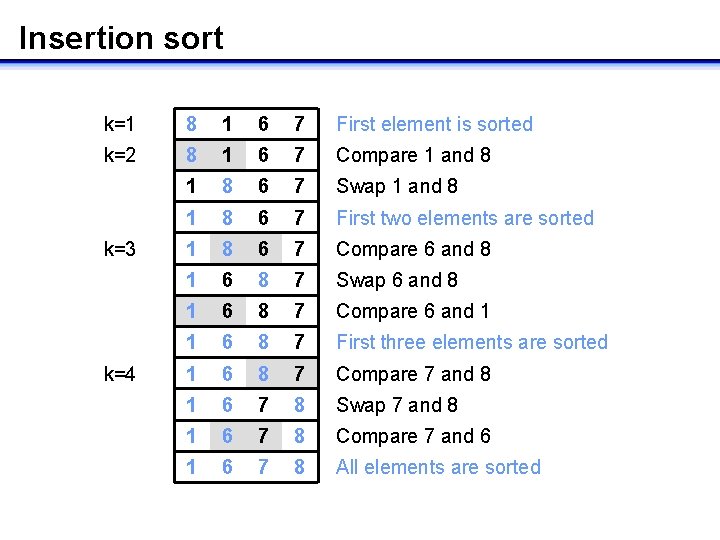
Insertion sort • Input: n elements in arbitrary order • For k = 2, …, n – compare elements in position k and position k-1 • if elements are unordered, swap them – compare elements in position k-1 and position k-2 • if elements are unordered, swap them – continue until you compare ordered elements or all elements have been swapped • once elements are sorted, they remain sorted relative to each other • Output: n elements in sorted order

Insertion sort k=1 8 1 6 7 First element is sorted k=2 8 1 6 7 Compare 1 and 8 1 8 6 7 Swap 1 and 8 1 8 6 7 First two elements are sorted 1 8 6 7 Compare 6 and 8 1 6 8 7 Swap 6 and 8 1 6 8 7 Compare 6 and 1 1 6 8 7 First three elements are sorted 1 6 8 7 Compare 7 and 8 1 6 7 8 Swap 7 and 8 1 6 7 8 Compare 7 and 6 1 6 7 8 All elements are sorted k=3 k=4

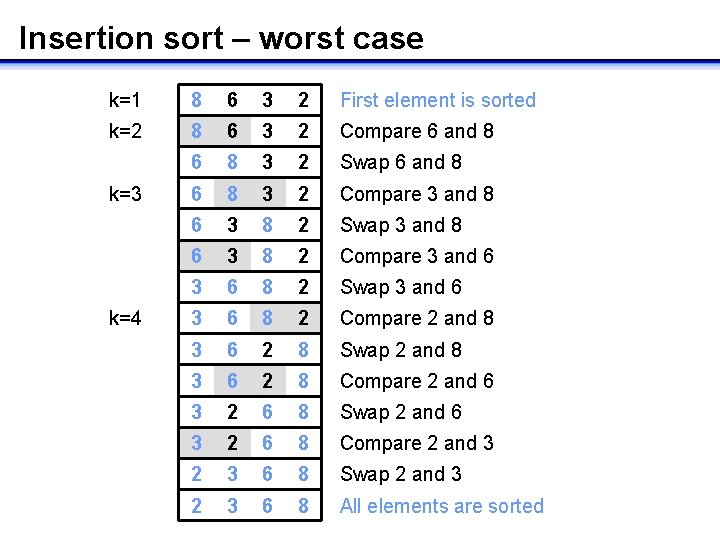
Worst case behavior … • At each step k – compare element in position k with previous elements until first k elements are in sorted order • In the worst case, we compare each element with all of the previous elements – at step 2 we make 1 comparison – at step 3 we make 2 comparisons – at step n we make n-1 comparisons • Worst case behavior occurs when the array is in reverse sorted order

Insertion sort – worst case k=1 8 6 3 2 First element is sorted k=2 8 6 3 2 Compare 6 and 8 6 8 3 2 Swap 6 and 8 6 8 3 2 Compare 3 and 8 6 3 8 2 Swap 3 and 8 6 3 8 2 Compare 3 and 6 3 6 8 2 Swap 3 and 6 3 6 8 2 Compare 2 and 8 3 6 2 8 Swap 2 and 8 3 6 2 8 Compare 2 and 6 3 2 6 8 Swap 2 and 6 3 2 6 8 Compare 2 and 3 2 3 6 8 Swap 2 and 3 2 3 6 8 All elements are sorted k=3 k=4

Best case behavior • What if the elements are already sorted? 1 3 5 6 7 9 • How many comparisons per element will be made by insertion sort?

Insertion sort – best case k=1 1 3 5 6 7 9 First element is sorted k=2 1 3 5 6 7 9 Compare 3 and 1 1 3 5 6 7 9 First two elements are sorted 1 3 5 6 7 9 Compare 5 and 3 1 3 5 6 7 9 First three elements are sorted 1 3 5 6 7 9 Compare 6 and 5 1 3 5 6 7 9 First four elements are sorted 1 3 5 6 7 9 Compare 7 and 6 1 3 5 6 7 9 First five elements are sorted 1 3 5 6 7 9 Compare 9 and 7 1 3 5 6 7 9 All elements are sorted k=3 k=4 k=5 k=6

Comparisons in insertion sort • Worst case – element k requires (k-1) comparisons – total number of comparisons: 0+1+2+ … + (n-1) = ½ (n)(n-1) = ½ (n 2 -n) • Best case – elements 2 through n each require one comparison – total number of comparisons: 1+1+1+ … + 1 = n-1 (n-1) times

The divide-and-conquer approach • Insertion sort uses an incremental approach – puts elements in correct place one at a time • We can design more efficient sorting algorithms using the divide-and-conquer approach: – Divide the problem into a number of subproblems – Conquer the subproblems by solving them recursively until the subproblems are small enough to solve directly – Merge the solutions for the subproblems into the solution for the original problem

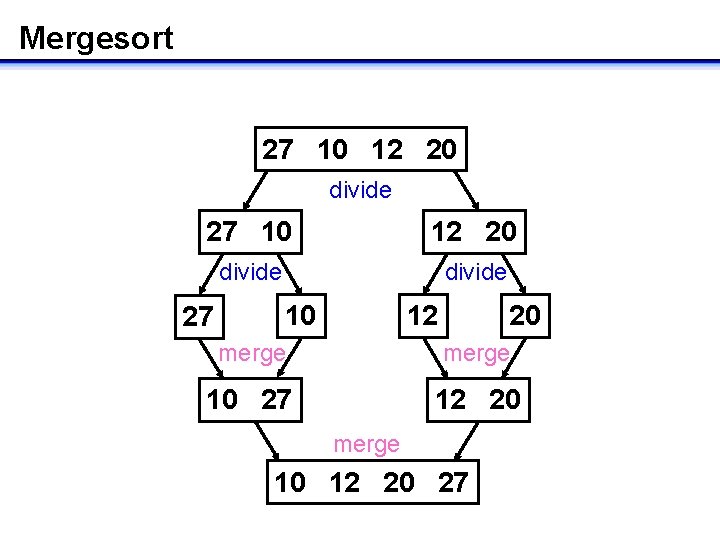
Mergesort • Divide-and-conquer sorting algorithm • Given a list of n elements in arbitrary order – Divide – Conquer – Merge the list of n elements into two sub-lists of n/2 elements each sub-list by sorting it recursively the solutions to all sub-lists into a single sorted list of n elements

Mergesort 27 10 12 20 divide 27 10 12 20 merge 10 27 12 20 merge 10 12 20 27

Merging • Idea: – suppose you have an unsorted deck of cards – you split the deck in half, give half to your friend to sort and sort the other half yourself – now you have two half-decks, each sorted – how do you combine them into a single sorted deck?

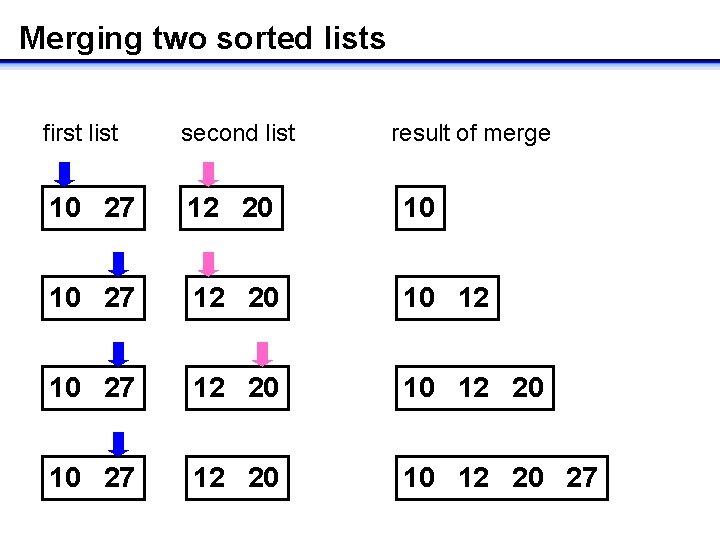
Merging two sorted lists first list second list result of merge 10 27 12 20 10 12 20 27

Comparisons in mergesort • Dividing a list of elements requires no comparisons – just compute midpoint • Merging two lists of size m requires at least m and at most 2 m - 1 comparisons – one comparison at each step of the merge – elements in result list are not compared again – add at least one element to result at each step • Total number of comparisons is the sum of the number of comparisons made at each merge