Sorting Networks Characteristics Implemented in hardware Parallel operations

Sorting Networks • Characteristics – Implemented in hardware – Parallel operations are possible • The basic unit: a comparator – Comparison occurs when both inputs are available – Comparison time is O(1) – A comparator sorts two inputs

A Comparison Network • Characteristics: four inputs, four outputs, five comparators, depth of three • This comparison network is a sorter; how can this be explained in common sense terms?

Some Thought Problems • Why must any sorting network with n inputs have at least a depth of lg n ? • Why must a sorting network with n inputs perform at least n lg n comparisons ?

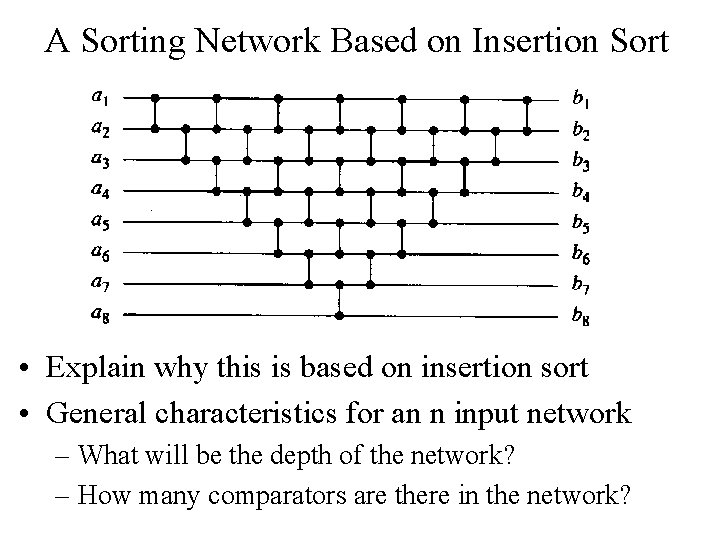
A Sorting Network Based on Insertion Sort • Explain why this is based on insertion sort • General characteristics for an n input network – What will be the depth of the network? – How many comparators are there in the network?

The Zero-One Principle - 1 • The basic idea is that is you can prove an n input comparison network sorts the 2 n inputs with 0 or 1 correctly then it will sort any data correctly • The proof of the lemma has two basic steps • Induction is then used to prove the lemma

The Zero-One Principle - 2 • Induction is based on the depth of the network • The result for depth zero is trivial • For depth d, it is proved for depth d+1 using the result on the previous page • The outputs are at a specific depth, so it is true at the outputs too • An example with f = x/2

The Zero-One Principle - 3

A Bitonic Sorting Network • What is a bitonic sequence? – A sequence that increases then decreases, such as { 3, 5, 7, 9, 12, 14, 11, 8, 7, 4, 2 } or such a sequence that has been circularly shifted – For inputs of 0 and 1, a bitonic sequence has one of two forms: 0 i 1 j 0 k or 1 i 0 j 1 k • Steps in the process – Build a “half-cleanser” network – Build a bitonic sorter recursively by halving the size from n to n/2 to n/4 until a base case of 2 is reached – Show the computation time is lg n

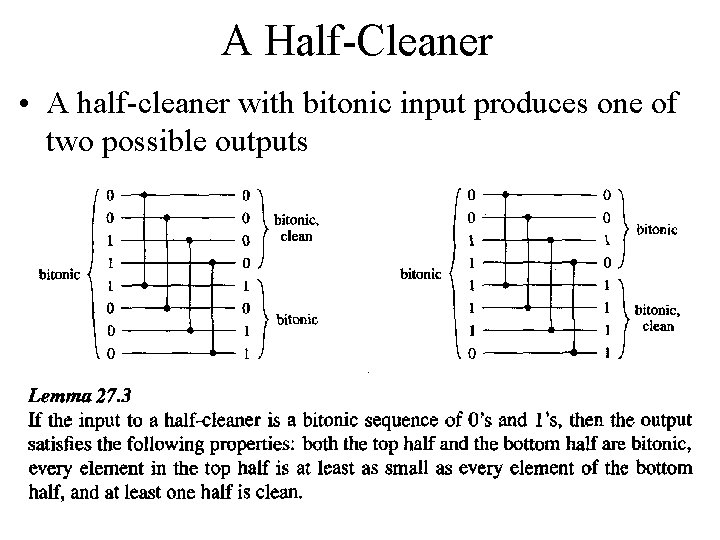
A Half-Cleaner • A half-cleaner with bitonic input produces one of two possible outputs

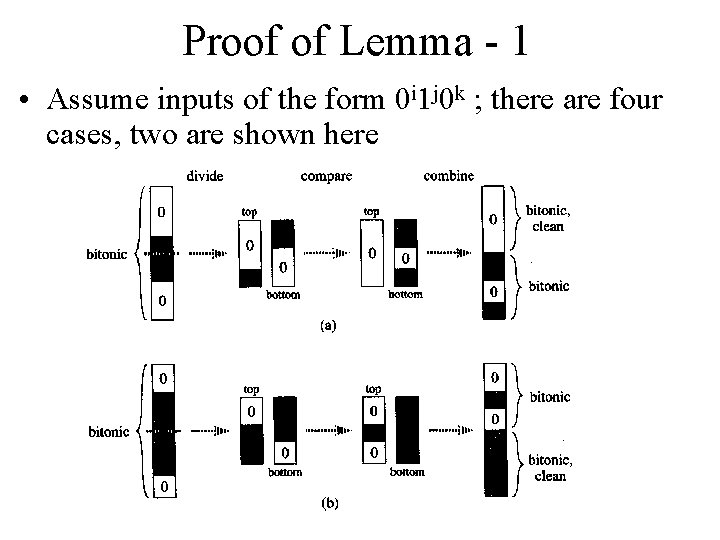
Proof of Lemma - 1 • Assume inputs of the form 0 i 1 j 0 k ; there are four cases, two are shown here

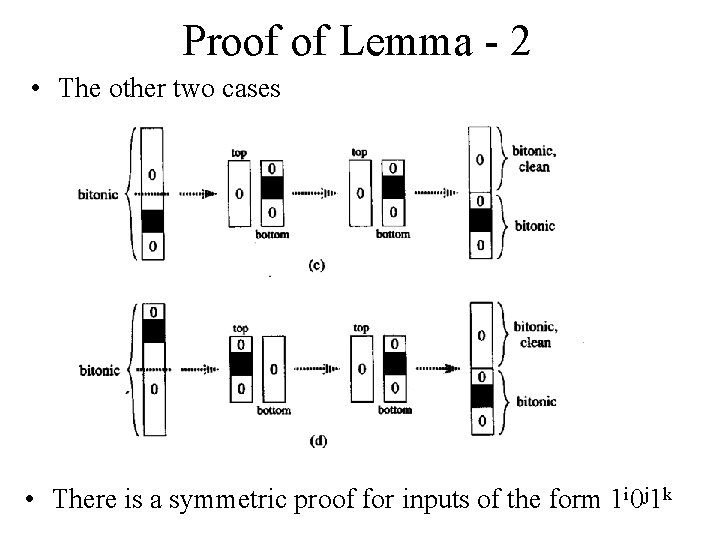
Proof of Lemma - 2 • The other two cases • There is a symmetric proof for inputs of the form 1 i 0 j 1 k

Building the Bitonic Sorter • Steps – A half-cleanser of size n is introduced – Two parallel bitonic sorters of size n/2 are attached – A recursive unraveling continues until the base case is reached – The final circuit is a bitonic sorter of size n

Depth of the Sorter • This result has been shown for a zero-one bitonic sorter • In a manner analogous to the zero-one theorem, it can be shown this same network can sort bitonic sequences of any arbitrary numbers

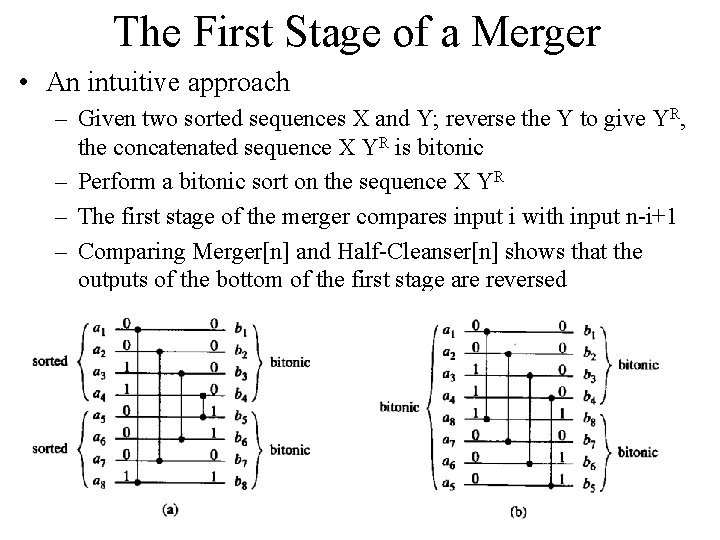
The First Stage of a Merger • An intuitive approach – Given two sorted sequences X and Y; reverse the Y to give YR, the concatenated sequence X YR is bitonic – Perform a bitonic sort on the sequence X YR – The first stage of the merger compares input i with input n-i+1 – Comparing Merger[n] and Half-Cleanser[n] shows that the outputs of the bottom of the first stage are reversed

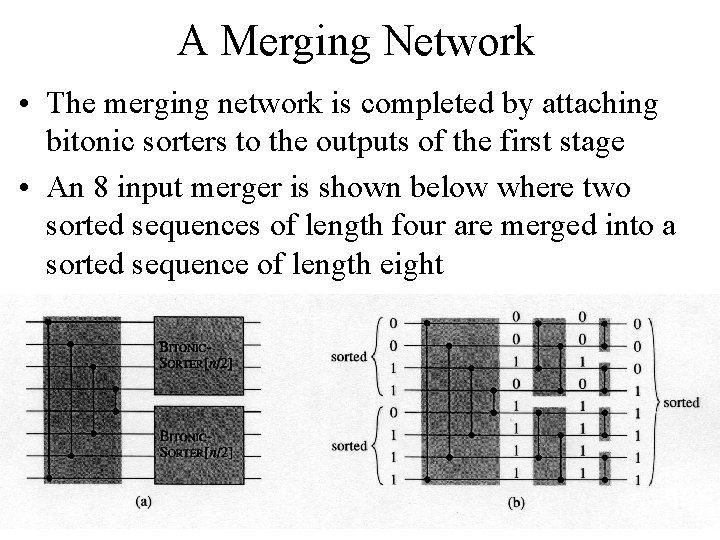
A Merging Network • The merging network is completed by attaching bitonic sorters to the outputs of the first stage • An 8 input merger is shown below where two sorted sequences of length four are merged into a sorted sequence of length eight

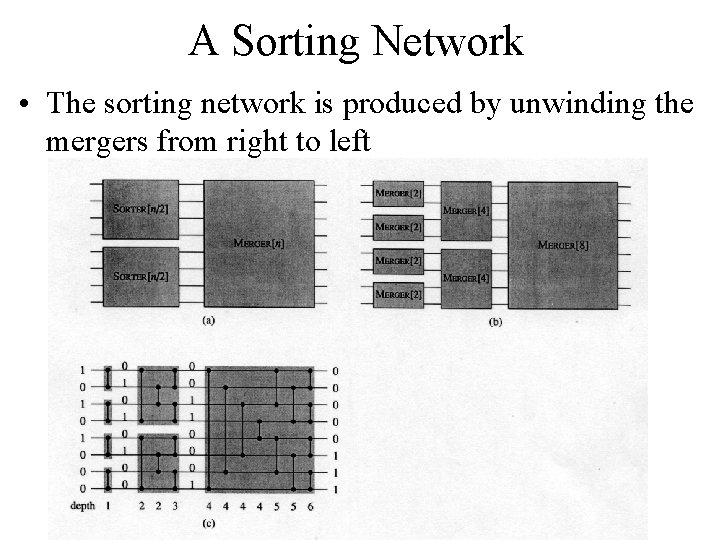
A Sorting Network • The sorting network is produced by unwinding the mergers from right to left

The Depth of Sorter[n] • Calculating the depth recursively – The depth of sorter[n] is the depth of sorter[n/2] plus the depth of the merger[n], which is lg n – Note the two sorter[n/2] run in parallel so it only appears once in the recurrence relation

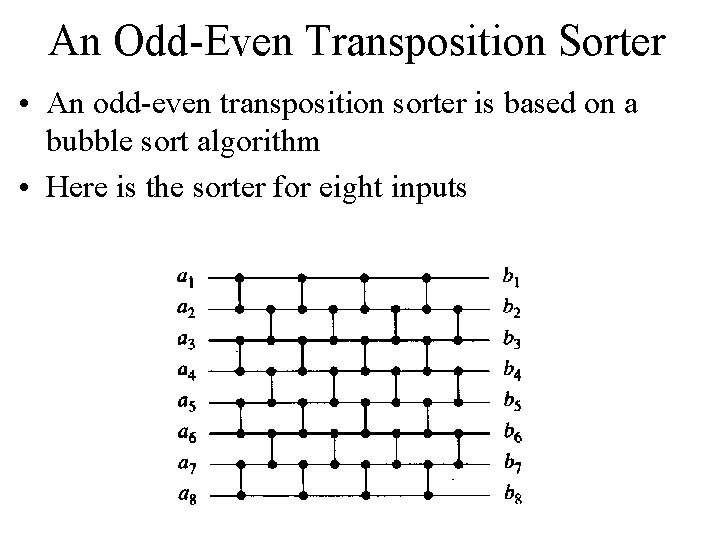
An Odd-Even Transposition Sorter • An odd-even transposition sorter is based on a bubble sort algorithm • Here is the sorter for eight inputs

Name(s)_______________ • Use the zero-one principle to prove this comparison network is a sorting network

Name(s)_______________ • How many bitonic sequences containing 0 or 1 are there? • Prove a bitonic sorter of size n, a power of 2, contains exactly ( n lg n) comparators

Name(s)_______________ • Design a network that merges 1 item with n-1 sorted items to produce n sorted items • Show that to produce a sequence of length n, the merger must have a depth of at least lg n

Name(s)_______________ • How many comparators are needed to build sorter[n] ? (assume n is a power of 2) • Prove the depth of sorter[n] is exactly (lg n) (lg n + 1)/2

Name(s)_______________ • How many comparators are needed to build odd-even[n] ? (assume n is a power of 2) • What is the depth of odd-even[n] ?

Name(s)_______________ • How many comparators are needed to build insertion_sorter[n] ? (assume n is a power of 2) • What is the depth of insertion_sorter[n] ?