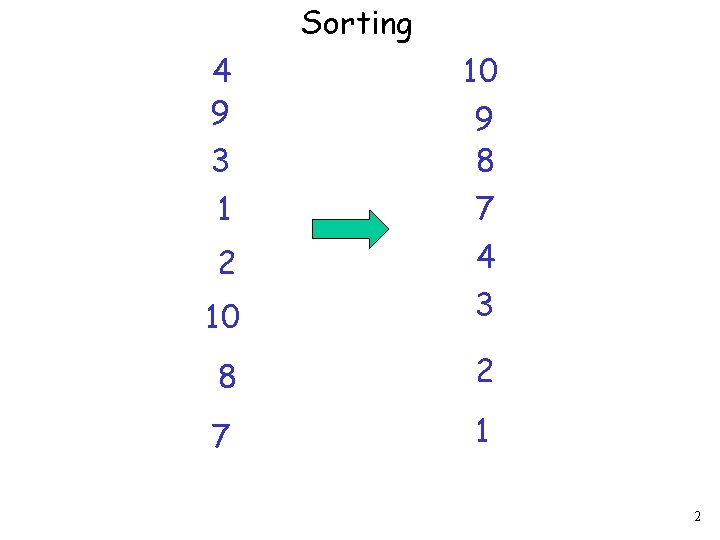
Sorting Networks 1 Sorting 4 9 3 1









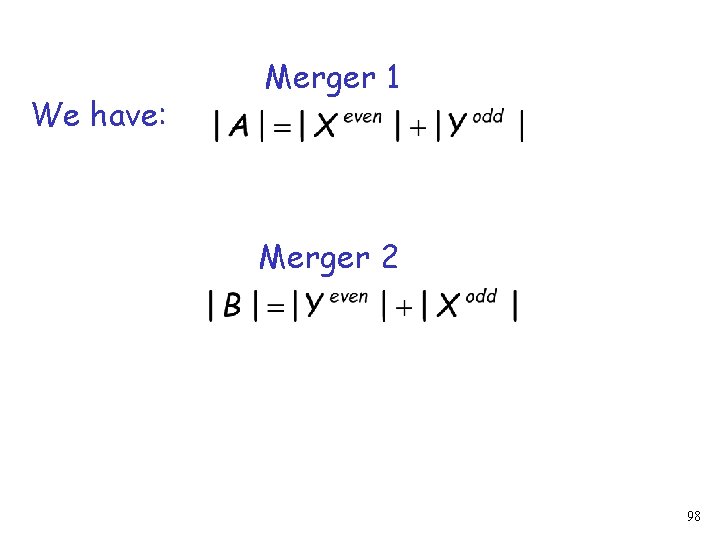
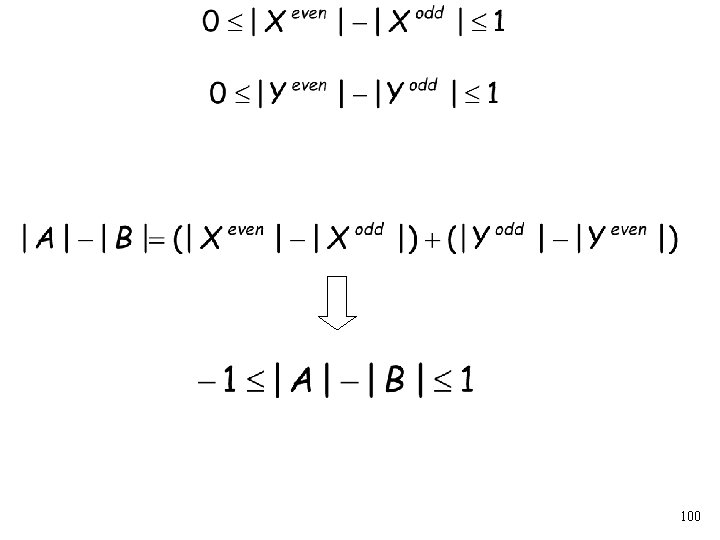
- Slides: 102

Sorting Networks 1

Sorting 4 9 3 1 2 10 9 8 7 4 10 3 8 2 7 1 2

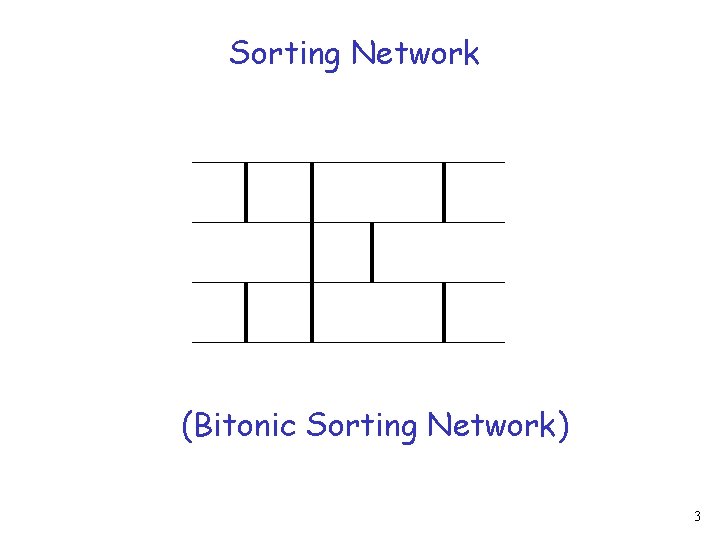
Sorting Network (Bitonic Sorting Network) 3

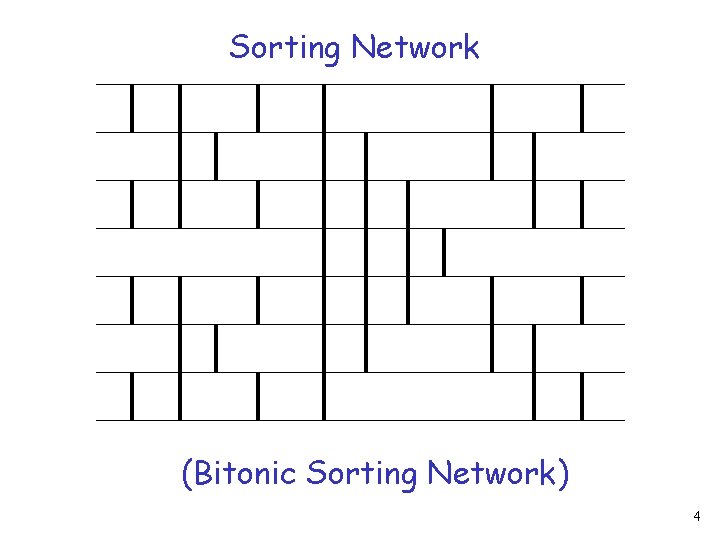
Sorting Network (Bitonic Sorting Network) 4

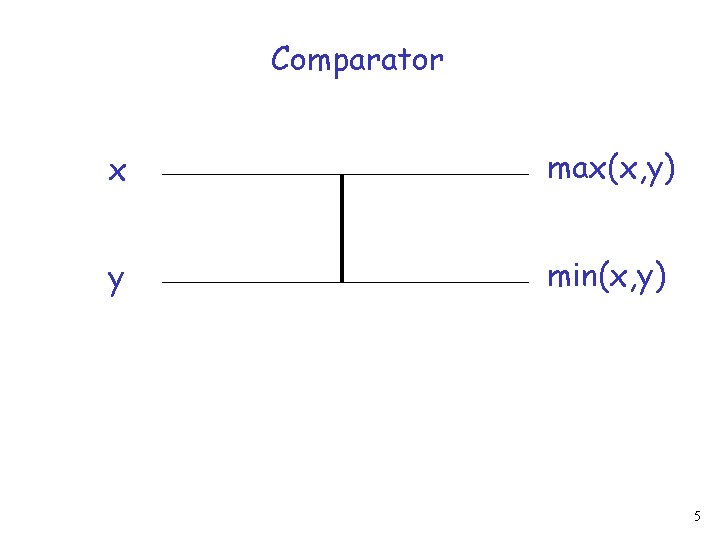
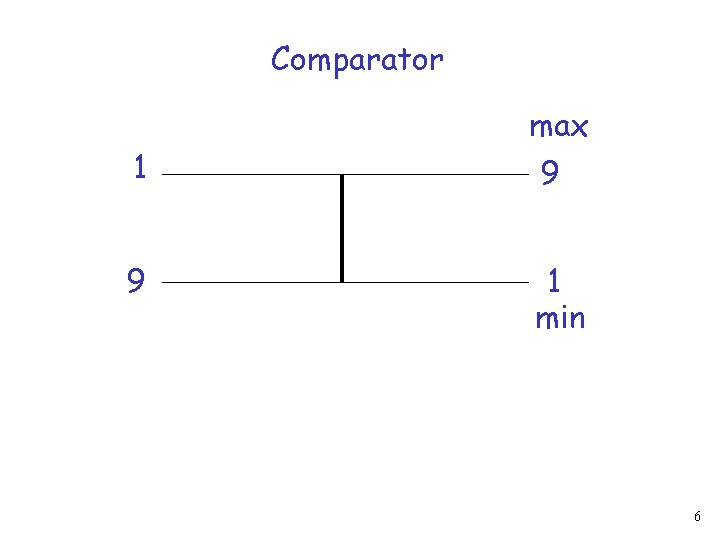
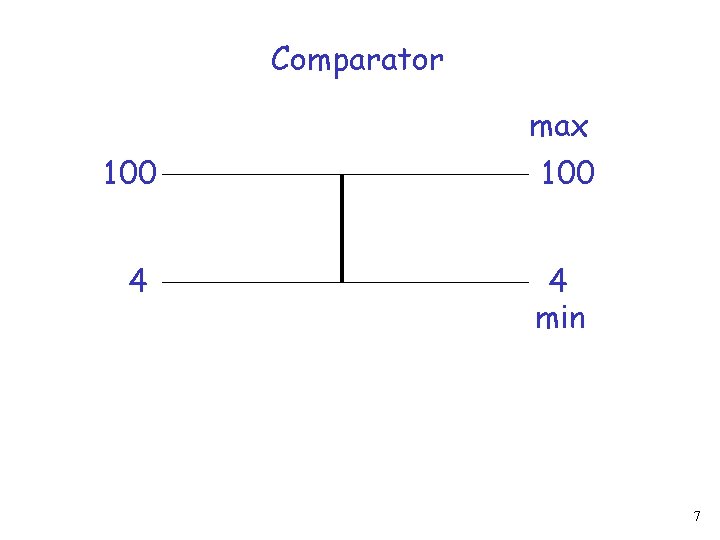
Comparator x max(x, y) y min(x, y) 5

Comparator 1 9 max 9 1 min 6

Comparator max 100 4 4 min 7

8

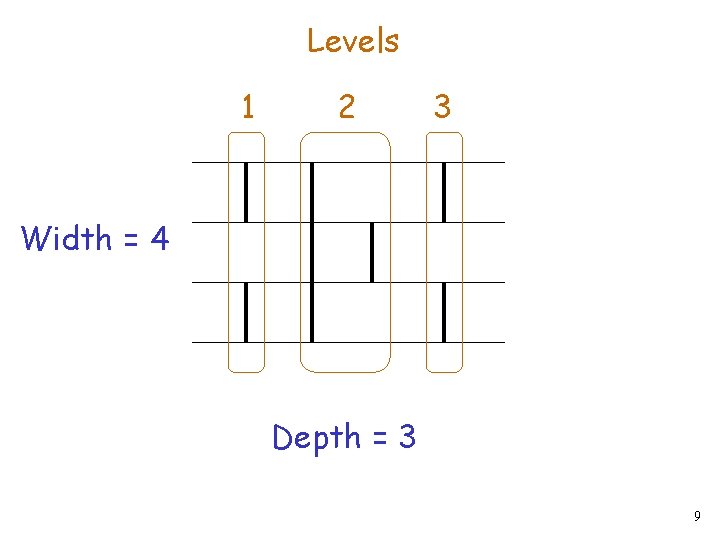
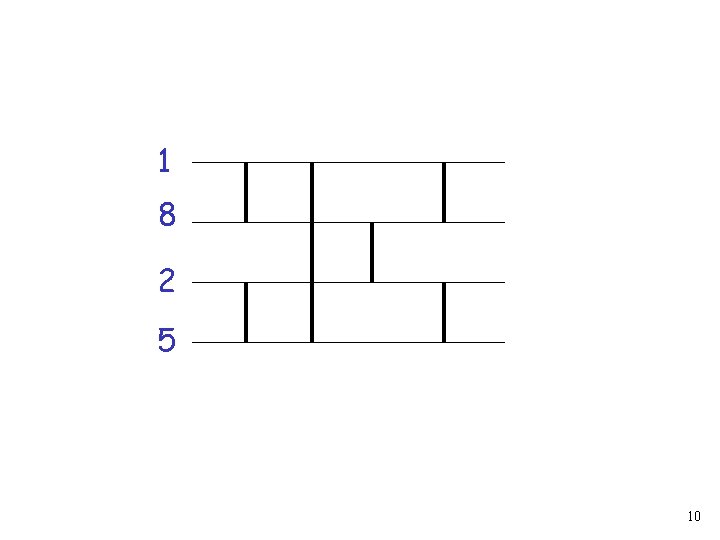
Levels 1 2 3 Width = 4 Depth = 3 9

1 8 2 5 10

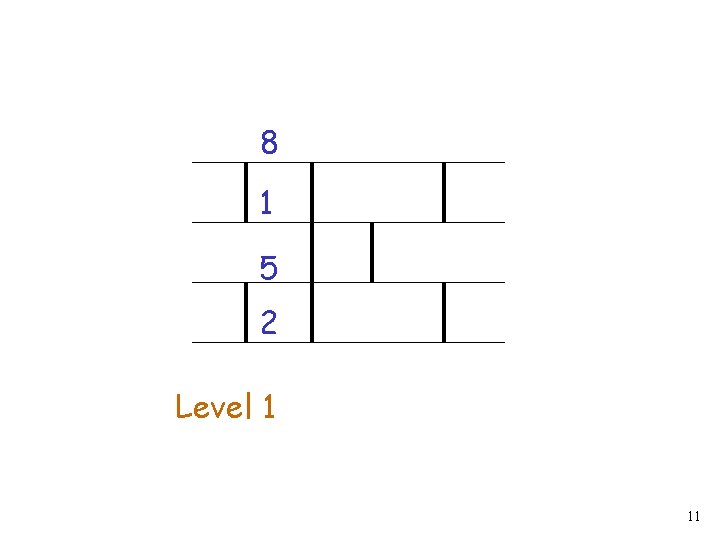
8 1 5 2 Level 1 11

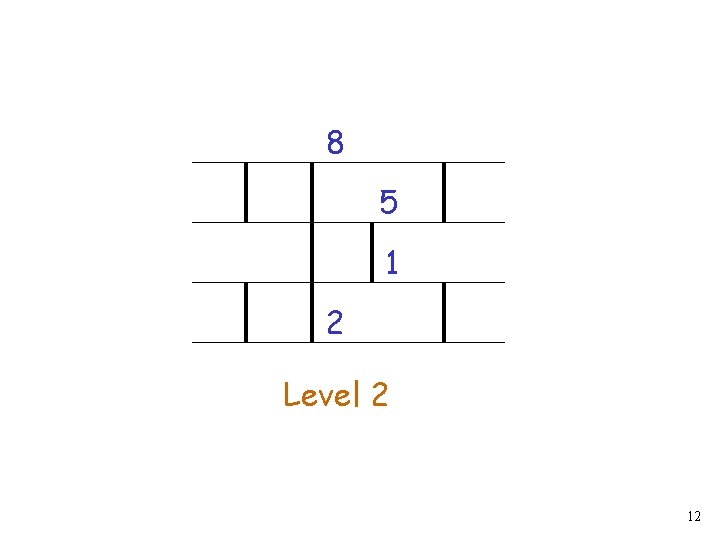
8 5 1 2 Level 2 12

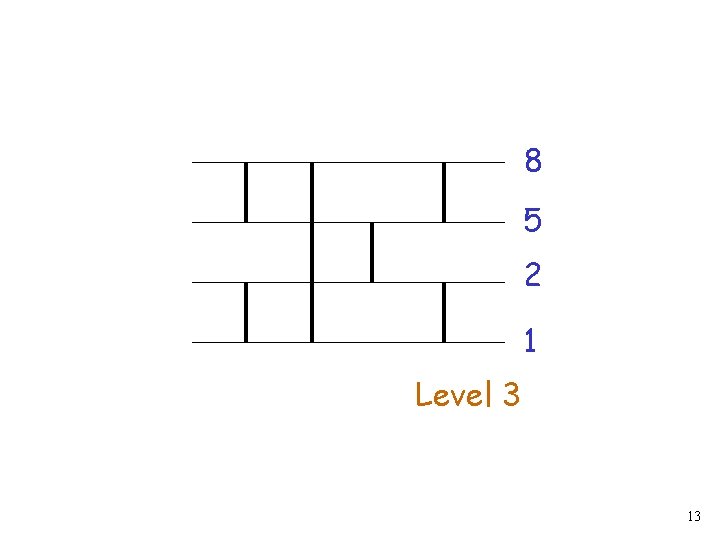
8 5 2 1 Level 3 13

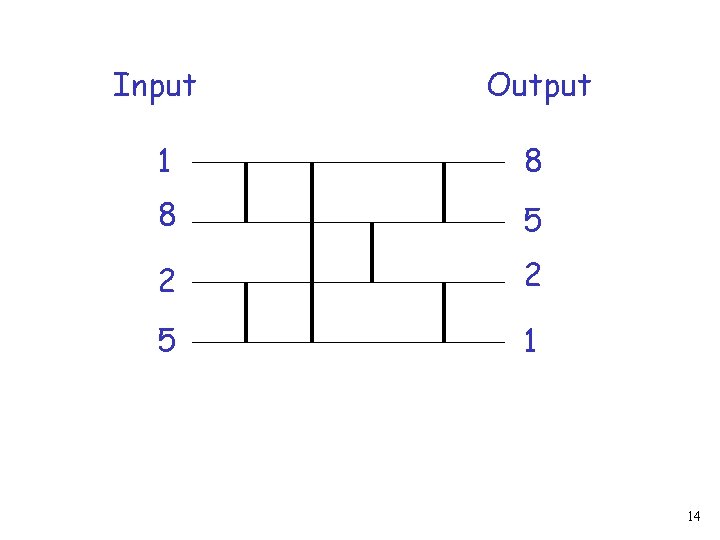
Input Output 1 8 8 5 2 2 5 1 14

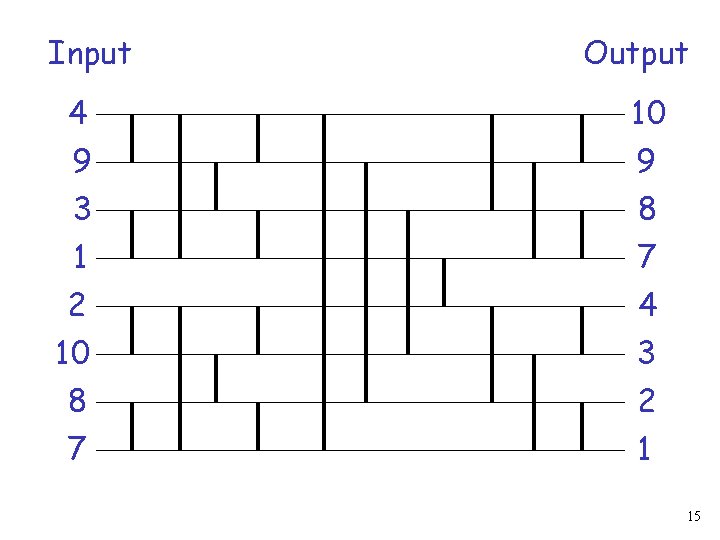
Input Output 4 10 9 3 1 9 8 7 2 10 8 7 4 3 2 1 15

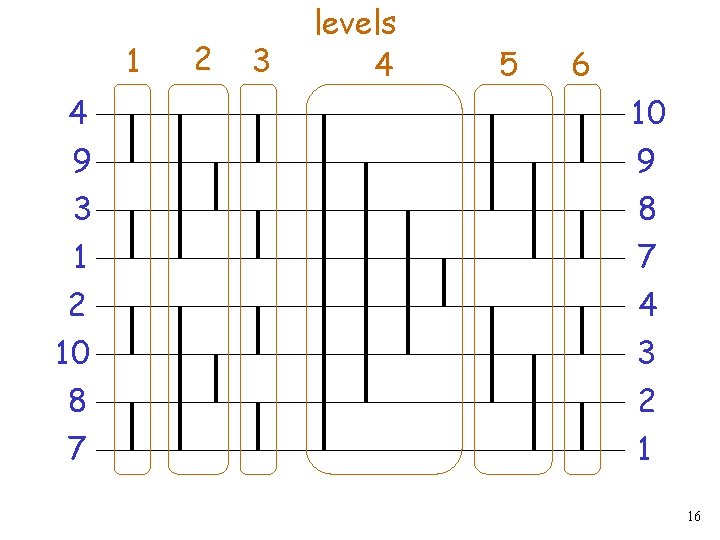
1 2 3 levels 4 5 6 4 10 9 3 1 9 8 7 2 10 8 7 4 3 2 1 16

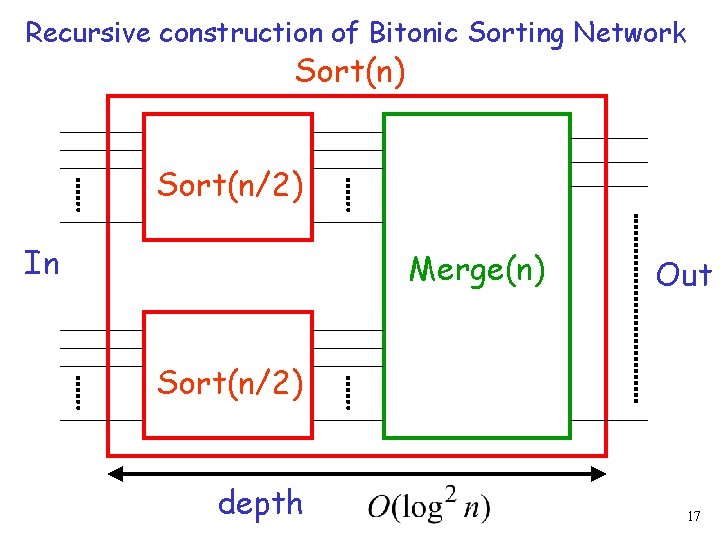
Recursive construction of Bitonic Sorting Network Sort(n) Sort(n/2) In Merge(n) Out Sort(n/2) depth 17

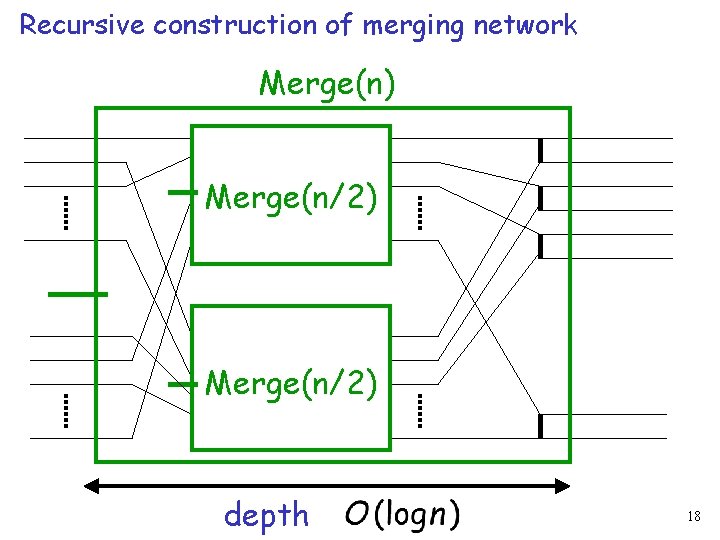
Recursive construction of merging network Merge(n) Merge(n/2) depth 18

Induction Basis Sort(2) Merge(2) 19

Width Sorting network depth: Merger width Total depth 20

Counting Networks 21

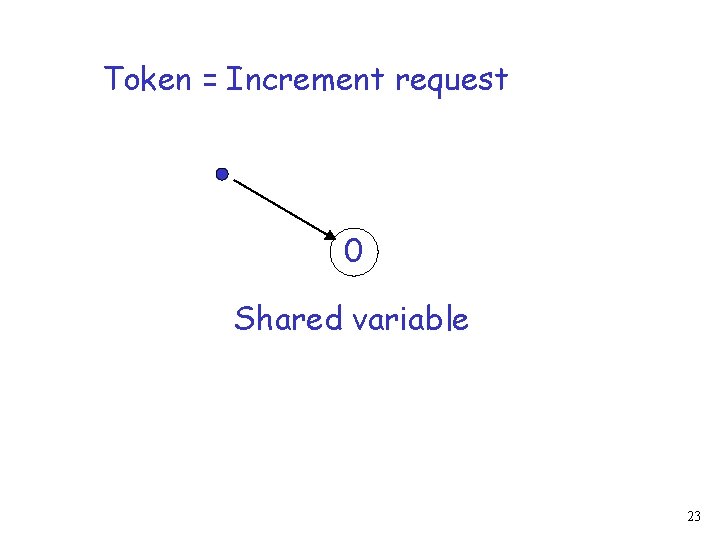
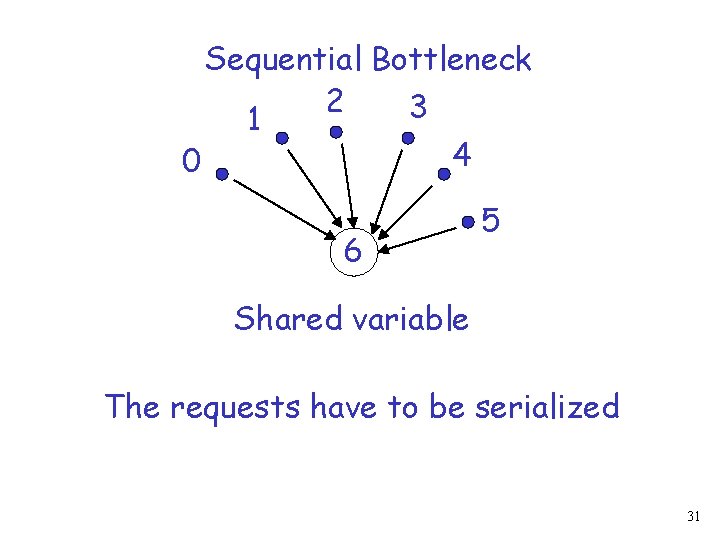
The Counting Problem 0 Shared variable 22

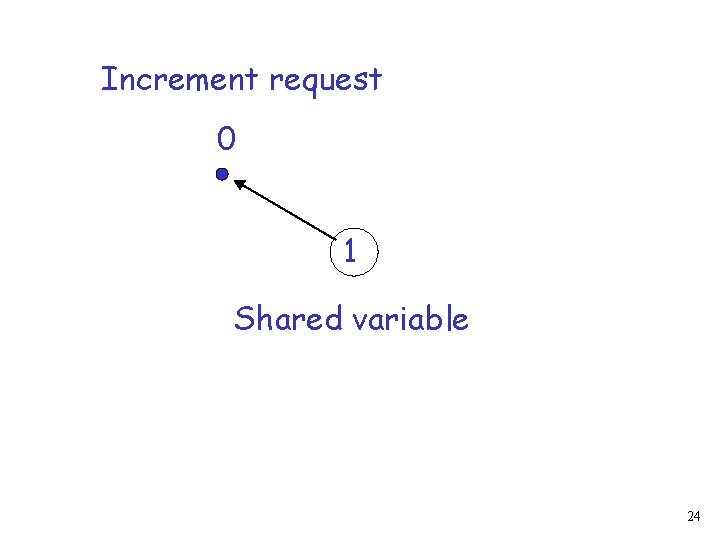
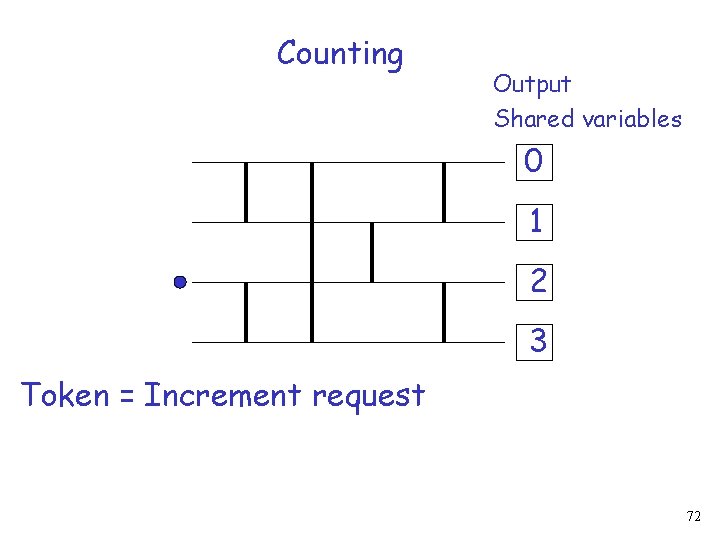
Token = Increment request 0 Shared variable 23

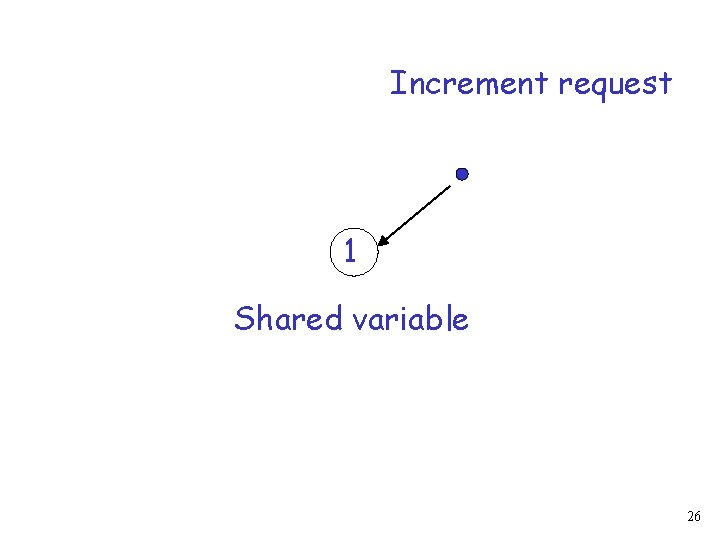
Increment request 0 1 Shared variable 24

1 Shared variable 25

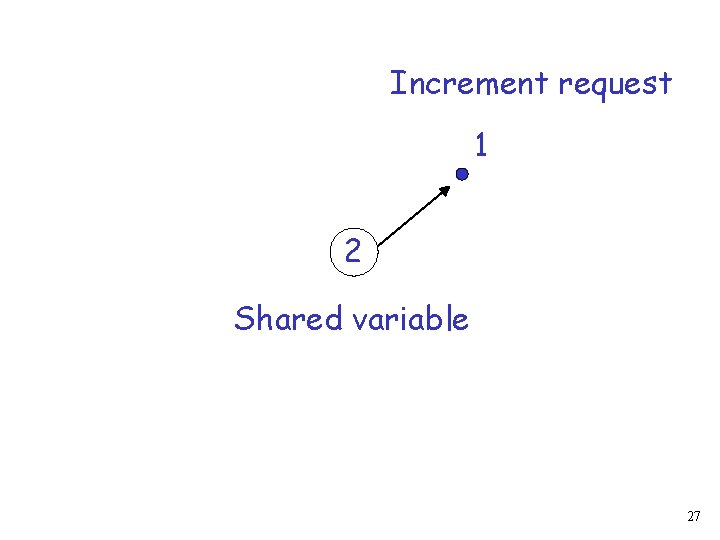
Increment request 1 Shared variable 26

Increment request 1 2 Shared variable 27

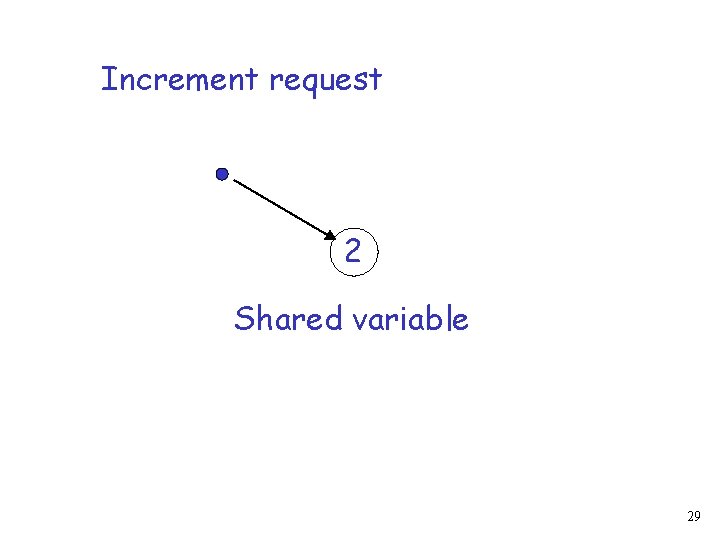
2 Shared variable 28

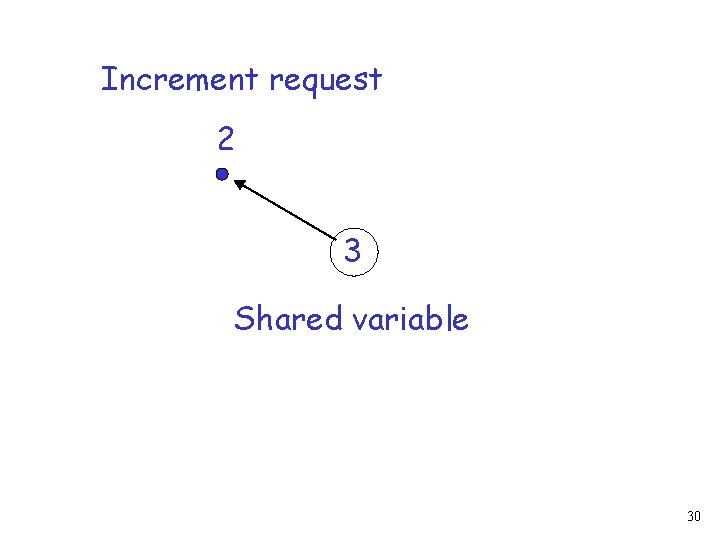
Increment request 2 Shared variable 29

Increment request 2 3 Shared variable 30

Sequential Bottleneck 2 3 1 4 0 6 5 Shared variable The requests have to be serialized 31

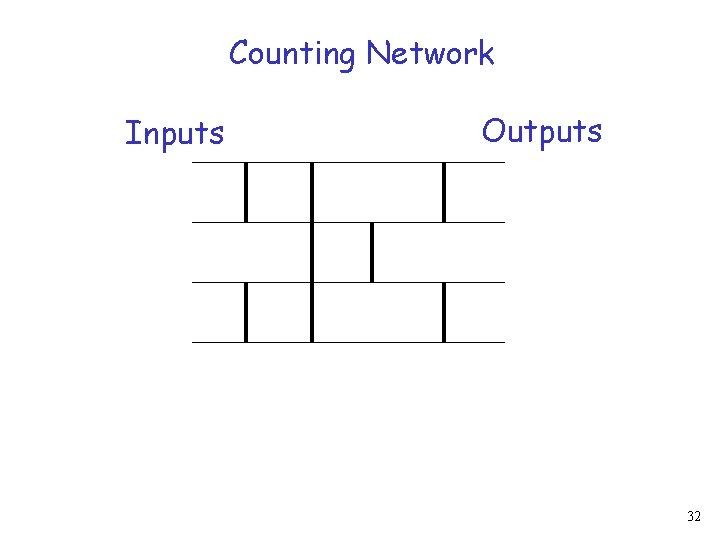
Counting Network Inputs Outputs 32

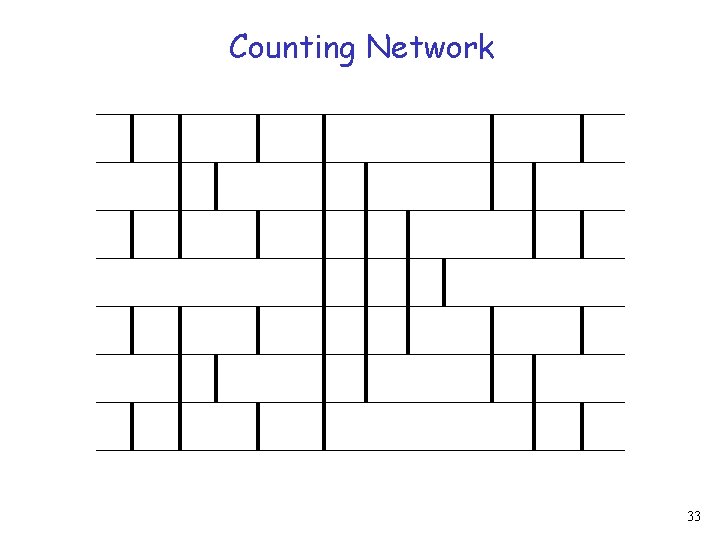
Counting Network 33

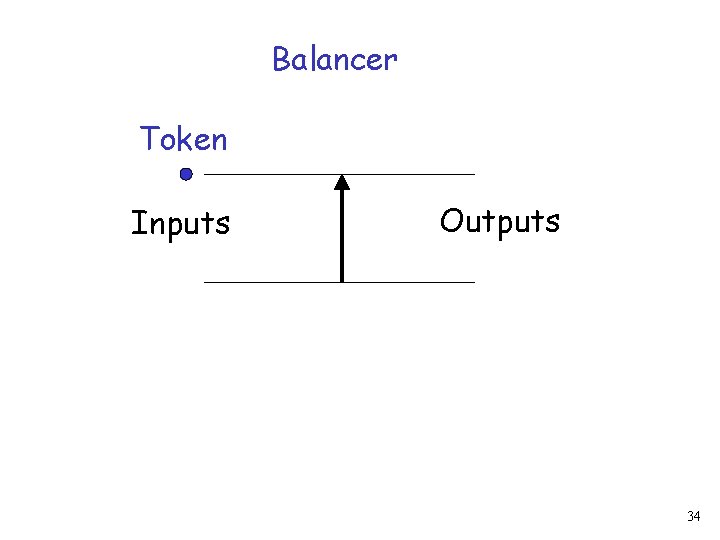
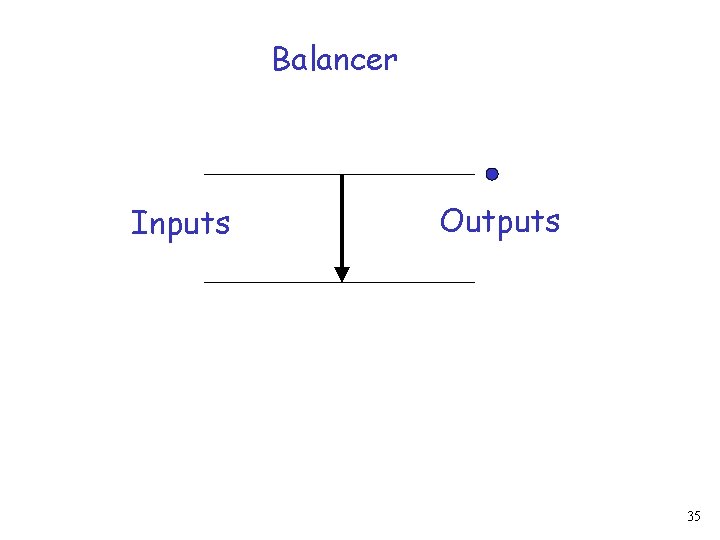
Balancer Token Inputs Outputs 34

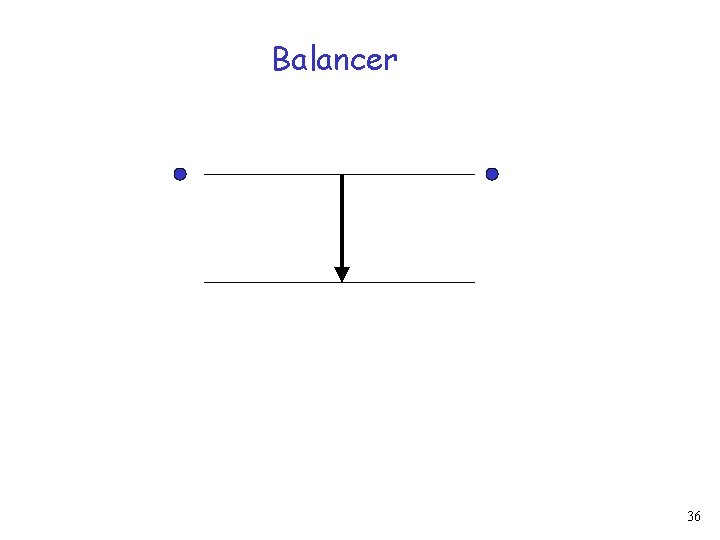
Balancer Inputs Outputs 35

Balancer 36

Balancer 37

Balancer 38

Balancer 39

Balancer 40

Balancer 41

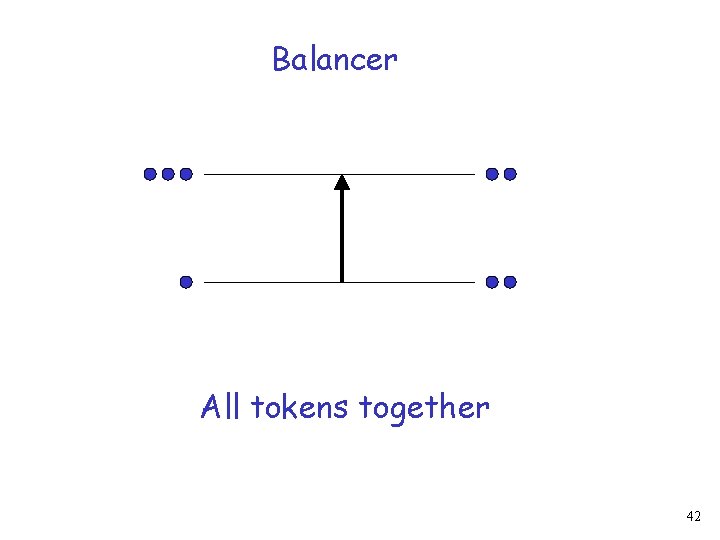
Balancer All tokens together 42

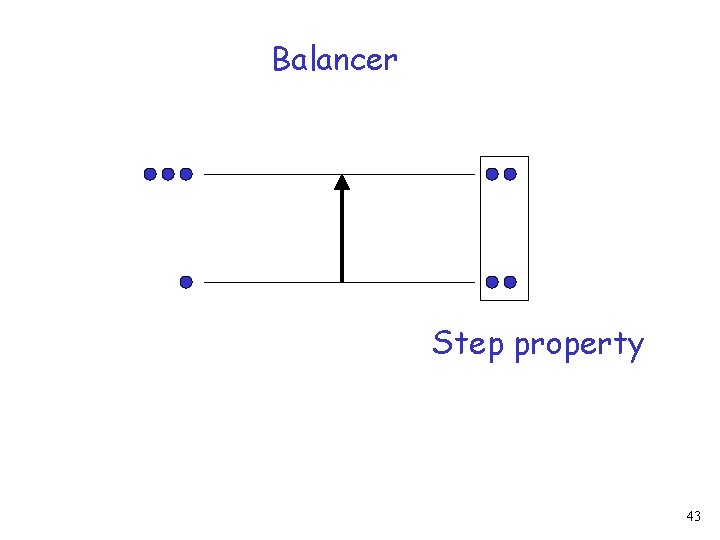
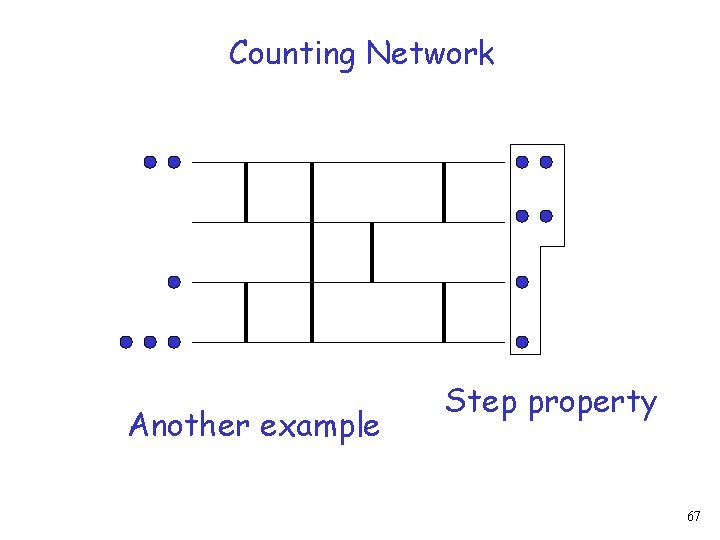
Balancer Step property 43

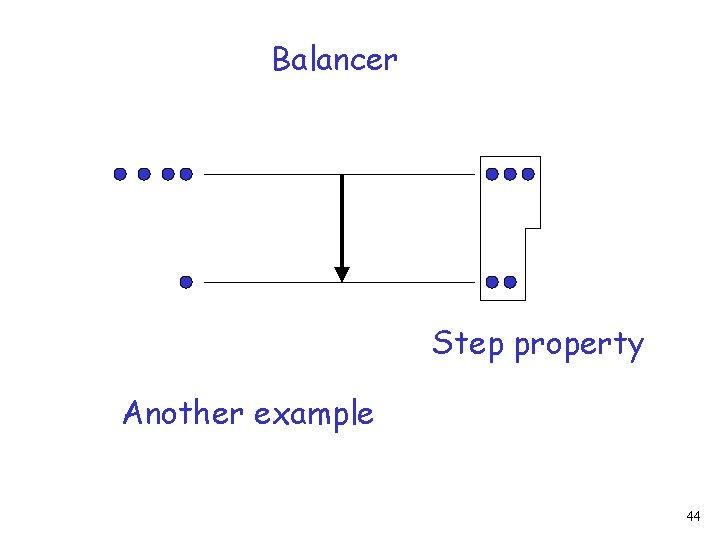
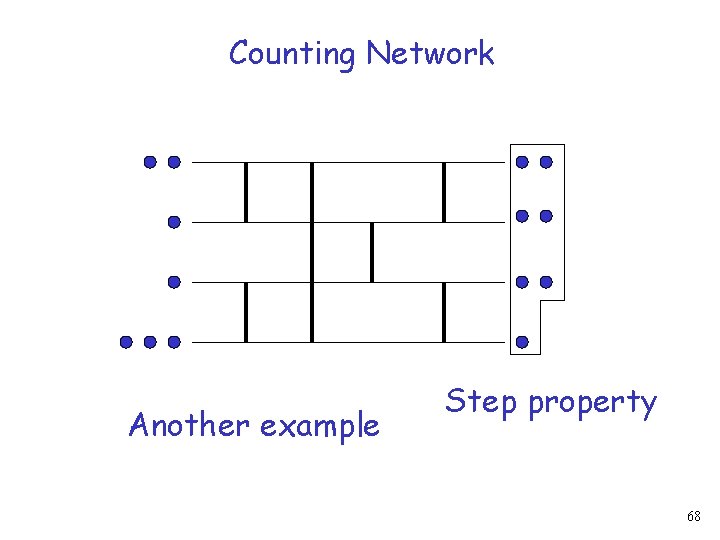
Balancer Step property Another example 44

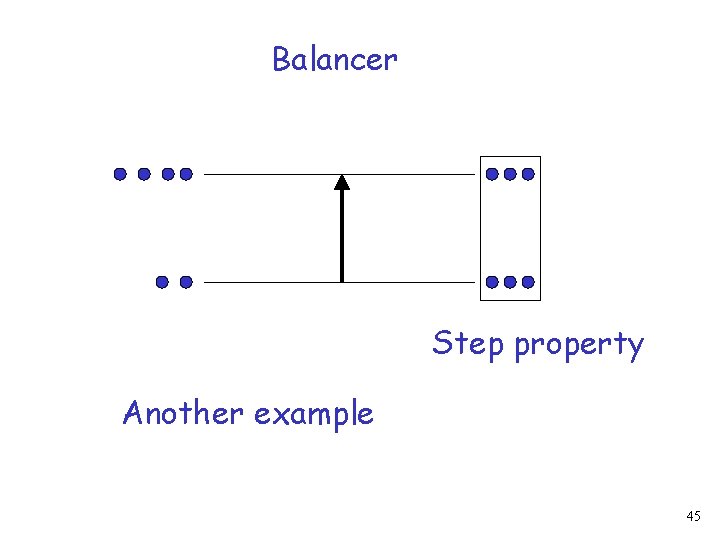
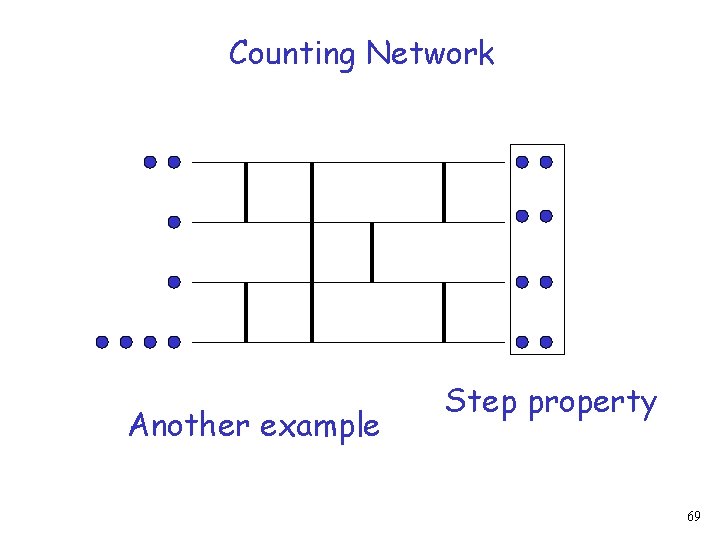
Balancer Step property Another example 45

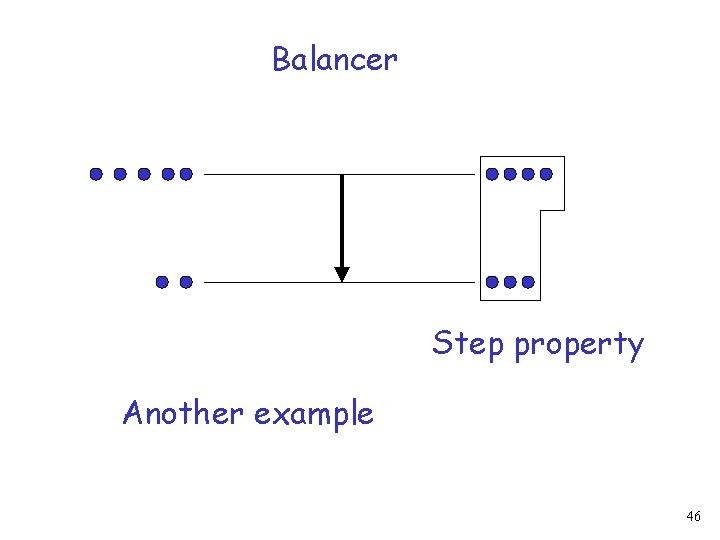
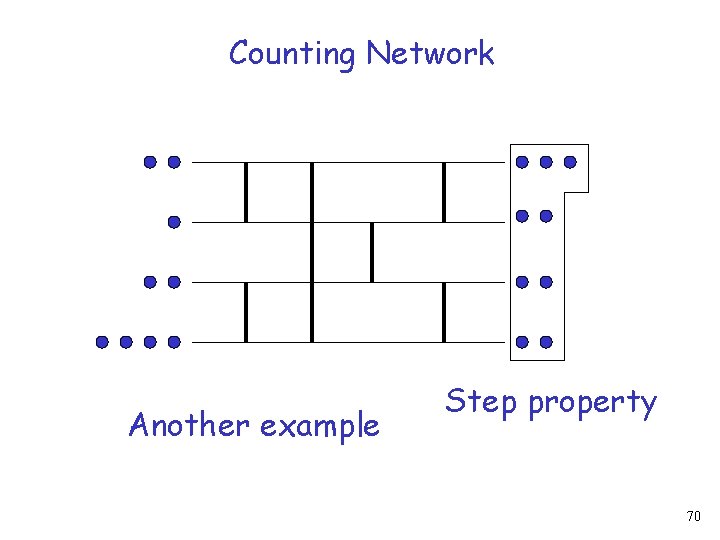
Balancer Step property Another example 46

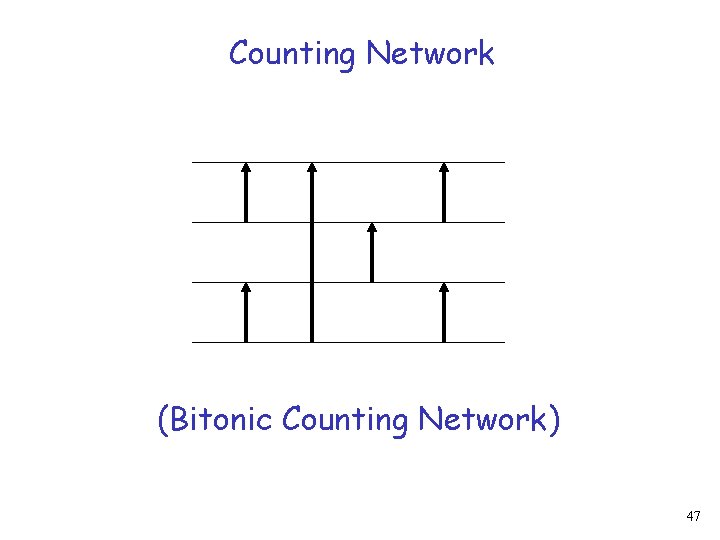
Counting Network (Bitonic Counting Network) 47

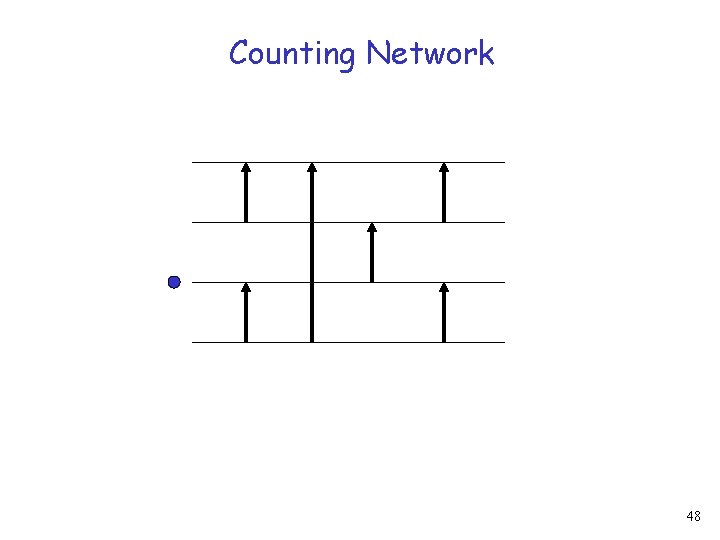
Counting Network 48

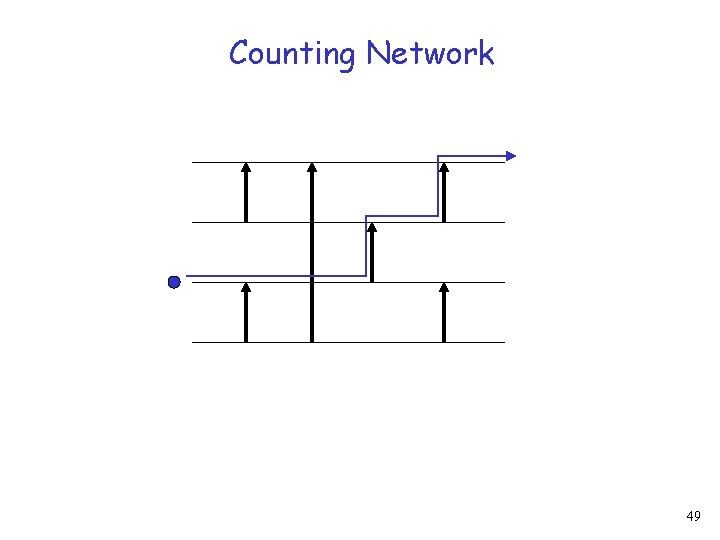
Counting Network 49

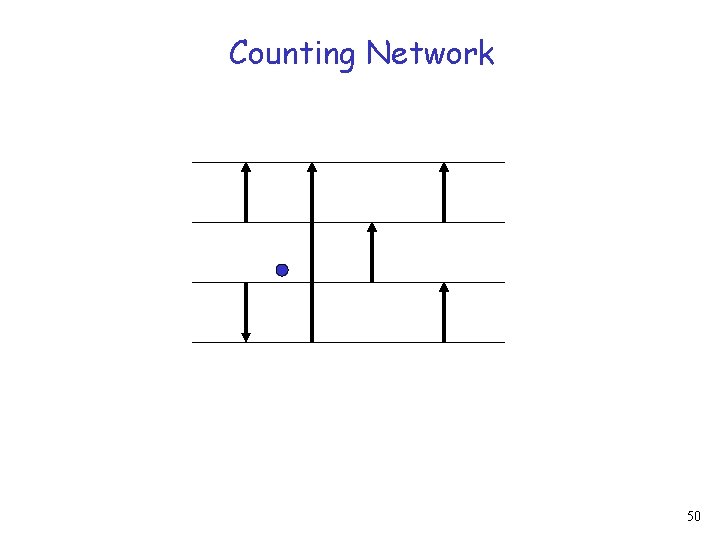
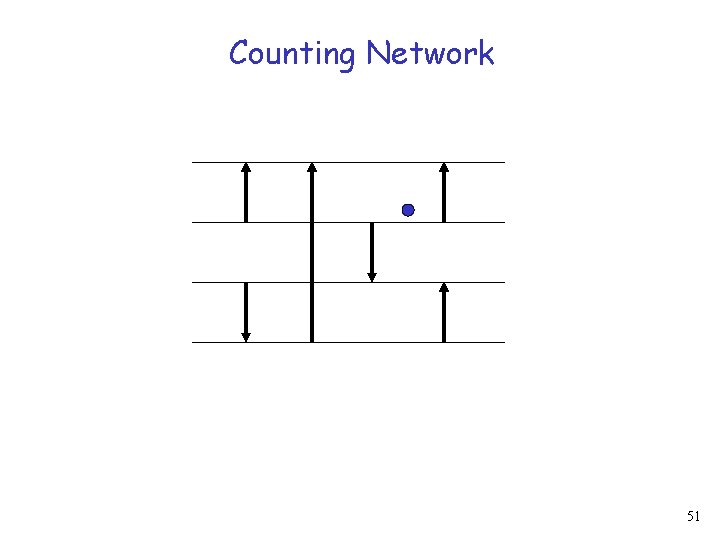
Counting Network 50

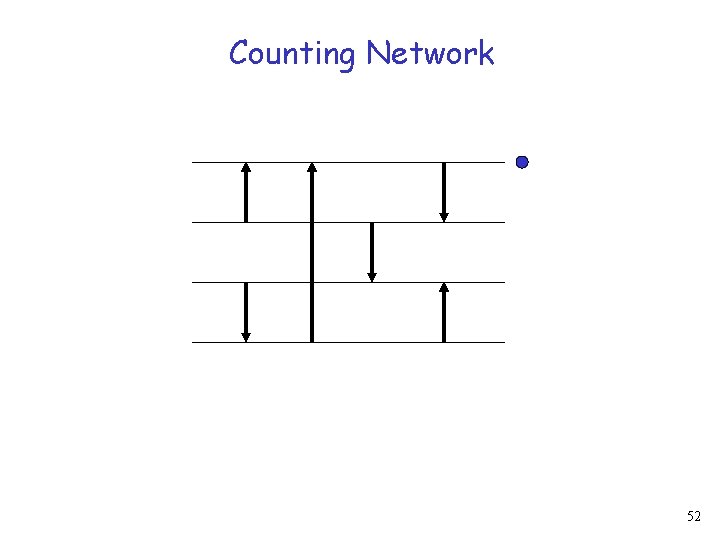
Counting Network 51

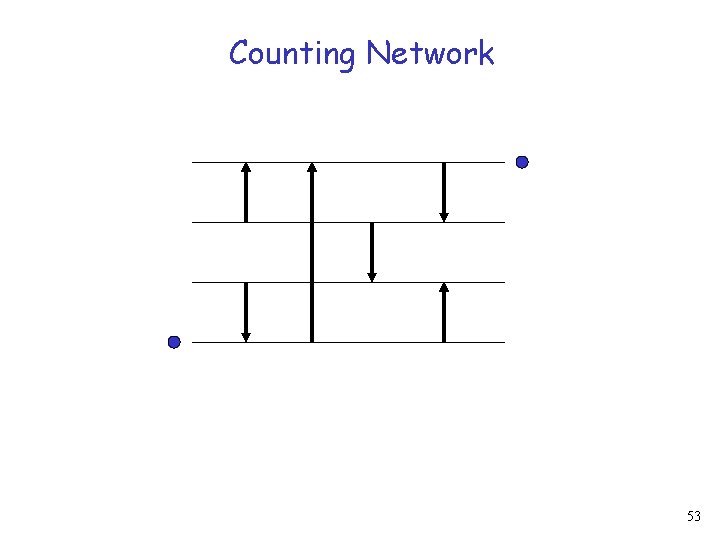
Counting Network 52

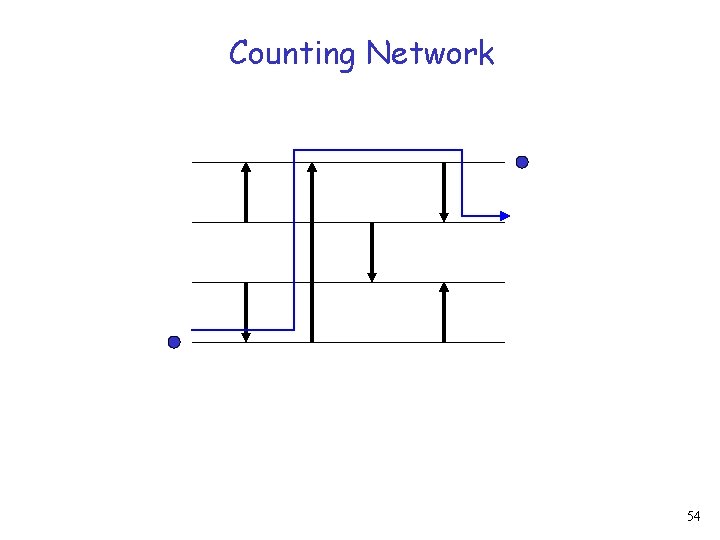
Counting Network 53

Counting Network 54

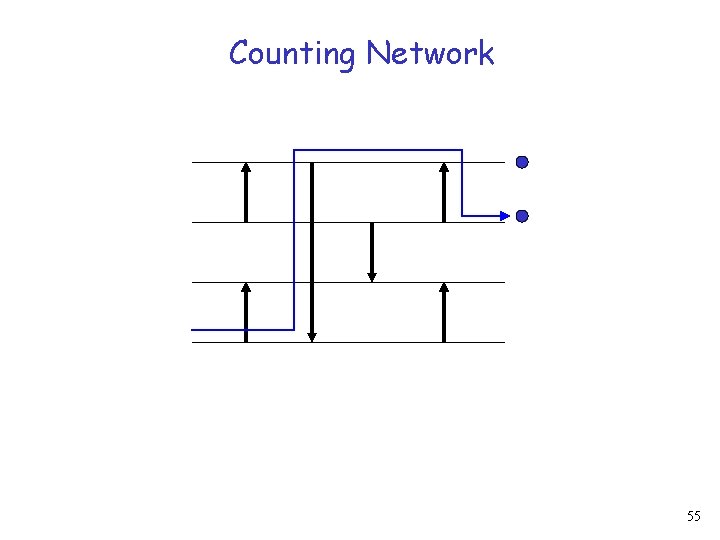
Counting Network 55

Counting Network 56

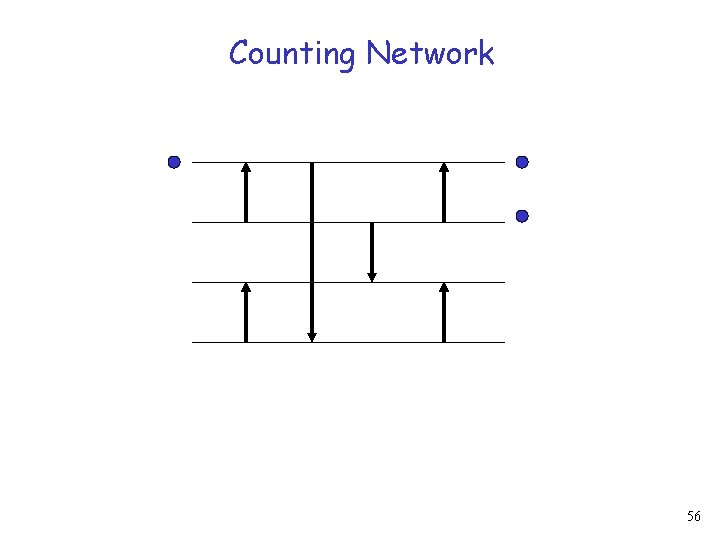
Counting Network 57

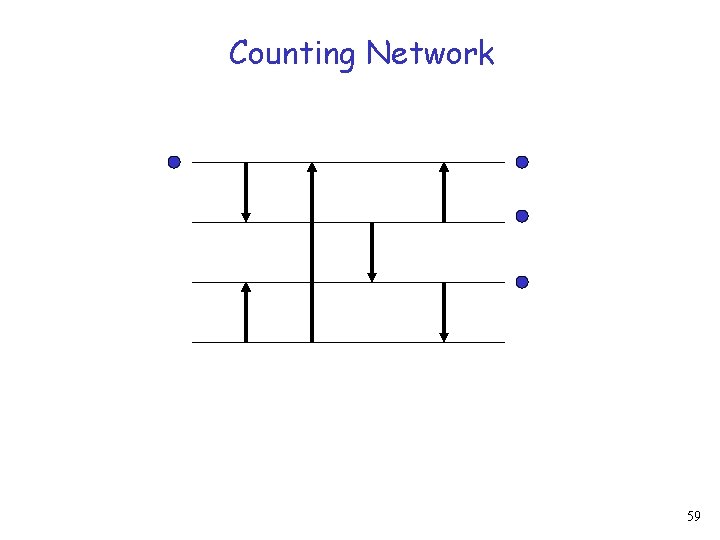
Counting Network 58

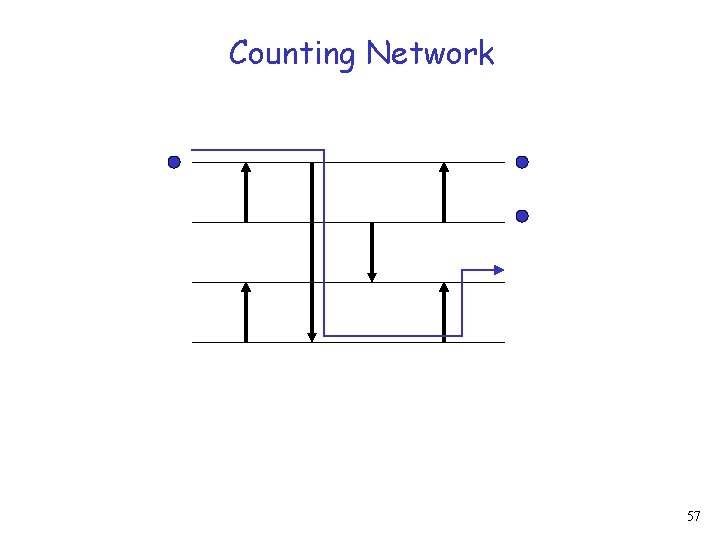
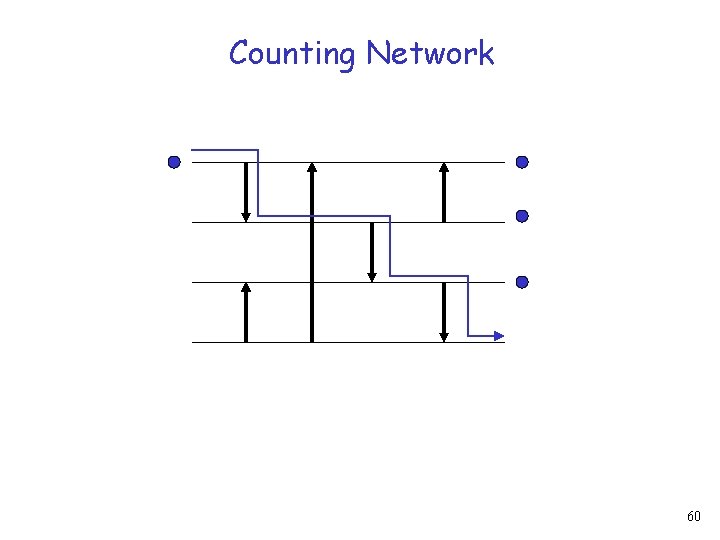
Counting Network 59

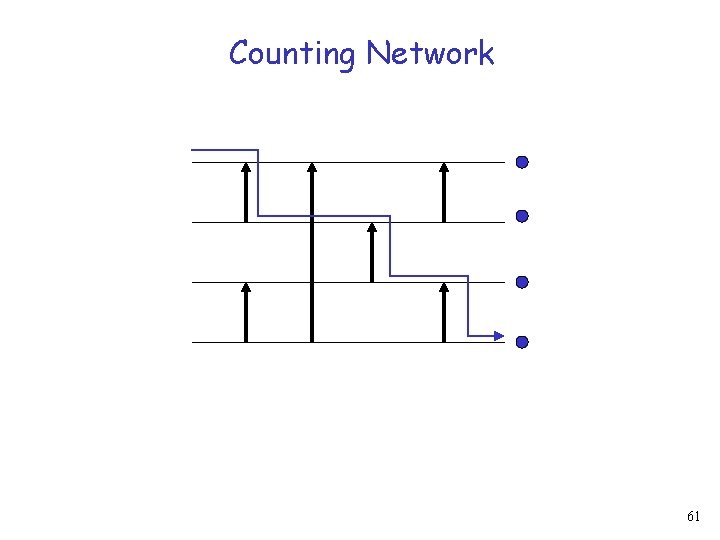
Counting Network 60

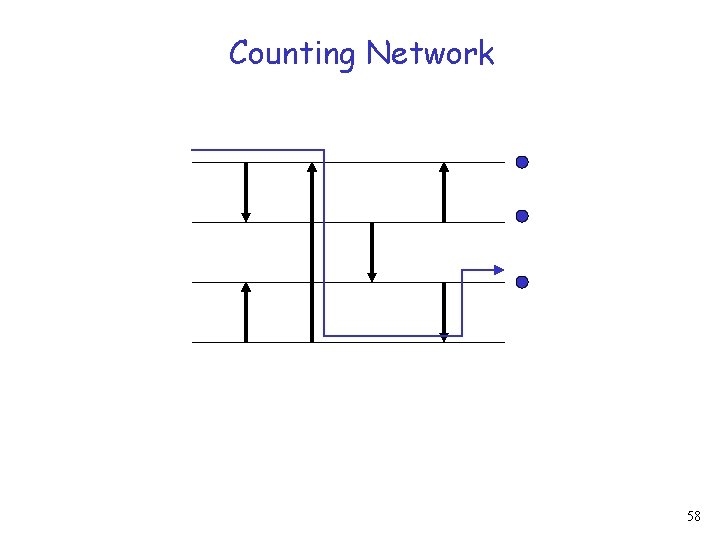
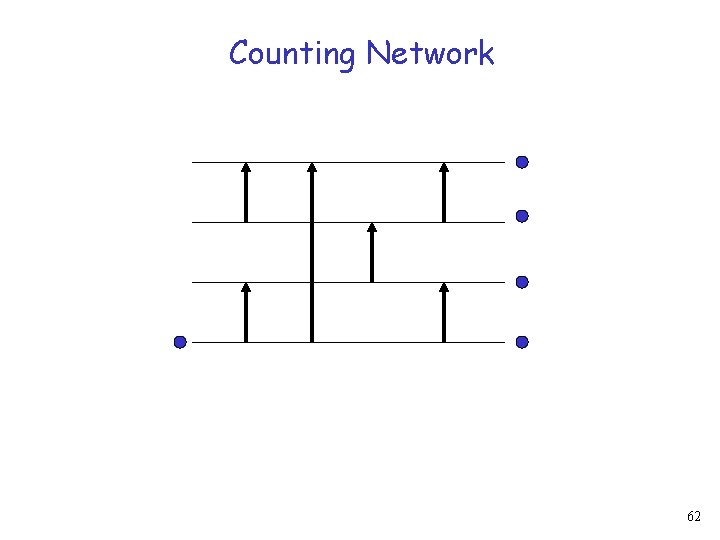
Counting Network 61

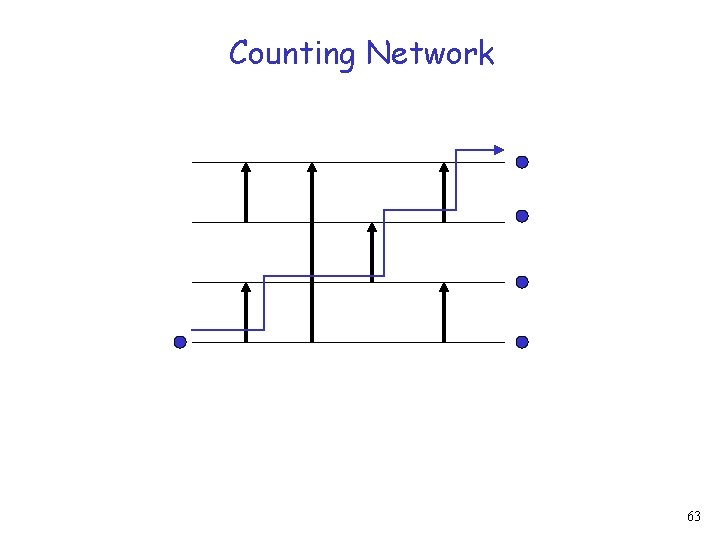
Counting Network 62

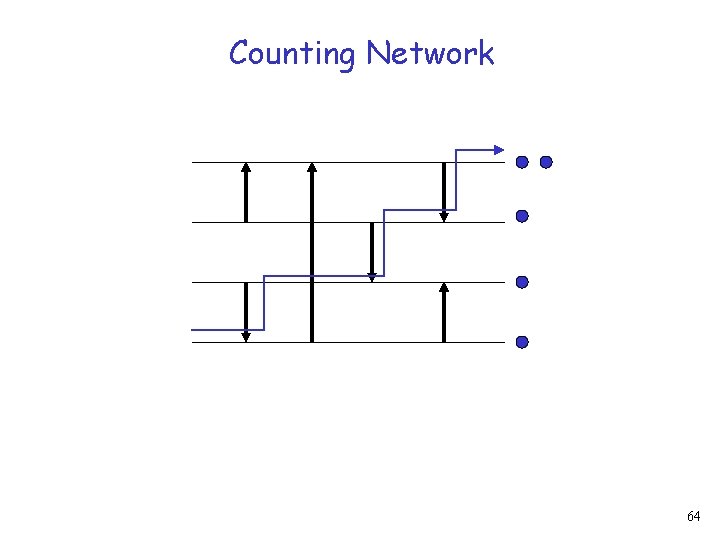
Counting Network 63

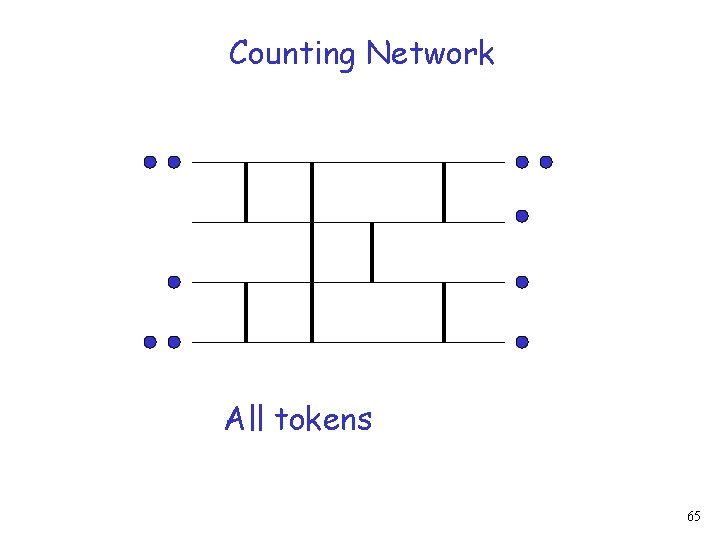
Counting Network 64

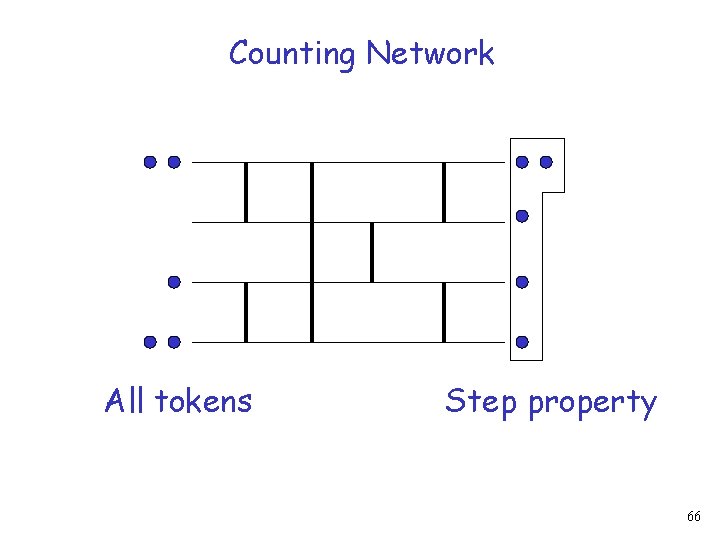
Counting Network All tokens 65

Counting Network All tokens Step property 66

Counting Network Another example Step property 67

Counting Network Another example Step property 68

Counting Network Another example Step property 69

Counting Network Another example Step property 70

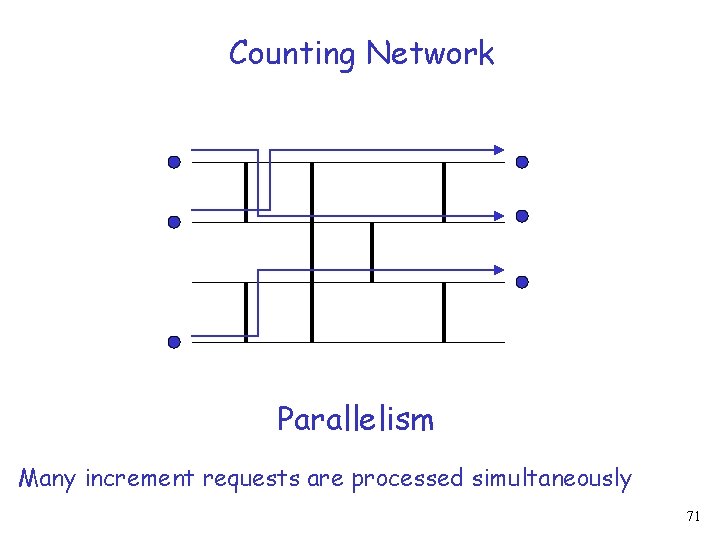
Counting Network Parallelism Many increment requests are processed simultaneously 71

Counting Output Shared variables 0 1 2 3 Token = Increment request 72

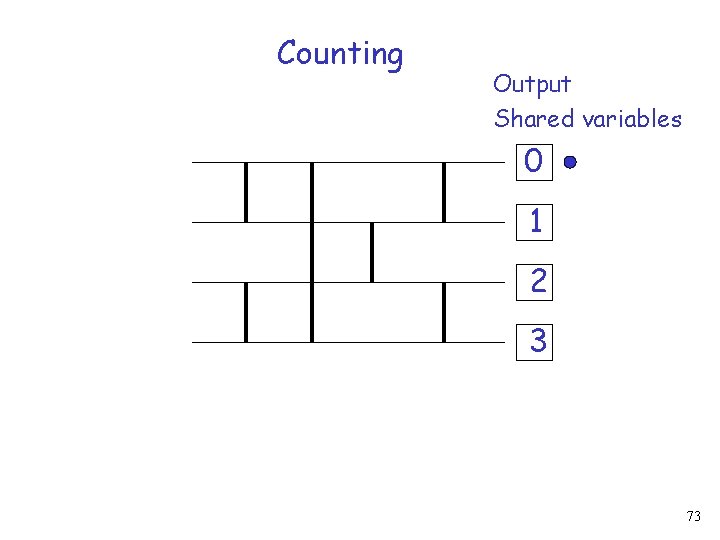
Counting Output Shared variables 0 1 2 3 73

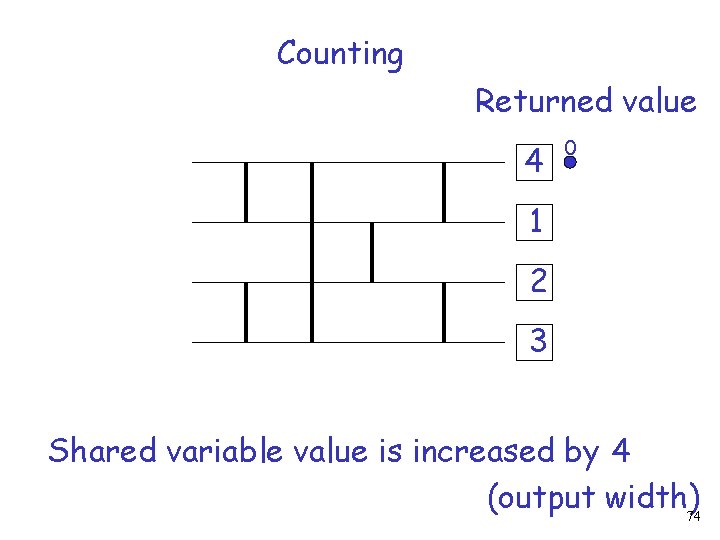
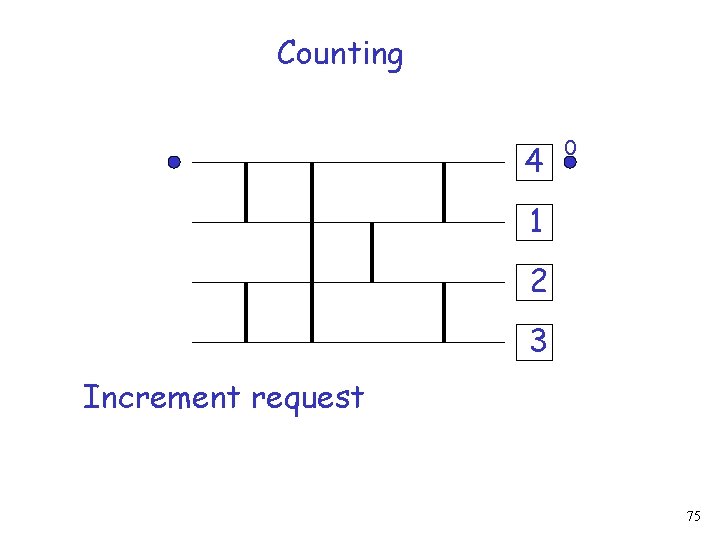
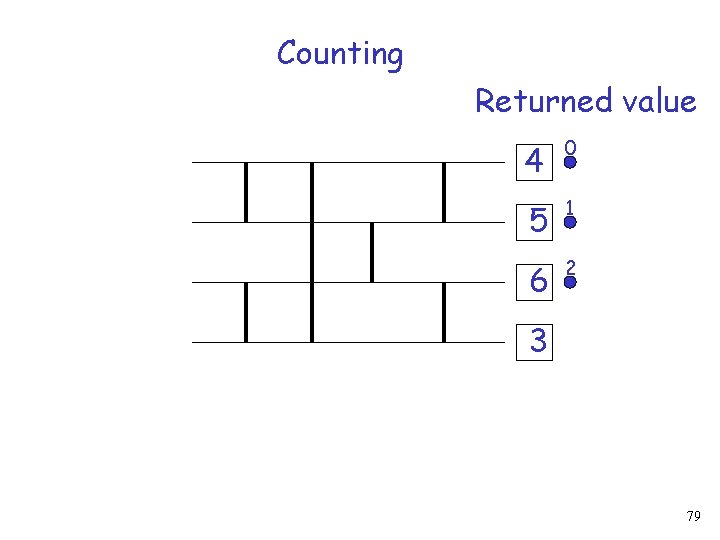
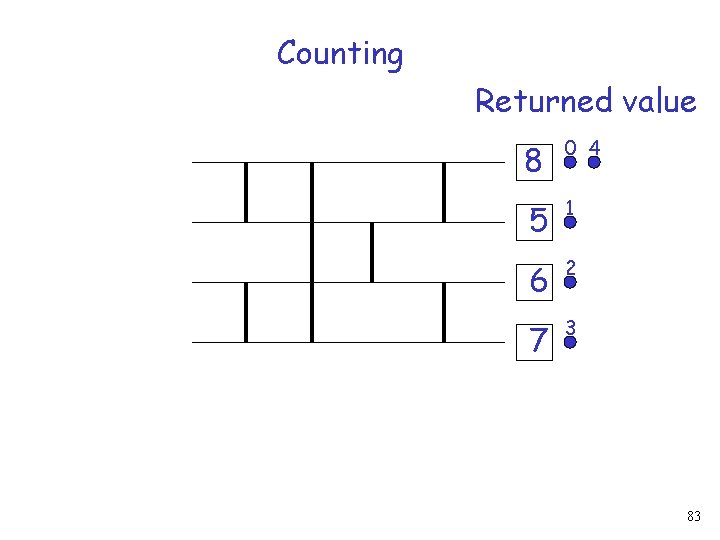
Counting Returned value 4 0 1 2 3 Shared variable value is increased by 4 (output width)74

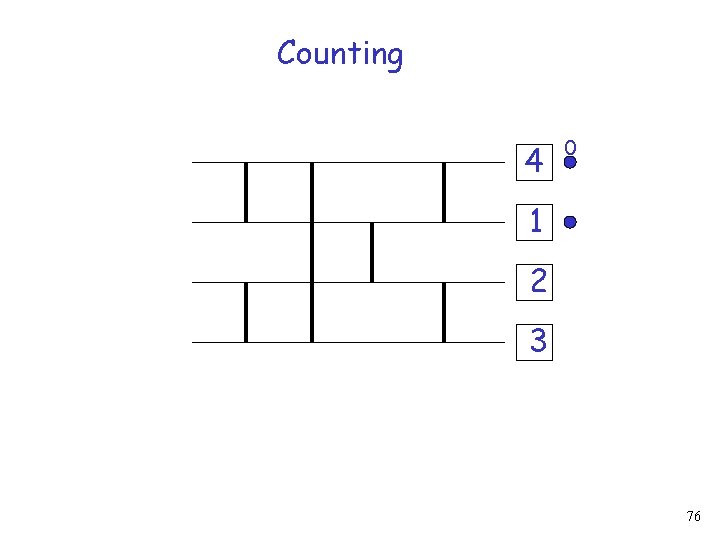
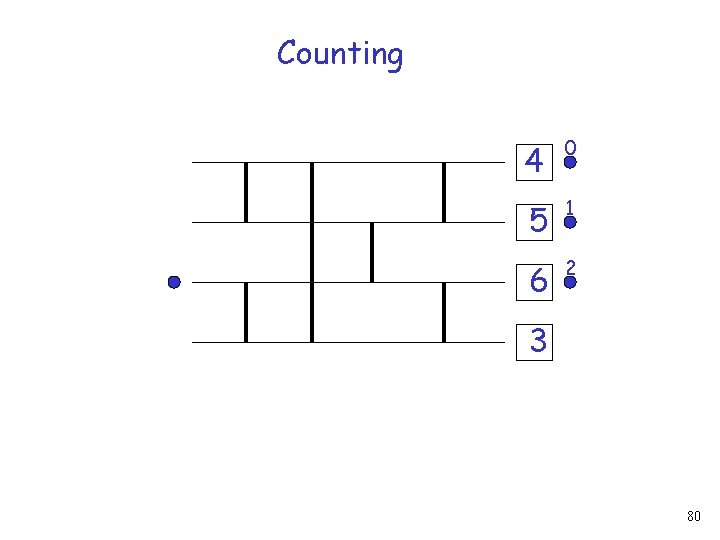
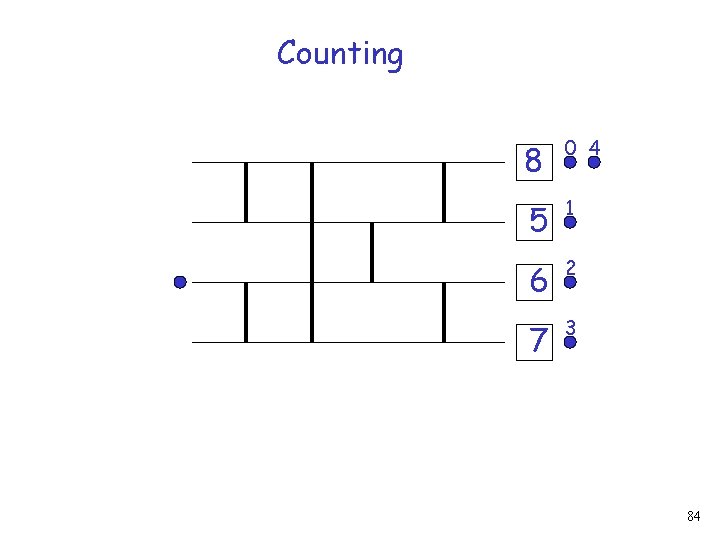
Counting 4 0 1 2 3 Increment request 75

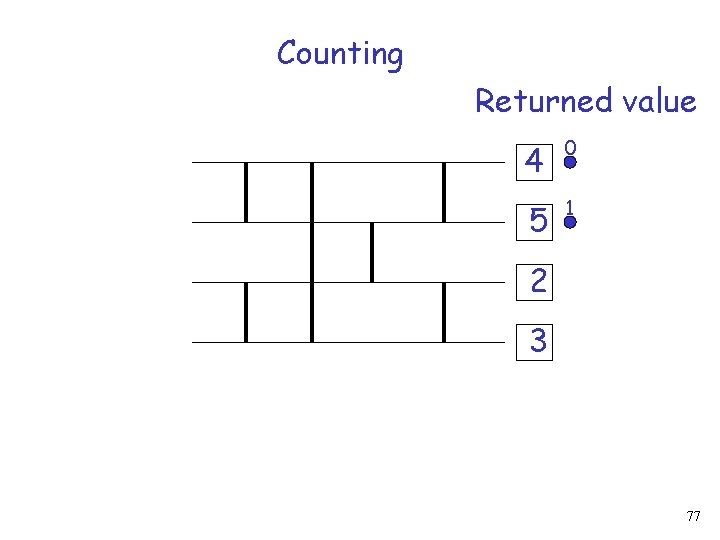
Counting 4 0 1 2 3 76

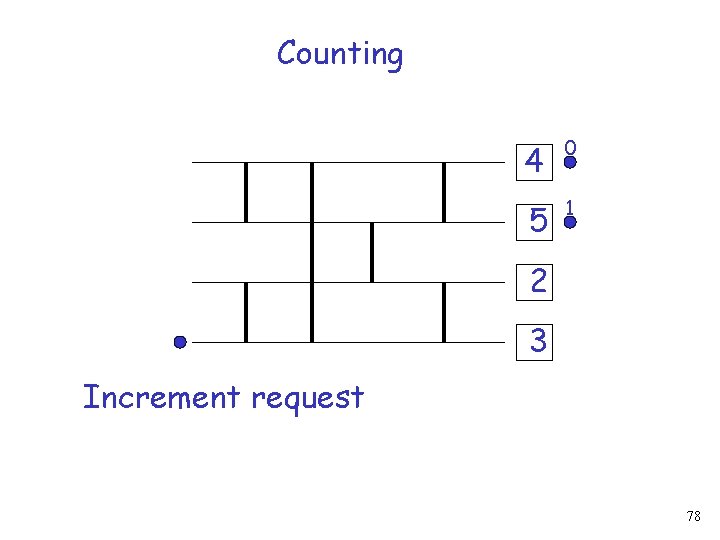
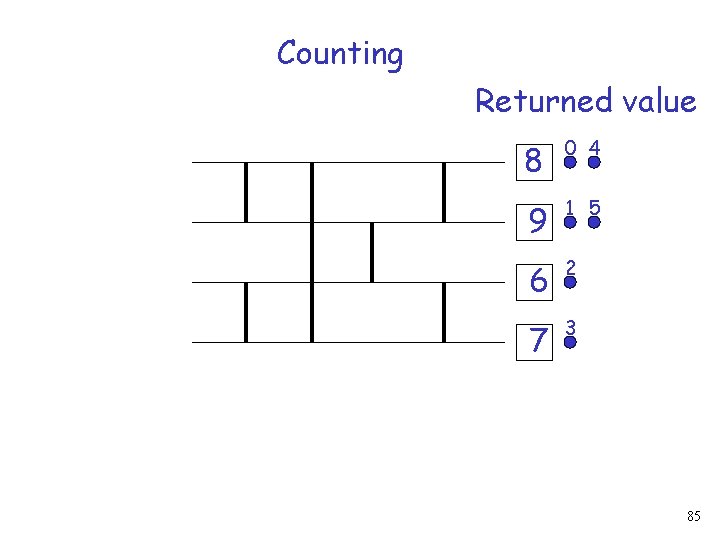
Counting Returned value 4 0 5 1 2 3 77

Counting 4 0 5 1 2 3 Increment request 78

Counting Returned value 4 0 5 1 6 2 3 79

Counting 4 0 5 1 6 2 3 80

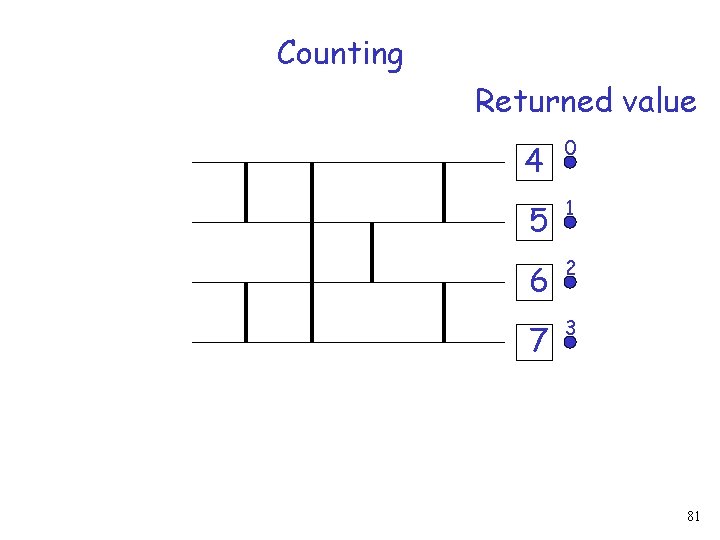
Counting Returned value 4 0 5 1 6 2 7 3 81

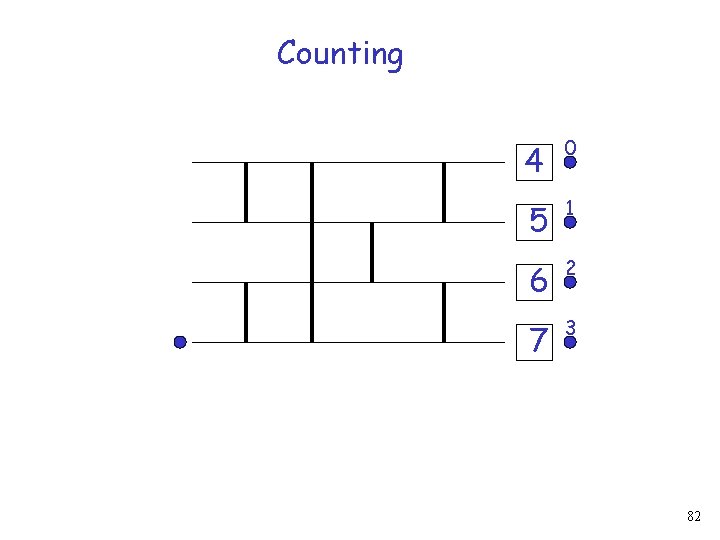
Counting 4 0 5 1 6 2 7 3 82

Counting Returned value 8 0 4 5 1 6 2 7 3 83

Counting 8 0 4 5 1 6 2 7 3 84

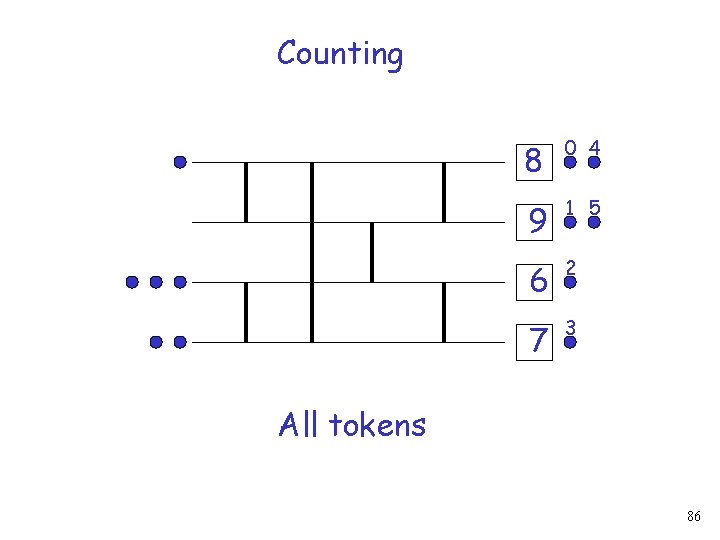
Counting Returned value 8 0 4 9 1 5 6 2 7 3 85

Counting 8 0 4 9 1 5 6 2 7 3 All tokens 86

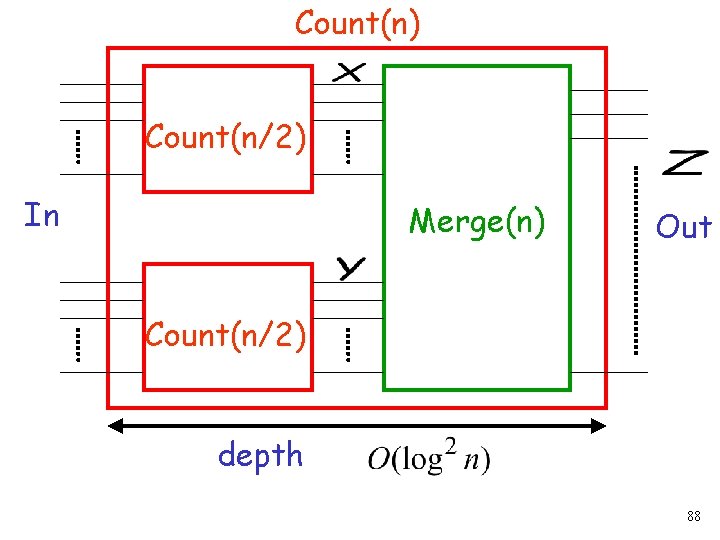
Bitonic Counting Network Isomorphic to Bitonic Sorting Network 87

Count(n) Count(n/2) In Merge(n) Out Count(n/2) depth 88

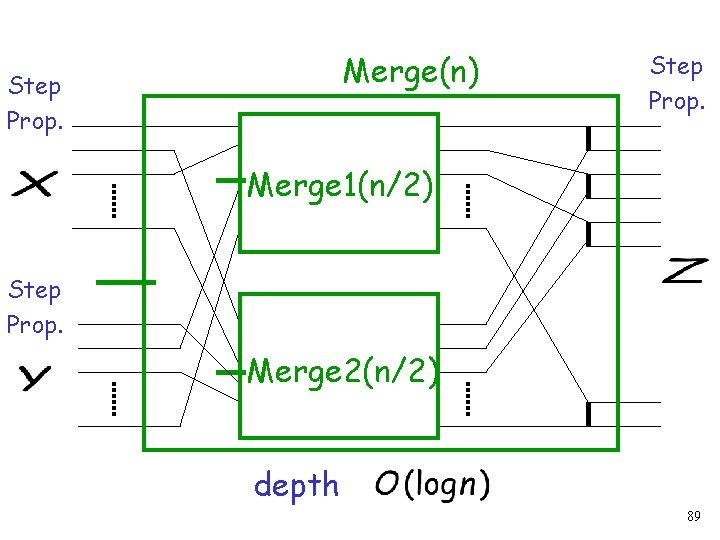
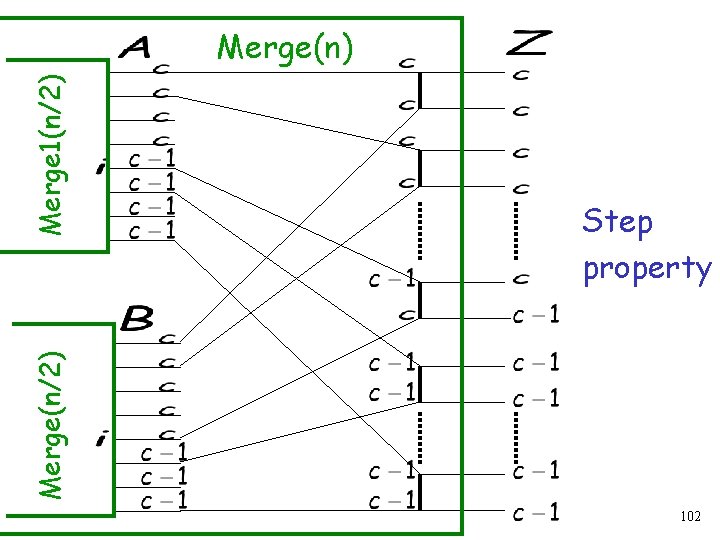
Merge(n) Step Prop. Merge 1(n/2) Step Prop. Merge 2(n/2) depth 89

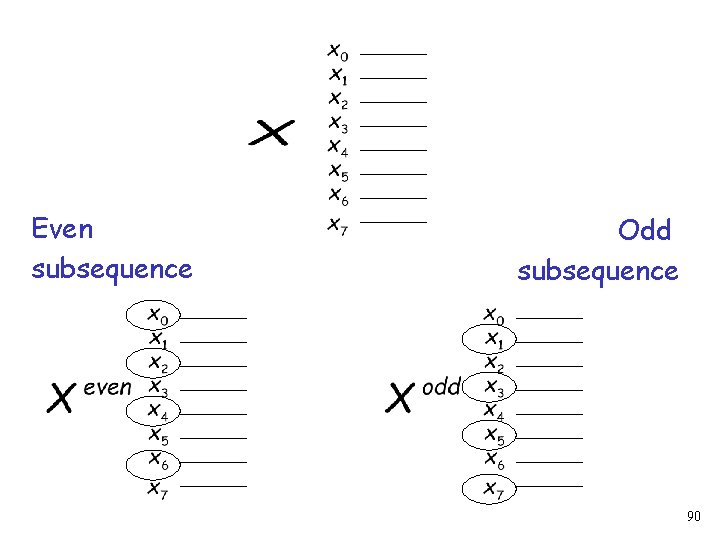
Even subsequence Odd subsequence 90

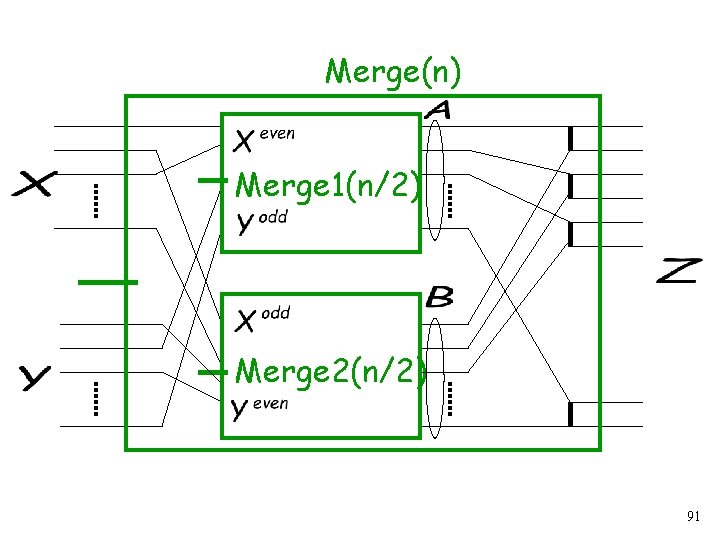
Merge(n) Merge 1(n/2) Merge 2(n/2) 91

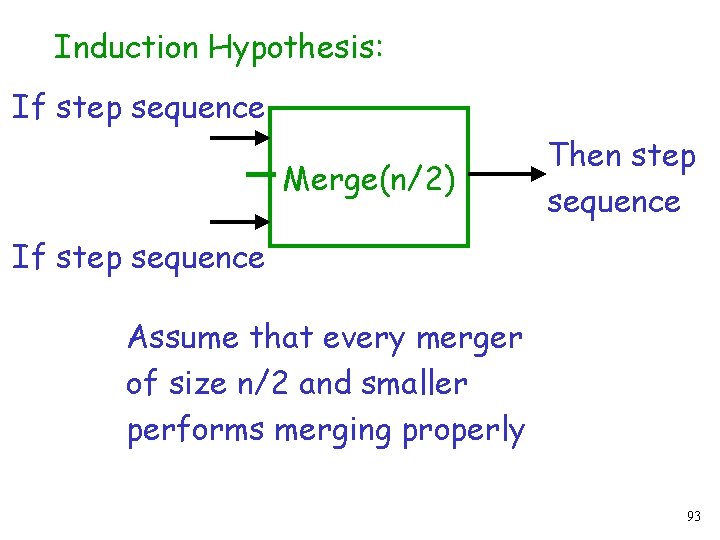
Theorem: The merger(n) produces output Z with step property if both inputs X and Y have step property Proof: The proof is by induction on Induction Basis: For the merger is a balancer and the claim holds trivially. 92

Induction Hypothesis: If step sequence Merge(n/2) Then step sequence If step sequence Assume that every merger of size n/2 and smaller performs merging properly 93

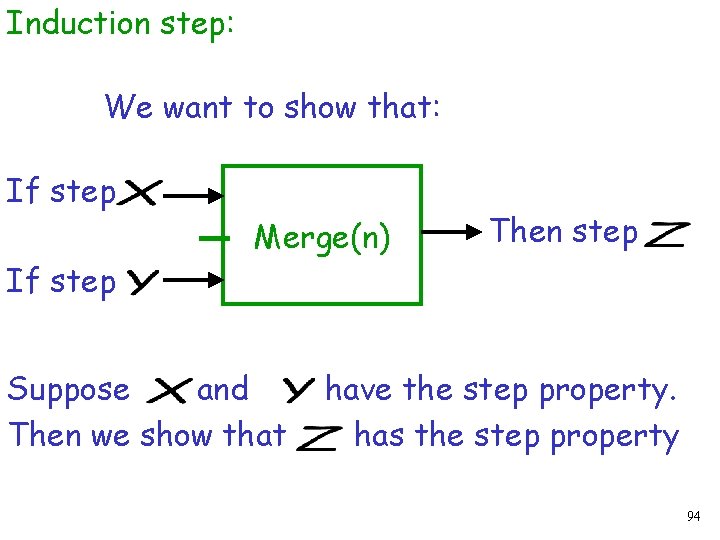
Induction step: We want to show that: If step Merge(n) Suppose and Then we show that Then step have the step property. has the step property 94

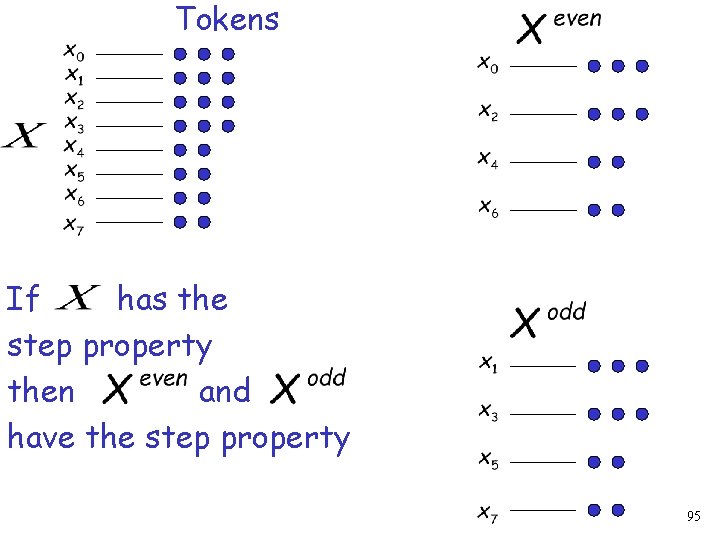
Tokens If has the step property then and have the step property 95

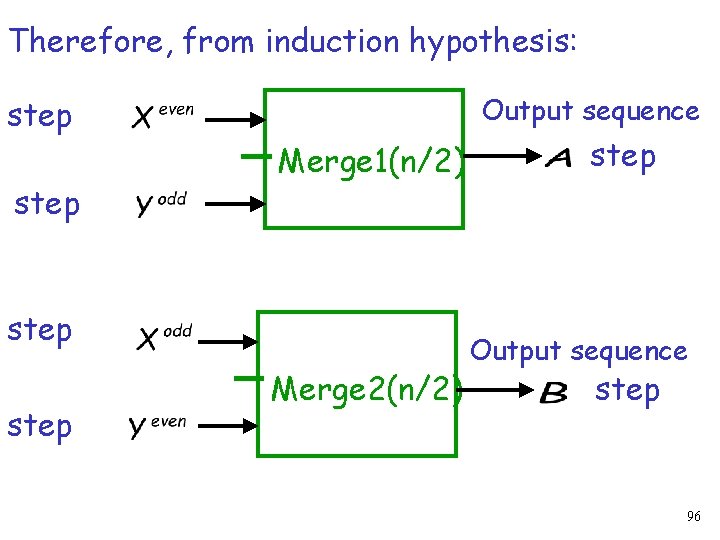
Therefore, from induction hypothesis: Output sequence step Merge 1(n/2) step Merge 2(n/2) step Output sequence step 96

First, we show: Where denotes the total number of tokens in sequence 97
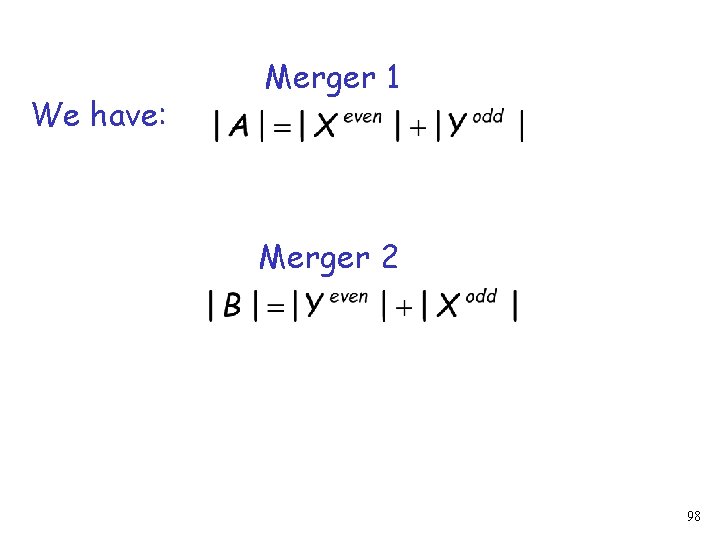
We have: Merger 1 Merger 2 98

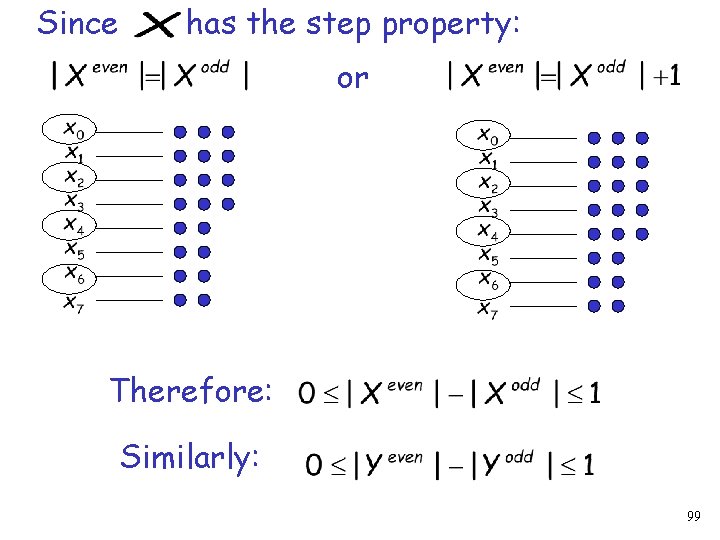
Since has the step property: or Therefore: Similarly: 99
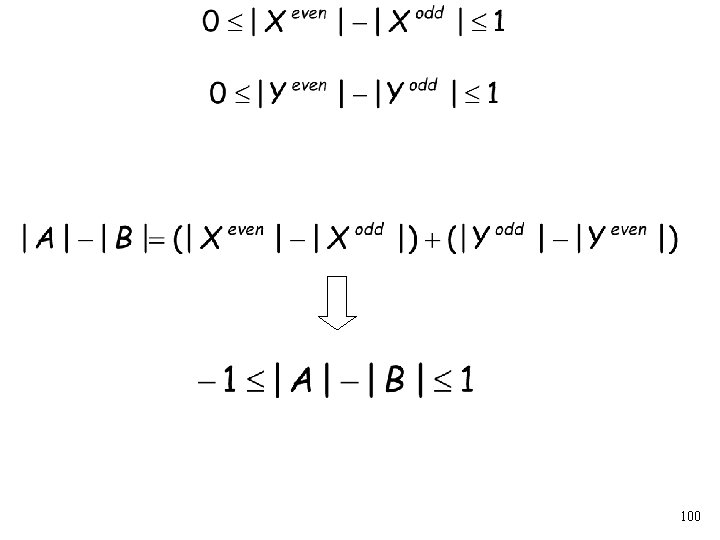
100

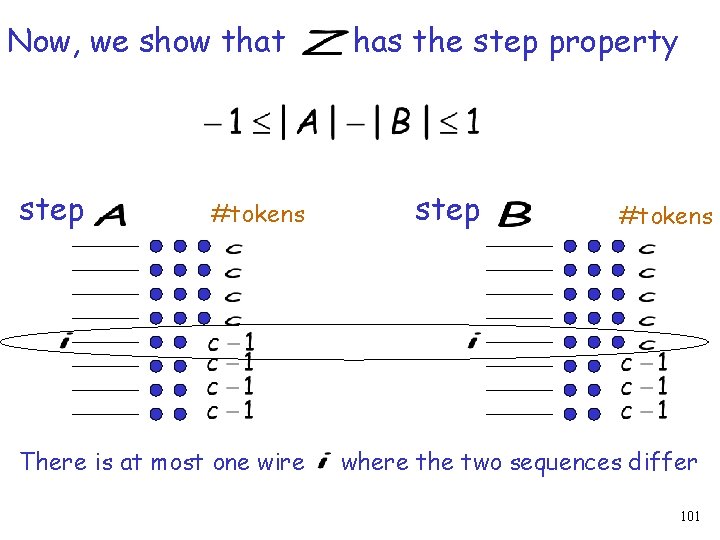
Now, we show that step #tokens There is at most one wire has the step property step #tokens where the two sequences differ 101

Step property Merge(n/2) Merge 1(n/2) Merge(n) 102