Sorting Introduction Assumptions Sorting an array of integers

Sorting

Introduction • Assumptions – Sorting an array of integers – Entire sort can be done in main memory • Straightforward algorithms are O(N 2) • More complex algorithms are O(Nlog. N)

Insertion Sort • • Idea: Start at position 1 and move each element to the left until it is in the correct place At iteration i, the leftmost i elements are in sorted order for i = 1; i < a. size(); i++ tmp = a[i] for j = i; j > 0 && tmp < a[j-1]; j-a[j] = a[j-1] a[j] = tmp

Insertion Sort – Example 34 8 64 51 32 21

Insertion Sort – Analysis • Worst case: Each element is moved all the way to the left – Example input? • Running time in this case?

Insertion Sort – Analysis • Running time in this case? – inner loop test executes p+1 times for each p N Σ i = 2 + 3 + 4 + … + N = θ(N 2) i=2

Sorting – Lower Bound • Inversion – an ordered pair (i, j) where i < j but a[i] > a[j] – Number of swaps required by insertion sort – Running time of insertion sort O(I+N) • Calculate average running time of insertion sort by computing average number of inversions

Sorting – Lower Bound • Theorem 7. 1: The average number of inversions in an array of N distinct elements is N(N-1)/4 • Proof: Total number of inversions in a list L and its reverse Lr is N(N-1)/2. Average list has half this amount, N(N-1)/4. • Insertion sort is O(N 2) on average

Sorting – Lower Bound • Theorem 7. 2: Any algorithm that sorts by exchanging adjacent elements requires Ω(N 2) time on average. • Proof: Number of inversions is N(N-1)/4. Each swap removes only 1 inversion, so Ω(N 2) swaps are required.

Shellsort • Idea: Use increment sequence h 1, h 2, …ht. After phase using increment hk, a[i] <= a[i+ hk] for each hk for i = hk to a. size() tmp = a[i] for j = i j >= hk && tmp < a[j- hk] j-= hk a[j] = a[j- hk ] a[j] = tmp

Shellsort • Conceptually, separate array into hk columns and sort each column • Example: 81 94 11 96 12 35 17 95 28 58 41 75 15

Shellsort: Analysis • Increment sequence determines running time • Shell’s increments – ht = floor(N/2) and hk=floor(hk+1/2) – θ(N 2) • Hibbard’s increments – 1, 3, 7, …, 2 k-1 – θ(N 3/2)

Shellsort – Analysis • Theorem 7. 3: The worst-case running time of Shellsort, using Shell’s increments, is θ(N 2). • Proof – part 1: There exists some input that takes Ω(N 2). Choose N to be a power of 2. All increments except last will be even. Give as input array with N/2 largest numbers in even positions and N/2 smallest in odd positions.

Shellsort – Analysis Example: 1 9 2 10 3 11 4 12 5 13 6 14 7 15 8 16 • At last pass, ith smallest number will be in position 2 i-1 requiring i-1 moves. Total number of moves: N/2 Σ i-1 = Ω(N 2) i=1

Shellsort – Analysis • Proof – part 2: A pass with increment hk performs hk insertion sorts of lists of N/hk elements. Total cost of a pass is O(hk(N/ hk)2) = O(N 2/ hk). Summing over all passes gives a total bound of O(sum from 1 -t(N 2/hi)) = O(N 2 (sum from 1 -t 1/hi) = O(N 2)

Heapsort • Strategy – Apply build. Heap function – Perform N delete. Min operations • Running time is O(Nlog. N) • Problem: Simplementation uses two arrays – N extra space

Heapsort • Solution: After deletion, size of heap shrinks by 1, so simply insert into empty slot • Problem: Results in array sorted in decreasing order – use max heap instead • Example: 97 53 59 26 41 58 31

Mergesort • Recursively sort elements 1 -N/2 and N/2 -N and merge the result • This is a classic divide-and-conquer algorithm. • Uses temporary array – extra space

Mergesort – Algorithm • Base case – List of 1 element, return • Otherwise – Mergesort left half – Mergesort right half – Merge

Mergesort – Algorithm • Merge left. Pos = left. Start; right. Pos = right. Start; tmp. Pos = tmp. Start; while(left. Pos <=left. End && right. Pos <= right. End) if(a[left. Pos] <= a[right. Pos]) tmp. Array[tmp. Pos++] = a[left. Pos++] else tmp. Array[tmp. Pos++] = a[right. Pos++] //copy rest of left half //copy rest of right half //copy tmp. Array back • Example 24 13 26 1 2 27 38 15

Mergesort – Analysis • • T(1) = 1 T(N) = 2 T(N/2) + N – divide by N T(N)/N = T(N/2)/N/2 + 1 – substitute N/2 T(N/2)/N/2 = T(N/4)/N/4 + 1 T(N/4)/N/4 = T(N/8)/N/8 + 1 … T(2)/2 = T(1)/1 + 1 – telescoping T(N)/N = T(1)/1 + log. N – mult by N T(N) = N + Nlog. N = O(Nlog. N) • Can also repeatedly substitute recurrence on right-hand side

Quicksort • Base case: Return if number of elements is 0 or 1 • Pick pivot v in S. • Partition into two subgroups. First subgroup is < v and last subgroup is > v. • Recursively quicksort first subgroup and last subgroup

Quicksort • Picking the pivot – Choose first element • Bad for presorted data – Choose randomly • Random number generation can be expensive – Median-of-three • Choose median of left, right, and center • Good choice!

Quicksort • Partitioning – Move pivot to end – i = start; j = end; – i++ and j-- until a[i] > pivot and a[j] < pivot and i<j • swap a[i] and a[j] – swap a[last] and a[i] //move pivot • Example 13 81 92 43 65 31 57 26 75 0

Quicksort – Analysis • Quicksort relation – T(N) = T(i) + T(N-i-1) + c. N • Worst-case – pivot always smallest element – – – T(N) = T(N-1) + c. N T(N-1) = T(N-2) + c(N-1) T(N-2) = T(N-3) + c(N-2) T(2) = T(1) + c(2) – add previous equations T(N) = T(1) + csum([2 -N] of i) = O(N 2)

Quicksort – Analysis • Best-case – pivot always middle element – T(N) = 2 T(N/2) + c. N – Can use same analysis as mergesort – = O(Nlog. N) • Average-case (pg 278) – = O(Nlog. N)

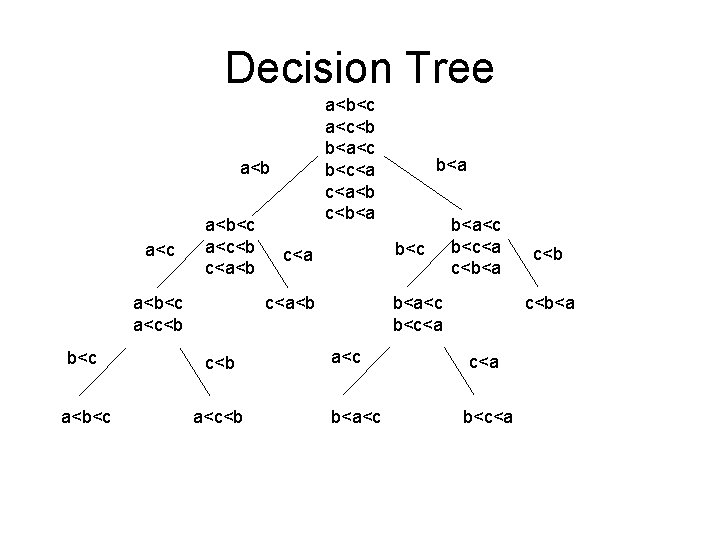
Sorting – Lower Bound • A sorting algorithm that uses comparisons requires ceil(log(N!)) in worst case and log(N!) on average.

Decision Tree a<b<c a<c<b b<a<c b<c<a c<a<b c<b<a a<b a<c a<b<c a<c<b c<a<b a<b<c a<c<b b<c c<a<b b<c c<b a<b<c a<c<b b<a<c b<c<a c<b<a b<a<c b<c<a a<c b<a<c c<b<a c<a b<c<a

Sorting – Lower Bound • Let T be a binary tree of depth d. The T has at most 2 d leaves. • A binary tree with L leaves must have depth at least ceil(log L). • Any sorting algorithm that uses only comparisons between elements requires at least ceil(log(N!)) comparisons in the worst case. – N! leaves because N! permutations of N elements

Sorting – Lower Bound • Any sorting algorithm that uses only comparisons between elements requires Ω(Nlog. N) comparisons • log(N!) comparisons are required • log(N!) = log(N(N-1)(N-2)…(2)(1)) • = log. N+log(N-1)+log(N-2)+…+log 1 • >= log. N+log(N-1)+log(N-2)+…+log. N/2 • >= N/2 log(N/2) >= N/2 log(N)-N/2 • = Ω(Nlog. N)

Bucketsort • Sorting algorithm that runs in O(N) time, how? What is special about this algorithm? for i = 1 to n increment count[Ai]