Sorting Intro 2 CS week 7 1 Why

Sorting Intro 2 CS – week 7 1

Why Study Sorting? • Sorting lists is useful • A way to examine algorithms and learn how to analyze them. • Some techniques can be used in other problems. 2

Permuting a list • How many basic computational operations? • Could we do it with less? 3

Counting operations • 4

Counting operations n t im es • 5

Counting operations n t im es So (for now) we will focus mostly on how many times the loops run, and basic operations that execute many times We will also mostly care about running time on “large enough” input sizes. This is also where we feel running times the most. 6

Search • How many basic operations needed? • The loop executes up to n times. • The “best-case”: we stop after one iteration • The “worst-case”: we stop after n iterations • The “average case”? • Can we do better? 7

Binary Search • On a sorted list, we can search faster. item Compare V If item found, we are done! Otherwise we can narrow the search: If item > V: If item < V: X X X X 8

Binary Search 9

Example Search for ‘e’ middle bottom ‘a’ ‘b’ ‘c’ ‘d’ ‘e’ 0 1 2 3 4 ‘f’ 5 ‘g’ ‘h’ 6 7 top ‘i' 8 ‘j’ 9 ‘k’ ‘l’ ‘m’ ‘n’ ‘o’ 10 11 12 13 14 10

Example Search for ‘e’ bottom middle ‘a’ ‘b’ ‘c’ ‘d’ ‘e’ 0 1 2 3 4 top ‘f’ 5 ‘g’ ‘h’ 6 7 ‘i' 8 ‘j’ 9 ‘k’ ‘l’ ‘m’ ‘n’ ‘o’ 10 11 12 13 14 11

Example Search for ‘e’ bottom mid top ‘a’ ‘b’ ‘c’ ‘d’ ‘e’ 0 1 2 3 4 ‘f’ 5 ‘g’ ‘h’ 6 7 ‘i' 8 ‘j’ 9 ‘k’ ‘l’ ‘m’ ‘n’ ‘o’ 10 11 12 13 14 12

Example Search for ‘e’ top middle bottom ‘a’ ‘b’ ‘c’ ‘d’ ‘e’ 0 1 2 3 4 ‘f’ 5 ‘g’ ‘h’ 6 7 ‘i' 8 ‘j’ 9 ‘k’ ‘l’ ‘m’ ‘n’ ‘o’ 10 11 12 13 14 13

Binary Search • 14

Is this much better? • 15

Sorting a list A simple idea. • Find the largest value in the list. • Swap it into the last cell. • Find the largest value in the first n-1 cells, • swap it into the (n-1)th cell, • Repeat for smaller and smaller lists until done… 16

Max Sort (AKA Selection Sort) 17

Max Sort 18

Max Sort • 19

Max Sort • 20

Quick. Sort • 3 8 1 0 5 9 4 2 6 7 3 2 1 0 5 4 6 8 7 9 21

Quick Sort 22

Quick Sort 23

Partition (example) First, pivot is swapped to the end 3 8 1 0 5 9 4 6 7 2 e s 3 8 1 0 5 9 4 2 7 6 s e 3 2 1 0 5 9 4 8 7 6 24

Partition (example cont. ) s e 3 2 1 0 5 9 4 8 7 6 se 3 2 1 0 5 4 9 8 7 6 Finally, pivot is swapped back into its place se 3 2 1 0 5 4 6 8 7 9 25

Example Original list: m a c k h l i b j f d e g o n b a c d h l i m j f n e g o k a b c d h g i e f j n m l o k a b c d e f g h i j n m l k o a b c d e f g h i j k m l n o a b c d e f g h i j k l m n o 26

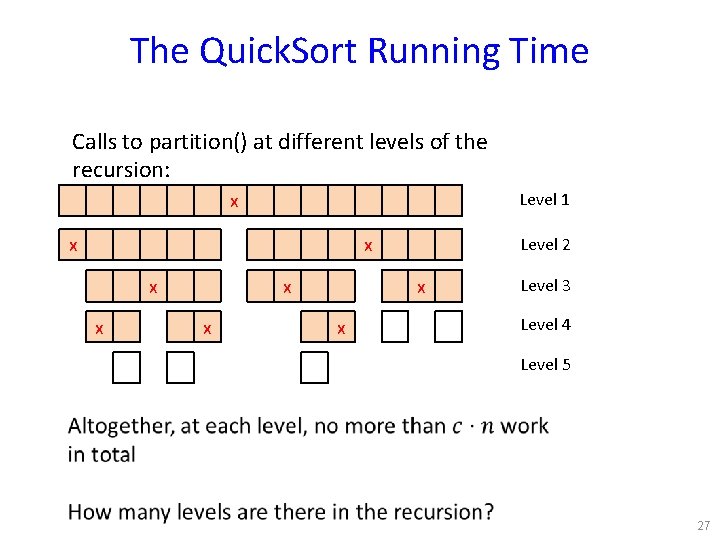
The Quick. Sort Running Time Calls to partition() at different levels of the recursion: x Level 1 x x x Level 2 x x Level 3 Level 4 Level 5 27

The Best Case The Pivot at each level is exactly the median value. x Level 1 x x x Level 2 x Level 3 Level 4 28

The Worst Case The Pivot at each level is an extreme value (smallest or largest). x Level 1 x Level 2 x Level 3 x Level 4 … 29

The Average Case The average case is much closer to the best case than to the worst case. x Level 1 x x x Level 2 x x Level 3 Level 4 Level 5 30

Sorting Lower Bound • 31

Sorting Lower Bound • 32

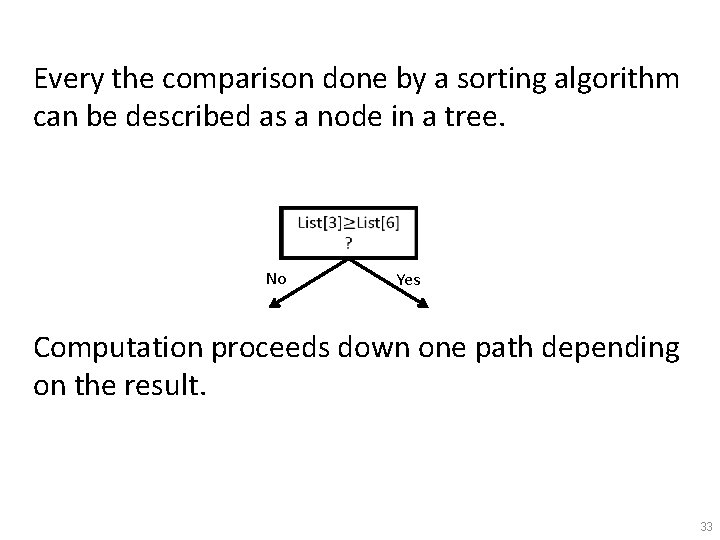
Every the comparison done by a sorting algorithm can be described as a node in a tree. No Yes Computation proceeds down one path depending on the result. 33

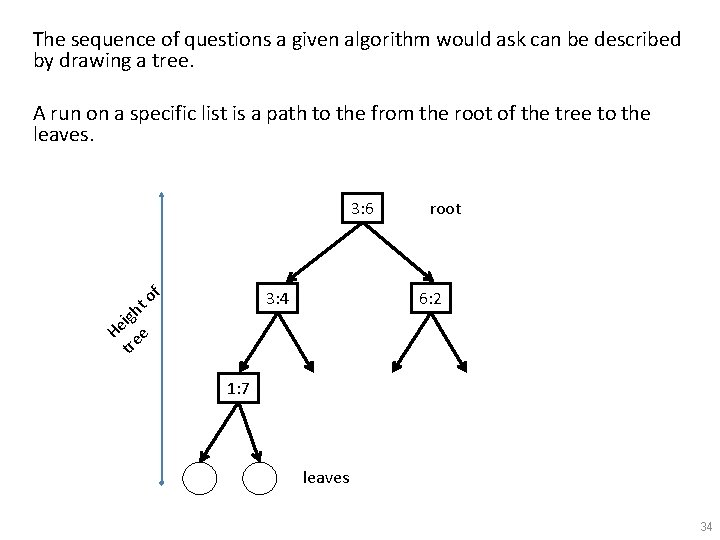
The sequence of questions a given algorithm would ask can be described by drawing a tree. A run on a specific list is a path to the from the root of the tree to the leaves. 3: 6 f t o igh e H ee tr 3: 4 root 6: 2 1: 7 leaves 34

Functions as parameters • Functions are also values in python! • Can be assigned, passed to functions, returned, etc. def my_fun(): print(“hi”) a = my_fun a() 37

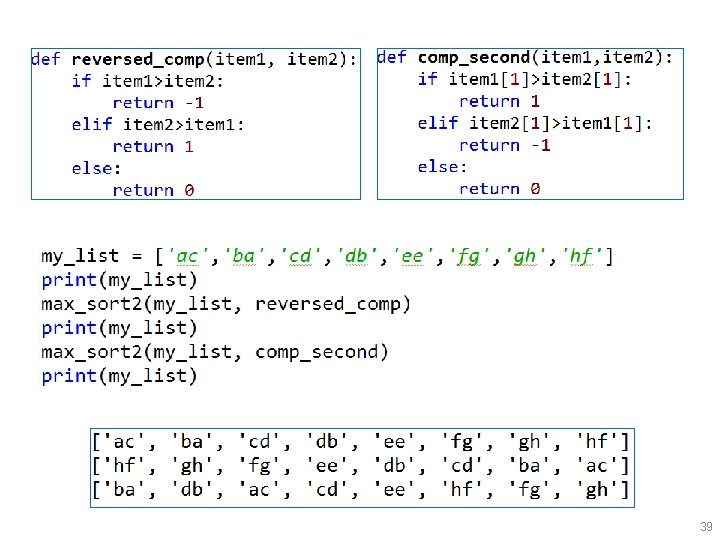
Example usage: A function that compares two arguments. Returns: positive number / 0 / negative number if first arg is greater / equal / smaller 38

39

Inside sorting code: 40

Extras 41

Finding Duplicate Values 42

Finding Duplicate Values • What is the running time? 43