Sorting Example Bubble Sort Problem Definition Sorting takes

Sorting Example Bubble Sort

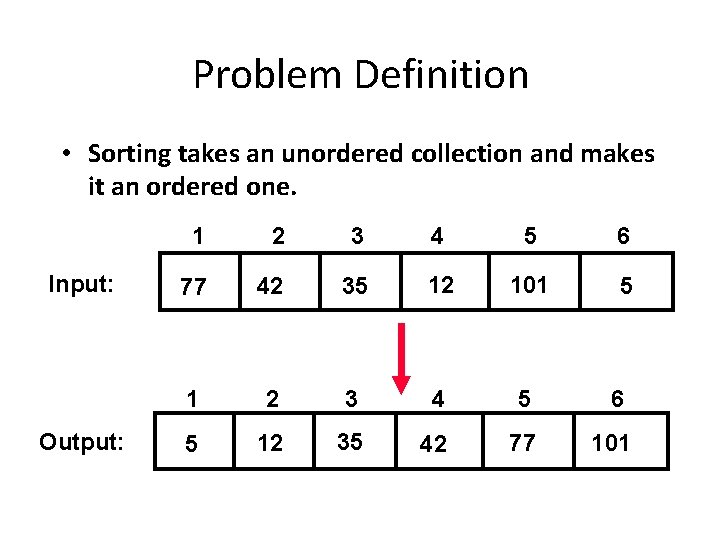
Problem Definition • Sorting takes an unordered collection and makes it an ordered one. Input: Output: 1 2 3 4 5 6 77 42 35 12 101 5 1 2 3 4 5 6 5 12 35 42 77 101

One Idea: Bubble Water 3 3 2 2 1 1 Air 3 3 2 2 1 1

"Bubbling Up" the Largest Element • Traverse a collection of elements – Move from the front to the end – “Bubble” the largest value to the end using pairwise comparisons and swapping 1 2 3 4 5 6 77 42 35 12 101 5

"Bubbling Up" the Largest Element • Traverse a collection of elements – Move from the front to the end – “Bubble” the largest value to the end using pairwise comparisons and swapping 1 2 3 4 5 6 42 Swap 77 42 77 35 12 101 5

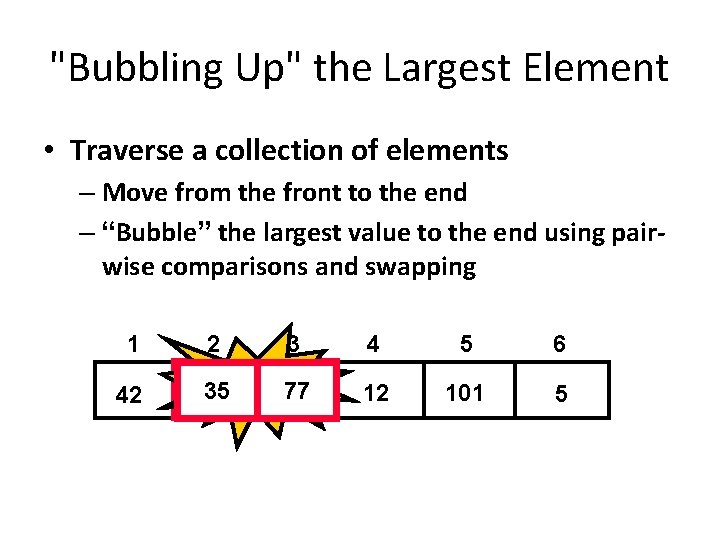
"Bubbling Up" the Largest Element • Traverse a collection of elements – Move from the front to the end – “Bubble” the largest value to the end using pairwise comparisons and swapping 1 42 2 3 35 Swap 35 77 77 4 5 6 12 101 5

"Bubbling Up" the Largest Element • Traverse a collection of elements – Move from the front to the end – “Bubble” the largest value to the end using pairwise comparisons and swapping 1 2 42 35 3 4 12 Swap 12 77 77 5 6 101 5

"Bubbling Up" the Largest Element • Traverse a collection of elements – Move from the front to the end – “Bubble” the largest value to the end using pairwise comparisons and swapping 1 2 3 4 5 6 42 35 12 77 101 5 No need to swap

"Bubbling Up" the Largest Element • Traverse a collection of elements – Move from the front to the end – “Bubble” the largest value to the end using pairwise comparisons and swapping 1 2 3 4 42 35 12 77 5 6 5 Swap 101 5

"Bubbling Up" the Largest Element • Traverse a collection of elements – Move from the front to the end – “Bubble” the largest value to the end using pairwise comparisons and swapping 1 2 3 4 5 6 42 35 12 77 5 101 Largest value correctly placed

The “Bubble Up” Algorithm Bubble-Sort-step 1( A ): for k = 1 … (N – 1): if A[k] > A[k+1]: Swap( A, k, k+1 ) Swap( A, x, y ): tmp = A[x] = A[y] = tmp Python Code in http: //www. geekviewpoint. com/python/sorting/bubblesort

Need More Iterations • Notice that only the largest value is correctly placed • All other values are still out of order • So we need to repeat this process 1 2 3 4 5 6 42 35 12 77 5 101 Largest value correctly placed

Repeat “Bubble Up” How Many Times? • If we have N elements… • And if each time we bubble an element, we place it in its correct location… • Then we repeat the “bubble up” process N – 1 times. • This guarantees we’ll correctly place all N elements.

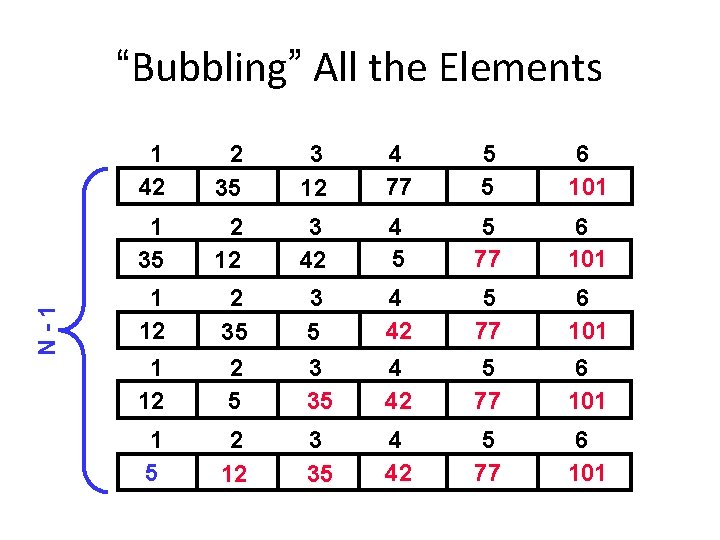
N-1 “Bubbling” All the Elements 1 42 2 35 3 12 4 77 5 5 6 101 1 35 2 12 3 42 4 5 5 77 6 101 1 12 3 5 3 35 4 42 5 77 6 101 1 12 2 35 2 5 4 42 5 77 6 101 1 5 2 12 3 35 4 42 5 77 6 101

The “Bubble Up” Algorithm Bubble-Sort( A ): for k = 1 … (N – 1): if A[k] > A[k+1]: Swap( A, k, k+1 ) Python Code in http: //www. geekviewpoint. com/python/sorting/bubblesort

The “Bubble Up” Algorithm Bubble-Sort( A ): for i = 1 … (N – 1): for k = 1 … (N – 1): if A[k] > A[k+1]: Swap( A, k, k+1 ) Python Code in http: //www. geekviewpoint. com/python/sorting/bubblesort

The “Bubble Up” Algorithm Bubble-Sort( A ): To do N-1 iterations for i = 1 … (N – 1): Python Code in http: //www. geekviewpoint. com/python/sorting/bubblesort Outer loop for k = 1 … (N – 1): if A[k] > A[k+1]: Swap( A, k, k+1 ) Inner loop To bubble a value

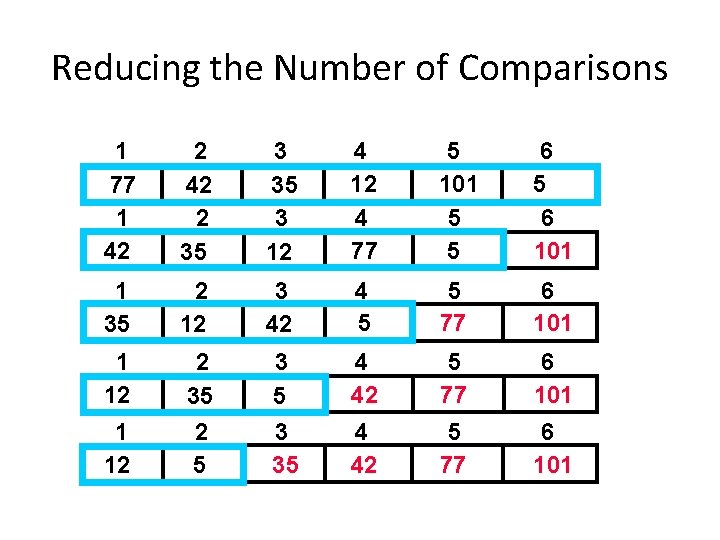
Reducing the Number of Comparisons 1 77 1 42 2 35 3 12 4 77 5 101 5 5 6 101 1 35 2 12 3 42 4 5 5 77 6 101 1 12 2 35 3 5 4 42 5 77 6 101 1 12 2 5 3 35 4 42 5 77 6 101

Reducing the Number of Comparisons • Assume the array size N • On the ith iteration, we only need to do N-i comparisons. • For example: – N=6 – i = 4 (4 th iteration) – Thus, we have 2 comparisons to do 1 12 2 35 3 5 4 42 5 77 6 101

The “Bubble Up” Algorithm Bubble-Sort( A ): for i = 1 … (N – 1): for k = 1 … (N – 1): if A[k] > A[k+1]: Swap( A, k, k+1 ) Python Code in http: //www. geekviewpoint. com/python/sorting/bubblesort

The “Bubble Up” Algorithm Bubble-Sort( A ): for i = 1 … (N – 1): for k = 1 … (N – i): if A[k] > A[k+1]: Swap( A, k, k+1 ) Python Code in http: //www. geekviewpoint. com/python/sorting/bubblesort

Code Demo

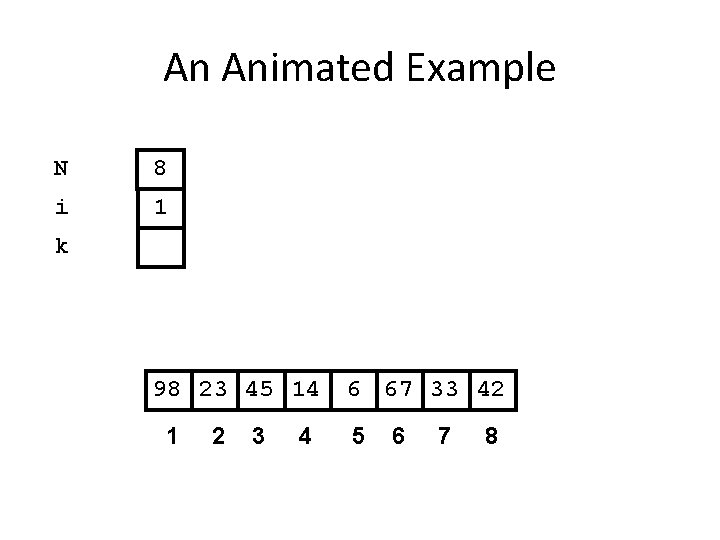
An Animated Example N 8 i 1 k 98 23 45 14 1 2 3 4 6 67 33 42 5 6 7 8

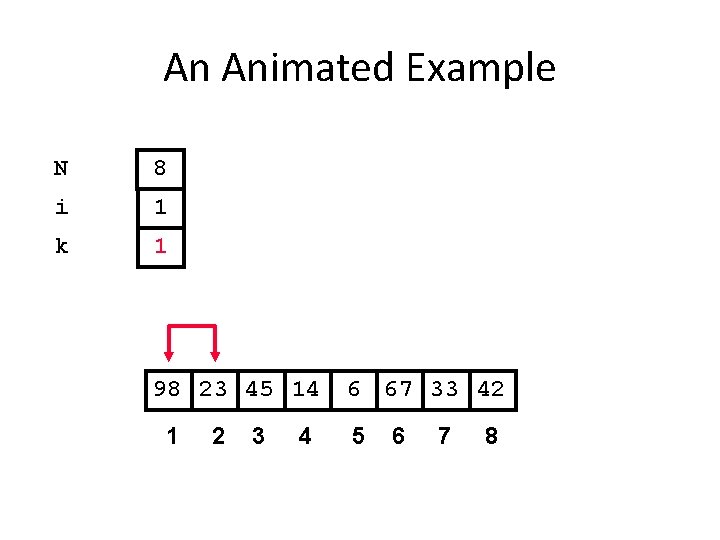
An Animated Example N 8 i 1 k 1 98 23 45 14 1 2 3 4 6 67 33 42 5 6 7 8

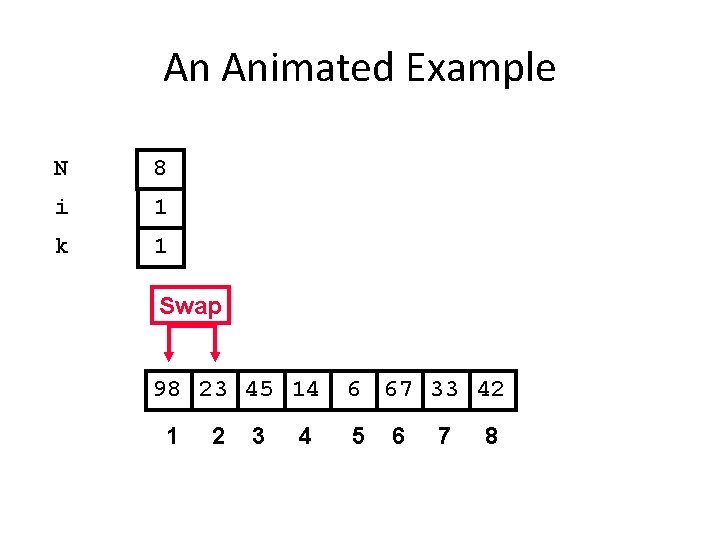
An Animated Example N 8 i 1 k 1 Swap 98 23 45 14 1 2 3 4 6 67 33 42 5 6 7 8

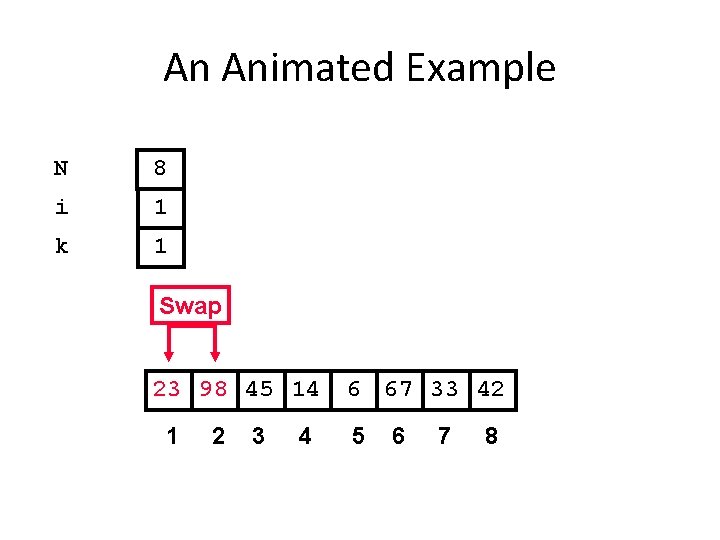
An Animated Example N 8 i 1 k 1 Swap 23 98 45 14 1 2 3 4 6 67 33 42 5 6 7 8

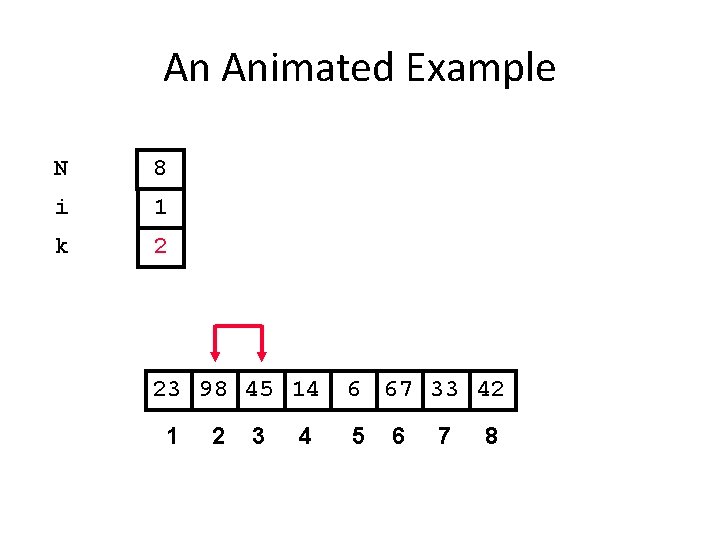
An Animated Example N 8 i 1 k 2 23 98 45 14 1 2 3 4 6 67 33 42 5 6 7 8

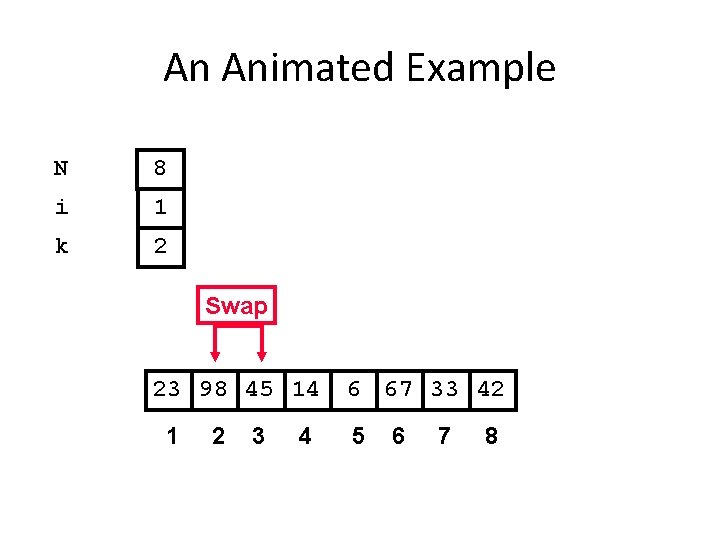
An Animated Example N 8 i 1 k 2 Swap 23 98 45 14 1 2 3 4 6 67 33 42 5 6 7 8

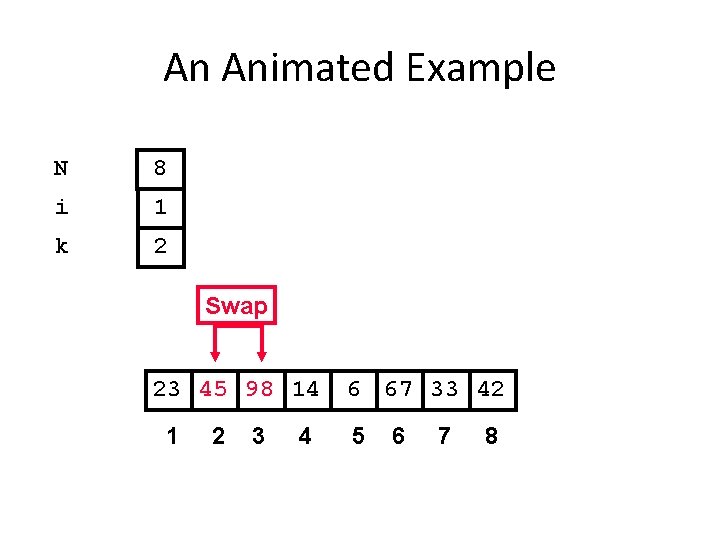
An Animated Example N 8 i 1 k 2 Swap 23 45 98 14 1 2 3 4 6 67 33 42 5 6 7 8

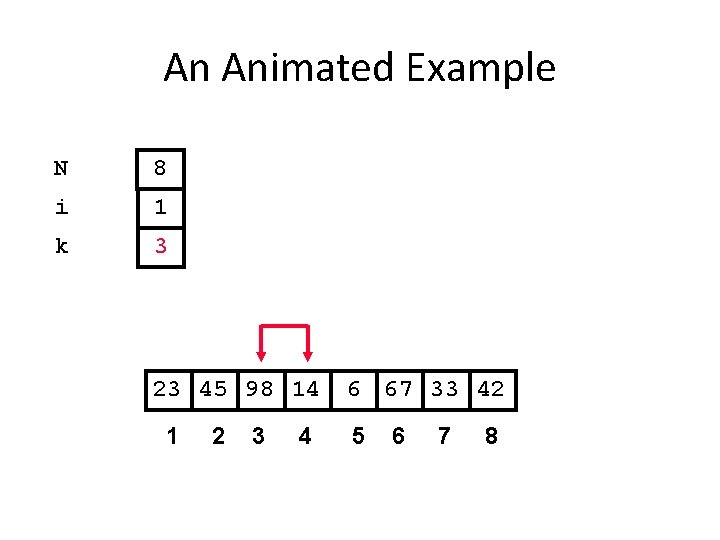
An Animated Example N 8 i 1 k 3 23 45 98 14 1 2 3 4 6 67 33 42 5 6 7 8

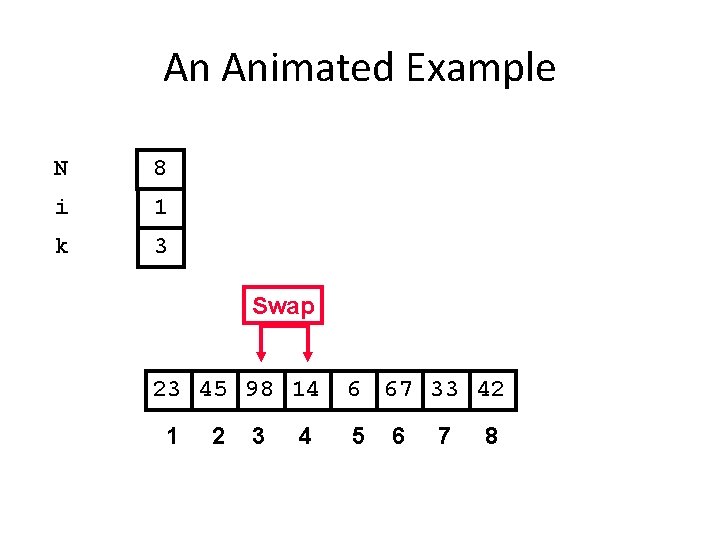
An Animated Example N 8 i 1 k 3 Swap 23 45 98 14 1 2 3 4 6 67 33 42 5 6 7 8

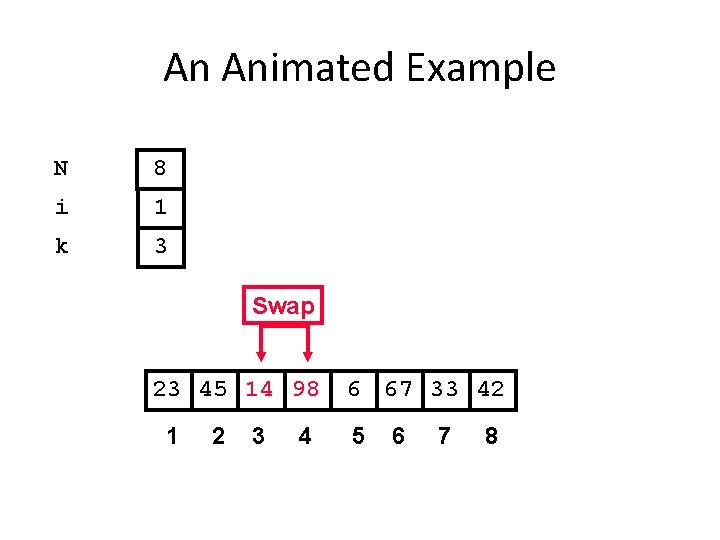
An Animated Example N 8 i 1 k 3 Swap 23 45 14 98 1 2 3 4 6 67 33 42 5 6 7 8

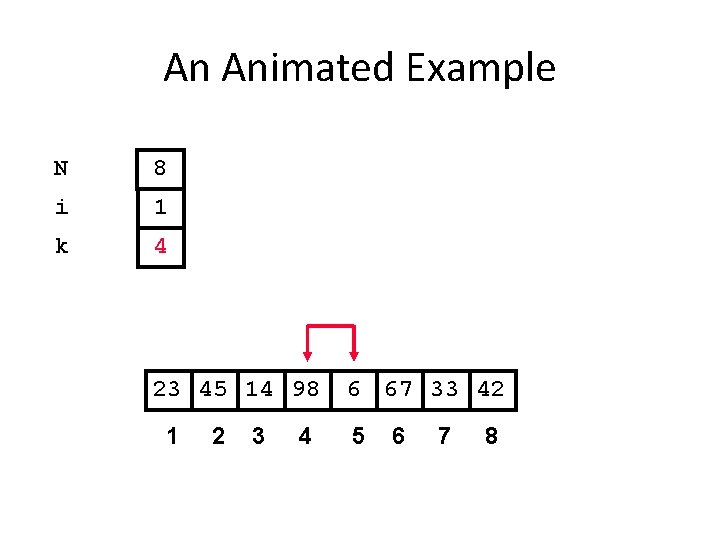
An Animated Example N 8 i 1 k 4 23 45 14 98 1 2 3 4 6 67 33 42 5 6 7 8

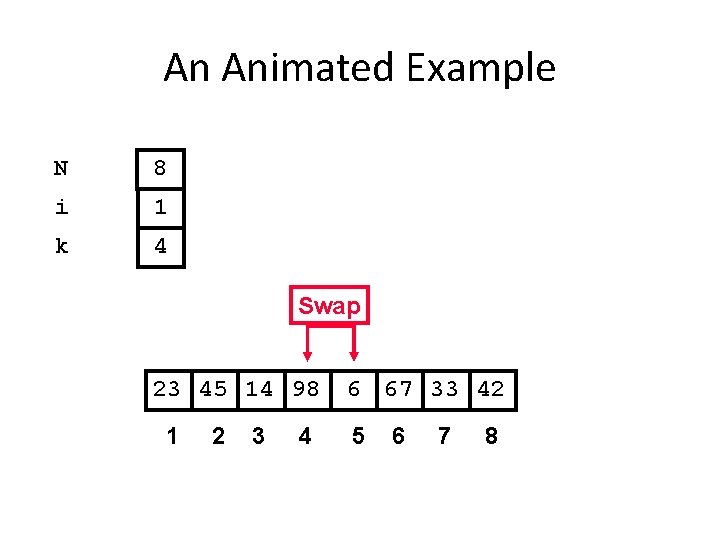
An Animated Example N 8 i 1 k 4 Swap 23 45 14 98 1 2 3 4 6 67 33 42 5 6 7 8

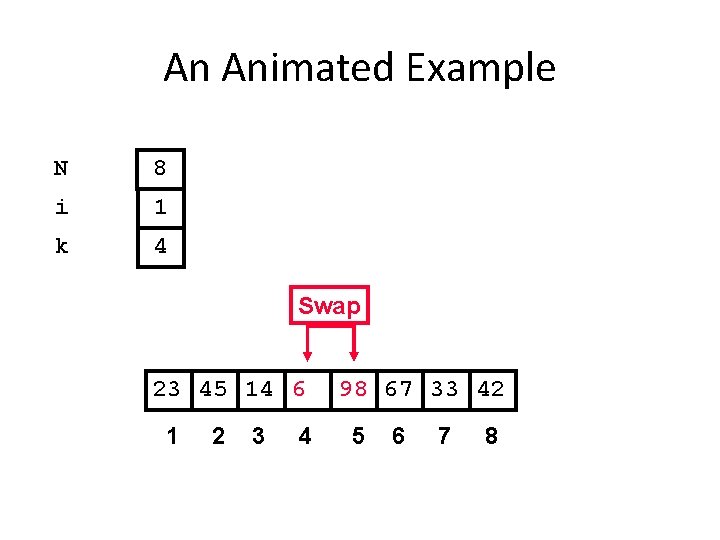
An Animated Example N 8 i 1 k 4 Swap 23 45 14 6 1 2 3 4 98 67 33 42 5 6 7 8

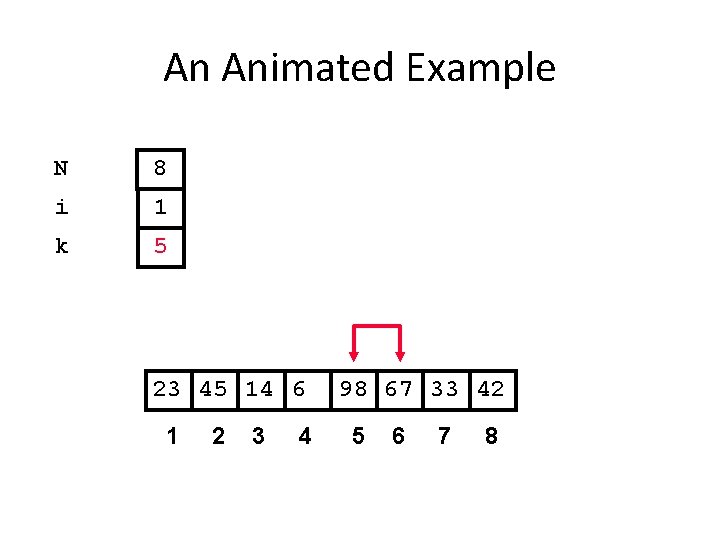
An Animated Example N 8 i 1 k 5 23 45 14 6 1 2 3 4 98 67 33 42 5 6 7 8

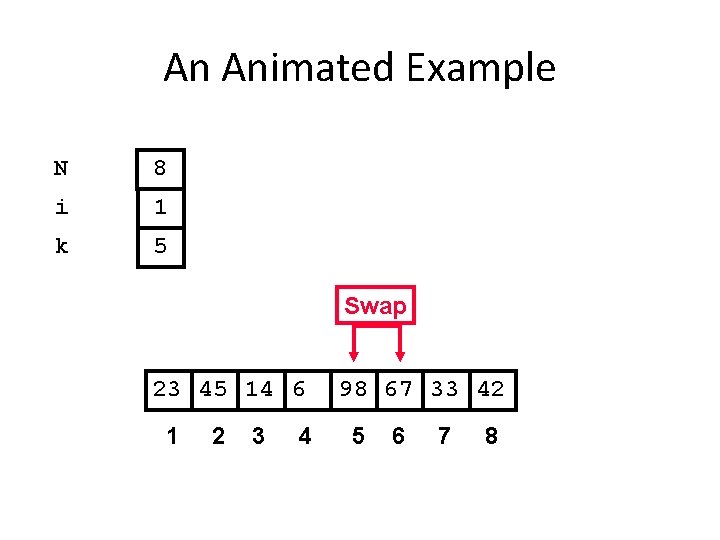
An Animated Example N 8 i 1 k 5 Swap 23 45 14 6 1 2 3 4 98 67 33 42 5 6 7 8

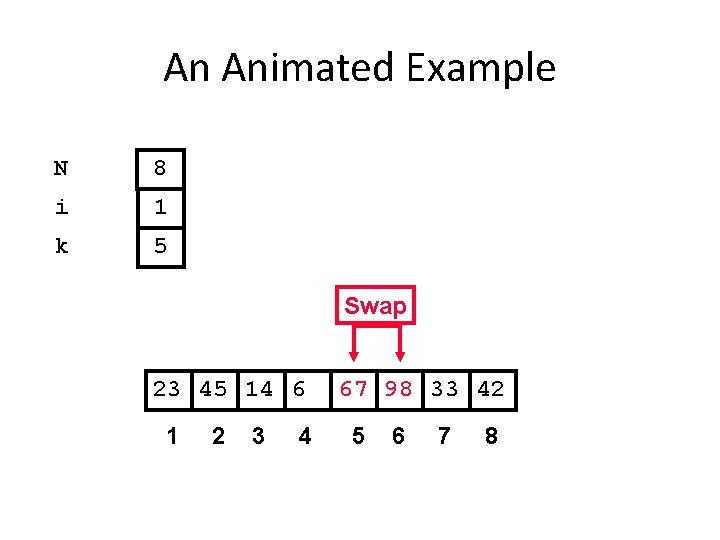
An Animated Example N 8 i 1 k 5 Swap 23 45 14 6 1 2 3 4 67 98 33 42 5 6 7 8

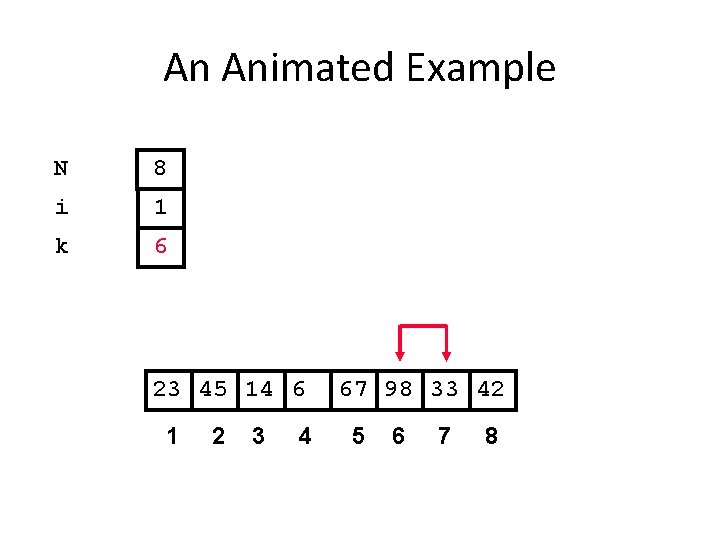
An Animated Example N 8 i 1 k 6 23 45 14 6 1 2 3 4 67 98 33 42 5 6 7 8

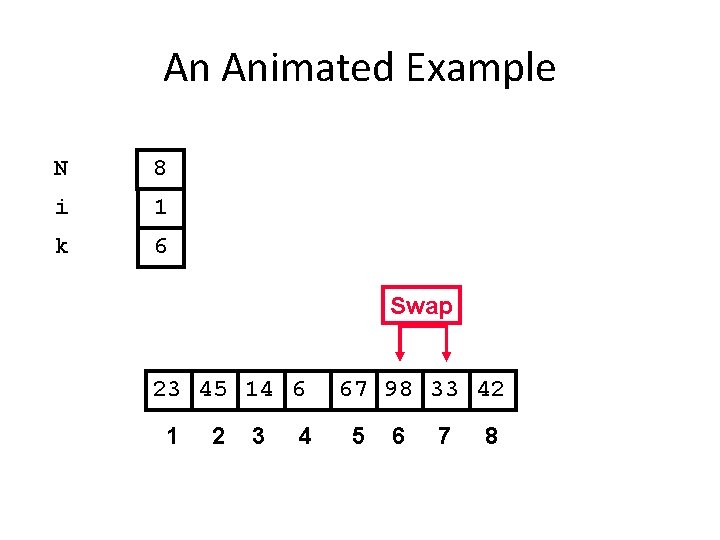
An Animated Example N 8 i 1 k 6 Swap 23 45 14 6 1 2 3 4 67 98 33 42 5 6 7 8

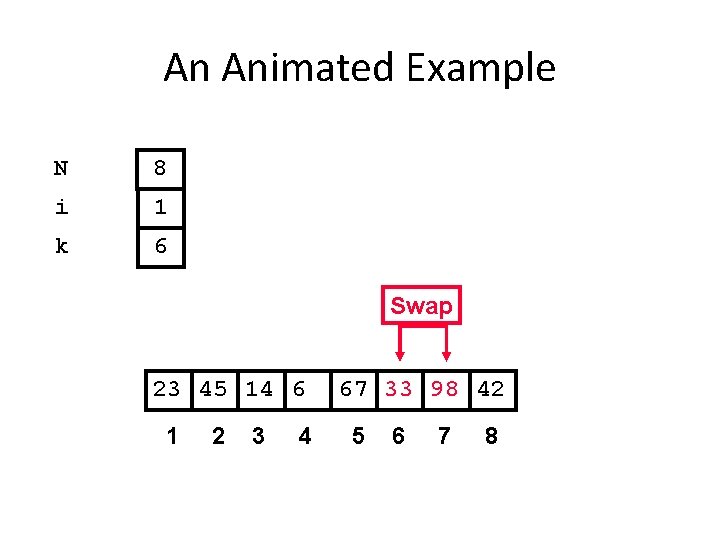
An Animated Example N 8 i 1 k 6 Swap 23 45 14 6 1 2 3 4 67 33 98 42 5 6 7 8

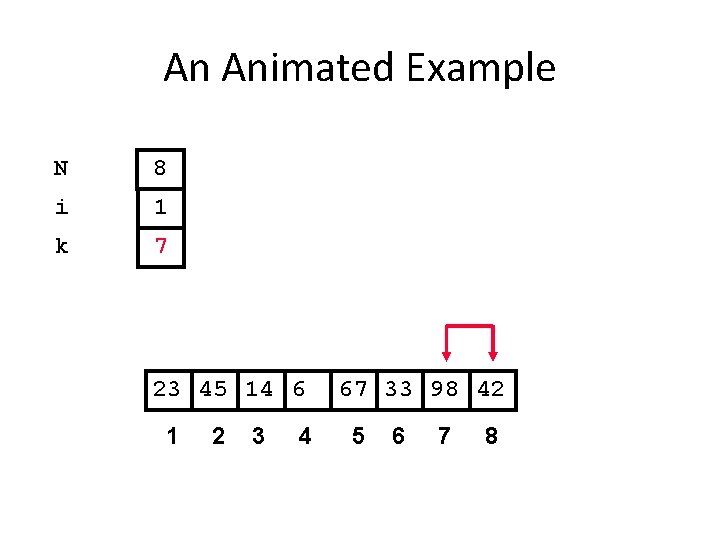
An Animated Example N 8 i 1 k 7 23 45 14 6 1 2 3 4 67 33 98 42 5 6 7 8

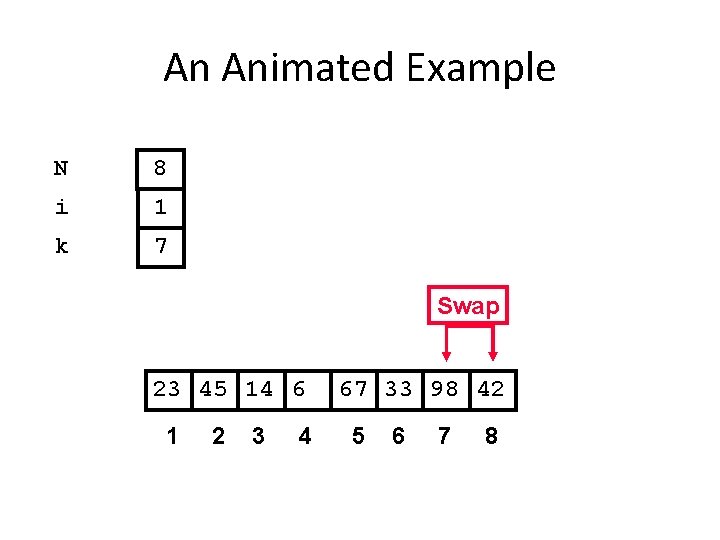
An Animated Example N 8 i 1 k 7 Swap 23 45 14 6 1 2 3 4 67 33 98 42 5 6 7 8

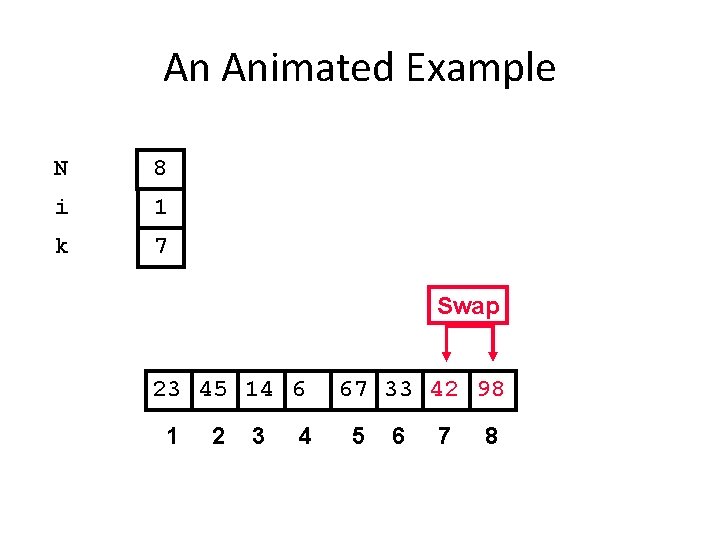
An Animated Example N 8 i 1 k 7 Swap 23 45 14 6 1 2 3 4 67 33 42 98 5 6 7 8

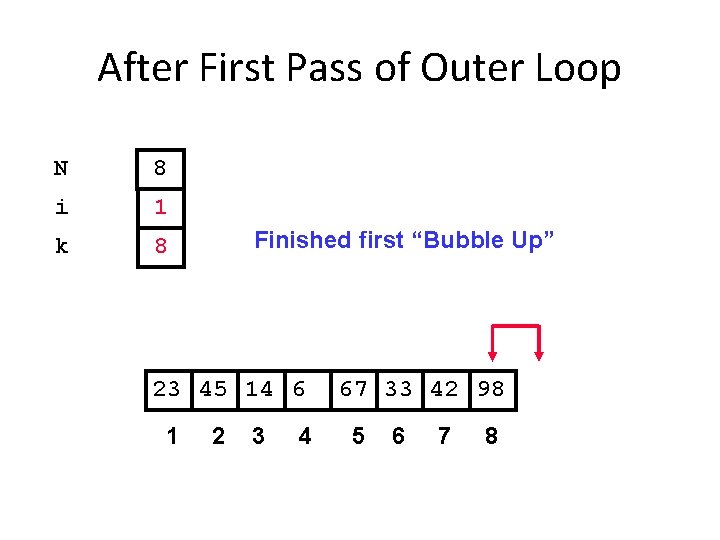
After First Pass of Outer Loop N 8 i 1 k 8 Finished first “Bubble Up” 23 45 14 6 1 2 3 4 67 33 42 98 5 6 7 8

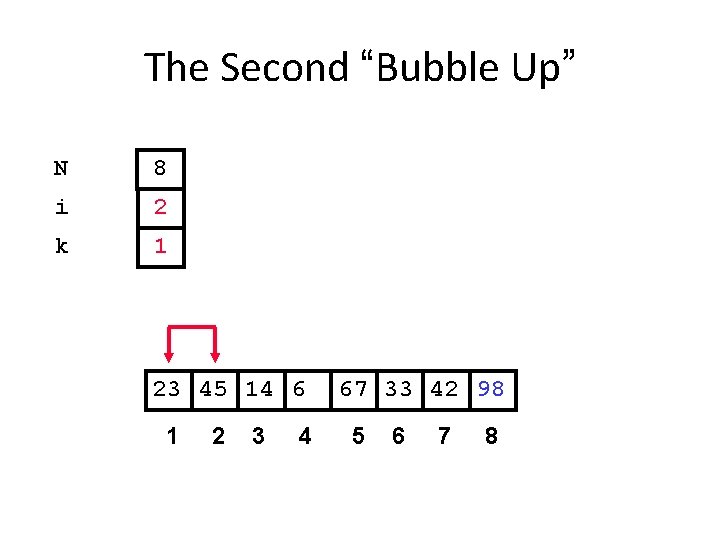
The Second “Bubble Up” N 8 i 2 k 1 23 45 14 6 1 2 3 4 67 33 42 98 5 6 7 8

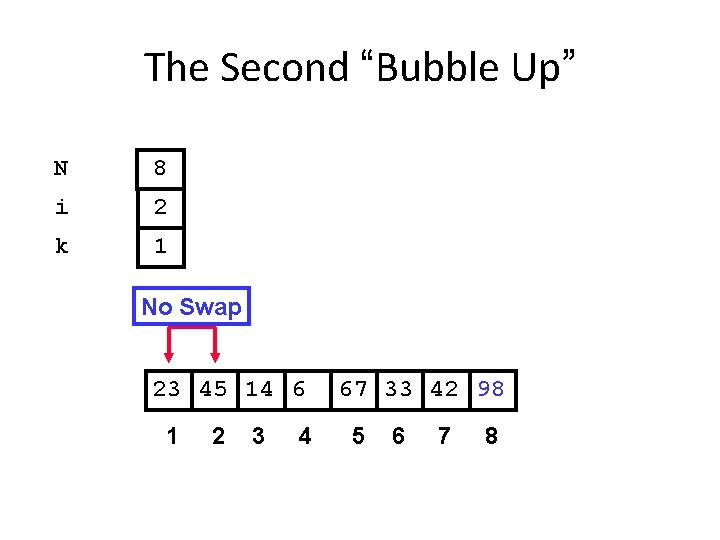
The Second “Bubble Up” N 8 i 2 k 1 No Swap 23 45 14 6 1 2 3 4 67 33 42 98 5 6 7 8

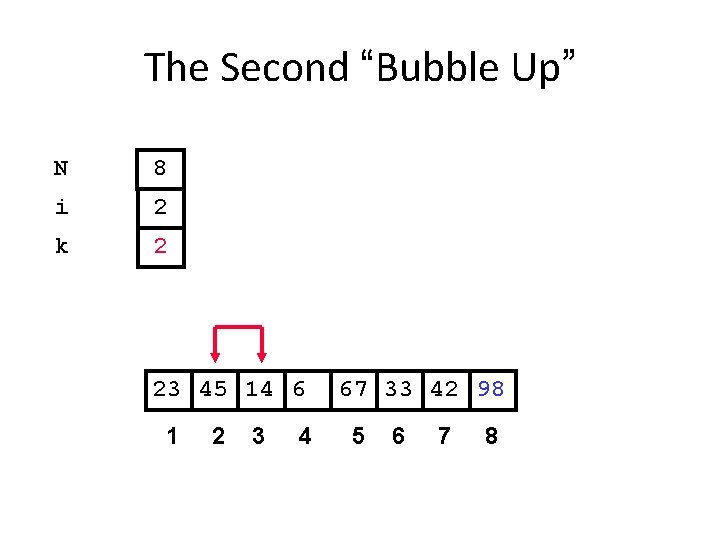
The Second “Bubble Up” N 8 i 2 k 2 23 45 14 6 1 2 3 4 67 33 42 98 5 6 7 8

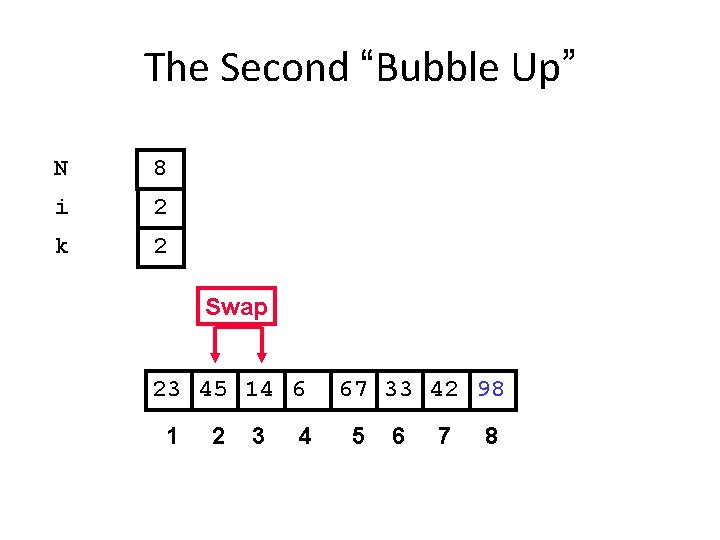
The Second “Bubble Up” N 8 i 2 k 2 Swap 23 45 14 6 1 2 3 4 67 33 42 98 5 6 7 8

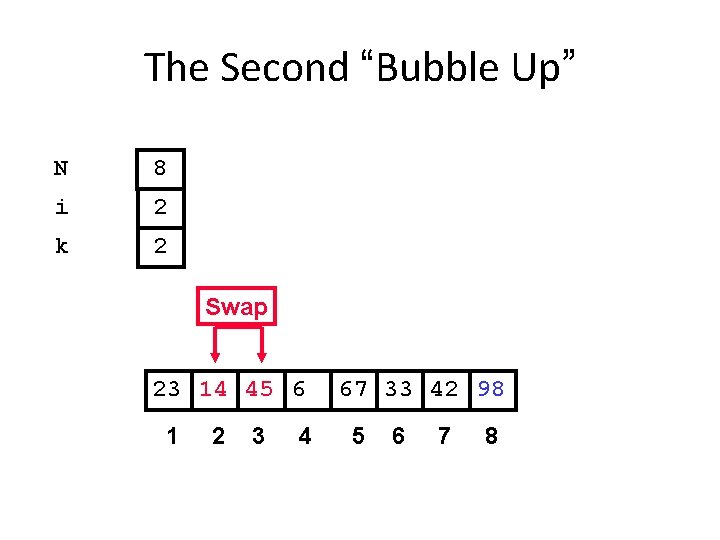
The Second “Bubble Up” N 8 i 2 k 2 Swap 23 14 45 6 1 2 3 4 67 33 42 98 5 6 7 8

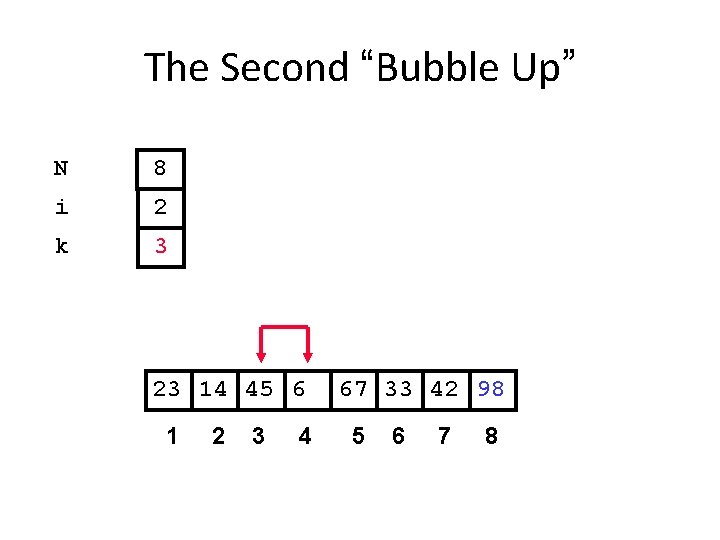
The Second “Bubble Up” N 8 i 2 k 3 23 14 45 6 1 2 3 4 67 33 42 98 5 6 7 8

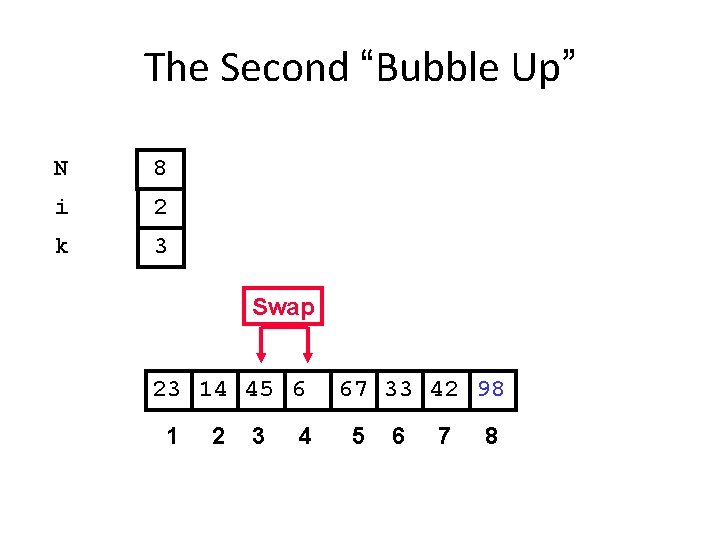
The Second “Bubble Up” N 8 i 2 k 3 Swap 23 14 45 6 1 2 3 4 67 33 42 98 5 6 7 8

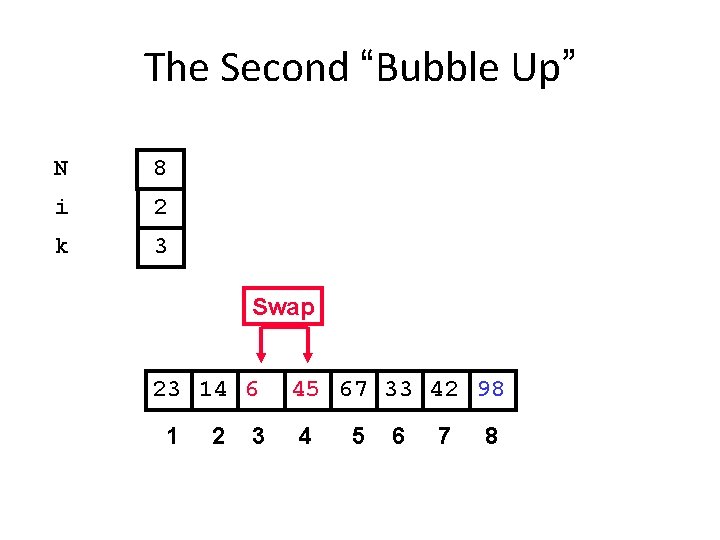
The Second “Bubble Up” N 8 i 2 k 3 Swap 23 14 6 1 2 3 45 67 33 42 98 4 5 6 7 8

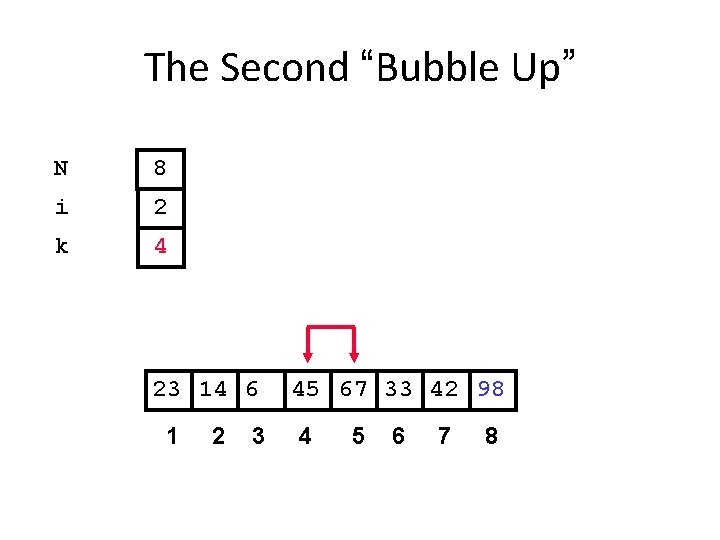
The Second “Bubble Up” N 8 i 2 k 4 23 14 6 1 2 3 45 67 33 42 98 4 5 6 7 8

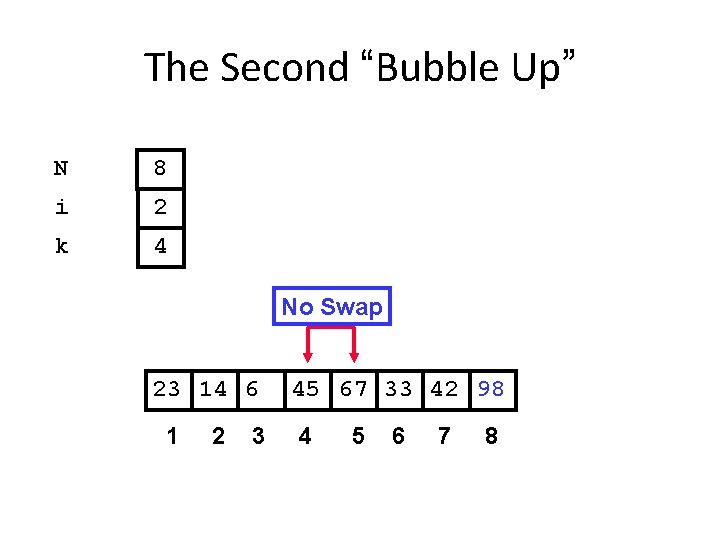
The Second “Bubble Up” N 8 i 2 k 4 No Swap 23 14 6 1 2 3 45 67 33 42 98 4 5 6 7 8

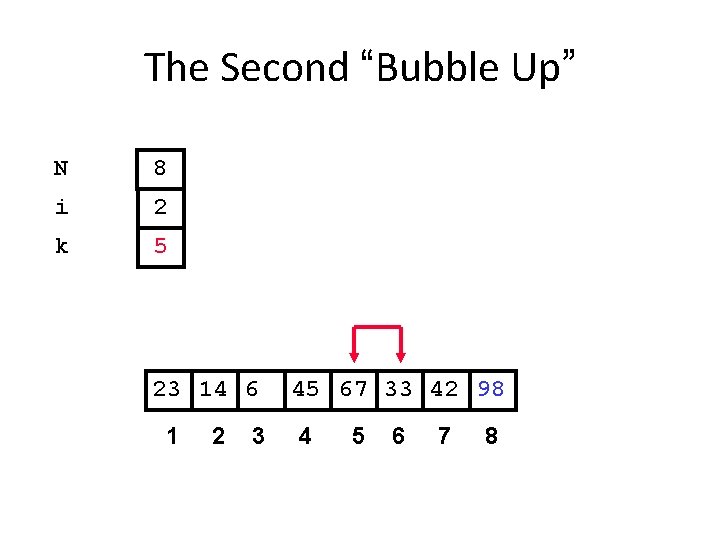
The Second “Bubble Up” N 8 i 2 k 5 23 14 6 1 2 3 45 67 33 42 98 4 5 6 7 8

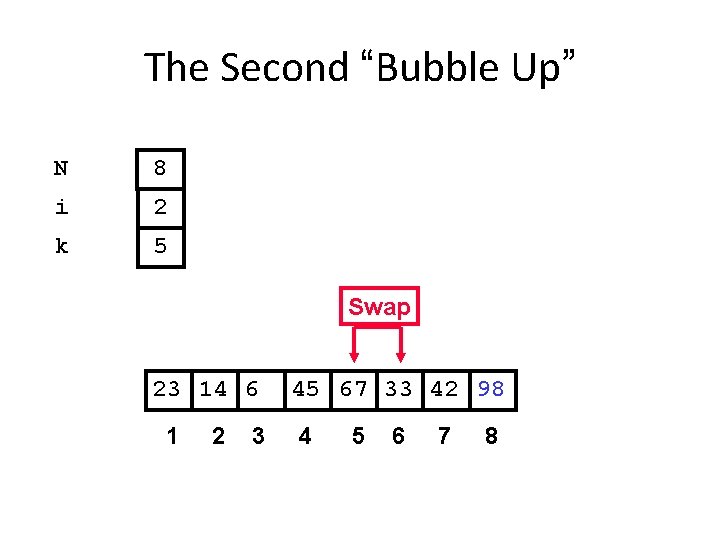
The Second “Bubble Up” N 8 i 2 k 5 Swap 23 14 6 1 2 3 45 67 33 42 98 4 5 6 7 8

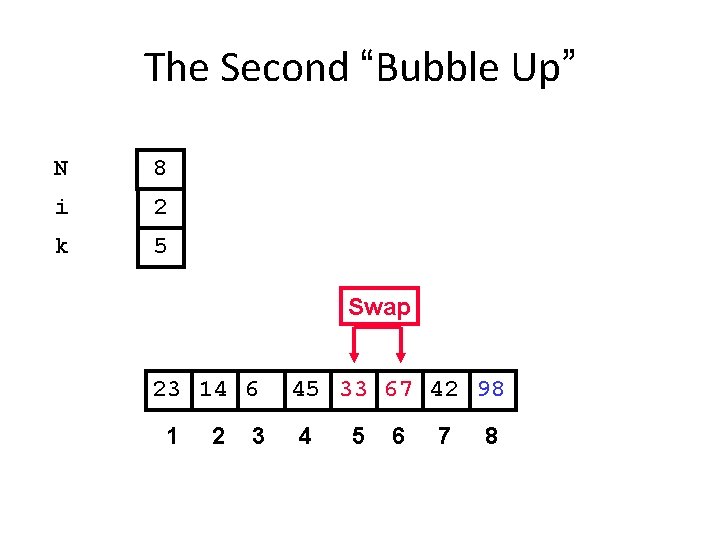
The Second “Bubble Up” N 8 i 2 k 5 Swap 23 14 6 1 2 3 45 33 67 42 98 4 5 6 7 8

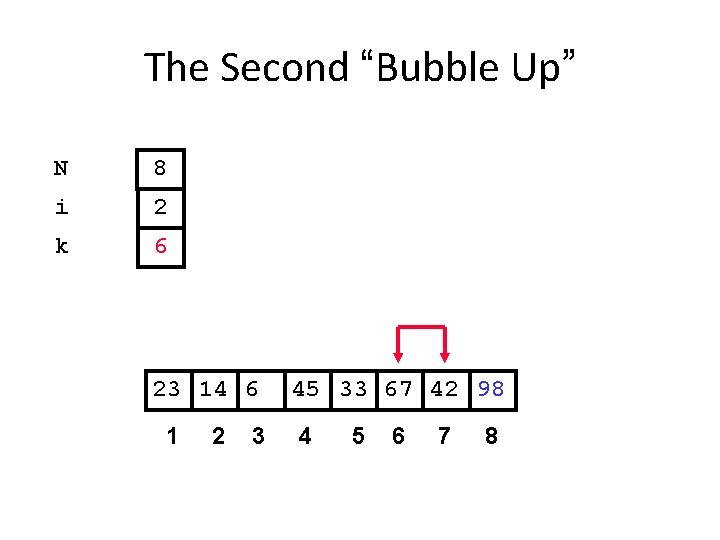
The Second “Bubble Up” N 8 i 2 k 6 23 14 6 1 2 3 45 33 67 42 98 4 5 6 7 8

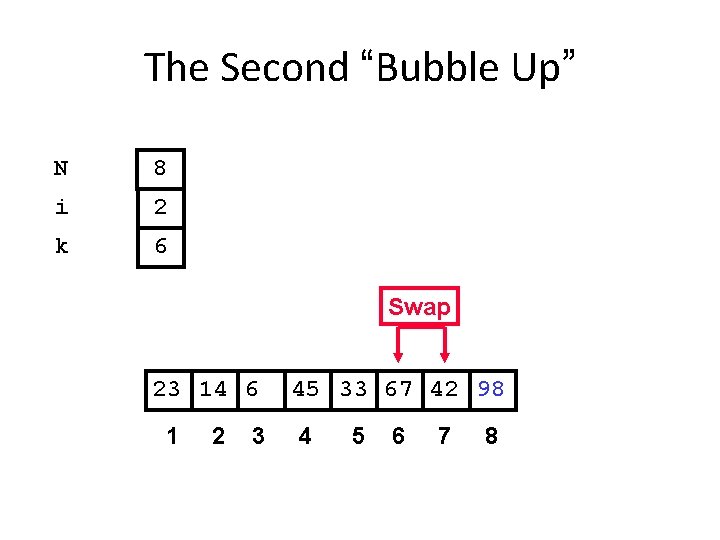
The Second “Bubble Up” N 8 i 2 k 6 Swap 23 14 6 1 2 3 45 33 67 42 98 4 5 6 7 8

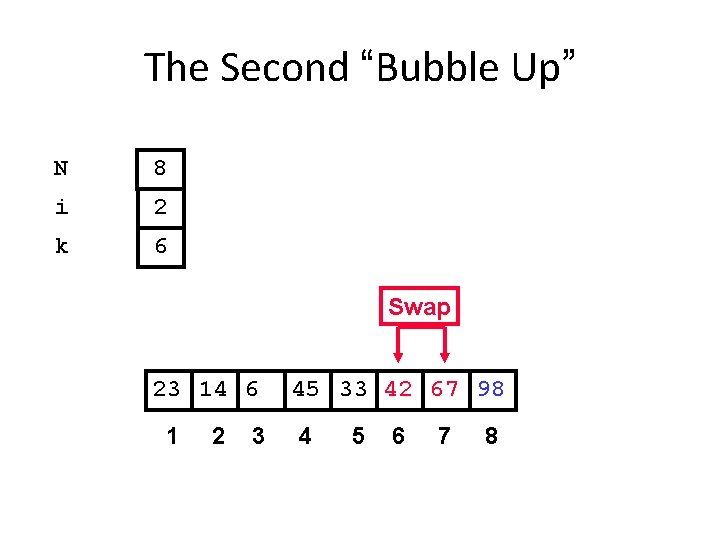
The Second “Bubble Up” N 8 i 2 k 6 Swap 23 14 6 1 2 3 45 33 42 67 98 4 5 6 7 8

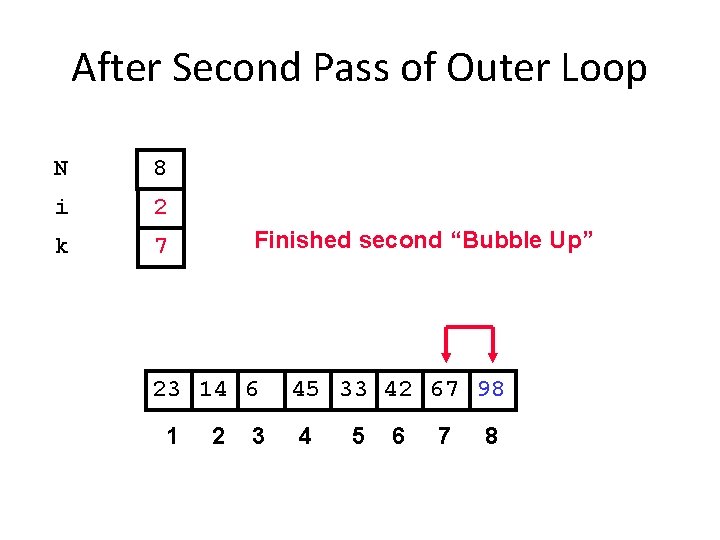
After Second Pass of Outer Loop N 8 i 2 k 7 Finished second “Bubble Up” 23 14 6 1 2 3 45 33 42 67 98 4 5 6 7 8

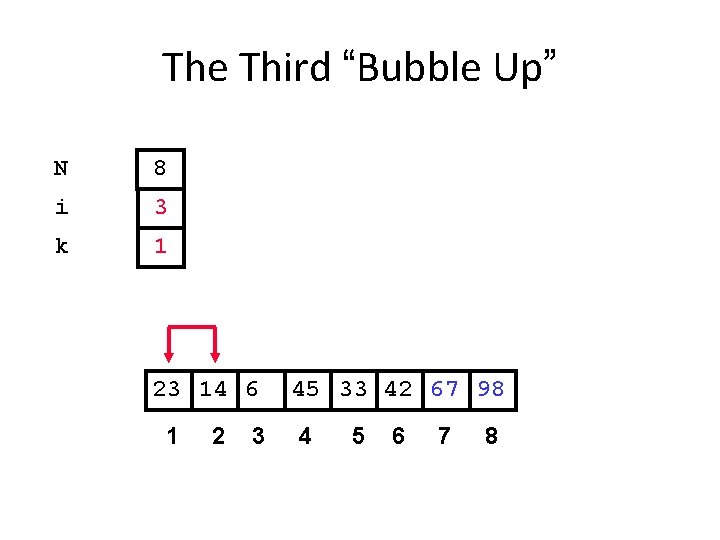
The Third “Bubble Up” N 8 i 3 k 1 23 14 6 1 2 3 45 33 42 67 98 4 5 6 7 8

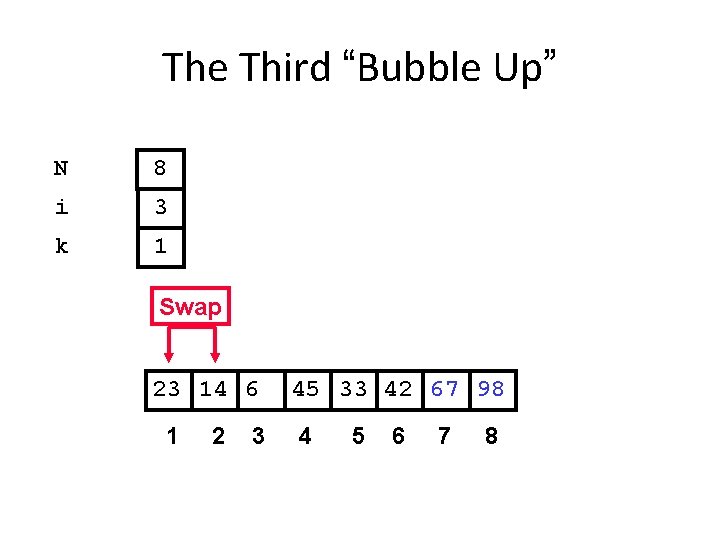
The Third “Bubble Up” N 8 i 3 k 1 Swap 23 14 6 1 2 3 45 33 42 67 98 4 5 6 7 8

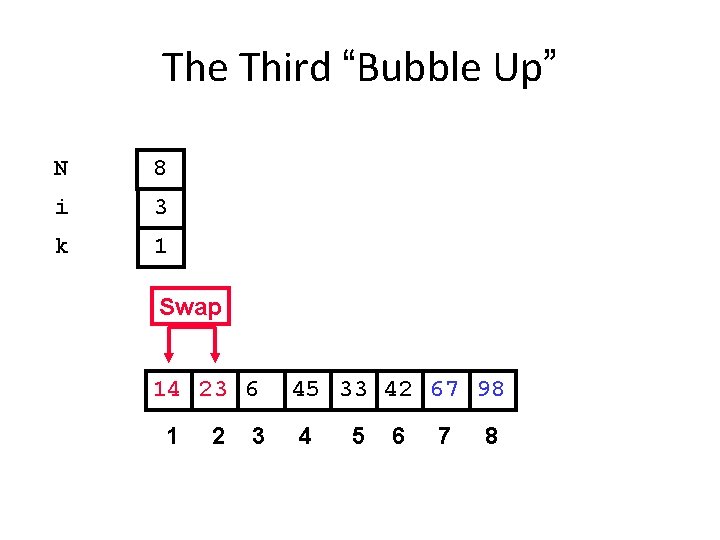
The Third “Bubble Up” N 8 i 3 k 1 Swap 14 23 6 1 2 3 45 33 42 67 98 4 5 6 7 8

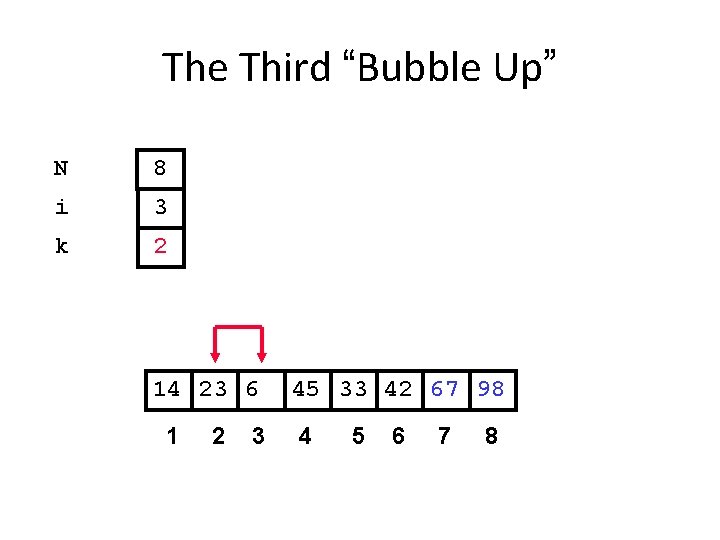
The Third “Bubble Up” N 8 i 3 k 2 14 23 6 1 2 3 45 33 42 67 98 4 5 6 7 8

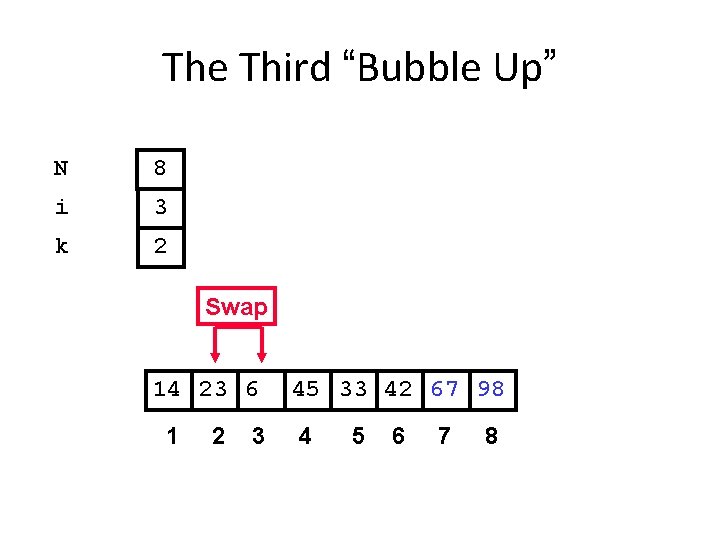
The Third “Bubble Up” N 8 i 3 k 2 Swap 14 23 6 1 2 3 45 33 42 67 98 4 5 6 7 8

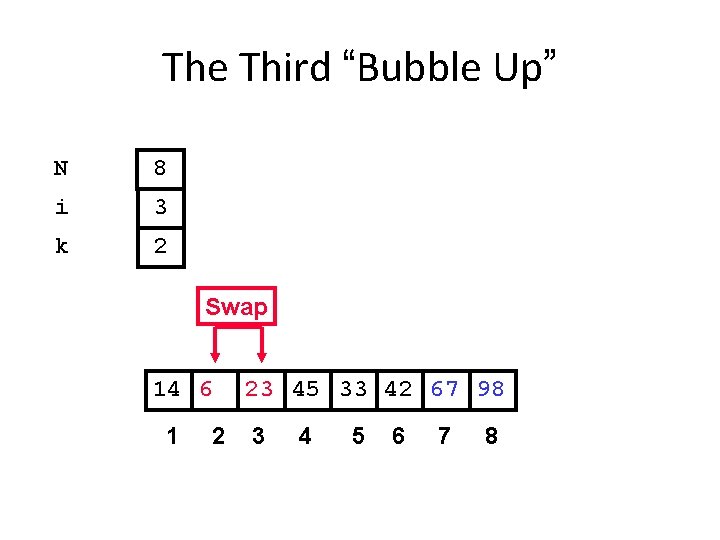
The Third “Bubble Up” N 8 i 3 k 2 Swap 14 6 1 2 23 45 33 42 67 98 3 4 5 6 7 8

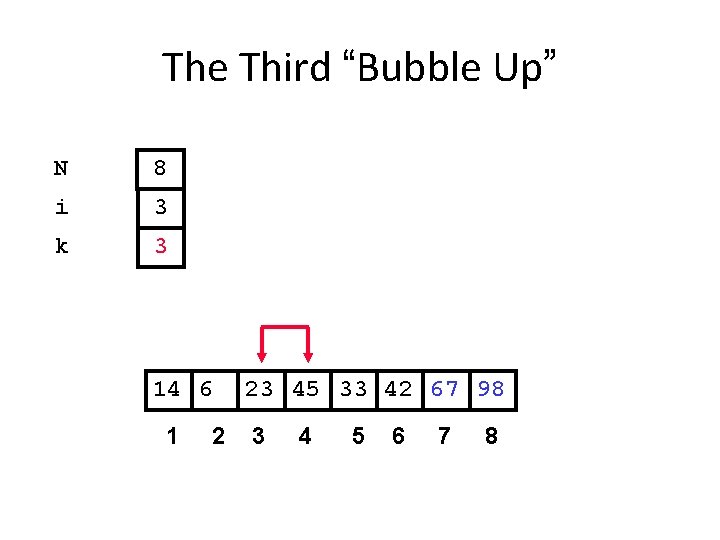
The Third “Bubble Up” N 8 i 3 k 3 14 6 1 2 23 45 33 42 67 98 3 4 5 6 7 8

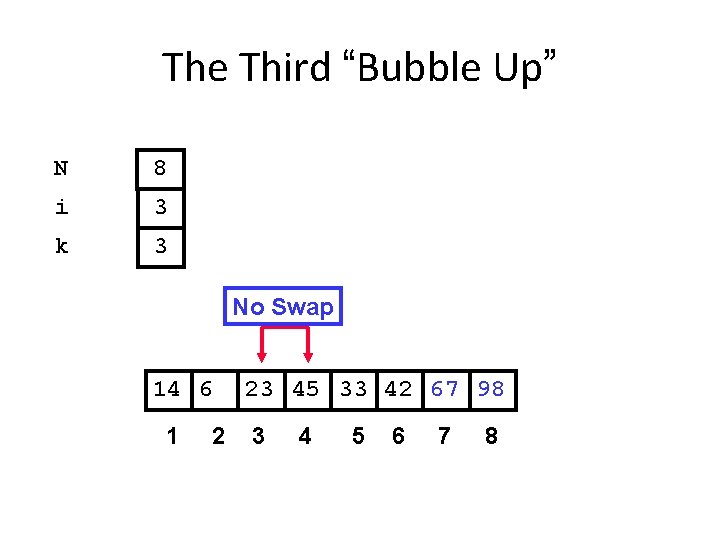
The Third “Bubble Up” N 8 i 3 k 3 No Swap 14 6 1 2 23 45 33 42 67 98 3 4 5 6 7 8

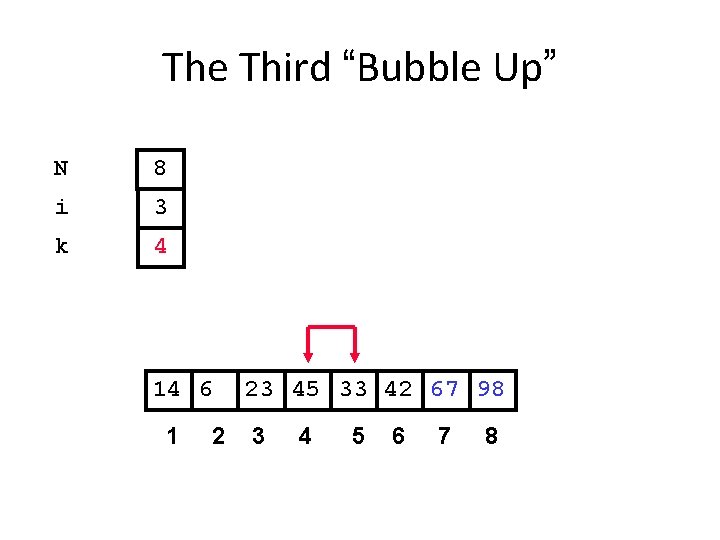
The Third “Bubble Up” N 8 i 3 k 4 14 6 1 2 23 45 33 42 67 98 3 4 5 6 7 8

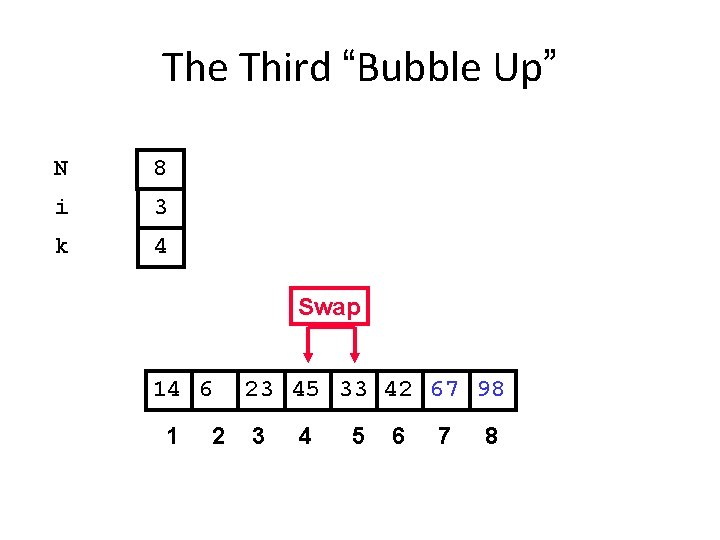
The Third “Bubble Up” N 8 i 3 k 4 Swap 14 6 1 2 23 45 33 42 67 98 3 4 5 6 7 8

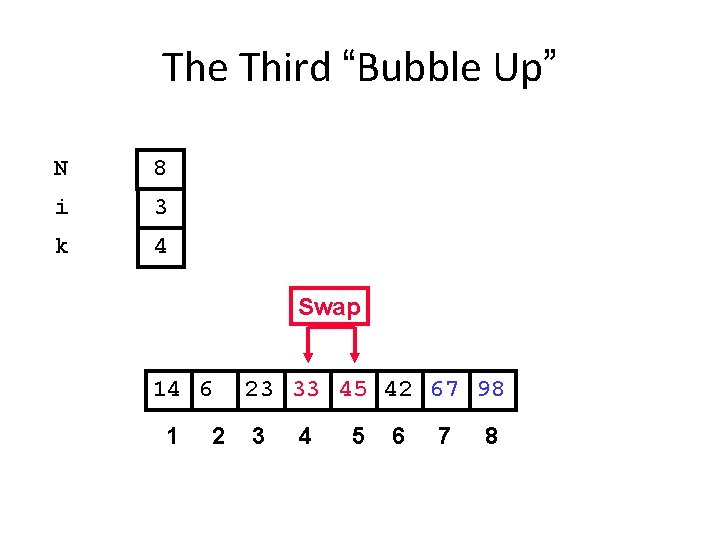
The Third “Bubble Up” N 8 i 3 k 4 Swap 14 6 1 2 23 33 45 42 67 98 3 4 5 6 7 8

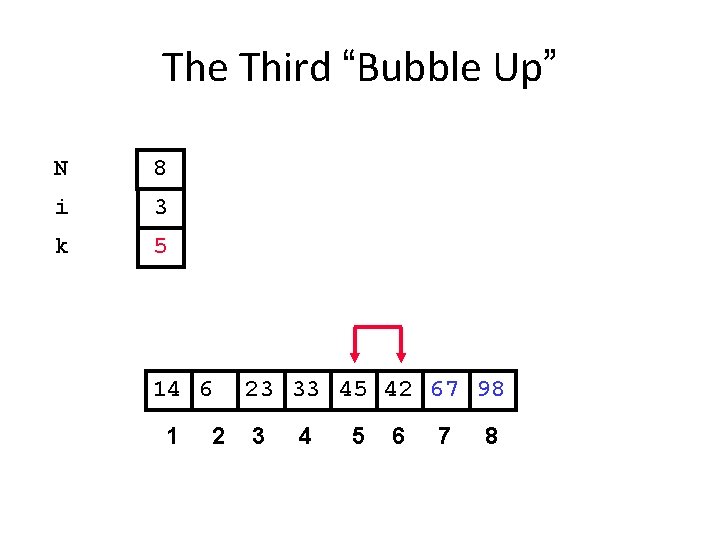
The Third “Bubble Up” N 8 i 3 k 5 14 6 1 2 23 33 45 42 67 98 3 4 5 6 7 8

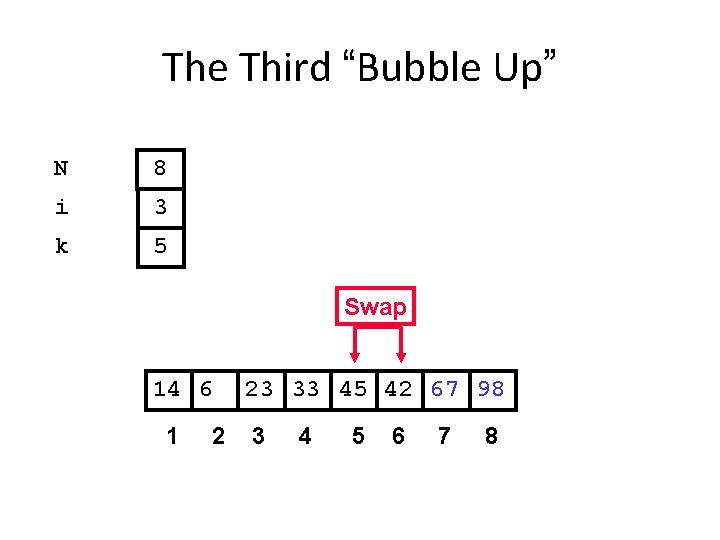
The Third “Bubble Up” N 8 i 3 k 5 Swap 14 6 1 2 23 33 45 42 67 98 3 4 5 6 7 8

The Third “Bubble Up” N 8 i 3 k 5 Swap 14 6 1 2 23 33 42 45 67 98 3 4 5 6 7 8

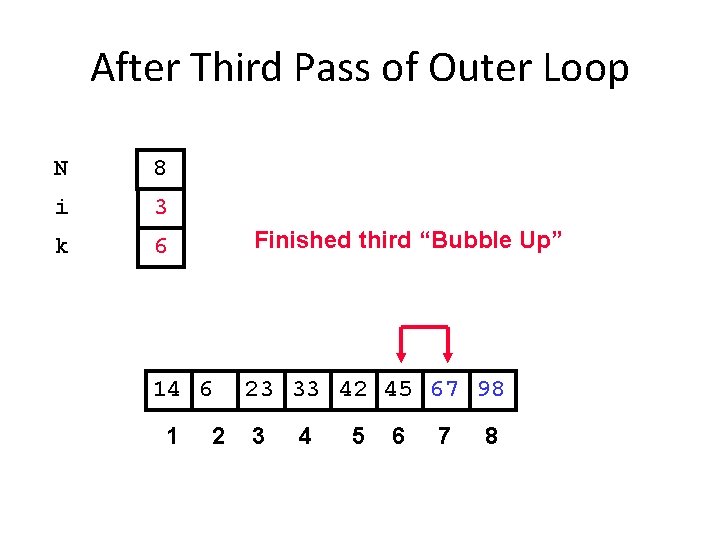
After Third Pass of Outer Loop N 8 i 3 k 6 Finished third “Bubble Up” 14 6 1 2 23 33 42 45 67 98 3 4 5 6 7 8

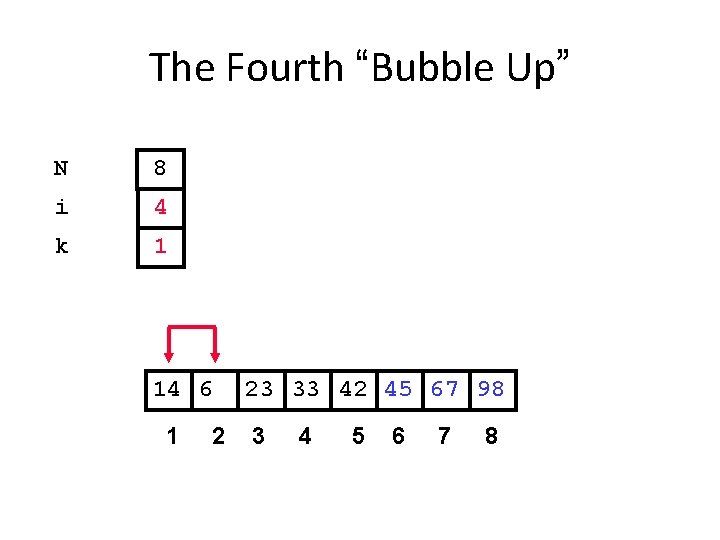
The Fourth “Bubble Up” N 8 i 4 k 1 14 6 1 2 23 33 42 45 67 98 3 4 5 6 7 8

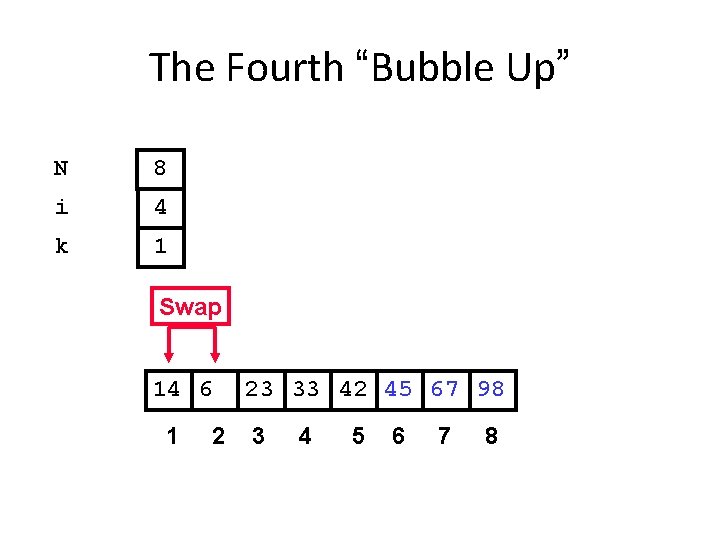
The Fourth “Bubble Up” N 8 i 4 k 1 Swap 14 6 1 2 23 33 42 45 67 98 3 4 5 6 7 8

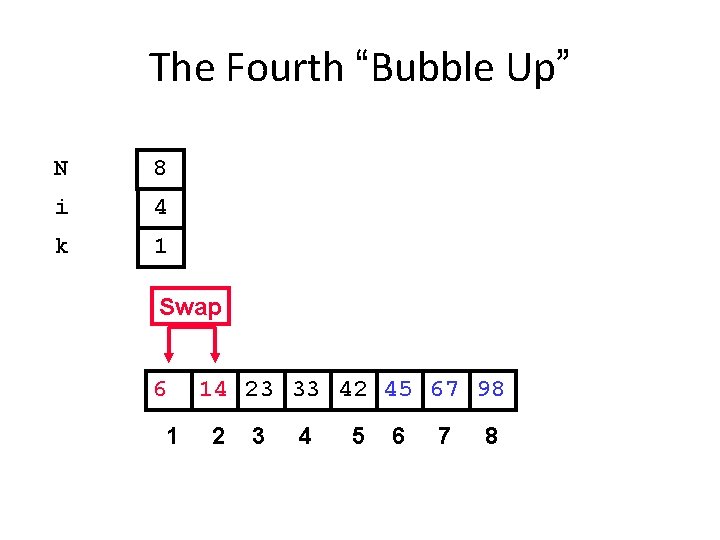
The Fourth “Bubble Up” N 8 i 4 k 1 Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

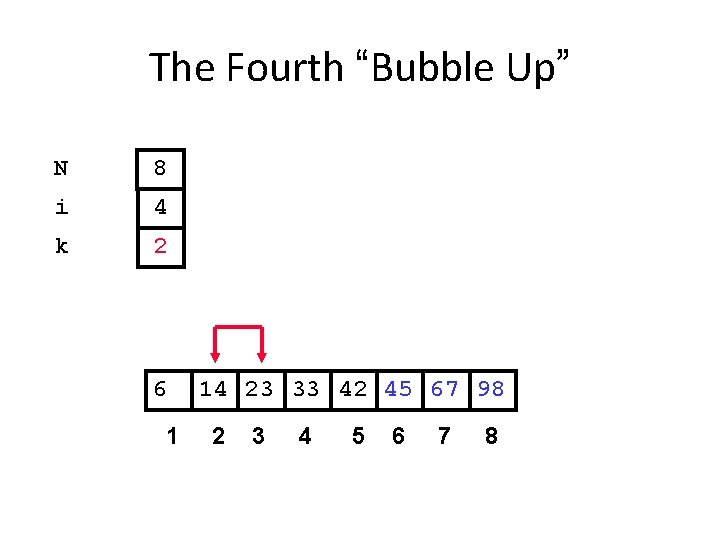
The Fourth “Bubble Up” N 8 i 4 k 2 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

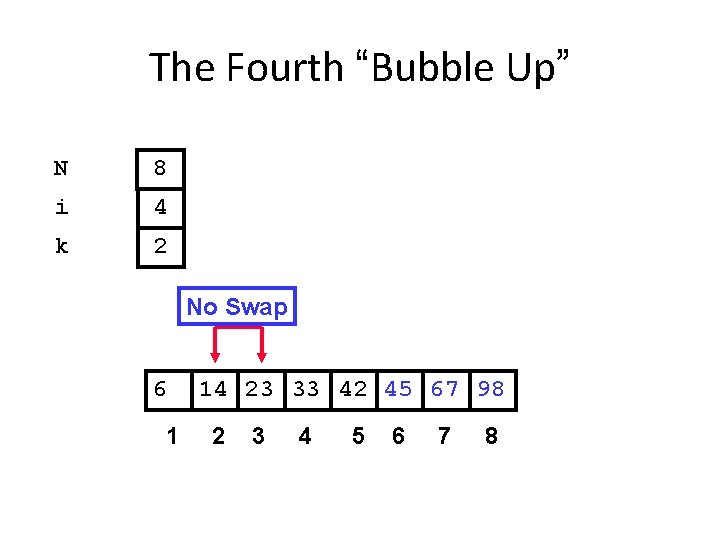
The Fourth “Bubble Up” N 8 i 4 k 2 No Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

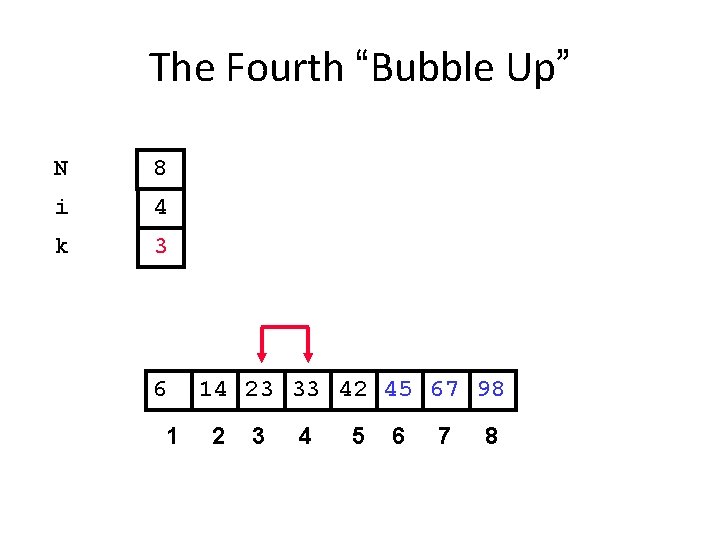
The Fourth “Bubble Up” N 8 i 4 k 3 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

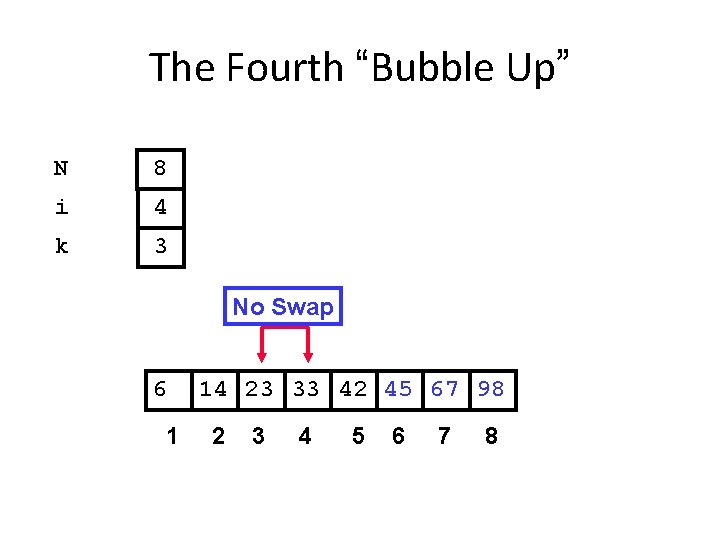
The Fourth “Bubble Up” N 8 i 4 k 3 No Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

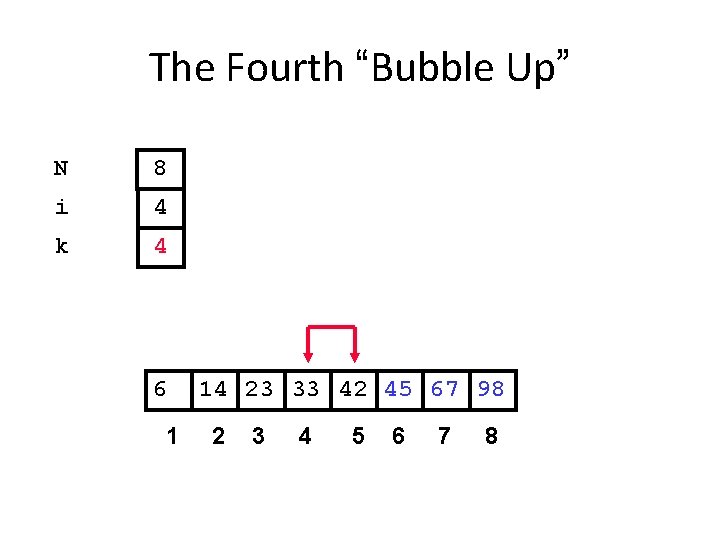
The Fourth “Bubble Up” N 8 i 4 k 4 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

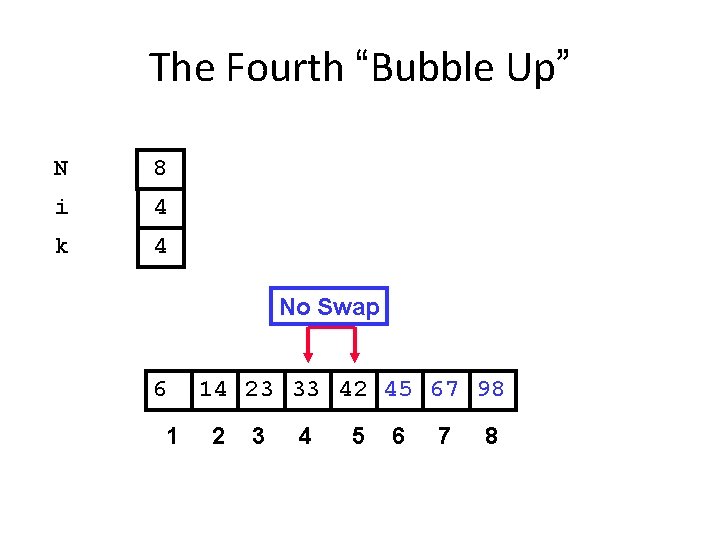
The Fourth “Bubble Up” N 8 i 4 k 4 No Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

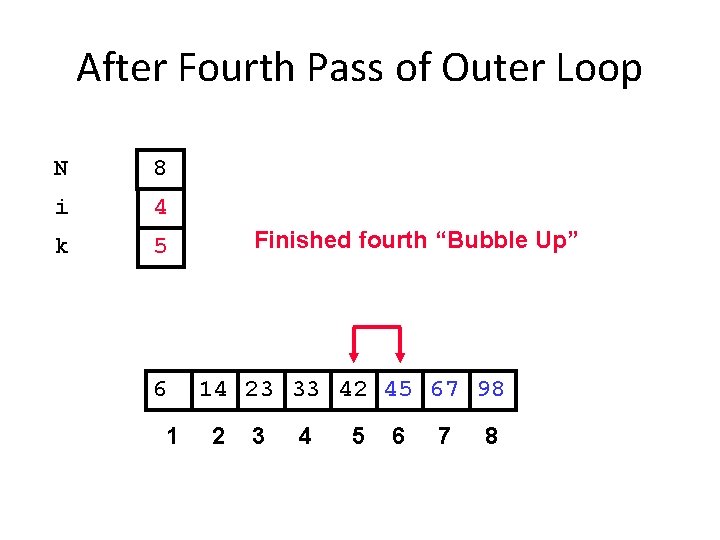
After Fourth Pass of Outer Loop N 8 i 4 k 5 6 1 Finished fourth “Bubble Up” 14 23 33 42 45 67 98 2 3 4 5 6 7 8

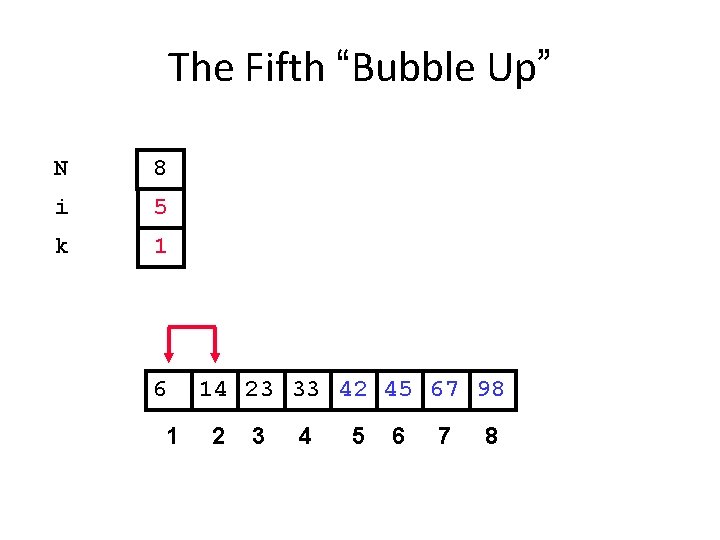
The Fifth “Bubble Up” N 8 i 5 k 1 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

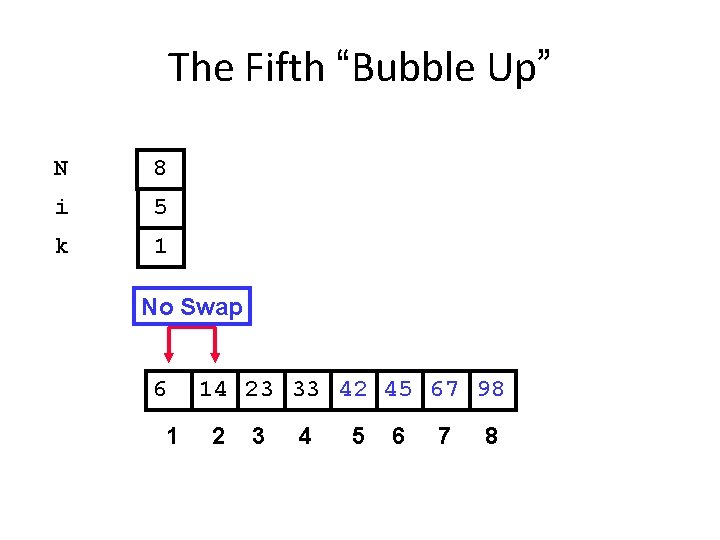
The Fifth “Bubble Up” N 8 i 5 k 1 No Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

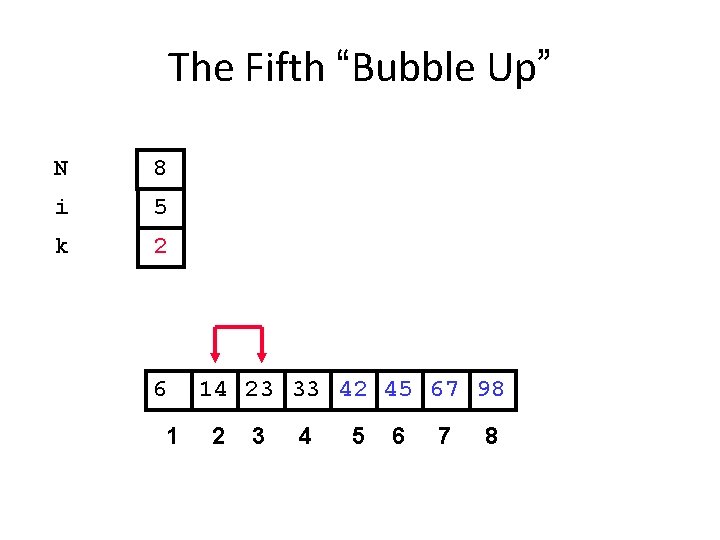
The Fifth “Bubble Up” N 8 i 5 k 2 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

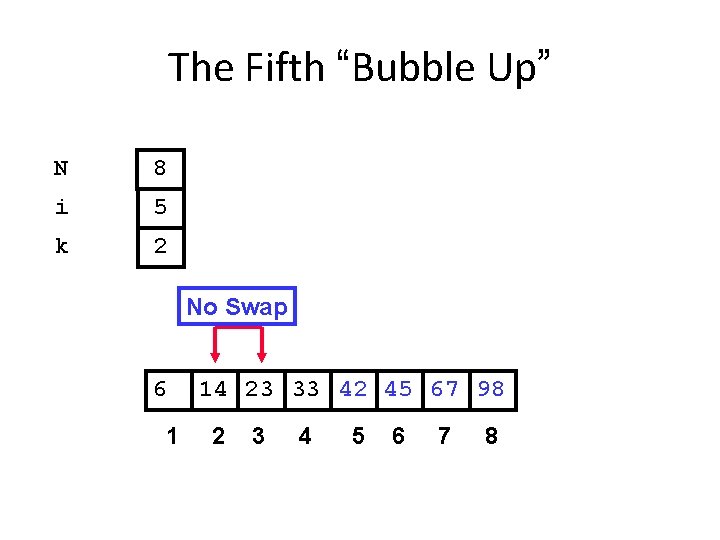
The Fifth “Bubble Up” N 8 i 5 k 2 No Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

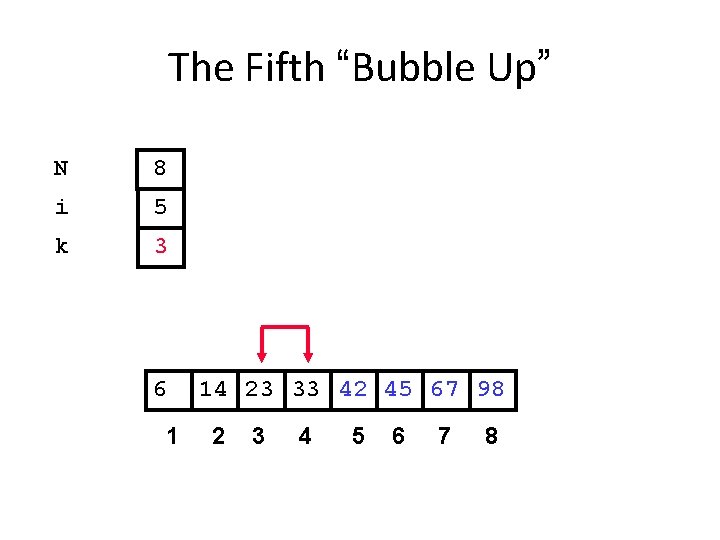
The Fifth “Bubble Up” N 8 i 5 k 3 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

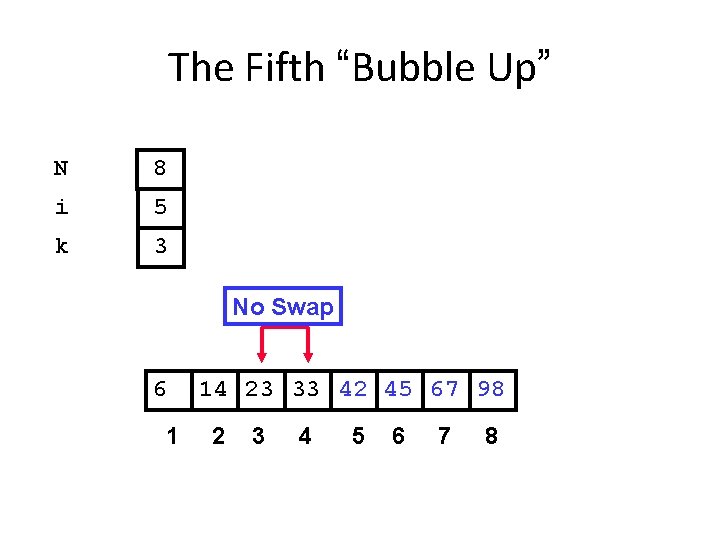
The Fifth “Bubble Up” N 8 i 5 k 3 No Swap 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

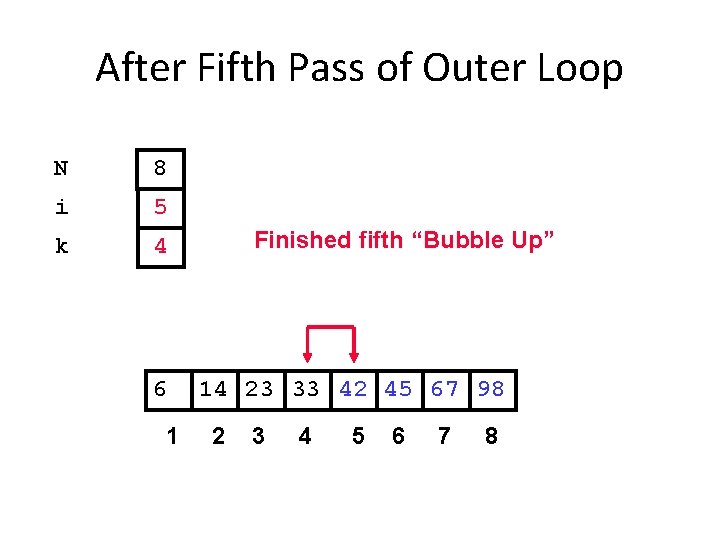
After Fifth Pass of Outer Loop N 8 i 5 k 4 6 1 Finished fifth “Bubble Up” 14 23 33 42 45 67 98 2 3 4 5 6 7 8

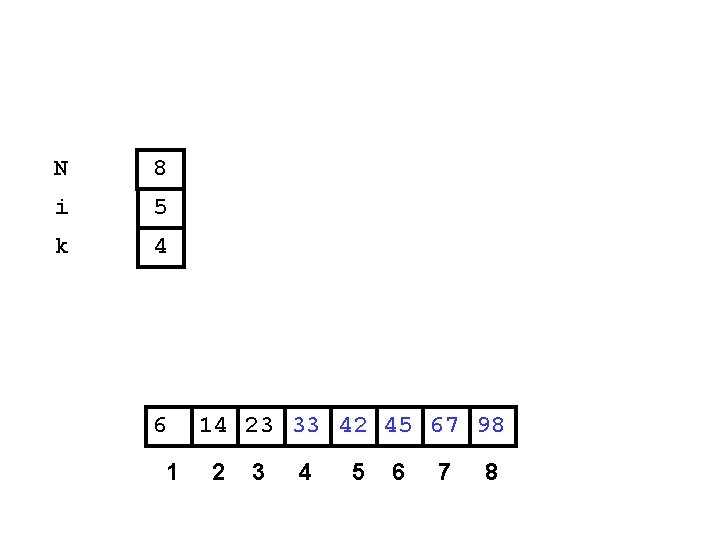
N 8 i 5 k 4 6 1 14 23 33 42 45 67 98 2 3 4 5 6 7 8

Summary • “Bubble Up” algorithm will move largest value to its correct location (to the right) • Repeat “Bubble Up” until all elements are correctly placed: – Maximum of N-1 times – Can finish early if no swapping occurs • We reduce the number of elements we compare each time one is correctly placed

Truth in CS Act • Bubble sort will do the job, but not efficiently • There are more efficient algorithms for sorting LB

Sorting Algorithms Courtesy of https: //www. youtube. com/watch? v=k. PRA 0 W 1 k. ECg